一种基于截断多项式的三角域V-系统构造

王相海, 刘乙萱, 曲思洁, 李 炜, 宋传鸣

(1.辽宁师范大学 计算机与信息技术学院,辽宁 大连 116029; 2.辽宁师范大学 数学学院,辽宁 大连 116029)

U-系统和V-系统[1-4]作为非连续正交函数，既可包含连续可微的多项式，也可以包含各阶导数出现间断的函数[5]，从而为有效的表示连续及非连续信号奠定了基础[6-7].作为V-系统的重要分支，尽管三角域上V-系统的构造要复杂一些，但其对于将频谱分析方法引入计算几何，实现几何对象的频谱分析和应用具有特殊的意义.自从文献[8]将V-系统推广到三角域上以来，人们对三角域上V-系统的构造和应用进行了研究.目前,该类型V-系统的构造主要通过两种方式实现，一种是基于生成元的构造方法[8]，另一种是通过构建线性无关函数组来实现[9-10]. 总体而言，三角域V-系统还处于发展阶段,有很多问题有待深入研究.本文提出一种基于截断多项式的三角域V-系统构造方法，依据三角域自相似剖分结构，从截断多项式和分片Legendre多项式出发，构造三角域V-系统的生成元，给出了所构造V-系统的解析表达式，同时对其性质进行了研究.

1 相关知识

V-系统是L2[0,1]空间上的一类正交完备函数系[8，11].k次V-系统是分组分类构造的，主要由基本函数和生成元两部分构成,包括k+1个尺度函数和k+1个小波函数.

定义1[11](V-系统生成元)区间[0,1]上函数集合fi(x),i=0,1,2,…,k，如果满足如下条件：

(1)fi(x)是以x=1/2为结点的分段k次多项式，且fi(x)在x=1/2处为Ci-1连续，约定C-1连续为间断;

(2)〈fi(x),fj(x)〉=δij,i,j∈{0，1,2,…,k},其中，

(3)〈fi(x),xj〉=0,i,j∈{0,1,2,…,k}.

fi(x),i=0,1,2,…,k,为区间[0,1]上的k次V-系统的生成元，也称为V-系统的小波函数.

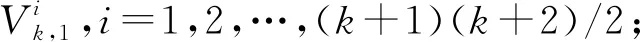
为了简化计算，本文选取以(0,0)(1,0)和(0,2)3点为顶点所围成的三角域(记为Δ)为V-系统的定义域，在Δ上定义函数内积为

(1)

对Δ作如图1所示的自相似的剖分：

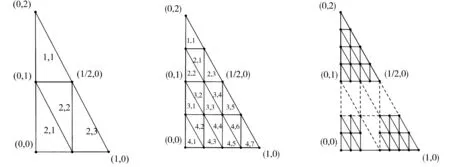
图1 三角域的自相似剖分及记号

定义2(截断多项式)引入记号(·)+=max{0,(·)}和(·)-=min{0,(·)}[4],定义截断多项式函数dm,n(x,y)为

(2)

容易证明函数dm,n(x,y)具有以下性质：

(1)dm,n(-x,y)=(-1)m+1dm,n(x,y)；

(2)dm,n(x,-y)=(-1)n+1dm,n(x,y)；

(3)dm,n(-x,-y)=(-1)m+n+2dm,n(x,y).

对于式(2),当x,y∈Δ时可以化简为

dm,n(x,y)=xmyn，m,n=0,1,2,….

(3)

2 基于截断多项式的三角域V-系统构造

2.1 构造方法

由Legendre多项式的Rodrigul公式[12]，定义三角域上(即x,y∈Δ)的二元Legendre多项式：

(4)

三角域上的k次V-系统按下列分组分类构造：

第一组：由定义在未做任何剖分三角域上的下列(k+1)(k+2)/2个基本函数构成：

dm,n(x,y)=xmyn，m+n=0,1,2,…,k.

(5)

按照内积(参见式(1))对其进行Gram-Schmidt规范正交化后作为基本函数，其下角标的排列按如下原则：①角标和(即m+n)递增;②在角标和相等的情况下，第一个角标即m递减.

第二组：在1级剖分下的3(k+1)(k+2)/2个生成元按照定义通过二元Legendre多项式生成，其下角标的排列也满足上述两原则.

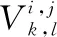
(6)

(7)

其中，l=3,4,5,…,α=1,2,3,…，2l-2,β=1,2,3,…,α,l=3,4,5,i=1,2,…,(k+1)(k+2)/2.

2.2 1次V-系统的构造

下面以k=1说明上述三角域V-系统的构造过程.

第一组基本函数:通过对dm,n(x,y)=xmyn,(m,n=0,1)规范正交化获得:

(8)

第二组生成元：通过对分片的二元Legendre多项式规范正交化获得：

(1)分片的二元Legendre多项式

(2)规范正交化

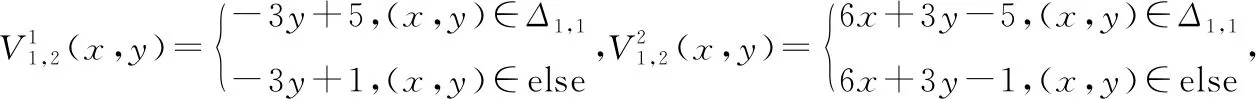
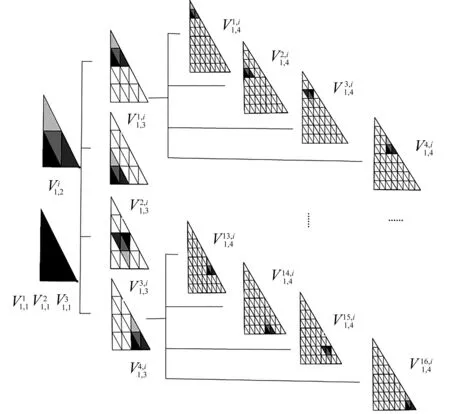
图2 1次V-系统基本函数与生成元之间的层次关系

3 所构造三角域V-系统的特性分析

定理1对于给定的非负整数k，所构建三角域k次V-系统的生成元必存在.

在生成元定义的三个条件中，条件(2)和条件(3)可以通过Gram-Schmidt正交化单位化满足.故只需证明存在以Δ的1级分割线为分线段的分片二元k次多项式fi(x,y),i=0,1,2,…,3(k+1)(k+2)/2,即存在上述分片二元k次多项式使其构造以函数在三角域Δ的1级分割线lj,j=1,2,3(参见图3)上的Ci(i=1,2,…,k)连续为依据.

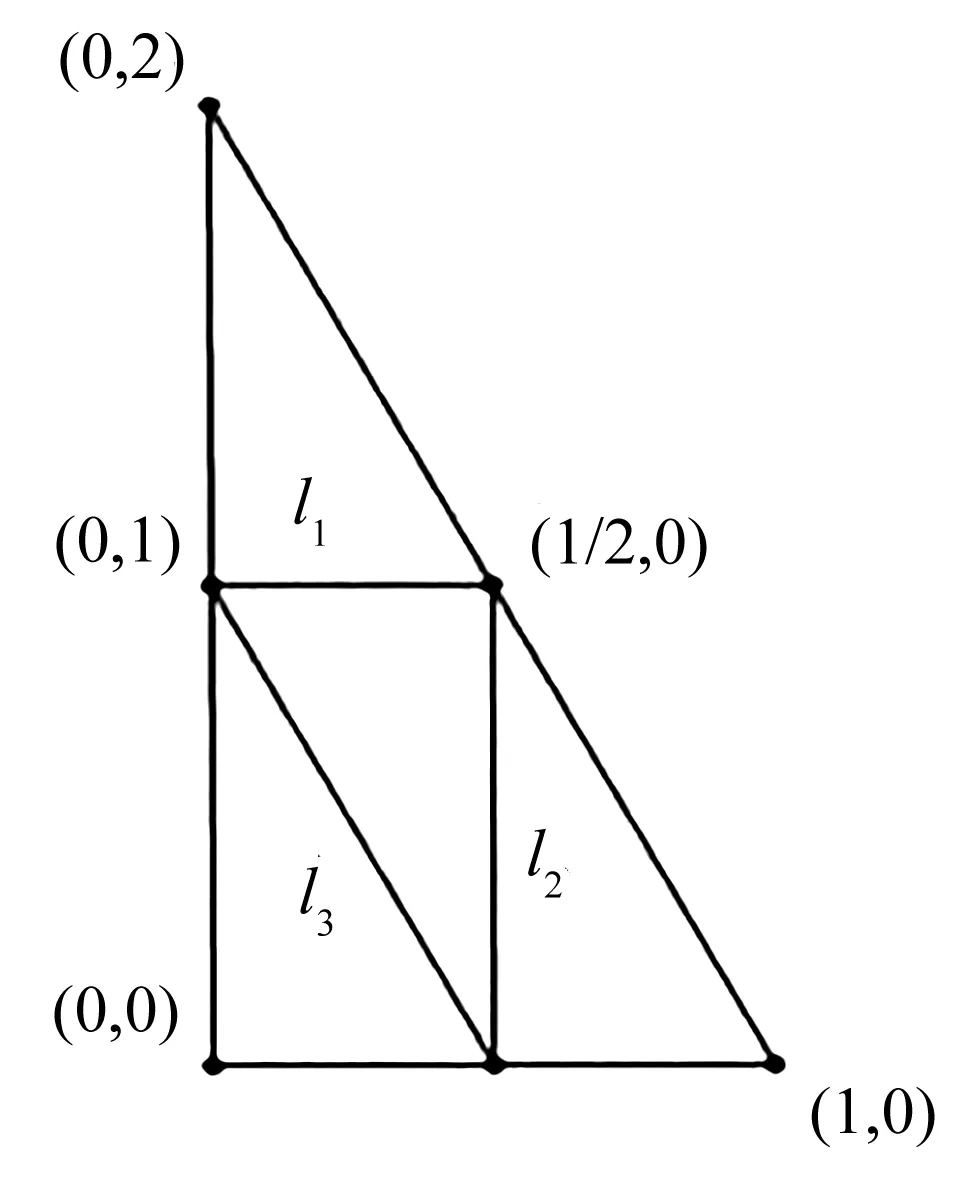
图3 三角域的1级分割线

事实上，二元Legendre多项式Pn,m(x,y)(见式(4))，当m+n=k时，按照前面标记法中下角标满足的条件，可以得到(k+1)(k+2)/2个不同的函数，为满足以1级分线作为分线段的二元函数，可令其在Δ1，1,Δ2，1,Δ2，3中某一个子三角域上为Pn,m(x,y),其余子三角域上为0,记为f(x,y),其个数为3×(k+1)(k+2)/2,所以对于给定的非负整数k，三角域上的k次V-系统的生成元必存在.

定理2所构造的k次V-系统是三角域上的规范正交的函数系.

其中,〈g,g〉为内积(参见式(1)).

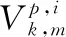
(9)

(10)

分以下几种情况讨论：

(1)当m=n,p=q,i=j时，即对于同一组同一类的任意两个相同的函数，此时有：

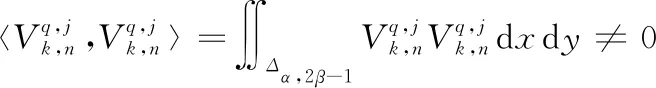
(2)当m=n,p=q,i≠j，即对于同一组同一类的任意两个不同的函数，此时有：

(3)当m=n,p≠q，即对于同一组不同类的任意两个不同的函数，此时有：

(4)当m≠n,即在不同组的任意两个不同的函数,此时有：

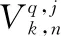
定理3若函数f(x,y)是定义在三角域上的以剖分线为分线段的分片k次多项式，则f(x,y)可以由三角域上的k次V-系统的有限项精确表达.

证对于任意正整数n，则定义在Δ的n级三角剖分域上的全体二元k次分片多项式组成4n×(k+1)(k+2)/2维线性空间.而k次V系统前n+1组函数总数为

由定理2知k次V-系统前n+1组函数可以成为线性空间的一组基底.

又因为函数f(x,y)是定义在三角域上的以剖分线为分线段的分片的k次多项式,故其可由k次V-系统前n+1组函数线性表出，即f(x,y)可以由k次V-系统中有限项函数的线性组合精确表达.

定理4三角域Δ上的k次V-系统具有多分辨性.

证设

则有

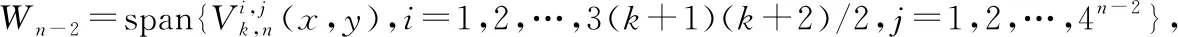
令Vj+1=Vj⊕Wj,则有

综上及k次V-系统的构造过程使得三角域Δ上的k次V系统满足多分辨分析的条件，从而使得所构造的三角域Δ上的k次V-统具有多分辨性.

4 结束语

本文在已有理论的基础上构造了一种基于截断多项式的三角域k次V-系统，从截断多项式和分片的二元的Legendre多项式出发构造三角域V-系统的生成元,且以三角域上的1次V-系统为例对具体过程进行了说明，同时对三角域V-系统生成元的存在性、规范正交性、再生性和多分辨性进行了论证.