随机干扰的变风量空调模糊迭代学习预测控制

张 淬，郭迎清，黄典贵

（1.黄冈师范学院机电与汽车学院，湖北 黄冈438000；2.西北工业大学动力与能源学院 陕西 西安710072；3.上海理工大学能源与动力工程学院 上海200093）

1 引言

变风量空调相对于传统的定风量空调来说具备低能高效的优势而得到了广泛的应用[1]。对于空调来说，节能始终是最受关注的一个问题，对于空调所在的环境来说，温度与湿度干扰是不可避免的。为跟踪给定信号，空调控制系统若在干扰条件下反应剧烈，将会导致较大的能耗损失，而且控制性能也会受到较大影响[2]。

迭代学习控制算法由于其被控对象模型精度要求较低而被学者广泛应用于轨迹跟踪控制[3]。近几年，迭代学习控制与其他理论相结合产生了许多的新型迭代学习控制方法比如PID迭代学习控制，自适应迭代学习控制以及模型参考迭代学习控制等[4-5]。但是迭代学习控制的应用必须满足一个严格的重复性条件，但是在实际的变风量空调运行中，遇到的干扰基本上都是随机干扰，因此传统的迭代学习控制无法实现随机干扰条件下的空调温湿度跟踪控制。

传统的迭代学习预测控制通过求解稳定条件确定迭代学习速率以及预测步长，但是此种方法使得该种控制器具备一定的保守性[6]。针对变风量空调的跟踪控制以及能耗节约，提出了一种二维框架理论的模糊迭代学习预测控制。首先利用二维跟踪框架对变风量空调模型进行相应处理从而得到相应的二维模型，另外，为了降低传统迭代学习预测控制的保守性，利用模糊理论对学习速率与预测步长进行在线自适应调整，使得该控制器在保证跟踪精度的条件下，提升响应速度以及干扰鲁棒性，降低了扰动条件下的能耗损失。

2 变风量空调建模

严格来说变风量空调系统是一种典型的非线性系统，为便于控制器设计，本文根据其工作原理进行线性化建模，该系统主要由两部分组成，第一部分是空调所在空间模型，根据文献[7]可知所在空间温湿度模型分别为：

式中：tn—房间温度，ts—送风温度，T1r—所在空间温度的时间常数，K1r—空间温度的放大系数。所在空间的湿度模型为：dn—空间湿度，ds—送风湿度，T2r—空间湿度的时间常数。

第二部分是空调表冷器模型，表冷器的作用主要是，利用盘管内的冷冻水降低盘管表面流过的空气的湿度和温度。

其相应温度与湿度模型为：

式中：T1h,T1c,T2c—各自模型的时间长数，K1h,K1c,K2c—各自模型的放大系数。

当送风与室内空气混合时只能改变室内空气的温度，不会改变室内空气的含湿量。

所以该变风量空调系统的传递函数为：

3 二维框架理论

变风量空调在相同季节每天基本上均进行着重复工作，此种工作特点与间歇过程的特点十分相似，均是在有限的运性时间内不断的重复相同的工作。所以，我们将变风量空调的控制作为一个间歇过程，另外还将变风量空调的温湿度控制问题转化成相应的间歇过程轨迹跟踪问题。假设变风量空调系统的离散状态空间方程如下：

式中：k—运行批次，t—运行时刻，且满足t∈[1,N]，N代表间歇过程一个批次的采样次数，x∈Rn—状态变量，u∈Rn—控制量，d∈Rn—干扰输入，A,B,C—系统矩阵。

根据间歇过程的特点：不断地在固定有限时间上重复某一确定工作，则可将间歇过程看成有时间轴和批次轴组成的二维系统，从而便于对间歇过程轨迹跟踪问题的研究。存在如下二维状态变量模型：

进一步将轨迹跟踪问题转换为：寻找Δu(t-1,k)，使得e(t,k+1)满足收敛条件。

为便于说明二维框架理论，假设存在一个二维状态空间模型：

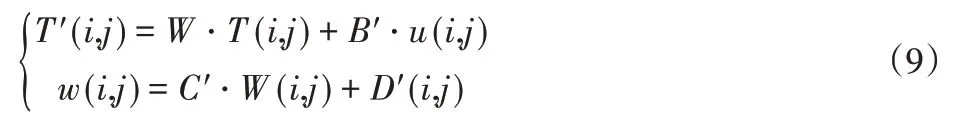
其中：T(i,j)=[R(i,j)S(i,j)]T，

其中大小关系的定义为当h≤i且k≤j时，(h,k)≤(i,j)，当且仅当h=i且k=j时，(h,k)=(i,j)。

引理1[8]：设R(i,0)和S(i,0)为相应的初始值，若在(i,j)满足(i,j)≠(0,0)的条件下有u(i,j)=0成立，那么可得T(i,j)=Wi,jT(0,0)。

利用上述分析对二维系统的零状态响应进行求解：对于任意的(h,k)＜(i,j)，

若满足单独输入u(h,k)≠0且R(i,0)与S(i,0)均等于0，

那么存在如下关系式：

根据线性系统理论可知状态转移矩阵与(i,j)无关，所以T(h,k)对T(i,j)的影响可以等价于Wi-h,j-kT(h,k)。

所以二维系统的零状态响应可以表示为：

进一步求解二维系统的零输入响应，若R(0,k)不等于0，而S(h,0)等于0，此时系统输入为0，

故存在如下关系式：

此时零输入响应为：

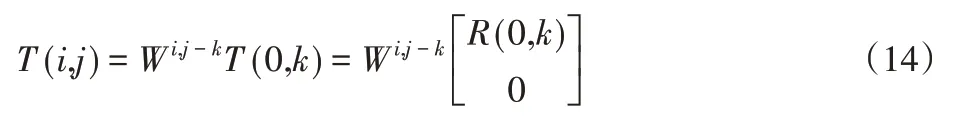
同理，若R(0,k)为0，而S(h,0)不等于0，此时系统输入为0，故存在如下关系式：

此时零输入响应为：

综合上述推理可知该二维系统的零输出响应为：

4 模糊迭代学习预测控制

4.1 迭代学习预测控制

引理2[9]：若系统的初始值保持不变，则二维模型满足η(1,k)=0,∀k＞0

针对二维系统，设计如下形式的迭代学习控制器：

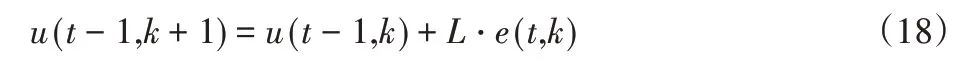
式中：L—迭代学习速率。

将该种类型迭代学习控制的控制量作为二维系统的输入量可得到式（19）：

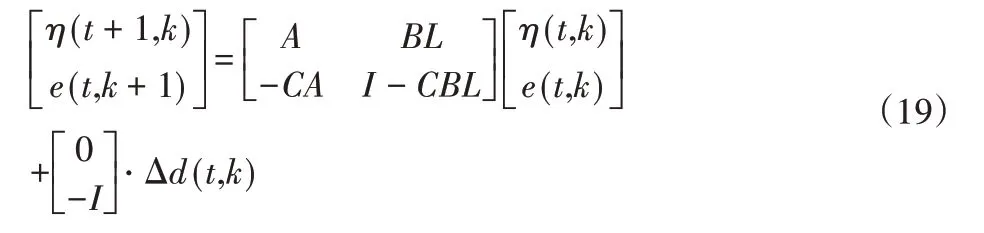
根据引理2可知式（20）等价于：

在满足假设的情况下针对公式（18）所示的控制器，迭代学习控制收敛的充分条件为是W0,1能够保证渐近稳定，该条件等价于矩阵I-CBL的特征值包含在单位圆里面[10]。

若上述充分条件成立，则只需寻找到合适矩阵L就等同于完成迭代学习控制器的设计。

已知存在如下结论：针对线性时不变系统来说，能够通过压缩映射方法对P型迭代学习控制的收敛性进行分析，相当于在系统满足全局Lipschitz条件和初始条件相同的情况下，若，所以该迭代学习控制算法单调收敛。

根据上述结论，本文结合二维框架理论，提出一种针对随机扰动的迭代学习预测控制方法，其表达式为：

式中：Δ(t-1,k+1)—批次间的控制量，

(t-1,k+1)—批次内的控制量，该批次内控制量主要是为了使得系统在运行过程中对随机性、非重复性干扰具有鲁棒性。

批次间通过P型迭代学习控制律进行控制可得相应的控制量表达式为：

式中迭代学习速率L可以通过迭代学习控制的收敛条件求得。

根据二维框架理论可知在迭代预测控制算法的作用下，二维系统的响应为：

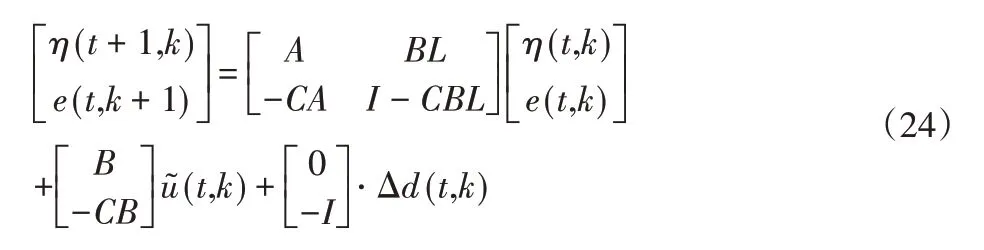
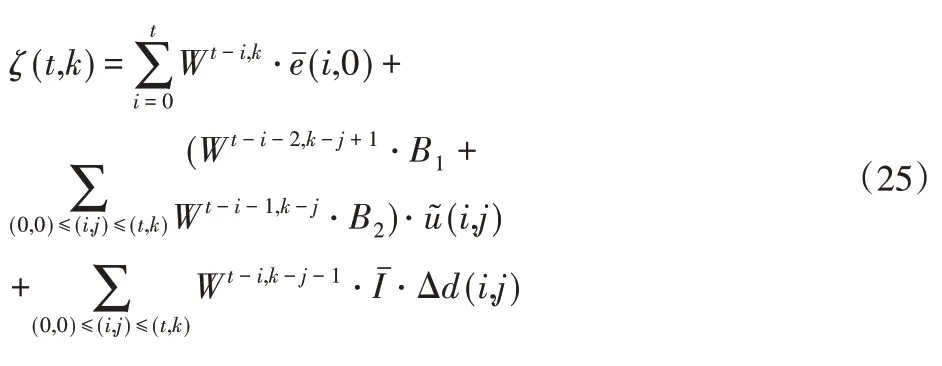
利用式（25）得到相应的预测模型为：

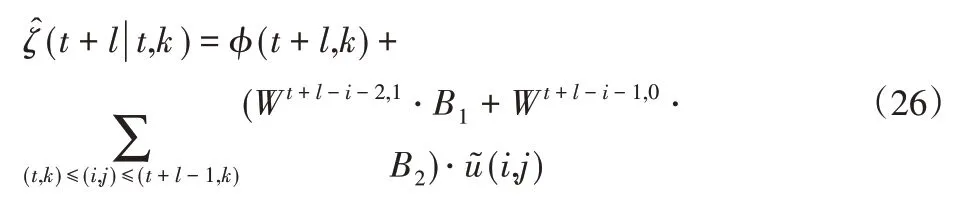
式中：l∈[1,m]，m代表的是预测步长。

φ(t+l,k)预测初始值能够通过之前时刻的状态求得：

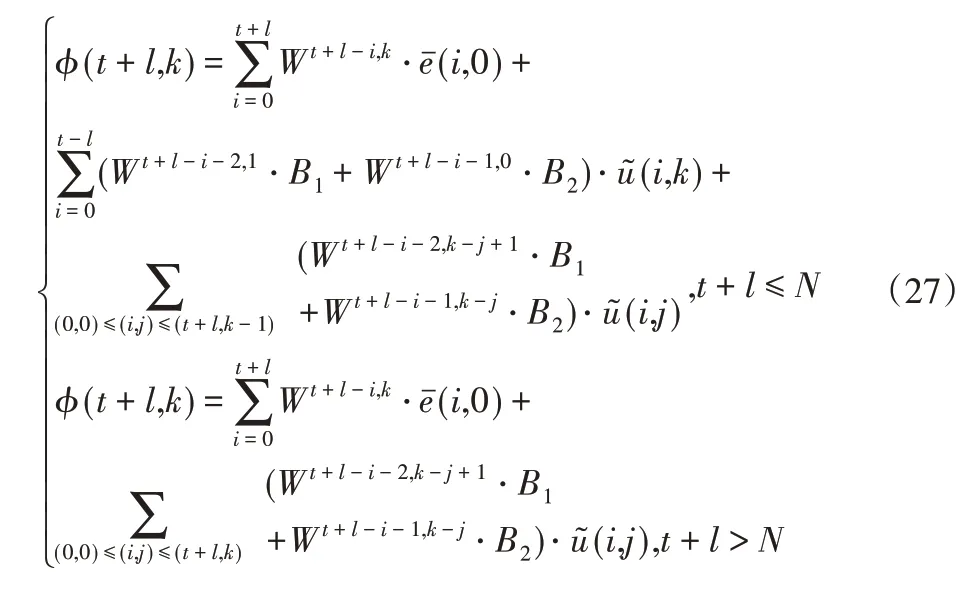
定义矩阵：

则公式（28）等价于：

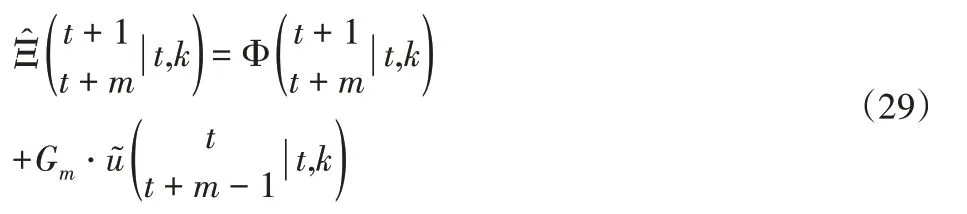
其中的α,β,γ均为相应权重系数，且满足均不小于0的条件。进一步将该目标函数表达式（30）转换为矩阵形式：

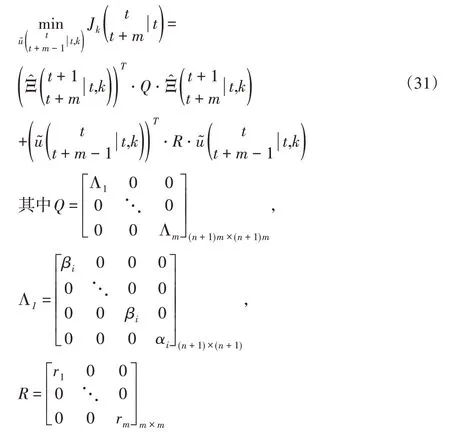
利用无约束条件下的优化理论进行求解可得相应的解的表达式为：

根据预测控制理论可知在控制系统运行过程中，是将当前时刻的控制输入作用于被控对象，所以某一时刻的控制量为：

4.2 模糊调整策略

迭代学习预测控制的控制效果很大程度上依赖于学习速率与预测步长的大小。为达到较好的控制效果，学习速率与预测步长应该随状态的变化而自适应的调整。

因此，考虑到模糊理论较强的自适应调整能力[11]，提出了一种基于模糊规则的变学习速率与预测步长的迭代学习预测控制器。

模糊控制器的输入量为控制响应与给定信号的误差e(k)和及其变化量Δe(k)，其中Δe(k)=e(k+1)-e(k)，这两个输入量能够反映此时预测控制的准确性以及鲁棒性。

当预测误差以及误差变化率较大时，选择较小的预测步长以及较大的学习速率从而提高预测控制精度，当误差较小时，选择较大预测步长以及较小的学习速率提升鲁棒性以及响应速度，输出量为学习速率l以及预测步长m，模糊输入量与输出量语言的模糊集分别为：{PB,PM,PS,ZR,NS,NM,NB},{B,MB,M,MS,S},分别进行归一化处理，得到输入量与输出量的论域子集为：

式中：学习速率l的取值必须从稳定范围内选择。

控制器输入和输出的隶属函数曲线，如图1和图2所示。

图1 输入隶属度函数Fig.1 Input Membership Function

图2 输出输出隶属度函数Fig.2 Output Membership Function

模糊控制规则，如表1所示。

表1 模糊规则表Tab.1 Fuzzy Rules Table

5 仿真验证

已知变风量空调的模型如式（6）所示，从该模型中可以发现湿度控制是一个单独的控制回路，为了便于验证，将式（6）所示的变风量湿度控制传递函数模型为研究对象：

定义采样周期为T=0.5，将连续传递函数（36）离散化得到离散状态空间模型为：

利用MATLAB进行仿真，仿真验证主要通过迭代次数均为10次的P型迭代学习控制控制、二维迭代学习预测控制以及二维模糊迭代学习预测控制三种控制算法进行对比。

给定一个湿度值为0.8的定常信号，在无噪声干扰条件下，分别通过上述三种控制方式进行控制，响应对比图，如图3所示。

图3 无扰动跟踪响应图Fig.3 Disturbance-Free Tracking Response Diagram

从图3中可以看出，P型迭代学习控制的响应速度最快，其调节时间仅为16.7s，而二维迭代学习预测控制与二维模糊迭代学习预测控制的调节时间分别为24.5s和21.1s，说明迭代学习控制响应速度最快，但是模糊调整策略有助于提升迭代预测控制的响应速度。且通过图4所示的稳态放大图可知两种迭代学习预测控制方法在稳态时均有不同程度的振荡，相较而言，模糊迭代学习预测控制的稳态过程比较平稳，与目标湿度值也更为接近。这说明P型迭代学习控制在无干扰条件下的跟踪控制响应速度更快，稳态性能更好。而迭代学习预测控制相较于迭代学习预测控制响应速度较慢，稳态误差较大，主要原因是加入预测环节考虑了目标特性与动态特性。虽然两种迭代控制效果均不如P型迭代学习控制，但是依旧能够保证一定的控制性能，模糊迭代学习预测控制的稳态误差小于固定学习速率与步长迭代学习预测控制，说明模糊调整策略能够减小跟踪稳态误差。进一步在湿度值为0.8的定常信号条件下，给定一个周期性的扰动信号：，在该扰动信号条件下三个控制算法的控制响应，如图5所示，定义摆动量为响应超过目标值后的最大值减去最小值。在该种正弦周期性干扰下三种控制响应的摆动量大小，如表2所示。

图4 跟踪响应放大图Fig.4 Tracking Response Magnification

图5 周期扰动下的跟踪响应图Fig.5 Tracking Response Diagram under Periodic Perturbation

表2 响应最大摆动量对比表Tab.2 Contrast Ttable of Maximum Oscillation Response

从图5和表2中可以得出，正弦干扰信号对P型迭代学习控制的影响最大，而相对来说，该周期性干扰对两种迭代预测控制算法的影响较小，进一步验证了无论是固定参数还是模糊策略的迭代学习预测控制对于周期性扰动均具有较好的鲁棒性。

考虑到实际空调运行过程中的空气流动具有混沌特性，为模拟该混沌扰动，在同样目标湿度值的条件下，给定一个随机噪声干扰，该噪声干扰的湿度幅值振荡为±0.5，该噪声干扰图，如图6所示。

图6 随机扰动信号图Fig.6 Random Disturbance Signal Graph

在此种条件下，三个控制器的响应曲线与稳态误差对比放大图如图7与图8所示，响应的摆动量，如表3所示。从中明显可以看出，P型迭代学习控制与二维迭代学习预测控制的响应由于噪声影响过大，较为明显的偏离目标湿度值，无法实现对目标的跟踪，说明P型迭代学习控制与传统迭代学习预测控制对随机干扰的鲁棒性能较差，无法保证较大随机干扰条件下的跟踪性能。而二维模糊迭代学习预测控制响应依旧保持着较好的响应速度，且在达到稳态后的摆动量仅为P型迭代学习控制与二维迭代学习预测控制的11.35%和15.64%，响应曲线也显示了该控制响应依旧能够较好的跟踪目标湿度值。说明加入了预测控制之后，该控制器对随机扰动具有较好的鲁棒性，能够在随机噪声影响下保证较好的跟踪能力。

图7 随机扰动下的跟踪响应Fig.7 Tracking Response under Random Perturbation

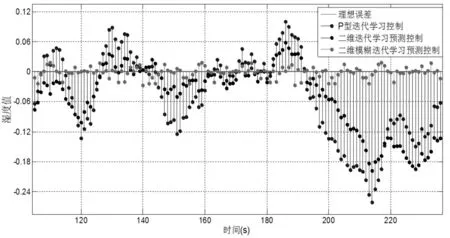
图8 稳态误差放大对比图Fig.8 Steady-State Error Amplification Contrast Diagram

表3 响应最大摆动量对比表Tab.3 Contrast Table of Maximum Oscillation Response

6 结语

针对变风量空调系统设计了一种基于二维框架理论的模糊迭代学习预测控制器。首先建立了变风量空调系统的状态空间模型，然后介绍了二维框架理论，进一步利用该理论得到了迭代学习控制收敛的条件，最后得到了二维模糊迭代学习预测控制器的设计方法。经过仿真对比得到如下结论：1、P型迭代学习控制相对于迭代学习预测控制，更适合无干扰条件下精确模型的跟踪控制。2、二维迭代学习预测控制对于周期性干扰具备较好的鲁棒性，但对随机干扰的鲁棒性较差，无法在随即干扰的条件下实现较好的跟踪。3、二维模糊迭代学习预测控制不仅能够保证在无干扰或者周期性干扰条件下具备较好的跟踪效果，而且对大随机干扰具有较强的鲁棒性，能够保证在较强随机干扰下的良好跟踪能力。