分块自适应加权改进大规模模糊聚类

田彦彦，孙 静,2

（1.郑州工业应用技术学院机电工程学院，河南 郑州451100；2.吉林大学软件学院，吉林 长春130000；）

1 引言

随着计算机技术的发展，数据的大规模增长和信息系统的云服务化成为基础应用，海量化、多样化和复杂化成为数据处理的常态，如何从这些数据中提取有用信息，逐渐被人们所重视，聚类可以从各种无标记数据中通过一定的判断策略发现数据的内在关联而实现无监督聚类，对分析或挖掘热点话题等信息具有重要的作用，已在计算机视觉、数据挖掘、审计评定、云计算、自动化控制以及网络安全等学科领域具有众多的应用，也是近几年数据处理领域研究的重点［1］。

模糊聚类［2］基于模糊集理论分析数据集中数据对各个聚类中心的模糊隶属度，基于模糊集理论可以实现更准确的聚类分析，多视角聚类［3］通常以传统聚类方法为基础，将其目标函数扩展为多视角，并对扩展后的目标函数添加约束以平衡视角一致性和聚类贡献的差异性。为此，文献［4］联合视角内划分与视角间协同的学习机制，提出多代表点一致的多视角模糊聚类算法，并通过拉格朗日乘子和KKT条件进行目标函数优化；文献［5］基于稀疏相似和最大熵提出两级变权的多视角自适应聚类算法；文献［6］联合NMF协同提高多视角聚类的相似矩阵计算，以独立准则共享视角信息，从而优化冗余共享提高算法聚类性能。

分布式计算有效提高了大规模数据集聚类的处理效率，但其节点间的数据通讯占用了额外的资源，为解决节点通讯对资源的占用，文中提出基于大数据集抽样分块的多视角自适应模糊聚类算法，算法在改进多视角模糊聚类基础上，通过数据抽样分块和自适应加权块内聚类实现大规模数据集聚类。实验结果验证了算法的有效性。

2 模糊聚类算法的原理

设规模为N的待聚类数据集为X={x1,x2,…,xN}N×D，D为数据集中数据的维数，N≫D，设V={v1,v2,…,vC}C×D为C类聚类中心，对象x（nn=1,2,…,N）划分为第c=1,2,…,C类聚类中心的隶属度记为为模糊划分矩阵，则基于C均值的模糊聚类算法FCM（Fuzzy C-means）的聚类目标函数可以表示为：

使式（1）所示目标函数取得局部极小值则可以得到数据集的模糊划分矩阵U=[ui,j]，其迭代优化计算式分别为：

式中：m—模糊指数，针对经典FCM算法的unc无法精确表达数据集的分类信息问题，文献将中立与拒分两种度量策略引入到FCM算法中，改进后的正则化模型［7］，可描述为

式中：η=[ηij]、ε=[εij]—聚类算法的模糊中立度矩阵与模糊拒分度矩阵，其相应的约束条件为∑uij( 2-εik)=1和∑(ηij+εik/c)=1，采用拉格朗日乘子法可以根据式（4）计算相关参数。为提高式（4）改进模型的鲁棒性，将文献［10］中的邻域正则约束引入式（4），提出具有抗噪优化的鲁棒模糊聚类方法，其改进后的目标函数为：

式中：f(xi,vi)—描述了领域空间信息约束特征，主要用于提高算法的鲁棒性并抵制背景噪声影响，其计算式为：

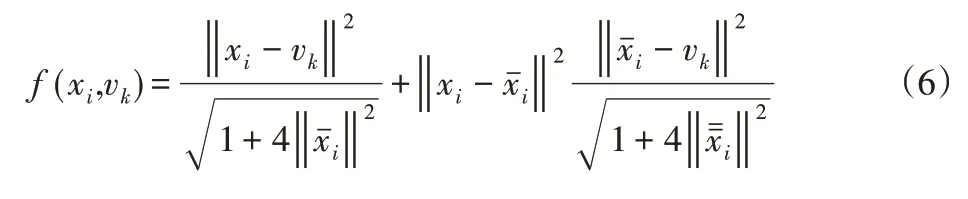
为提高聚类算法对多样化数据的适应性，通过低秩约束和熵加权对改进后的自适应鲁棒模糊聚类算法进行多视角扩展，通过视角系数优化算法在迭代过程中对可分离性视角的权重分配，从而提高算法对多样化数据的聚类性能，低秩约束有利于改进算法在聚类过程中的多视角一致性，而熵加权则有利于保持不同视角数据之间的聚类贡献差异性。

高频接触振动产生巨大的垂直力增量，使钢轨塑变层遭受反复和快速的锤击作用，逐渐在钢轨表面形成明暗相间的波浪形磨耗。当有切向力作用的动轮经过其上时，瞬间的局部接触间断可使动轮积聚起很大的能量，一旦在波浪形的峰部恢复接触时，聚合的能量就骤然被释放出来。

令多视角数据的各视角系数为wk≥0，则有，则扩展算法的熵加权正则项为：

而低秩约束可以将多视角约束为核范数最小化求解问题，即Γ(U)=‖U‖，U－多视角隶属度组成的矩阵，这样基于低迭约束和熵加权的改进算法的目标函数可以表示为：

式中：N—数据量，C—聚类中心数，θ、λ—正则化因子。对于式（9）的迭代求解，通过固定其中的w和U，同时迭代更新聚类中心矩阵V，可得第t+1次迭代计算得到的聚类中心的解为：

而通过固定式（9）中的w和Z，同时迭代更新模糊隶属度，可得第t+1次迭代计算得到的模糊隶属度U(t)+1为：

式（9）所示改进模型以等价关系融合了多视角聚类与模糊聚类的优势，具有全局最优解［9］，但算法巨大的计算量使其在应用于大规模数据聚类时无法获得最优聚类甚至无法得到聚类结果，为此，借鉴已有的大规模数据分块思想，对提出的多视角自适应模糊聚类算法进行改进，以适于越来越普遍的大数据处理场景。

3 分块加权大规模模糊聚类

大规模数据集难以一次性全部读入内存中，因而给聚类算法的数据读取带来压力，Canopy算法根据一定的数据预处理规则可以将原始大规模数据集划分为多个数据片，每个数据包含一定数量的数据，因此可以通过Canopy算法先对数据进行分块预处理，将原始大规模数据集划分为可同读入内存进行处理的小规模数据片，同时Canopy算法可以根据数据特征初步获得数据的粗糙聚类中心，从而进一步减少后续数据处理过程的迭代次数，提高算法收敛效率。

对于原始数据集list=X={x1,x2,…,xN}N×D，预设两个阈值T1和T2，T1＞T2，则判断任意一个数据点P与list中剩余数据的距离值d，并将T1＜d＜T1的原始数据点作为候选的初始聚类中心，重复执行，直接所有数据被判断一遍，同时将d＜T1的数据合并为一个临时数据片。

在获得初始聚类中心及其相应聚类后，对每个聚类中的数据进行随机抽样，并将一次抽样结果作为一个数据分块，根据数据规模判断分块数及每个数据块的规模，并对数据块进行编号。然后对第一个数据块执行第2节所示的多视角自适应模型聚类算法，获得第一个数据块的聚类结果及其聚类的质心，由于每个聚类的质心最具有该类的代表性，因而将该质心作为代表点合并到第二个数据块中，并参与第二个数据块的聚类，依次类推，直接所有数据块均完成多视角自适应模糊聚类，从而获得最终大规模数据集模糊聚类结果。

由于从第二个数据块开始，其中的数据除了原始抽样数据外，还新加入了上一数据块的代表点数据，从数据对最终聚类结果的贡献看，由上一数据块传递来的代表点对于当前块最终的聚类具有更大的贡献，因而从第二个数据块开始，需要对原始抽样数据和代表点数据赋值不同的权重，以描述其对最终聚类结果的贡献，且随着数据块序号的增加，其新加入的代表点应自适应的赋值相应更大的权重，为此，文中对含有代表点的数据块的聚类，其目标函数中增加数据的自适应权重，修改后的目标函数为：

式中：wn＞0—数据权重，其描述了数据块不同属性数据的聚类贡献，对于不同序号的数据块，该权重值由前一数据块的权重值累积得到，即

表1 大规模分块多视角自适应FCM算法Tab.1 Large-Scale Split Field Multiview FCM Algorithm

4 实验与分析

为验证文中提出的分块多视角自适应模糊聚类算法（简记为pmvaFCM）的有效性，采用来自UCI机器学习库的Iris和Wine数据集［10］作为测试数据，以传统FCM算法［4］、多视角FCM算法（mvFCM）［9］作为比较算法，实验平台为：Intel i7 7700HQ@2.8G Hz，16G内存，NVIDIA GTX1060 6G显存，以matlab 2016a软件开发实验算法。

从两个数据集中随机选取105条记录进行实验测试，数据集中加入噪声，以多次实验结果的聚类准确度平均值作为聚类性能评价指标，首先测试不同算法的聚类性能效率实验结果，如表2所示和图1所示。

表2 不同算法的聚类性能比较Tab.2 Performance Comparison of Different Algorithms

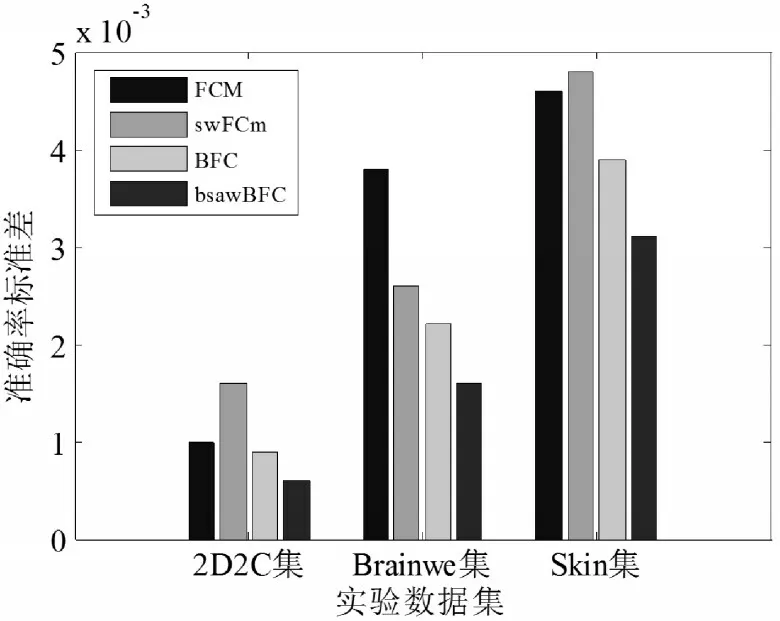
图1 各算法聚类准确率标准差Fig.1 Standard Deviation of Clustering Accuracy of Each Algorithm

从表2和表1实验结果可以看出，文中改进pmvaFCM算法的收敛迭代次数有了大幅减少，从而在相同硬件条件下有效减少算法的聚类时间，这主要是因为算法在将数据集分块后，大多数数据块仅有若干代表点等数据是的变量动，因而各数据块的聚类迭代时间变化不大，而通过合理设置数据分块大小，可以有效减少每个数据块的聚类迭代次数。另一方面，从平均聚类准确率实验结果可以看出，文中算法取得与mvFCM相似但略好的聚类准确率，这主要是因为，通过Canopy算法进行初始聚类中心提取后，后续的数据抽样分块及聚类初始聚类中心设置，都有了一个较为准确的参考，使得相关参数的设置更加合理，从而使得算法取得更优的识别准确率。从图1准确度标准差可以看出，文中算法在2个数据集中均取得最小的标准差，说明文中算法具有最优的聚类稳定性。

5 结论

为解决传统FCM模糊聚类算法在处理大规模数据集时遇到的时间复杂和内存不足等瓶颈，提出基于大数据集抽样分块的多视角自适应模糊聚类算法，算法通过邻域正则约束提高传统FDM算法的抗噪性，通过低秩与熵加权约束提高多视角一致性，以提高算法对多样化数据聚类的适应性，最后通过Canopy算法初始聚类中心提取和数据抽样分块优化算法对大规模数据聚类的适应性，实验结果验证算法的有效性。