新型集装箱板材上下料机械手动力学建模与仿真

王晓磊，王永钊，刘 祥

（辽宁工业大学机械工程与自动化学院，辽宁 锦州121001）

1 引言

在目前的集装箱生产过程中，集装箱角柱板材的折弯工序大多依然采用人工进行板材的上下料，既危险，生产效率也低，因此，本文提出了一种基于2-P（Pa）并联机构（其中，P表示直线运动副，Pa表示平行四边形结构）的集装箱角柱板材上下料机械手。相对于串联结构，并联结构具有结构简单、精度高、刚度大、积累误差小等优点，在搬运、产品分拣、机械加工、装配等自动化领域中得到了广泛的应用［1］，也越来越受到受到研究人员的关注［2-3］。在对少自由度并联机械手的研究中，建立动力学模型是对并联机构进行动力学分析的基础，也是实现并联机构高精度控制的前提［4］。常用的建立动力学方程的方法有：牛顿-欧拉法［5］、虚功原理［6］、凯恩方法［7］、拉格朗日法［8］等方法。相对于其他方法，拉格朗日法方程数目少，易于转化，便于对并联机构的控制。文献［9］基于拉格朗日第一类方程，建立了2自由度平面并联运动平台的操作空间动力学模型。并基于此分析了其各项运动学性能指标和动态性能指标。文献［10］基于拉格朗日法对一种2-DOF类球面并联转台进行了动力学建模和分析。

本文以基于2-P（Pa）并联结构的板材上下料机械手为研究对象，利用解析法求出了并联机构的位置正反解，末端执行机构的机构的速度方程与加速度方程。采用拉格朗日方程建立了机构的动力学模型，并通过理论计算与实例分析，验证了动力学模型的正确性与有效性。

2 集装箱角柱板材折弯工序介绍

集装箱角柱板材的胚料为长方形钢板，在其折弯工序中，需要沿其长边平行方向进行多次折弯。图1为角柱板材的折弯工艺步骤示意图，其中各图为不同阶段的板材横截面二维图。蓝色箭头所指处为折弯线。在工人手工进行上下料作业时，首先由两人同时抓取钢板，抬至折弯机置料台卡位处，进行如图1（a）所示的两次折弯，然后两人将板材抬下，进行180度翻转后，再将板材抬上折弯机置料台卡位处，进行如图1（b）和（c）所示的三次折弯。折弯结束后，两人将板材抬至成品堆垛区板材最终成品，如图2所示。

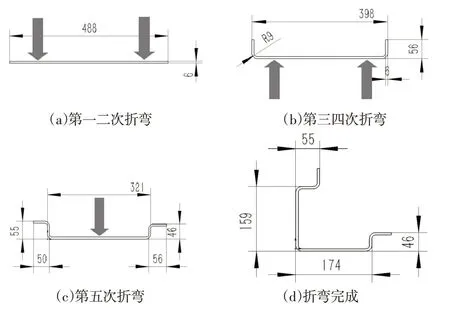
图1 折弯工艺步骤示意图Fig.1 Bending Process Steps

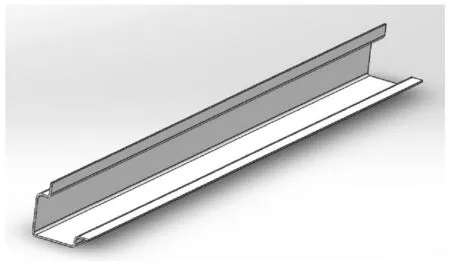
图2 集装箱角柱板材成品Fig.2 Finished Product of Container Corner Column

3 板材上下料机械手的结构简介

本文研究的基于2-P（Pa）并联结构的板材上下料机械手，如图1所示。

当机械手工作时，首先由折弯机A对板材进行图1（a）所示第一、二次折弯，然后由机械手抓取板材，转运至折弯机B处，进行图1（b）、（c）所示第三、四、五次折弯。机械手所需转运板材横截面即为图1（b）所示。在机械手对板材转运的同时，前端抓取机构实现对板材的翻转。

机械手的2-P（Pa）结构简图如图4所示，A、D表示机构中的两个移动载板，l1,l3表示2-P（Pa）并联机构两侧连杆，B、C表示连杆与抓取机构相连接的铰链，l3表示抓取机构位于两个铰链之间的长度，P点为抓取机构连同被抓取板材的质量中心，h表示P点与BC连线之间的垂直距离。当机械手工作时，由两条同步带分别带动A，D两个移动载板，通过控制两个移动载板之间的距离，改变连杆的转动角度，实现抓取机构沿y轴方向的上下运动。当移动载板A、D运动时，若两移动载板之间距离减小，则带动BC段下降；若移动载板之间距离增大，则带动BC段上升。通过两个载板沿导轨的横向移动实现抓取机构沿X轴方向的左右运动。

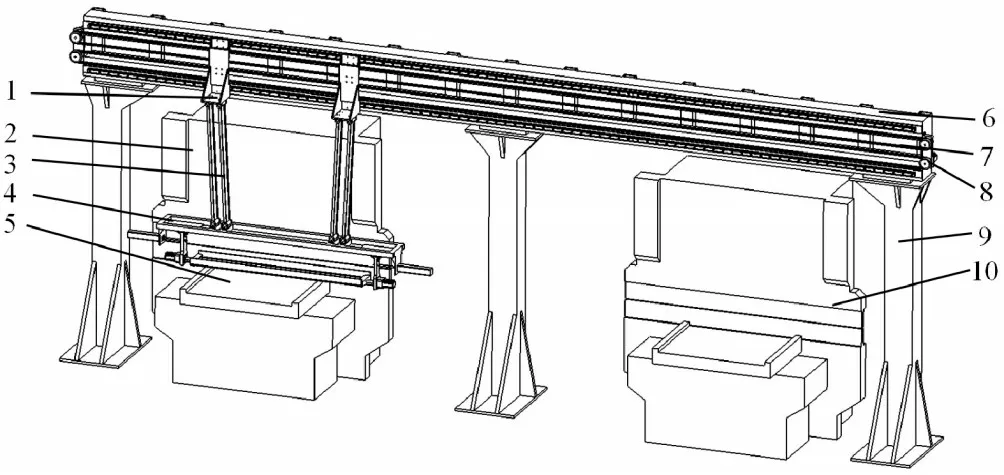
图3 集装箱板材折弯系统整体模型Fig.3 Overall Model of Container Sheet Bending System

图4 并联机构及抓取机构结构简图Fig.4 Schematic Diagram of Parallel Mechanism and Grabbing Mechanism

为了便于对并联机构进行运动学及动力学分析，首先建立了相对应的坐标系。在结构简图中，xoy为参考坐标系，其中o为参考坐标系原点，x轴沿AD方向，y轴垂直x轴向上；XPY为运动坐标系，P点为抓取机构质量中心，随着抓取机构一起进行移动，X轴平行于x轴，Y轴平行于y轴。

4 运动学分析

首先定义以下变量：（1）xi=[xA,xD]T，（i=A或D）为定义于参考坐标系的坐标矢量，其中xA,xD分别表示移动载板A，D沿x轴的位移。（2）Xp=[xp,yp]T为定义于运动坐标系的坐标矢量，其中xp,yp为运动坐标系XPY的坐标原点P相对于参考坐标系xoy的坐标。

由已知并联机构主动件参考坐标的位置，求解出抓取机构位于运动坐标系的位置，称为机构位置的正解。反之，如果已知抓取机构位于运动坐标系的位置，由此推出并联机构主动件参考坐标的位置，称为机构位置的逆解。

首先由结构简图4所示坐标系与结构尺寸的关系可以导出P点位置方程：

由图4几何关系得：

再将式（2）代入（1），可得P点运动方程的正解：

再由式（3）可得P点运动方程的反解：

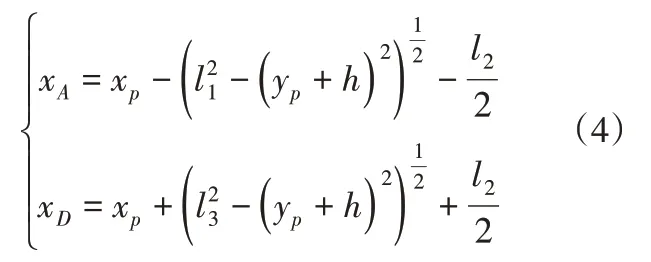
将上面求得的运动方程（4）对时间求导，便可得到速度方程：

再将速度方程（5）对时间求导便可求出加速度方程：

5 动力学学分析

在前面运动学分析的基础上，以2-P（Pa）并联机构为研究对象，利用拉格朗日法进行动力学分析。

在求解并联机构的的动力学方程时，拉格朗日函数为并联机构动能与势能的差值，即：

式中：L—拉格朗日函数，T—并联机构的动能，V—并联机构的势能。

在此机械手的并联机构中，需要分析的刚体包括：移动载板、连杆、抓取机构（包括被抓取板材）。在此假设两侧连杆长度相同，且为均质连杆。

5.1 计算机械手的拉格朗日函数

基于参考坐标与运动坐标计算连杆的动能：

首先将连杆质心坐标表示为关于参考坐标与运动坐标的关系函数，设杆l1，l3的质心坐标为(x1,y1)，(x3,y3)，r1,r3表示连杆质心到与连杆整体长度的比值，则求解连杆的动能公式为：

基于参考坐标xi=[xA,xD]T，计算出移动载板的动能Ts，基于运动坐标Xp=[xp,yp]T，计算出抓取机构机架及板材的动能Tp，若ml1=ml3=ml，r1=r3=r，则求得机械手并联机构的总动能为：

式中，ms—移动载板的质量，mp—抓取机构机架的质量，mB—板材的质量，Ts—移动载板的动能，Tp—抓取机构机架的动能，

5.2 机械手的势能

势能的大小与零势能面的选取有关，分析此机械手的势能时，首先把板材被抓取前质心所在平面设为零势能面。由于两个移动载板的轨迹为水平横移，故其势能不变，即为0。抓取机构连同被抓取板材由最低点抬升至最高点的距离为H，设其势能为Vp；设连杆的势能为Vl，则机械手的势能：

式中：L—杆l1,l3的长度，θ10,θ30—机械手抓取机构运动至最低点时两侧连杆与水平轴向所成的角度，mp—抓取机构机架的质量，mB—板材的质量。

故可得机械手并联机构及抓取机构的拉格朗日函数：

5.3 求解动力学方程

将式（9），（10），（11）带入拉格朗日方程，最后并联机械手的动力学方程可表达为：

由并联机械手的动力学方程式（12）可知，当已知机械手所受外力及机构运动时，可求出移动载板所受力的大小。

6 仿真结果

结合集装箱板材折弯的流程，对机械手的运行轨迹进行规划。已知待转运的集装箱角柱板材质量为54kg，机械手由取料到放料完成所用时间为T=6s，抓取机构及板材质心初始点为（0，0），末端点为（4，0），抬起高度为0.4米，为了机械手运行顺畅，运行轨迹连续、光滑，采用正弦加速度函数规划其运动轨迹如下：

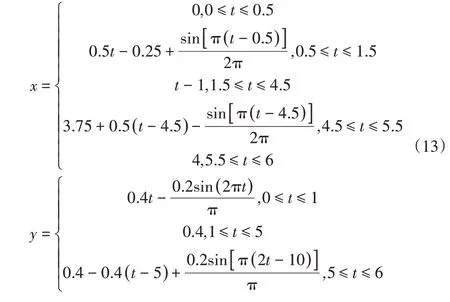
由此运行轨迹可知，机械手在起始位置及末端位置的速度及加速度为0，保证了机械手运行的平稳性，减小了机械振动，实现板材安全、高效的转移。

忽略摩擦力，给定重力加速度g=9.8m/s2，利用Matlab软件对机械手的动力学方程（12）进行计算，得出移动载板所受驱动力的变化曲线，如图5所示。

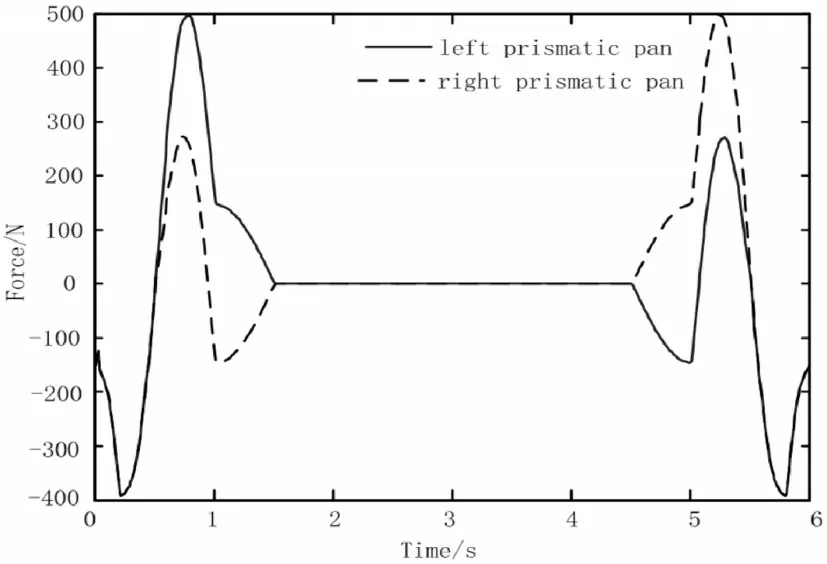
图5 理论驱动力曲线Fig.5 Theoretical Driving Force Curve

从图5中可以看出，机械手抓取板材后开始抬升时计时，0-1秒期间，两个移动载板同时分别向两侧移动，带动抓取机构抬升，这其中两个移动载板都经历了加速度由小变大再由大变小加减速过程，驱动力也随之变化；1-1.5秒两个移动载板同时向x轴正向加速移动，加速度逐渐减小，所受驱动力逐渐减小，1.5秒后加速度变为0，两个移动载板作匀速运动，驱动力趋于零；4.5-5秒两个移动载板作减速运动，加速度逐渐增大，驱动力也再变大，移动至下料位置斜上方后，移动载板A继续向x轴正向移动，移动载板B开始减速；5-6秒期间，移动载板B开始向x轴负向移动。此时，机械手抓取板材向下移动，其中两个移动载板都经历了加速度先由小变大后再有大变小的加减速的过程，其所受驱动力也随之变化，如图5所示。

为了更近一步验证动力学方程的正确性，首先在ADAMS软件中建立机械手的仿真模型，利用式（13）所得的轨迹曲线，对上下料机械手进行动力学仿真。然后，经过后处理得出机械手载板的驱动力曲线如图6所示。最后，对理论驱动力变化曲线与仿真驱动力变化曲线进行对比，得到的误差变化曲线如图7所示。从图7可以看出，理论值与仿真值在±5N范围内，误差值较小，验证了运动学和动力学模型的正确性。据此可为初选驱动元件，并进一步进行结构优化设计和控制研究。

图6 ADAMS仿真测得的载板驱动力曲线Fig.6 Carrier Driving Force Curve Measured by ADAMS Simulation

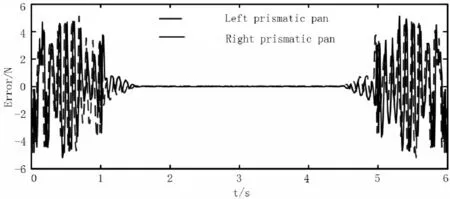
图7 驱动力误差曲线Fig.7 Driving Force Error Curve

6 结语

针对集装箱角柱板材上下料的需要，提出了一种采用2-P（Pa）并联机构与抓取机构相结合的机械手，实现折弯工序对板材的快速搬运；利用解析法推导出了并联机构的位置反解、末端执行机构的速度方程；基于拉格朗日法建立了机械手的动力学模型，规划一种实现机械手运行平稳的运动轨迹，并采用ADAMS软件进行了实例仿真验证。验证结果表明：理论值和仿真值的误差在±5N范围内，误差值较小，验证机械手运动学模型及动力学模型的正确性，为机械手后续的动载分配优化及系统控制等提供了理论指导。