双螺旋线圆柱凸轮机构的设计与分析

魏俊杰，朱家诚，杨 徐,谢佳奇

（合肥工业大学机械工程学院，安徽 合肥230009）

1 引言

凸轮机构被广泛运用于轻工、纺织、食品、交通运输、机械传动等领域。圆柱凸轮机构是在一个圆柱面上开有曲线凹槽或在圆柱端面上做出曲线轮廓的构件，它可以看做是将移动凸轮卷成圆柱体而演化来的。

应某企业要求设计一款安装在机械手末端实抓手的螺旋运动，圆柱滚子凸轮的传动平稳，能够实现长期高效的往复运动。考虑到如果仅存在单侧滚子长期运动会对圆柱凸轮的中心轴线产生倾覆力矩，不利于机构的高效稳定运行，故设计了空心圆柱两侧装配双滚子。轮廓曲线是空间圆柱凸轮设计的重点，空间圆柱凸轮轮廓曲线的设计方法一般采用图解法和解析法。采用解析法对凸轮轮廓进行设计，并在此基础上采用图解法选取特殊点对设计过程进行简化优化，利用Adams2016软件中的接触分析对凸轮运动进行模拟仿真，将得到的运动状况反馈进行结构的调整。反复进行上述操作对机构的运动拟合，实现的机构长期、平稳、高效运行。

2 企业提供机械手的工作原理

某企业提供的工业机械手，利用NX10.0进行简单建模［1］，结构模型如图1所示。工业机械手主要由抓手1、小臂2、大臂3、底座4及相关附件装置组成。工业机器手的抓手的啮合抓取运动是由气缸直接拉动抓手内部弯钩部分，抓手绕抓手座完成旋转，抓手座上安放了四个抓手，当气缸运作时带动完成啮合。

图1 某企业工业机械手模型渲染图Fig.1 Rendering Diagram of an Enterprise Industrial Robot Model

应某企业的要求机械抓手需要完成以下操作：机械臂末端抓手在向内闭合夹紧工件的同时需要完成轴向位移50mm与旋转90°以对完成对抓手夹紧工件的旋转以及拉拔。经分析，为使连接平滑、稳定且轻巧。故采用螺旋线圆柱滚子凸轮，考虑到只采用单个滚子的接触传动会使整体构件承受较大的倾覆力矩，故采用双滚子进行对称设置安放，螺旋线镜像分布，双滚子的采用平衡了构件受到单个作用的力矩，使得传动不会偏离螺旋线轨迹。此外，与传统圆柱滚子传动不同，经对抓手以及小臂进行结构分析，采用滚子中心不动，而圆柱凸轮机构自身旋转且沿轴向位移运动也是本方案的一个创新点。

3 双螺旋线滚子圆柱机构的设计

3.1 机构原理解析法分析

圆柱螺旋线是一种常见的螺旋线，当一个运动的点沿着圆柱面的母线做匀速直线运动，同时圆柱自身做绕着轴线的匀速转动时，点实际上进行的复合运动轨迹称为圆柱螺旋线，圆柱螺旋线有三个要素：螺旋线直径D、导程H及旋向。依据圆柱凸轮在空间中的分布建立坐标系如图2所示。选取圆柱凸轮底面中心为坐标中心，俯视图上建立x-y坐标系，Z轴垂直于xy平面。滚子在t时间内旋转过的角度在xy平面上的投影为γ，应企业要求需要在旋转90°的同时完成轴向完成

图2 圆柱凸轮俯视图Fig.2 Cylindrical Cam Top View

50mm的位移。经查阅资料与分析，选取圆柱底面半径R为30mm，故分析得螺旋线的螺距为200mm，因企业只需完成90°的旋转，所以螺旋线理论上只需要1/4圈。由上述可得螺旋线的方程为：

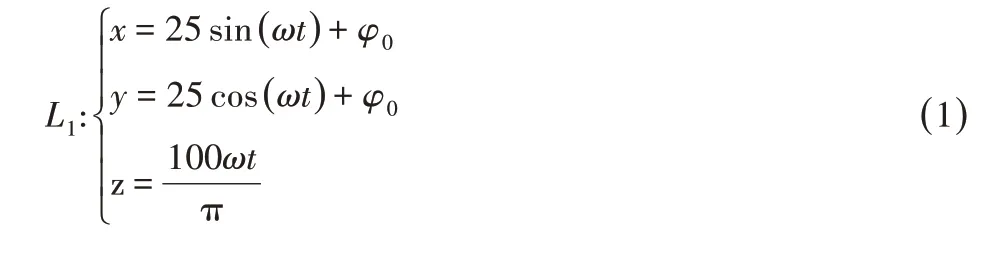
式中：φ0—初始角度，由于此处仅仅为得到双螺旋线的实际轨迹，只需要选择初始角度为0，并设置ω为1，这样赋值是为了当t取π/2时刚好完成螺旋线轨迹的建模。

圆柱凸轮［3］是受气缸拉动向后做螺旋运动，此时滚子质心不动。依据作用力相对原理圆柱滚子受到圆柱凸轮的反作用力如图所图4所示，由于双螺旋线依据z轴呈中心对称结构，故我们只需要研究单个滚子的受力以及运动状况，由于研究变力比较困难，故将气缸提供的无规律力等效成作用力肥F，F是滚子受到圆柱凸轮的反作用力沿着圆柱凸轮z轴方向，式中：Fn是F垂直于运动方向的分量，F与Fn之间的夹角为螺旋角β,Fτ是F沿着运动方向分量。υt是t时刻滚子中心O的瞬时速度，υz是υt在Z轴方向上的分量，υxy是υt沿着圆柱面切线的方向在xy平面上的投影，υt与υxy之间的夹角为螺旋角β。

由图可得（3）、（4）：

故结合图2与图4可以得到滚子在t时刻的各方向瞬时。

图3 圆柱滚子受力与运动示意图Fig.3 Schematic Diagram of the Force and Motion of Cylindrical Rollers

加速度：

公式中的加速度依据图1建立的坐标系确定方向，注意，由于是通过滚子研究凸轮，故公式中的m均为圆柱凸轮与抓手的质量之和。由于ax、ay中含有滚子的转角γ，故需要得到γ与时间t的关系式，如（8）、（9）、（10）：

式中：axy—t时刻加速度at在xy平面上的投影，ε—瞬时角加速度，ωt—瞬时角速度，θt—t时刻滚子转过的角度。将得到的γ带入ax、ay中得到ax、ay关于t的关系式：

将ax、ay、az关于t的函数解析式导入matlab2016在0-t上对t进行积分就能得到t时刻x、y、z方向上的瞬时速度如公式（13）、（14）、（15）：

式中：fresnelc(t)、fresnels(t)—菲涅尔函数的两种形式。至此，利用解析法完成了对t时刻滚子的受力以及运动状况分析。

3.2 模型结构的仿真分析

本节采用软件模拟对3.1结构的解析法进行验证。结构模型采用NX10.0建立，渲染后如图4所示，圆柱凸轮直径为50mm，螺旋线导程为200mm，这里我们需要的轨迹为1/4的周期，两圆柱滚子［4］安装在中间轴上，里侧轴肩限位，外侧利用轴套限位，轴套外侧利用螺母固定防松。双滚子通过轴连接，凸轮连接机械抓手部分。当抓手受到拉力向内夹紧啮合时，凸轮机构会带动抓手做通过双滚子做螺旋运动。

图4 双滚子螺旋线圆柱凸轮模型渲染图Fig.4 Double Roller Spiral Cylindrical Cam Model Rendering

结构模型在NX10.0中完成装配，将装配体导入adams2016，完成各部件的约束，由于运动的性对性，研究时候将圆柱凸轮机构作为固定部件，研究滚子的运动以及受力状况，结构是关于z轴对称分布的，故只需研究单侧即可。经分析，双滚子在切槽中的运动可以近似为纯滚动。研究重点是滚子质心的运动状况，所以在Adams2016［5］中可以采用轨迹仿真法，利用Adams2016中建立仿真曲线，定义滚子质心与螺旋线进行point-curve配合接触，滚子质心只能按照式（1）、（2）生成的拟合螺旋线路径进行运动。滚子与螺旋切槽之间的接触设置摩擦系数为0.15，碰撞动力损失为0.1。凸轮采用1body 1location与ground进行bonded固定限制其所有自由度。将公式（1）导入Matlab中得到实际滚子的运动轨迹，此时选用ω=π/2，在t∈（0，0.5）区间内进行0.025间距描点，将这21个坐标导入Adams建立marker点，用样条线顺次连接这些marker点，由于轨迹长度短，描绘的marker点多，故这种方法做出的样条线与螺旋线之间的拟合效果非常好。设置质量m为4.5kg，气缸拉力为220N，拉力F直接作用在质心m上并沿Z轴负方向，选择move with part力跟随物体进行运动以达到模拟真实拉力的情况。由于本运动为1/4周期，故需要在Adams2016中设置传感器，当质心运动到Z坐标接近0时停止运动，设置阀值为0.01。进入Adams simulation［6］中进行仿真运动，设置运算步数为1000。运算完成进入Adams后处理模块，绘制质心的x、y、z方向位移，x、y、z方向速度的曲线图，如图5所示。

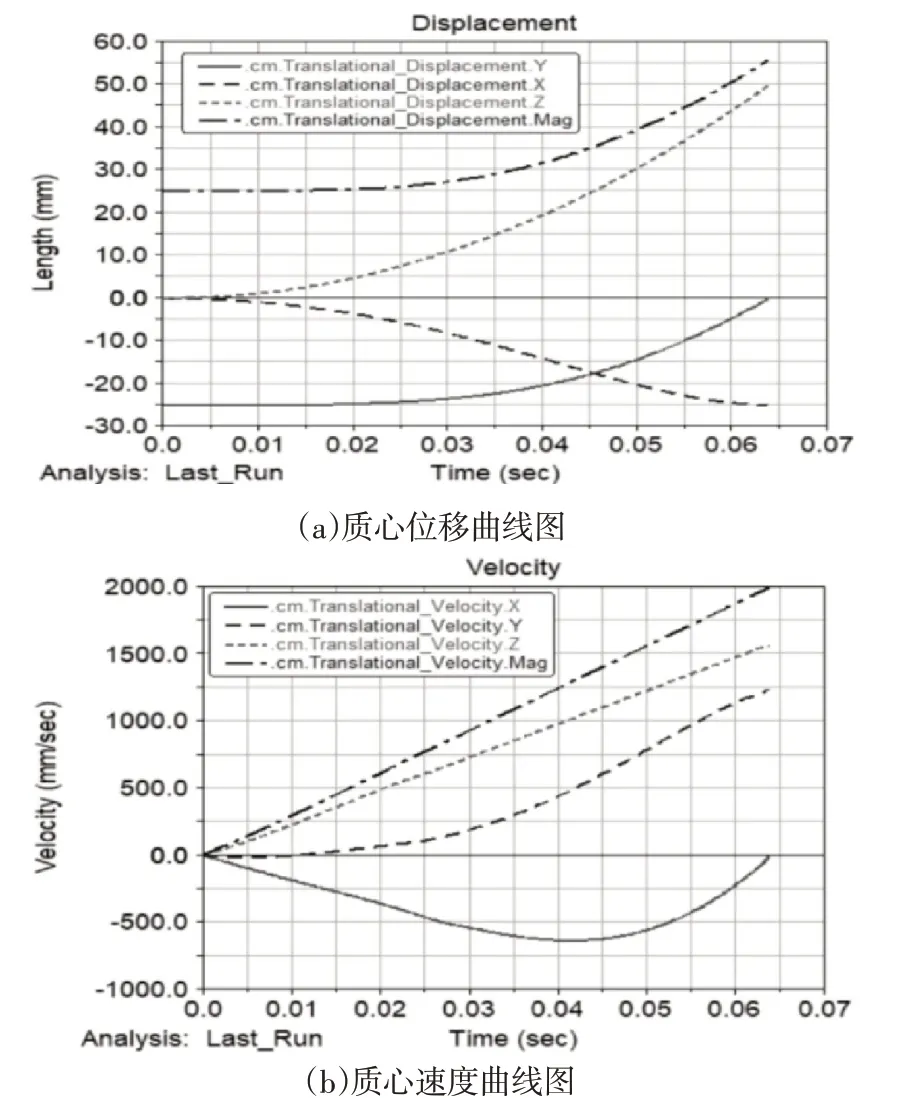
图5 运动曲线图Fig.5 Motion Curve

图5-a反馈的质心位移曲线与式（1）、（2）一致，说明螺旋结构的建立与实际相当吻合。观察图5（b），分析得各曲线与式（13）、（14）、（15）得到的结果符合，验证了解析法。分析图5（b）发现运动结束时速度高达2m/s，且流程执行时间仅仅只有0.065s，较短的时间内造成的冲击振动会对整个结构的平稳运行产生巨大挑战，故考虑在行程25mm处设置弹簧减少冲击，图6为分别选用k为0～18N/mm的弹簧进行减振后的模拟效果，图6表明增加弹簧刚度K能够减小撞击接触的速度同时增加行程时间，但提高弹簧压缩后太大的弹簧预紧力会对结构造成较大的回弹作用力，不利于前置抓手的抓紧状态的保持，当K取到18N/mm时行程时间也未能达到0.08s，故仅仅增加弹簧刚度K对行程时间未能起到明显的缩短。

图6 改变弹簧刚度K运动曲线对比图Fig.6 Change the Spring Stiffness K Motion Curve Comparison Chart

经分析采用阻尼减振对短时间内减速具有很高的效率，故设置设弹簧，仅仅采用阻尼减振进行对比仿真。如图7所示，仿真采用阻尼系数分别为0～0.8共9组数据进行对比，仿真结果表明采用阻尼进行减振对增加行程时间，能够显著降低冲击速度。如图7所示当选取阻尼为0.8时候能够直接将速度降低到250mm/s，且行程时间能够加大到接近0.25s对减小冲击意义重大。

图7 改变阻尼系数运动曲线对比图Fig.7 Change the Damping Coefficient Motion Curve Comparison Chart

经分析单采用刚度较大的弹簧容易产生较大的反作用弹力不利于凸轮机构稳定状态的保持，单采用高阻尼进行减振容易降低机构的灵活性，不利于机构的高效运作。因此在有限的条件下，本课题是研究在选用合适大小的弹簧刚度K值的条件下，配合选用合适大小的阻尼进行联合减振，选用5N/mm的K值时，阻尼系数分别为0.2～0.6共九组仿真数据，如图9所示。

图8表明，选用5N/mm的弹簧刚度配合0.3以上的阻尼减振能够非常有效的将速度从开始的2m/s降低到0.2m/s以下，并且能够将行程时间增加到接近0.3s，这是非常符合预期的效果。表1是阻尼系数选择在0.25～0.45区间内5组行程时间与接触冲击速度。

图8 弹簧与阻尼联合减振运动曲线对比图Fig.8 Spring and Damping Combined Damping Motion Curve Comparison Chart

表1 采用弹簧与阻尼减振后的时间与速度Tab.1 Spring and Damping Combined Damping Time and Speed

由表1进行对比发现冲击速度在阻尼系数0.25～0.35之间下降的特别快，在阻尼系数达到0.4s后降低的并不是特别显著。且总行程时间能够达到0.15s之后很好的契合了实际需要。故在弹簧刚度K值选取为5N/mm时，阻尼参数选取为0.35是非常适宜的。采用弹簧与阻尼并用减振机构在很大程度上增加了机构运动的可持续平稳高效的运行，这在改进设计后的现场实际运行过程中得到了证实。

4 结论

本课题以双螺旋线滚子圆柱凸轮为研究对象，从螺旋线的轨迹方程出发，采用解析法对机构的受力以及运动进行理论分析。利用NX10.0建模，将模型导入Adams2016输出其运动数据，对解析法结果进行验证。对设计初期得到的滚子与螺旋切槽的接触冲击进行分析，利用Adams对机构分别只采用弹簧及阻尼减振进行拟合分析，分析对比最后采用在合适的弹簧刚度条件下对适中的阻尼系数下进行拟合仿真。最后确定了本双滚子圆柱凸轮机构的减振模型采用弹簧及阻尼联合减振，并确定了弹簧与阻尼的具体优化参数。使用上述手段能够有效的解决机构运作不稳定因素，更好的实现了机构连续、平稳、高效的运作。