多维数据关联的机器人运动步态识别方法

陈先睿

（贵州大学体育学院，贵州 贵阳550025）

1 引言

现阶段指纹、人脸等生物特征识别技术在足球训练、交通以及工业等领域中已经有了十分广泛的应用［1-2］。但是这些生物特征的获取需要依靠近距离或者接触性的协作感知方法，而且这些信息容易伪装或隐藏，所以生物特征识别技术的应用范围受到了一定的限制，因此一种全新生物特征引起了相关专家的广泛关注，这就是步态。例如文献［3］提出一种基于确定性学习的人体步态识别方法，利用人体运动捕捉设备获取关节角时序数据序列，其中局部准确的人体步态内部动力学能够采用径向基函数网络得到逼近，根据将NN逼近获取的步态动力学知识存储在RBF网络中，利用该网络有效进行步态识别；文献［4］提出一种基于MPSO-BP神经网络方法的人体步态识别方法，主要采用自适应调整学习因子组建MPSO-BP神经网络分类器，通过多种传感信息的特征向量样本集对神经网络进行训练，以实现不同运动模式的步态识别。以上方法虽然在现阶段取得了较好的研究成果，但是这两种方法的识别有效率并不是十分理想。为了有效克服上述方法存在的问题，提出了一种基于多维数据关联的机器人运动步态识别方法。

2 机器人运动步态识别方法设计

以下给出基于多维数据关联的机器人运动步态识别流程图，如图1所示。

分析图1可知，基于多维数据关联的机器人运动步态识别流程为：采用背景减除法提取机器人运动图像，通过形态学方法去除所提取到的图像中的噪声及空洞。采用多维数据关联提取机器人运动步态轮廓形状静态特征，在此基础上获取动作能量图（AEI）以及步态能量图（GEI），并对二者进行对比分析，获取动态能量信息。采用核主成分分析进行空间降维，获取运动目标的频率动态特征，将机器人运动步态轮廓形状静态特征与频率动态特征进行融合，根据融合结果实现机器人运动步态识别。

图1 基于多维数据关联的机器人运动步态识别流程Fig.1 Robot Gait Recognition Process Based on Multidimensional Data Association

2.1 预处理

为了更加全面对机器人运动步态识别方法进行深入研究，由于机器人运动步态识别率的高低和运动目标轮廓提取的准确与否存在直接关联性［5］，因此首先需要在轮廓背景中对机器人进行分离。

背景减除法最为关键的一个步骤就是背景建模，其中时间平均图像为典型的背景模型，主要是将连续输入的N幅图像像素值的中间值设定为背景图像的像素值，同时设定{Ik,k=1,…,N}代表一个含有帧图像的序列，其中背景图像能够表示为：

式中：Ik(x,y)—第k帧图像(x,y)处的灰度值；B(x,y)—背景图像中(x,y)处的灰度值。

步态序列图像主要是通过背景减除法得到机器人运行目标，但是其中含有大量的空洞以及噪声，将会降低整个识别方法的有效识别率，所以通过形态学方法消除图像中存在的噪声以及空洞。

2.2 机器人运动步态特征选择与提取

机器人运动步态特征提取是机器人步态识别技术中十分关键的一步，特征提取是实现步态识别的基础［6-7］，因此以下通过多维数据关联进行采样，在采样前期需要将(x,y)坐标转换为(θ,r)，同时将各帧图像轮廓的质心设定为(xc,yc)，将其作为变换后的极坐标原点，具体的转换公式如下所示：

长度计算式为：

通过公式（4）以及公式（5）计算轮廓的质心：

在完成采样之后，还需要将极坐标转换为直角坐标，方便后续进行Procrustes形状特征提取［8］。假设极坐标为(θ,r)，则通过公式（6）将其转换为直角坐标，即：

设定步态序列为F={f0,f1,…,fN-1}，ft代表第t帧图像序列，N代表一个周期步态序列的帧数，首先需要计算两个相邻图像的帧差图，即：

AEI能够定义为：

ARI中包含步态图像中大量的动态信息，能够通过不同像素点的强度代表在行走过程中具有动态变化性的像素点中出现的概率。

机器人在行走过程中，主要通过姿态变化、手臂摆动幅度以及用力大小进行情况进行运动步态的识别，但是这些特征需要在一个完整的步态序列图像中获取，因此以下重点采用步态能量图展开研究：

设定一组步态周期图形序列为At()x,y，采用以下公式计算步态能量图：

将AEI和GEI两者进行对比分析，获取大量的GEI动态能量信息，实现机器人运动步态特征提取。

2.3 机器人运动步态识别

核方法属于一类模式识别方法［9］，整个方法最为主要的目的就是得到一组数据之间的关系，主要通过核函数完成数据处理，同时降低算法的计算量。

设定x,y∈X，其中X代表数据空间的样本集，分式线性性映射函数为Φ，则有：

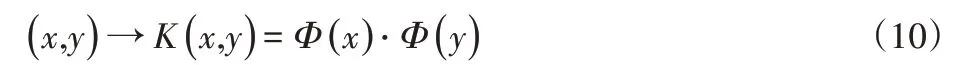
式中：K(x,y)—核函数；Φ(x)·Φ(y)—内积。

只有满足对应条件的核函数才能够应用在核方法中，具体的判定过程如下。

针对于任意给定的函数K(x,y)，不恒等于零的函数g(x)促使∫g(x)2dx＜∞是函数K(x,y)能够在特征空间进行内积运算的充分必要条件，其中：

采用核主成分分析方法进行步态特征降维的过程中，首先需要针对F空间的总体样本协方差矩阵SΦ t的特征值进行分解，则有：

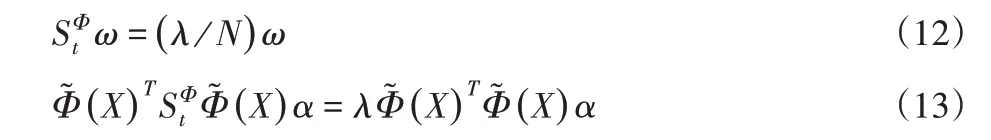
核主成分分析算法的具体计算过程如下所示：

（1）将函数K设定为训练特征集S的核函数；

（2）计算核函数全部对应的核矩阵，同时计算矩阵K~；

（3）对矩阵K~进行特征值分解，将得到的特征值按照从大到小的顺序进行排序，选取前i个特征向量；

（4）最后得到降维之后的数据，其计算公式如下：

通过降维处理之后能够得到运动目标的频率动态特征。

通过公式（15）计算各个特征的权重值：

将公式（15）中的算法应用到加法融合公式之中，获取加权的加法融合规则，具体的计算公式如下：

式中：gi—总特征；Rn—第n个特征子向量。

通过两个特征的融合，能够实现机器人运动步态识别［10］。

3 仿真实验

实验主要以人形仿生机器人为对象进行研究，数据库共含有人形仿生机器人20台，针对不同的人形仿生机器人进行15个不同角度的拍摄，每个机器人在同一个视角下共包含10个步态序列。

选择文献［3］方法、文献［4］方法作为实验对比方法，实验主要通过个人电子计算机（Inter Pentium（R）CPU3.00GHz，1GB RAM）完成。其中，实验用人形仿生机器人，如图2所示。

图2 实验用人形仿生机器人Fig.2 Humanoid Robot for Experiment

（1）为了针对不同识别算法的性能进行对比，实验选取机器人运动步态特征提取准确率作为方法评价指标，针对选取的20台人形仿生机器人的不同视角序列进行实验。在具体实验的过程中，选取4组图像作为训练集，剩余的部分则作为测试集，具体的实验对比结果，如表1所示。

表1 特征提取准确率变化情况Tab.1 Change of Feature Extraction Accuracy

由表1中的实验数据可知，研究方法的机器人运动步态特征提取准确率在96.22%-99.36%之间，说明这种方法的提取准确率较高，这说明该方法能够准确提取到机器人运动步态特征，能够为后续机器人运动步态识别奠定坚实的基础。

（2）为了进一步验证研究方法的鲁棒性，采用三种方法进行有效识别率对比，结果如图3所示。

图3 有效识别率对比结果Fig.3 Comparison Results of Effective Recognition Rate

从图中能够看出，进行特征融合之后，研究方法的有效识别率有十分明显的上升趋势，并且这种方法的有效识别率在82%-98%之间，始终高于实验对比方法。

（3）为进一步比较不同方法进行机器人运动步态识别的性能，进行识别耗时比较，结果如图4所示。

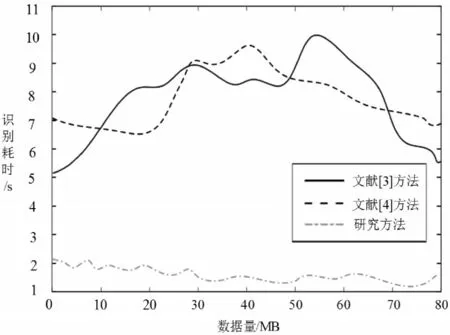
图4 识别耗时比较Fig.4 Comparison of Recognition Time

分析上图可知，研究方法的识别耗时在2.2s以下，始终低于实验对比方法，说明该方法能够快速识别机器人运动步态。

4 结束语

针对传统的机器人运动步态识别方法存在有效识别率较低等问题，结合多维数据关联，提出了一种基于多维数据关联的机器人运动步态识别方法。从实验结果分析可知，研究方法的机器人运动步态特征提取准确率在96.22%-99.36%之间，有效识别率在82%-98%之间，识别耗时在2.2s以下，说明这种方法的机器人运动步态特征提取准确率更高，且能够实现机器人运动步态的快速准确识别，获取较为满意的识别结果。