一类广义Dedekind和的上界估计

徐哲峰,王健康

(西北大学 数论及其应用研究中心, 陕西 西安 710127)

1 主要结果

设q>0为整数,h是与q互素的任意整数,经典的Dedekind和s(h,q)定义如下:

其中((x))表示一种锯齿形函数

这里(h,q)=1且h>0。

一些学者研究了与Dedekind和相类似的和式。2000年,Todd Cochrane介绍了如下Cochrane和:

其中d(q)是除数函数。Dedekind和与Cochrane和还有许多有趣的性质, 它们与著名的Kloosterman和也有联系[6-17]。

文献[9]定义了如下的高维Cochrane和

并给出了如下上界估计。

命题1设整数q≥2且整数h满足(h,q)=1。对任意固定的正整数k满足(q,k(k+1))=1,有

这里ω(q)表示q的不同素因子的个数。

文献[6]利用高维Kloosterman和的上界改进了命题1中的结果，并得到如下结果。

命题2设整数q≥2且整数h满足(h,q)=1。对任意固定的正整数k,有估计

本文定义了一类新型的广义Dedekind和。对给定的正整数m,定义

有趣的是，Cφ(q)-1(h,q)=C(h,q)和C1(h,p)=s(h,p),这里φ(q)表示Euler函数。这说明Cm(h,q)是Dedekind和与Cochrane和的广义形式。定义

很明显S1(h,q)=s(h,q),Sp-1(h,p)=C(h,p)，并有上述两者广义Dedekind和Cm(h,q)与Sm(h,q)之间的关系如下：

本文利用特征和的一些性质将Cm(h,q)与包含Gauss和的Dirichlet级数建立了联系, 并利用二项指数和估计,得到了广义Dedekind和Cm(h,q)的上界, 结论如下。

定理1设整数q≥2且整数h满足(h,q)=1。对任意固定的正整数m≠1,有上界估计

特别地,如果m是偶数, 则Cm(h,q)=0。

由定理1与两者新型广义Dedekind和之间的关系可直接得到如下推论。

推论1设整数q≥2是无平方因子数且整数h满足(h,q)=1。对任意固定的正整数m≠1, 有上界估计

特别地,如果m是偶数,则Sm(h,q)=0。

2 一些引理及定理的证明

本节将给出一些引理并完成定理的证明。

引理1令m≥2是任意固定的正整数且整数n1、n2满足(n1,n2,q)=1,有上界估计

引理2设整数q≥2且整数h满足(h,q)=1。对任意固定的奇数m,有

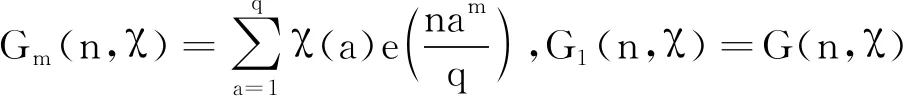
证明由Dirichlet特征的正交性, 可得

如果m是奇的，由于

Gm(-n,χ)=χ(-1)Gm(n,χ),

因此有

由此可得

“通过类比思想，分别过B、E、C三点向坐标轴引垂线段，可以转化为坐标轴上的中点坐标，进而得到坐标系内的线段中点坐标公式。如图3。

特别地,如果m是偶数,则

即证明了引理2。

引理3设整数q≥2且整数h满足(h,q)=1,Gm(n,χ)是引理2中定义的函数。对任意固定的奇数m≠1,有

证明对固定的参数N≥q和正整数m,根据Abel恒等式,有

显然有平凡估计

(1)

且由三角和估计可得

这里(ham)q表示ham模q的最小正剩余。因此有

(2)

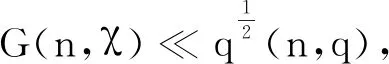
(3)

和

(4)

结合(1)—(4)式，可得

(5)

已知

对于m≠1，根据特征和的正交性，有

由此，再根据引理1，取(n1,hn2,q)=d1,(n1,-hn2,q)=d2,有

Ω1+Ω2。

(6)

先估计Ω1，已知

(n1,hn2,q)=(n1,(hn2,q))=(n1,(n2,q))，

因此，有

(7)

类似地，有

(8)

令N=q3,由(5)—(8)式可得引理3。

现在，结合引理2和3，有

即完成了定理1的证明。