带侵蚀燃烧效应的阶梯多根装药火箭发动机三维内流场特性
周柏航, 陶如意, 王浩, 阮文俊
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
0 引言
近年来,阶梯多根装药火箭发动机在大长径比、短距离、高效能的推力火箭中使用越来越多。药柱燃面与通气面积的比值简称燃通比,表达式为k=Ab/Ap,其中:Ab为该截面上游的燃面,表示流经该截面的质量流率;Ap为该截面上燃气通道的横截面积。因此,燃通比也表征该截面的气流速度,称为波别多诺斯采夫准则[1]。根据侵蚀燃烧定义,固体推进剂的燃速受平行于燃烧表面横向气流影响的现象称为侵蚀燃烧[1],从而燃通比成为影响侵蚀燃烧的一个重要因素。在固体火箭发动机设计中,为了提高质量比,要求壳体能承受较大的内压、装填较多的推进剂和具有较小的结构质量,通常采用阶梯多根装药[2]结构来大幅度提高火箭发动机的质量比[3]。这种设计结构使燃通比增大,侵蚀效应更明显,导致药柱燃速增加,燃烧室压强升高。因此从稳定性、安全性以及可控性的角度,必须对发动机工作过程的内流场进行精确预示,并深入分析影响固体火箭发动机工作过程的各个因素。
国内外对固体火箭发动机内流场进行了大量研究。关于点火瞬态内流场[4-6],杨乐等[7]采用自定义函数(UDF)对Fluent软件进行二次开发,用侧壁加质方式设定推进剂燃面,重点分析了发动机点火过程中压强上升的规律。关于常规装药工作过程[8-9],宋大明等[10]采用二维动网格UDF控制边界网格节点的方法仿真出发动机燃面的推移过程,得到燃烧室喷管一体化计算结果。关于考虑侵蚀燃烧模型二维内流场[11-12],唐必顺等[13]采用控制燃面节点移动为基础的动网格,对固体火箭发动机侵蚀燃烧的非稳态过程进行仿真,计算结果揭示了非稳态过程变化规律。关于火箭发动机试验[14-15],郑伟等[16]采用一种螺压改性双基推进剂装药的试验发动机,研究了初始通气参量、挡药架厚度、装药局部涂覆等对装药结构完整性的影响。
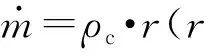
1 计算模型
1.1 物理模型
本文研究的固体火箭发动机考虑到燃烧室承受内压的燃通比等因素,最终确定燃烧室前级装19根药、后级装12根药。如图1所示,前后两级装药纵切面,按照此装药结构,前级装药内孔末端燃通比为144,前级装药外部末端燃通比为168.42,后级装药末端平均燃通比为141.49.图2所示为带坐标系的计算区域物理模型。
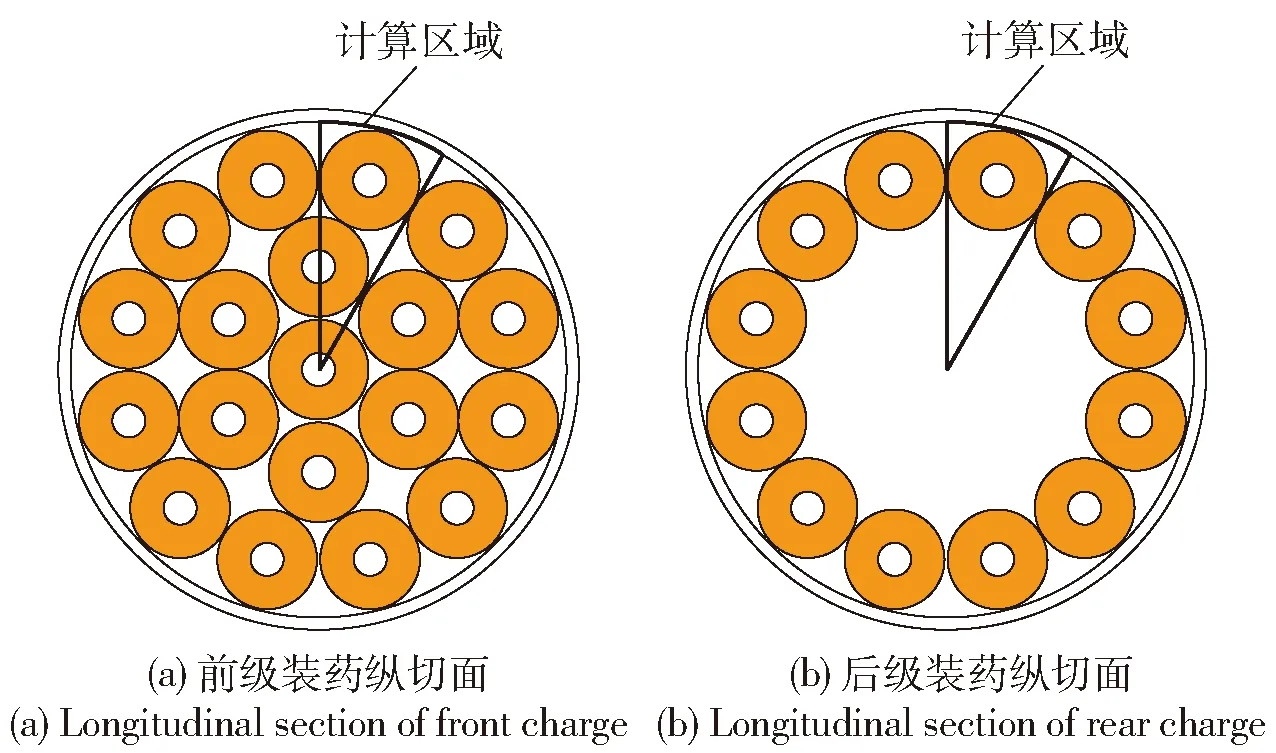
图1 前后两级装药纵切面Fig.1 Longitudinal sections of front and rear charges

图2 计算区域的物理模型Fig.2 Calculation domain of physical model
1.2 动网格方法和网格划分
为了处理计算过程中推进剂药柱燃面运动所引起的网格变化,需要采用动网格技术。动网格方法有铺层法、弹性光顺法和局部重构法。由于本文中药柱燃面运动是单向和镜像的运动,可以采用铺层法来实现对推进剂燃烧时药柱燃面运动的模拟。铺层法中需要对网格分割因子和合并因子进行设定,假设网格之间的尺寸为h,给定的理想网格尺寸为hi,网格分裂系数为cs,网格合并系数为ci,当新生成的网格尺寸满足h≥(1+cs)hi时网格被分割成两个,当网格尺寸满足h≤cihi时网格将合并为一个网格。本文算例中在压力上升段时期取hi=0.2 mm,cs=0.4,ci=0.05,在此之后直到药燃烧结束取hi=0.5 mm,cs=0.4,ci=0.05.
如图3所示,运用结构网格划分方法进行网格划分,考虑到装药结构的复杂性和对称性,最大限度进行简化取1/12进行多级分块三维结构网格建模。计算开始时网格数量约826万,由于动网格的存在,随着计算进行网格数量越来越多,到了计算结束900 ms时网格数量约为1 986.3万。图4所示为燃烧室前后段网格结构,在网格结构图上标注了每个质量入口燃面的位置。推进剂燃面在计算过程中内燃面扩大外燃面缩小,本文进行分块划分网格来实现铺层法动网格方法,在Fluent软件中设置各个网格块的重合面为interface,在interface中把相互连接的各个平面对应上,其中包括一对多和多对多,用对应面的方法来实现计算过程中各个网格块的重合面是相连通的。根据图2的坐标系和图4药柱的具体位置,设(x,y,z)为坐标系的节点坐标,(0,0)为药柱1中心点坐标,(0,y2)为药柱2中心点坐标,(x3,y3)为药柱3和药柱4中心点坐标。

图3 模型整体计算网格Fig.3 Computing grid of whole model

图4 燃烧室前段和后段网格结构Fig.4 Front and rear of combustion chamber grid structure
1.3 数学模型
根据几何燃烧定律,任何形状装药的Ab和Ap及其随时间的变化规律均可计算出来,由燃通比的定义k=Ab/Ap可得燃通比随时间的变化规律。用燃通比准则控制侵蚀燃烧效应,可以方便地与发动机装药设计直接联系起来,这是该准则的突出优点[2]。本文正是用燃通比这一可知参量与发动机侵蚀燃速系数联系起来。
为满足固体火箭发动机内流场数值模拟的需要,做出如下假设[3]:
1)只考虑固体火箭发动机内部结构的封头、燃烧室、推进剂、喷管;
2)点火过程与整个工作过程相比时间非常短暂,不考虑点火过程,假定点火药瞬间燃完火药气体均匀地充满整个内流场的压强、温度作为数值模拟的初始条件;
3)燃气服从完全气体状态方程;
4)对于大长径比固体双基推进剂忽略药柱的轴向燃烧只考虑纵向燃烧;
5)对于两级装药结构,前一级装药总燃面不变,燃气流出全部从后一级装药外侧流出,用侵蚀系数与燃通比的关系式确定每个网格节点的燃速。
对于侵蚀比模型,根据文献[17],得出双铅-2推进剂侵蚀燃烧侵蚀比燃速公式为
r=ε·apn,
(1)
式中:
(2)
根据各个燃面位置和药柱尺寸,得出每个燃面对应的导入UDF燃通比分别为
(3)
(4)
(5)
(6)
(7)
(8)
(9)
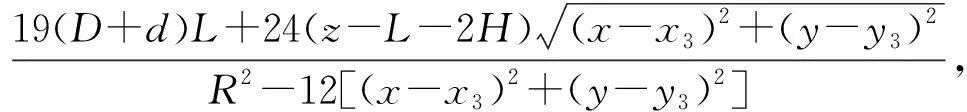
(10)
式中:ki为药柱内孔的燃通比;ke为药柱外部的燃通比;下标1、2、3、4分别为药柱1、药柱2、药柱3、药柱4;H为前中点火药位置空隙长度;R为燃烧室内部半径;L为药柱长度;d为药柱内径;D为药柱外径。(3)式~(10)式可以得出每个燃面的燃通比,导入(2)式中可以得出每个燃面具体节点位置的侵蚀系数ε,从而根据(1)式可以得出当前节点位置的燃速。由质量流率公式
(11)
得出当前节点位置的质量进口流率。
(12)
根据文献[17]得到平均侵蚀系数为
(13)
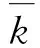
对于每个燃面的平均侵蚀系数对应的燃通比是取每个燃面末端上游的总燃面除以燃面末端对应的通气面积,根据侵蚀比模型中火箭发动机的参数计算出每个燃面对应的导入UDF平均燃通比为
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)

(22)
得出每个燃面的质量进口流率。
在Fluent软件中进行流场模型计算,选择三维基于压力瞬态求解器,流动问题为可压缩流动,湍流模型选择Realizablek-ε的湍流模型。设置求解器控制参数,耦合求解器选择Coupled,压力为Second Order离散格式,其余各个变量为2阶迎风离散格式。
1.4 初始条件及边界条件
1.4.1 初始条件
根据内弹道计算公式[18]
pB=fBωB/VB,
(23)
式中:pB为点火药全部燃完后的燃烧室压强;fB为点火药的火药力;ωB为点火药质量;VB为发动机总容积除去推进剂所占体积的密闭容积。试验所用点火药为黑火药,计算得火箭发动机内流场的初始压强为pB=4.237 MPa,设定初始温度为TB=2 500 K,各个方向初始速度为0 m/s.
1.4.2 边界条件
1)推进剂燃面设置为质量流量入口,以单位面积质量流率作为质量流出方式,根据(11)式和(22)式得出单位面积的质量流率,分别用UDF设置侵蚀比和平均侵蚀比两种计算模型。根据文献[19]设定固体推进剂燃烧温度为2 320 K,假设燃气的密度是空气的10倍,设置静压为8.6 MPa对应的侧壁加质燃气密度为12.93 kg/m3.
2)推进剂燃面设置成动网格边界,根据(1)式和(12)式得出燃速,分别用UDF设置两种计算模型,实现各个内燃面扩大和外燃面缩小。
3)喷管尾部与外界大气连接部位设置为压力出口条件,压力为101 325 Pa,温度为300 K.
4)网格上所有两侧的面设置为对称面,除去之前设置的质量入口、压力出口、连接面、两侧的对称面,把剩余的所有面设置为绝热壁面。
2 计算结果与分析
2.1 侵蚀比与平均侵蚀比模型对比分析
图5所示分别为燃烧室前部、中部、后部侵蚀比计算结果与平均侵蚀比计算结果压强对比图。

图5 侵蚀比模型与平均侵蚀比模型在燃烧室前部、中部、后部的计算压强对比Fig.5 Comparison of calculated pressures in front, middle and rear parts of combustion chamber by erosion ratio and average erosion ratio models
根据读取计算数据可知:燃烧室前部压强在20 ms时相差最大,侵蚀比模型计算压强比平均侵蚀比模型高0.39 MPa,两种模型计算结果相差2%左右;随着火箭发动机工作接近到平衡压强,差值越来越小,在150 ms时侵蚀比模型计算压强比平均侵蚀比模型高0.1 MPa,在200 ms之后直到推进剂燃烧结束,两种模型的计算结果基本一致。以同样方式读取两种模型燃烧室中部、后部压强数据,结果表明:燃烧室中部压强在20 ms时侵蚀比模型比平均侵蚀比模型高0.46 MPa,两种模型计算结果相差2.9%左右,在150 ms时侵蚀比模型比平均侵蚀比模型高0.2 MPa,在200 ms之后两种模型的计算结果基本一致;燃烧室后部压强在20 ms时侵蚀比模型比平均侵蚀比模型高0.41 MPa,两种模型计算结果相差2.7%左右,在150 ms时侵蚀比模型比平均侵蚀比模型高0.26 MPa,在200 ms之后两种模型的计算结果基本一致。根据以上计算结果分析可知:两种模型的计算结果在压强最高点处相差最大,相差小于3%在允许范围之内;随着火箭发动机工作相差越来越小,到达平衡工作压强之后两种模型计算结果基本吻合。表明两种模型用于大长径比阶梯装药结构的计算结果一致性比较好。
2.2 侵蚀比模型内流场分析
根据读取图5所示的计算结果可知:对于侵蚀比模型,燃烧室前部、中部、后部3个监测点在20 ms时基本都处在最大压强值,370 ms时处于平衡压强状态前期,550 ms时处于平衡压强状态中后期,770 ms时前级装药燃烧结束,775 ms时后级装药燃烧结束。图6所示为内流场的正切面E与斜切面G剖切位置示意图。图7所示为内流场的正切面不同时刻的压强分布图。图8所示为内流场的斜切面不同时刻的压强分布图。

图6 正切面E与斜切面G剖切位置示意图Fig.6 Schematic diagram of tangent plane E and diagonal plane G sections
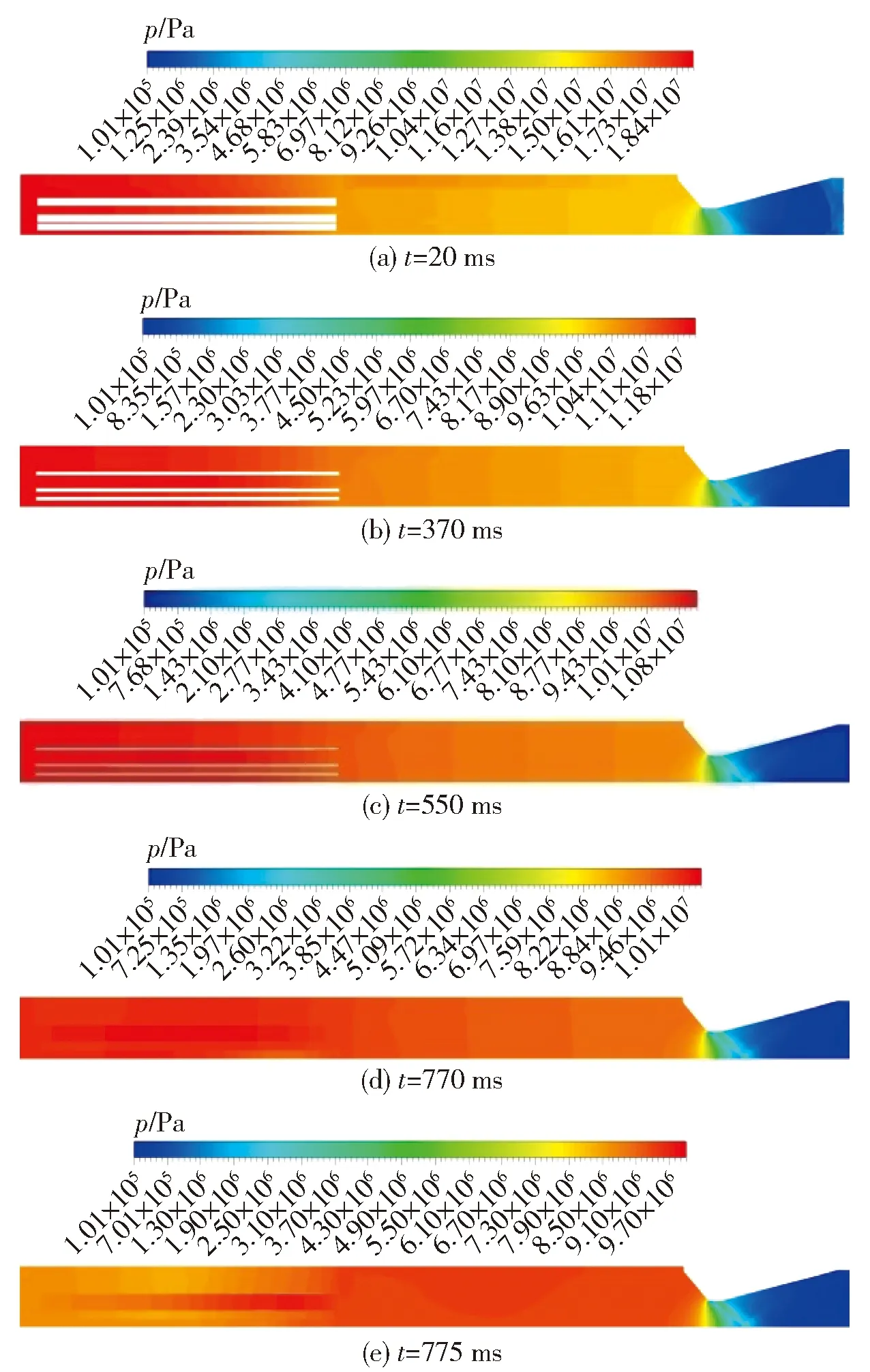
图7 不同时刻正切面的压强分布Fig.7 Distribution of pressure on tangent plane at different times
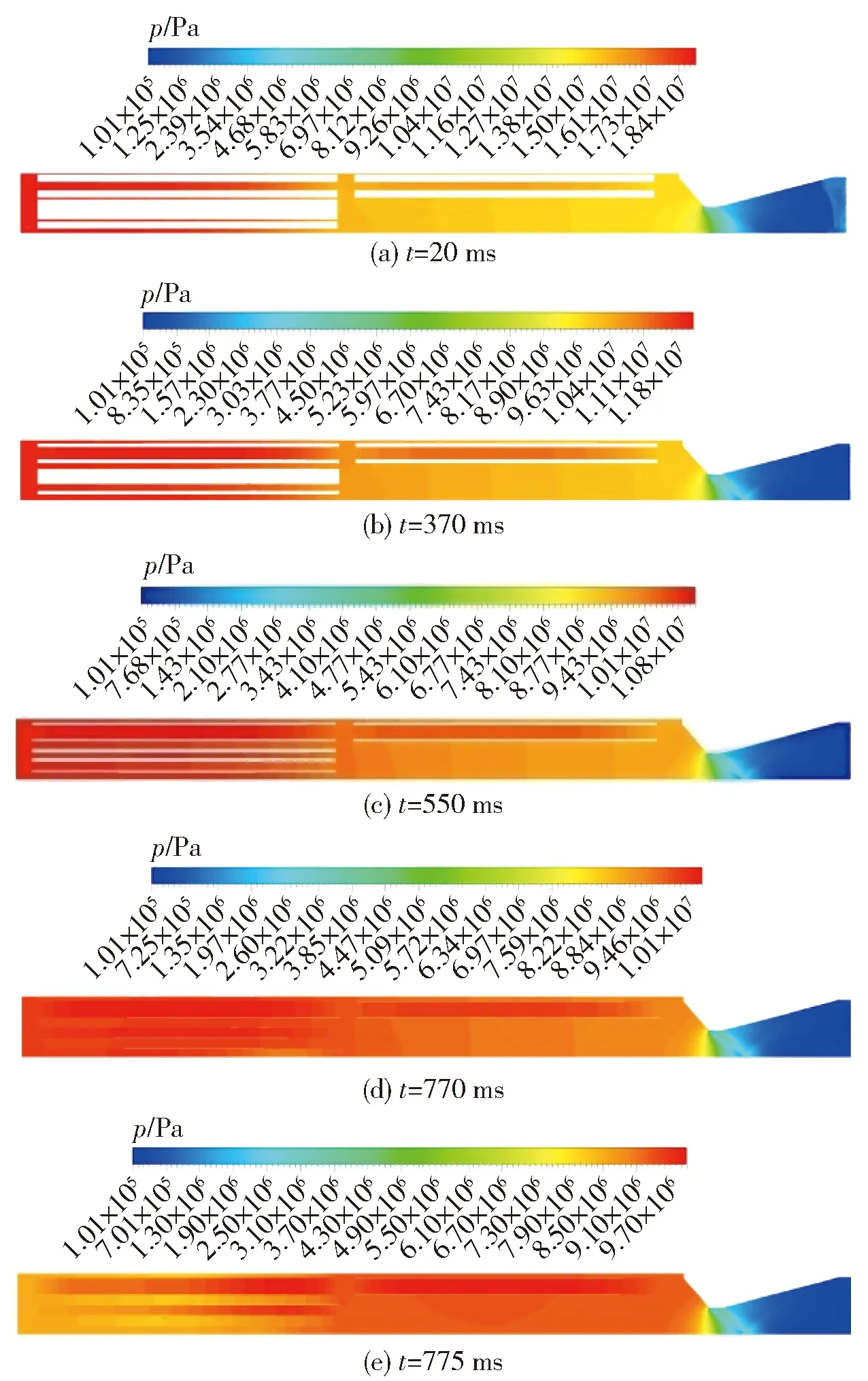
图8 不同时刻斜切面的压强分布Fig.8 Distribution of pressure on diagonal plane at different times
由图7(a)和图8(a)推进剂开始燃烧到压强上升到最高点(20 ms)的压强分布图可知,内流场的最高压强不超过20 MPa,从前部到后部逐渐减少,前部到中部减少3 MPa左右,中部到后部减少1 MPa左右。由图7(b)、图7(c)和图8(b)、图8(c)平衡压强时刻(370 ms和550 ms)分布图可见,药柱没有出现明显的侵蚀燃烧喇叭型,这是因为燃烧室前部压强高、后部越来越低,燃通比前部小、后部越来越大,通过侵蚀比燃速公式(1)式结合节点动网格计算结果,表明装药结构设计合理,避免了侵蚀燃烧对发动机工作过程的影响。由图7(d)、图7(e)和图8(d)、图8(e)两级装药燃烧结束时刻(770 ms和775 ms)分布图可知,前级装药燃烧先结束,两级装药燃烧结束时间不超过5 ms,前后压强差约1 MPa.
图9所示为各个药柱内外燃面压强差压强- 时间曲线,图10所示为各个药柱压强差约为最大值时(150 ms)前、后药柱中部纵切面的压强分布。
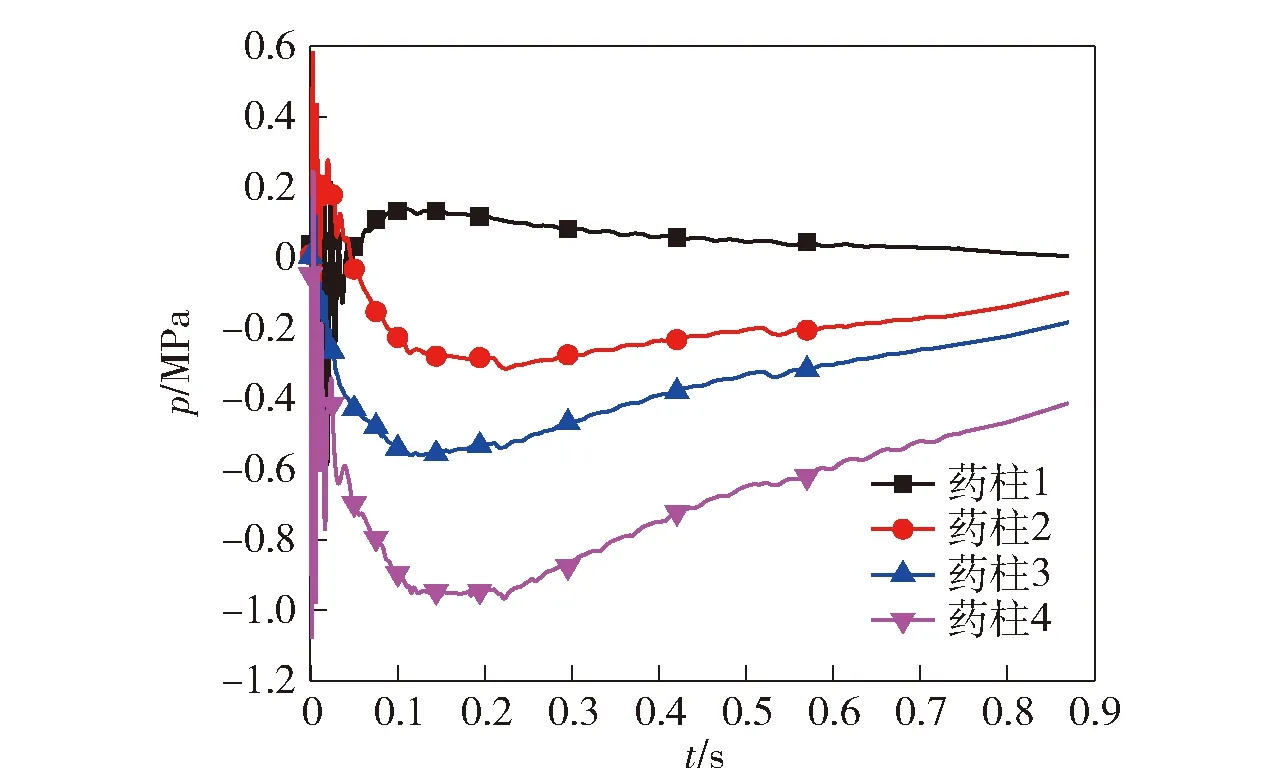
图9 药柱内外压强差Fig.9 Pressure differences inside and outside grain

图10 前后药柱中部纵切面的压强分布(150 ms)Fig.10 Distribution of pressure on middle part longitudinal section of front and rear grains (150 ms)
读取图9中的计算数据可知,在150 ms时各药柱内外燃面基本处于最大压强差值,药柱1压强差0.13 MPa外燃面比内燃面压强高0.9%,药柱2压强差0.28 MPa内燃面比外燃面压强高2%,药柱3压强差0.55 MPa内燃面比外燃面压强高3.9%,药柱4压强差0.96 MPa内燃面比外燃面压强高8%. 由图10压强分布图可以看出,药柱1、药柱2、药柱3的外燃面压强和燃烧室前部压强都相同,药柱4的外燃面压强和燃烧室后部压强相同。在燃烧室高压强部分药柱内外压差小,最高不超过0.55 MPa;在燃烧室低压部分药柱内外压差比较大,为0.96 MPa.
根据文献[19]得到双基推进剂剪切许用应力,再根据本文所用推进剂的具体尺寸,计算得出试验用推进剂剪切许用压强大约为3.8 MPa. 由此表明药柱1、药柱2、药柱3、药柱4的压强差均在可承受之内。
2.3 侵蚀比模型计算结果与试验对比分析
图11所示为静态试验平台现场图。试验温度大约15 ℃,为了避免地面效应对尾流场的影响,导致对燃烧室内的压强有所影响,将试验装置竖直向上放置。

图11 静态试验平台现场图Fig.11 Site diagram of static test platform
图12所示分别为燃烧室前部、中部、后部监测点的无量纲标准化压强- 时间曲线计算结果与试验结果对比。

图12 燃烧室前部、中部、后部监测点的无量纲标准化压强- 时间曲线计算结果与试验结果对比Fig.12 Dimensionless standardizing pressure-time curves at monitoring points on the front, middle and rear parts of combustion chamber from numerical and experimental results
由图12(a)可知:燃烧室前部计算压强上升和下降阶段与试验结果吻合较好,在平衡压强阶段计算考虑的推进剂同时燃烧,试验中推进剂随着点火逐渐燃烧;在平衡压强阶段开始计算压强比试验高,下降梯度比试验快,推进剂燃完时计算压强比试验低。由图12(b)可知:燃烧室中部试验压力上升一段之后下降再上升,这是因为试验中部点火压力不够所造成的;在推进剂开始燃烧之后压力才上升到最大,如果中部点火压力正常则试验曲线和计算曲线的趋势应该吻合较好。由图12(c)可知:燃烧室后部计算是考虑后级推进剂一开始就全面燃烧,试验是随着点火逐渐燃烧;计算结果上升梯度比试验快,最大压力高,到平衡压力和燃烧结束阶段计算与试验结果吻合较好。3个监测点的计算结果与试验结果的总冲量(压强对时间的积分)一致性很好。
3 结论
本文建立了带侵蚀燃烧效应的阶梯多根装药火箭发动机的全三维内流场,针对其工作过程进行了数值模拟。通过对数值计算结果分析以及与试验对比,得到主要结论如下:
1)对于侵蚀比和平均侵蚀比两种模型,最大压强差不超过3%,在平衡压强段后基本一致。表明两种模型都可用于大长径比阶梯装药结构火箭发动机的计算,为火箭发动机内弹道计算提供参考依据。
2)侵蚀比模型内流场的最高压强不超过20 MPa,在发动机工作过程中药柱没有出现明显的侵蚀燃烧喇叭型,两级装药基本同时燃完。最大压强在燃烧室可承受范围,同时尽量避免了侵蚀燃烧的影响,表明装药结构设计安全、合理。
3)在燃烧室前部高压区药柱内外压差最大不超过3.9%和0.55 MPa,在燃烧室后部低压区药柱内外压差最大不超过8%和0.96 MPa,在150~200 ms时压强差持续较高、然后越来越小,压强差在药柱可承受范围之内。
4)根据压强- 时间计算与试验曲线的对比可知,每个监测点的计算与试验的总冲量一致性较好,计算曲线与试验曲线吻合较好。证明了计算模型和结果的准确性,表明本文两个计算模型都可用在类似装药结构的固体火箭发动机计算中,能够为复杂结构的固体火箭发动机侵蚀燃烧的研究提供参考依据。

