发射筒易碎前盖开盖过程的流体与固体耦合仿真方法
张宝振, 王汉平, 窦建中, 程梦文
(北京理工大学 宇航学院, 北京 100081)
0 引言
易碎盖技术能极大提升导弹作战的响应速度,同时兼具质量轻、免维护、可靠性高等优点,是导弹贮运发射箱研制中的关键技术。当发动机产生的冲击波或高压燃气冲击后盖时,将会产生扰动波[1],扰动波向前盖方向传播,可用于开启易碎前盖,从而为导弹的发射出筒打开通道;文献[2-3]利用计算流体力学(CFD)仿真和实验手段对易碎盖开盖过程进行研究,验证了上述开盖机制;党海燕等[4]探讨了易碎后盖开盖压力对易碎前盖的影响,仿真表明,易碎前盖的开盖压力设计应依据易碎后盖的开盖压力进行合理匹配;牛钰森等[5]利用动网格技术,将后盖裂片运动过程与流场耦合,对整个开盖过程进行仿真分析,结果表明,相比于非耦合工况,流体与固体耦合工况的计算结果与实验数据更接近;靖建全等[6]采用动网格技术模拟后盖脱落运动过程,并利用分区边界的类型变化来模拟后盖破裂过程,结果显示,后盖运动和破碎过程对发射箱内扰动波的产生和传递有重要影响;文献[7-8]利用ABAQUS软件中耦合的欧拉- 拉格朗日(CEL)算法对地面气动载荷作用下的大型整流罩分离过程进行模拟,发现基于CEL算法的仿真结果与实验数据吻合较好;王懿等[9]基于CEL算法建立了抛锚入泥深度的数值模型,仿真研究了土壤不排水抗剪强度、抛锚速度、锚尺寸等参数对船舶抛锚入泥深度的影响;徐文杰[10]则利用CEL算法对滑坡涌浪这种复杂的流体与固体耦合问题进行仿真分析,且仿真结果与实验数据具有较好的吻合度。由此可见,CEL算法在解决低速流动条件下流体与固体耦合问题具有广泛的适用性。
国内对易碎盖开裂过程的研究主要是基于结构的断裂力学[11-12],而未考虑流场与易碎盖碎片运动过程的耦合效应;对易碎盖开盖过程中流体与固体耦合问题的研究,则多采用CFD中的动网格技术,却未细致引入易碎盖结构的开裂过程,且研究对象也均为易碎后盖。有鉴于此,本文构建了一种针对易碎前盖与箱内、箱外流场相耦合的仿真模型,将CFD流场仿真压强作为输入条件,利用扩展开发的易碎盖材料混凝土塑性损伤(CDP)本构模型,对易碎前盖开盖过程的流体与固体耦合问题进行了仿真研究。这种将CEL算法应用于耦合面变拓扑的易碎前盖开裂仿真尚属先例。仿真结果表明:扩展开发的CDP本构模型可用于易碎盖的结构设计和强度优化;CEL算法能有效解决易碎前盖的扰动波开盖过程的流体与固体耦合问题,且能细致捕捉易碎盖碎片上的载荷变化特性,可为精准控制易碎盖的冲破力[13]提供数据支撑。
1 CEL算法
CEL算法最早由Noh[14]提出,其兼具拉格朗日方法和纯欧拉方法的优势,能够有效克服单元畸变和实现高精度的界面捕捉。该算法所使用的结构网格和流体网格各自独立,两域的网格可相互重叠,且对两套节点的对应与否并无特别要求。CEL算法能在流体域和固体域之间进行载荷、位移、速度等参数信息的实时传递,不需要复杂繁琐的人工干预。因此,CEL算法在模拟流体流动、液面晃动、流体与固体耦合等大变形问题时,具有强大的优势。
CEL算法的控制方程由连续方程、动量守恒方程和能量守恒方程组成,控制方程需在欧拉坐标下进行时间积分。扰动波开盖涉及发射箱内外的环境,故需附加理想气体的状态方程:
p+pa=ρR(T-Tz),
(1)
式中:p为气体压强;pa为环境压强;ρ为气体密度;R为气体常数;T为气体温度;Tz为绝对温度的0 K值。
ABAQUS软件中的CEL算法采用罚函数耦合算法[15]来实现流体域和结构域之间的耦合。计算过程中,通过追踪固体节点对流体欧拉材料界面的贯穿深度δ来确定界面贯穿力的大小。如果发生固体节点对流体材料界面的贯穿,界面力就会分布到流体欧拉材料的锚定点上,如图1所示。界面力的大小F与贯穿深度δ呈正比:

图1 罚函数耦合算法Fig.1 Penalty function coupling algorithm
F=kiδ,
(2)
式中:ki为第i个单元的罚刚度系数,其值取决于拉格朗日和欧拉材料特性。
2 易碎前盖材料的本构模型和校验
2.1 易碎前盖材料实验及本构模型的选择
在易碎前盖的扰动波开盖过程中,前盖承受的是冲击载荷,材料的应变强化以及应变率效应影响十分明显,因此,需要测试不同应变率条件下的拟静态及动态拉伸、压缩力学性能[16]。拟静态拉伸、压缩实验试件按国家标准GB 9641—1988《硬质泡沫塑料拉伸性能试验方法》、GB 8813—1988《硬质泡沫塑料压缩性能试验方法》予以制备,实验在电子万能实验机完成;动态拉伸、压缩实验试件由航天科工集团第10研究院航天天马公司提供,实验在霍普金森拉杆和霍普金森杆压杆实验装置上完成。拟静态、动态实验应变率数据如表1所示。

表1 实验类型及数据Tab.1 Test types and test data
限于篇幅,在此仅列出应变率为1.0的拟静态拉伸、压缩实验的应力- 应变曲线,如图2所示。从图2中可以发现:易碎前盖的材料属于硬脆性材料,单轴拉伸行为表现准脆性,单轴压缩行为表现先硬化、后软化,非常类似于 CDP本构模型。因此,可考虑用扩展开发了断裂失效的CDP本构模型来表征其材料的力学特性,该模型中的参数可根据实验数据予以拟合。

图2 拟静态拉伸和压缩的工程应力- 应变曲线Fig.2 Engineering stress-strain curves of quasi-static tension and compressed case
2.2 易碎盖材料本构模型的扩展开发及验证
由于CDP本构模型无失效单元的删除功能,为了附加对失效单元的标记及删除操作,扩展开发了用户子程序VUSDFLD.

E=(1-di)E0,
(3)
式中:di中的i分别对应下标t和c,分别表示拉伸、压缩,dt、dc分别为拉伸和压缩塑性损伤因子,di的取值范围为0~1,0表示材料未出现损伤,1表示材料强度完全丧失。
由CDP本构模型受拉、受压的应力- 应变关系和张劲等[17]基于规范混凝土的应力- 应变提出公式,可建立开裂应变与受拉损伤的联系、非弹性应变与受压损伤的联系,计算公式为
(4)
(5)

CDP本构模型在三维多轴状态下的应力- 应变关系可通过损伤弹性方程表示:
(6)

通过σ计算静水压力以标记积分点的拉伸、压缩状态,并将仿真计算的累积损伤因子di与材料实验拟合出的损伤因子进行比较,若计算的损伤因子大于材料失效的损伤因子,则将材料标记为失效,并完成对单元的删除。
在ABAQUS软件中分别进行材料拟静态拉伸、压缩状态和动态拉伸状态的仿真,将仿真结果和实验结果对比,以此来对开发的CDP本构模型进行校验,结果如图3和图4所示。结果表明:扩展开发的CDP本构模型能够较好地吻合试件的失效状态,且静态拉压载荷- 变形量数据也吻合较好。其中,拉伸载荷的差异在于材料的拉伸、压缩弹性模量不一致,即材料的压缩弹性模量大于拉伸弹性模量,而仿真是按压缩弹性模量来赋予材料弹性模量属性的。压缩的软化段仿真载荷值小于实验值,其原因在于:仿真模型中单元失效后会被删除,且未设置单元失效后断裂界面与单元表面接触,因此仿真模型的承载能力有所降低。

图3 实验和仿真破坏形态Fig.3 Experimental and simulated failure modes

图4 单轴拉伸和压缩载荷- 变形量的实验数据与仿真结果对比Fig.4 Comparison of simulated results and experimental data of uniaxial tension/compression loading and deformation
3 基于CFD方法的流场仿真
3.1 仿真模型
考虑到发射筒和导弹的结构特征,将流场仿真模型简化为二维轴对称模型,计算域由弹体、喷管及发射筒前、后盖以及后盖外的部分区域组成。为监测流场状态参数的变化情况和扰动波的传播特性,在发射箱内距喷管出口0~5 m处的筒壁、筒与弹之间以及前盖上设置压强、温度监测点。模型计算域网格均采用结构化网格,网格总数为32万个。仿真模型的计算域及各监测点的分布如图5所示。

图5 模型计算域及监测点分布Fig.5 Computational domain and monitoring point distribution
3.2 条件设定
导弹发动机燃气参数如表2所示。

表2 燃气参数表Tab.2 Gas parameters
依据总体要求,破片压强为3 MPa,发射箱内预先充气10 kPa,故在初始参数设置时,将导弹、发射筒间的气体压强设置为10 kPa. 发动机高压室以外的计算域初始参数为静止大气参数:p0=101 325 Pa,T0=300 K. 发动机燃烧室的总温Tt=3 000 K,总压为导弹发动机燃烧室的总压时间历程,如图6所示。

图6 燃烧室总压时程曲线Fig.6 Curve of total pressure over time
喷管出口边界条件为压力入口。后易碎盖开启前,其边界条件为无滑移绝热壁面;开启后,其边界条件为压力出口。为获取后盖在不同时刻开启时,前盖在反射扰动波作用下所能达到的载荷状态,因此将前盖设定为壁面。
通过设定后盖的开启时间来控制后盖边界条件的切换,仿真设定的后盖开启时间分别为1 ms、2 ms、3 ms、4 ms、5 ms、6 ms和7 ms,共计7种工况。按前述设定参数,对以上7种工况进行仿真,探究发射过程中的反射扰动波、传播特性,以及前易碎前盖的受载特性。
4 基于CEL算法的建模及分析
采用CEL算法来处理扰动波开盖的流体与固体耦合问题,需要将CFD方法得到的压强时程用作CEL模型的入口条件。而在建立CEL模型之前,需将CFD模型和ABAQUS欧拉模型的箱壁上1号~5号监测点处的压强时程曲线进行对比,以验证两方法计算出的压力波在幅值、传播速度上的一致性,这是进行流体与固体耦合仿真的基础。
4.1 欧拉单元仿真分析及校验
4.1.1 基于欧拉方法的流场建模及仿真
由于发射筒的结构特性,可选取结构的1/6进行建模。建立发射箱内距离喷管出口1 m处(即1号监测点截面)至前盖的欧拉模型,并建立与CFD模型位置相匹配的监测点。所有网格均为EC3D8R单元,节点数250 835个,单元数230 232个。欧拉模型的网格模型及监测点分布如图7所示。

图7 欧拉模型的网格及监测点分布Fig.7 Grid and monitoring points distribution of Eulerian model
选用理想气体状态方程,欧拉材料的定义与CFD方法中定义的气体属性一致。距离喷管出口1 m截面处设置为压强入口,压强幅值曲线按CFD仿真提供的监测点1处的压强时程曲线予以设置;除距离喷管出口1 m截面处,其余外部边界均设置为绝热无滑移边界条件。由于欧拉仿真验证不需拉格朗日单元,所以初始条件下,欧拉体积分数全部为1.
选择ABAQUS显示动力学求解器,仿真时间为0.025 s. 按上述设定参数,对7种工况进行仿真,获取各监测点处的压强时程曲线。
4.1.2 欧拉方法与CFD方法的仿真对比
根据CFD方法和欧拉方法的仿真计算,得到各监测点处的压强时程曲线。限于篇幅,仅对后盖开启时间为6 ms这一工况,将两种方法中筒壁上1号~5号监测点、前盖3号监测点的压强时程曲线对比分析,分别如图8(a)和图8(b)所示。
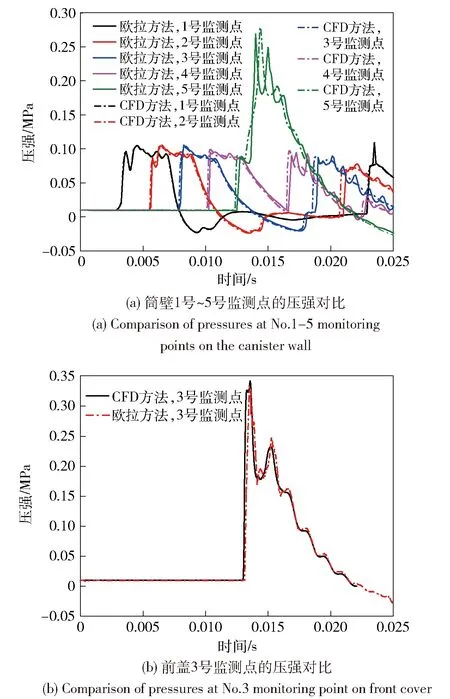
图8 筒壁上各监测点和前盖3号监测点的压强时程曲线(CFD方法与欧拉方法对比)Fig.8 Pressures at monitoring points on the canister wall and monitoring point 3 on the front cover (CFD method vs. Eulerian method)
从图8中可以看出:欧拉方法与CFD方法得到的箱壁、前盖3号监测点的压强时程曲线基本重合,可见两方法得到的压力扰动波的幅值、传播速度、反射特性吻合较好,这是进行压力波开盖流体与固体耦合分析的有力支撑;各监测点均出现压强二次峰值,这是因前盖对压力波的反射而形成。图8中同一监测点处的压力波在传播速度、压强幅值方面存在微小差别,这是由欧拉方法和CFD方法确立的监测点位置不完全重合导致的,即CFD方法是根据距离设置的监测点,而欧拉方法的监测点位置是根据网格节点予以定义的。
本设计是基于单一景点深度开发的专门性的游客服务的手机APP。本设计专注于单一景点开发,因此景点的信息覆盖全面,没有冗杂信息干扰,目的性明确,垂直服务于景点旅游的游客。本设计的意义在于旅游景区为游客提供更好的服务,为用户提供更好的指引。同时游客能够通过APP随时随地了解某一景区的最新动态,有利于自己选择合适的时间出游,并且能够快速地满足酒店、旅游社以及旅客三方面的需求[3]。
4.2 易碎前盖的流体与固体耦合仿真
4.2.1 CEL模型的建立
考虑到发射筒和易碎盖的结构特征,可用其1/6循环对称的结构进行建模计算。易碎前盖的1/6结构示意图如图9所示。

图9 易碎前盖的1/6结构示意图Fig.9 1/6 schematic diagram of fragile front cover
CEL模型建模与欧拉模型基本一致,不同之处为:前盖网格为拉格朗日单元,需将前盖和发射筒的欧拉域进行装配。边界条件除绝热无滑移和对称边界外,需设置欧拉边界:自由流入和无反射流出;还需对拉格朗日单元附近的欧拉单元进行局部加密,以保证耦合区域的网格密度,同时避免计算量的过分增加。
CEL模型中易碎前盖的拉格朗日网格(C3D8R)为61 952个,流场域的欧拉网格(EC3D8R)为334 635个,网格模型如图10所示。

图10 CEL模型的网格及监测点分布Fig.10 Grid and monitoring points distribution of CEL model
4.2.2 CEL模型仿真结果分析
经过仿真计算和数据处理,得到CEL模型监测点处的压强时程曲线。限于篇幅,仅对后盖开启时间为6 ms这一工况,将CEL算法与CFD方法的结果进行对比分析,如图11所示。
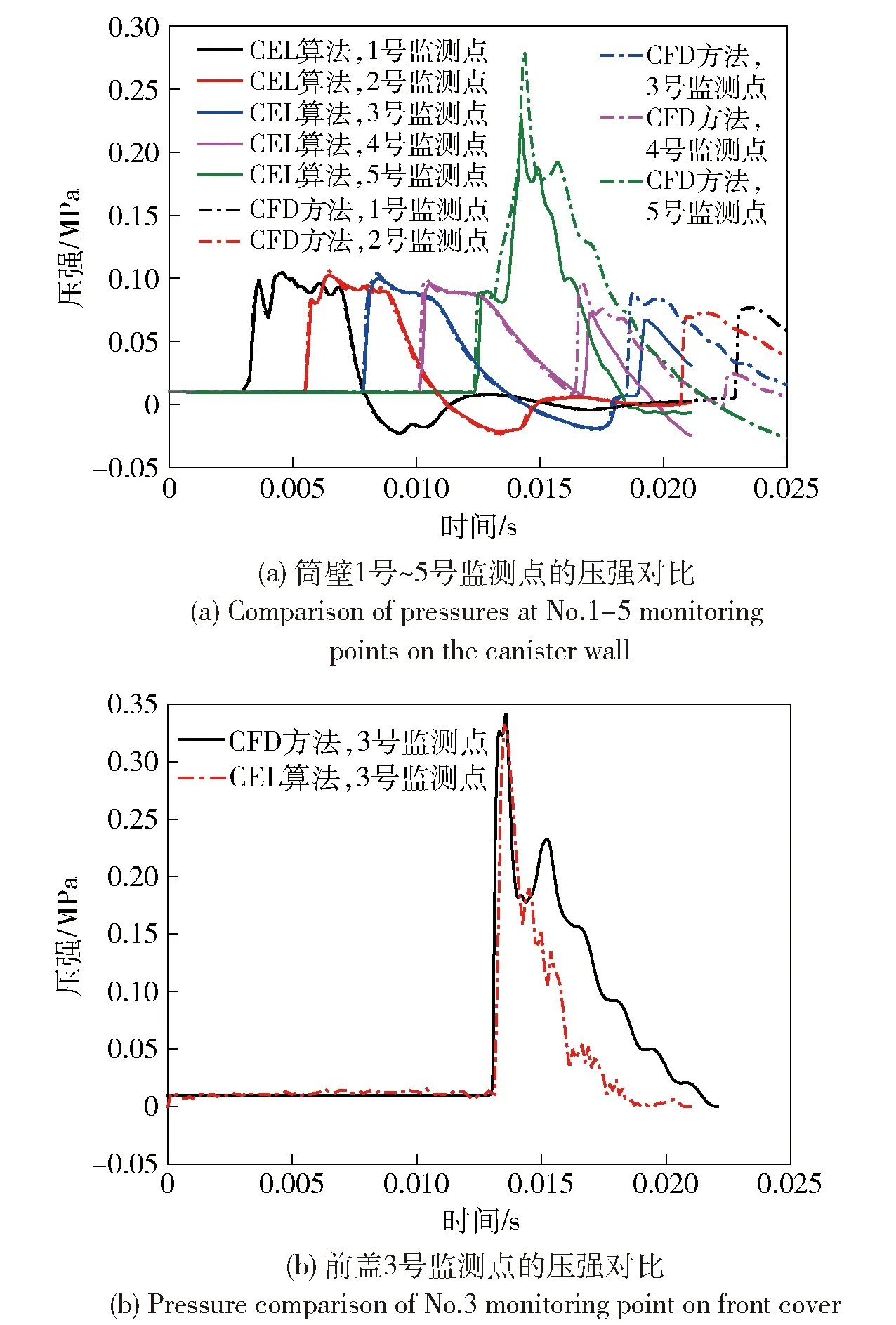
图11 箱壁上各监测点和前盖监测点3的压强时程对比(CFD方法与CEL算法对比)Fig.11 Pressure curves of monitoring points on the canister wall and No.3 point on the front cover (CFD method vs. CEL algorithm)
CEL模型中易碎前盖内表面接触压力云图如图12所示,其中图12(a)~图12(j)为选取的特征较为明显的压力云图,对应的时刻依次为:12.875 ms、13.0 ms、13.5 ms、15.0 ms、15.5 ms、16.0 ms、16.5 ms、17.0 ms、17.5 ms、18.0 ms. 从图12中可以看出:12.875 ms是反射压力波传递到前盖的第一个输出步,此时,易碎前盖内表面并无压力变化;在13.0 ms时,压力波已传递到前盖,但只是先传到前盖的法兰处;再经过4个计算步,在13.5 ms时,压力波完全作用到盖上,压力波在不同时刻到达前盖各个位置,并且向更靠近中轴线的方向汇聚,所以在盖的中间处会有明显的压强增大,这有利于前盖的开启;压力波持续一段时间后,在15.5 ms时,前盖完全沿预制沟槽开启,且开裂效果良好。如图13所示,易碎前盖已完全碎裂并飞离发射筒。之后,易碎盖碎片在压力波冲击下进一步运动。

图12 易碎前盖开裂过程的内表面压力云图Fig.12 Pressure nephogram of inner surface of fragile front cover

图13 前易碎盖完全破裂Fig.13 Completely broken fragile front cover
5 结论
本文构建了考虑易碎前盖与压力波交互作用的CEL流体与固体耦合模型,利用扩展开发的易碎前盖材料的CDP本构模型,在辅以CFD仿真数据作为压力边界的条件下,对易碎前盖的压力波开盖过程进行了流体与固体耦合仿真分析。根据仿真分析,可得出以下主要结论:
1) 扩展开发后的CDP本构模型能有效模拟材料的失效以及失效单元的删除,也能很好复现材料实验和产品实验的结果,适合于易碎前盖的本构模拟应用。
2) 以CFD仿真结果作为欧拉模型的边界条件,对压力波的传播、反射特性进行了对比仿真验证。结果表明:CFD方法、欧拉方法的压力波强度、传播速度及其反射特性吻合较好,欧拉方法能较好地模拟压力波的传播及反射特性,这说明基于有限元的欧拉方法在模拟压力波的传播、反射方面具有匹配CFD的模拟精度。
3) 将CFD仿真结果作为CEL流体与固体耦合模型的边界条件,开展易碎前盖的开裂过程仿真,在压力波的自由传播、反射特性及其与易碎前盖接触耦合方面,CEL模型更符合实际状态。采用CEL算法能够较好地解决耦合面变拓扑的易碎前盖开裂的仿真问题,这种将CFD与CEL相结合的仿真方法为易碎前盖的压力波开盖流体与固体耦合分析提供了一种可信的新方法,为工程中易碎盖的设计和优化提供更优良的解决方案。

