基于LTE信号外辐射源雷达的同频干扰抑制算法
邵晓浪, 胡泰洋, 肖泽龙, 卫永平, 王华
(1.南京理工大学 电子工程与光电技术学院, 江苏 南京 210094;2.淮海工业集团有限公司, 山西 长治 046012; 3.中国运载火箭技术研究院 研究发展中心, 北京 100076)
0 引言
LTE信号为第4代移动通信技术所使用的无线通信信号,是一种全世界范围内广泛分布的通信信号。相对于传统的机会外辐射源信号,LTE信号具有更高的距离和速度分辨率[1]。同时,LTE信号发射基站资源非常丰富,有着天然的网络协同探测优势,因此基于LTE信号的外辐射源雷达是一个重要的研究方向[2]。
不同于广播、电视信号发射站发射不同频段的信号,基于LTE信号的外辐射源雷达系统,由于其发射基站采用蜂窝式布站,且不同的发射基站共用同一个频段,所以接收时无法通过频域滤波的方式加以区分,主通道接收到的信号不仅包含参考天线所指向的主基站的直达波和多径杂波,还会包含其他同频基站的直达波和多径杂波[3],并且由于其布站密集,同频干扰的问题成为了影响LTE信号外辐射源雷达探测性能的重要因素。
不同LTE基站发射的信号不同,所以仅利用指向主基站的参考通道信号,只能对消监测通道中来自主基站的直达波和多径杂波干扰,无法对消其他同频基站的杂波干扰。文献[4]提出了一种级联相消的同频干扰抑制算法,在先验获得同频基站信息前提下可以有效地对消同频干扰。文献[5]研究了一种空域自适应滤波的方法来抑制同频干扰,该方法技术成熟、实现简单,在目标信号波达角(DOA)确定情况下,具备良好的干扰抑制效果。文献[6]将独立分量分析(ICA)方法用于同频干扰抑制,将各辐射源直达波及其多径、目标回波都视作不同的源信号,使用基于瞬时混合模型的快速ICA(Fast ICA)算法依据源信号的统计独立性与非高斯性实现时域分离,然后进行后续对消,解决了文献[3]中对同频干扰基站先验信息的依赖。但是由于不同基站发射的LTE信号经过编码、调制,映射到物理层之后呈现高斯分布特性,不满足Fast ICA算法的使用条件,因此不适用于LTE信号。针对于文献[6]的问题,文献[7-9]进一步提出了基于卷积混合模型的盲源分离算法分离同频基站信号,然后用分离的信号作为参考信号进行级联相消,实现同频干扰抑制,能够适用于多个高斯分布的LTE信号。
上述算法往往采用对LTE同频基站干扰进行直接抑制或对消的策略,基于盲源分离结合级联相消算法是其中的主流。在这类算法中,级联的相消器个数取决于同频干扰基站的数量,如果同频干扰基站的数量过多,则系统的复杂度和实时性难以接受。
由于目标信号和对消信号并不是完全正交的,因此在不断的对消过程中会降低信号的信噪比(SNR)。此外,级联相消效果受所选择的对消算法和设置的参数影响,干扰对消效果有限。
本文利用阵列信号处理中阵列流型矩阵和混合矩阵结构一致这一特点,首先采用m-Capon算法估计未知信号数的阵列流型矩阵[10],实现信号分离。然后将分离的信号并行进行互模糊相关处理,最后利用LTE目标信号、同频干扰信号和参考通道主基站信号三者在距离- 多普勒域上的差异特征,分辨干扰和目标,间接抑制了同频基站干扰的影响。相比级联相消类算法,本文算法在信号分离后无需后续的级联对消过程,降低系统复杂度,并且具有更优的干扰抑制效果,虽然需要进行多次互模糊相关,但是通过并行处理,并不影响整个系统的实时性。得益于欠定DOA估计算法[11-12]和信源恢复算法[13-14],本文算法框架同样适用于欠定情况下的同频干扰抑制。
1 LTE外辐射源信号模型
LTE外辐射源雷达主通道接收到目标反射信号、主基站直达波信号和多径信号以及多个同频发射基站的直达波和多径信号,主通道第i个阵元接收信号可表示为
(1)
式中:K为同频基站数目;Nk(k≠0)为各个同频基站信号的多径数,N0为主基站的多径数;ai(θk,n)为第i个阵元对应的不同到达角θk,n的控制量,θk,n为第k个基站第n个多径信号的到达方向角;sk(t-τk,n)(k≠0)为第k个同频基站中直达波和多径信号,τk,n为第k个基站第n个多径信号的时延,s0(t-τ0,n)为对应主通道接收信号中主基站的直达波和多径信号,τ0,n为主基站第n个多径信号的时延;NT为目标总数;ai(θq)为第i个阵元对应不同到达角θq的控制量,θq为第q个目标回波信号的到达方向角;s0(t-τq)ej2πfqt为主基站的目标回波信号,fq和τq分别为目标的多普勒频率和时延;wi(t)为第i个接收阵元的噪声。值得注意的是,在实际情况中还存在各种同频基站的目标回波信号,由于其能量很小,将其视为噪声的一部分[7]。
考虑接收天线采用M个阵元的均匀线性阵列(ULA),如图1所示。图1中sn(t)为第n个入射信源,θn为第n个信号的到达方向角,d为相邻两个阵元的间距。
LTE外辐射源雷达接收的目标回波、主/同频基站的直达波和多径信号视为不同的信源,设总的信源数目为N,(1)式可以写为
xi(t)=AiS(t)+wi(t),
(2)
式中:Ai=[ai(θ0,0),…,ai(θk,n),ai(θ0),…,ai(θq)],为了便于表述,定义源信号入射角度集[θ0,0,…,θk,n,θ0,…,θq][θ0,θ1,…,θN],即Ai=[ai(θ1),…,ai(θn),…,ai(θN)],其中ai(θn)=exp (-j2πfcτi,n),τi,n为第i个阵元第n个入射信源的时延,分别为载波波长和载波频率;S(t)为(1)式中主基站直达波及多径信号、同频基站直达波和多径信号以及目标回波信号的组合。
接收信号可表示成矩阵形式
X(t)=AS(t)+W(t),
(3)
式中:X(t)=[x1(t),x2(t),…,xM(t)]T;A=[A0,A1,…,AM]T;W(t)为噪声信号矢量,W(t)=[w1(t),w2(t),…,wN(t)]T.A∈M×N是复值混合矩阵,可以表示为
(4)
2 同频干扰抑制流程
本文利用不同LTE基站信号互相关性较弱这一特征,首先对主通道接收的信号进行m-Capon谱估计,计算混合矩阵,采用最小二乘法实现干扰信号和目标信号分离。然后将分离后的信号与主通道提纯后的参考信号[15-16]并行进行互模糊相关,根据干扰和目标信号的互模糊相关差异制定判决策略,识别目标。同频干扰抑制流程如图2所示。
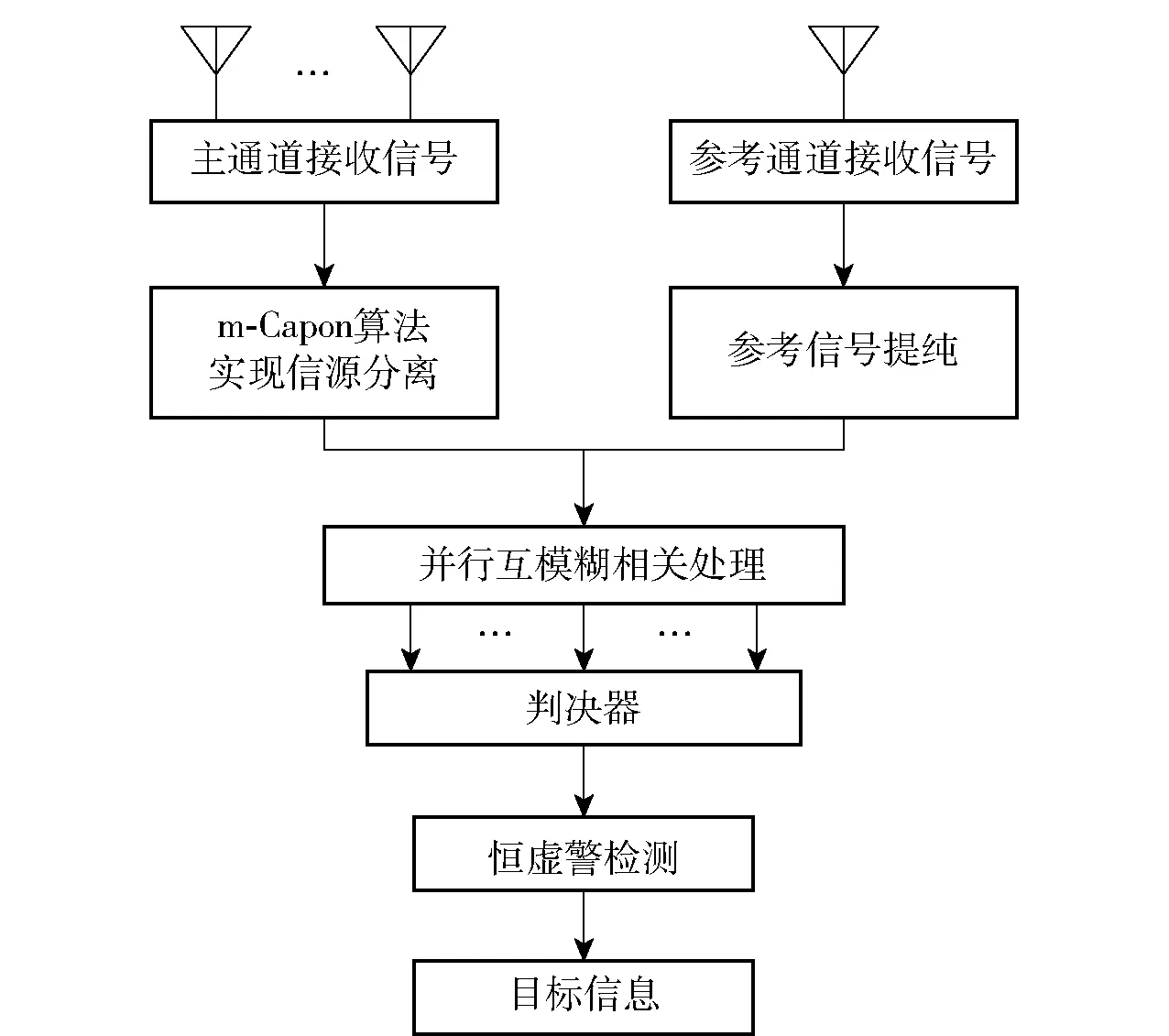
图2 同频干扰抑制流程Fig.2 Co-channel interference suppression process
2.1 基于m-Capon谱估计的信源分离
盲源分离算法核心的任务就是完成混合矩阵A的估计,在阵列信号处理中,混合矩阵和阵列流型矩阵结构一致,因此只要完成了对入射信号角度θn的估计,根据阵列结构可以计算得到对应θn的导向矢量,混合矩阵A就是由所有信号的导向矢量组成。
m-Capon谱估计算法是一种信源数未知DOA估计算法,该算法不需要预判信源个数和进行特征值分解,同时在时变环境下,针对快拍数较小的情况,仍然保持较高的角度分辨力,综合了Capon法和多信号分类(MUSIC)算法的优点[10]。LTE信号在时域上表示为多个正交子载波的叠加,当子载波个数达到一定程度后,根据中心极限定理,LTE信号的波形将是一个高斯随机过程,不同延时之间的相关性较弱,因此在本文中不考虑多径信号相关性引起的缺秩现象。
接收信号矩阵X自相关矩阵RX的特征值分解为
(5)
式中:(·)H表示共轭转置;RS为信号的协方差矩阵;σ2为噪声功率;I为单位矩阵;ΣS为主特征值矩阵;VS、VW分别为信号子空间和噪声子空间。
进一步推导,可得
(6)
式中:m为任意整数;由于σ2/λi是小于1的数,λi是对应信号子空间的特征值,因此当m趋向于无穷大时,(6)式趋向于噪声子空间,即
(7)
因此无需先验地知道信源个数和特征值分解即可得到噪声子空间。(7)式表明m趋向无穷时收敛到噪声子空间,事实上选取很小的整数就能达到很好的性能,在本文中m=3.
结合(7)式和传统的Capon谱估计函数,m-Capon空间谱函数为
(8)
式中:a(θ)表示来波信号DOA为θ值的导向失量;X是对接收数据自相关矩阵RX通过L次快拍数据估计得到,
(9)
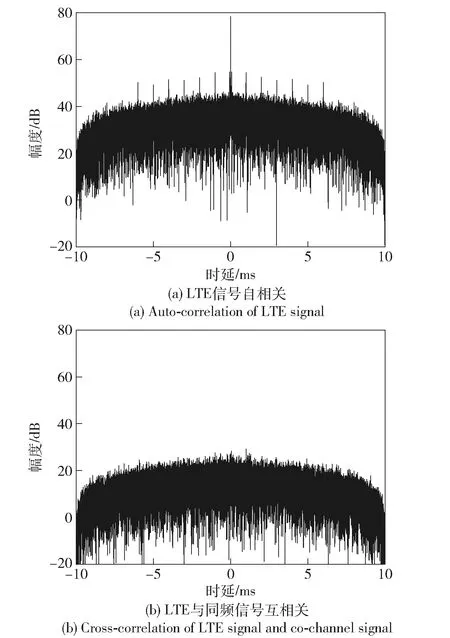
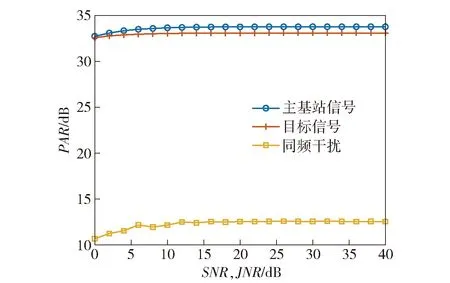
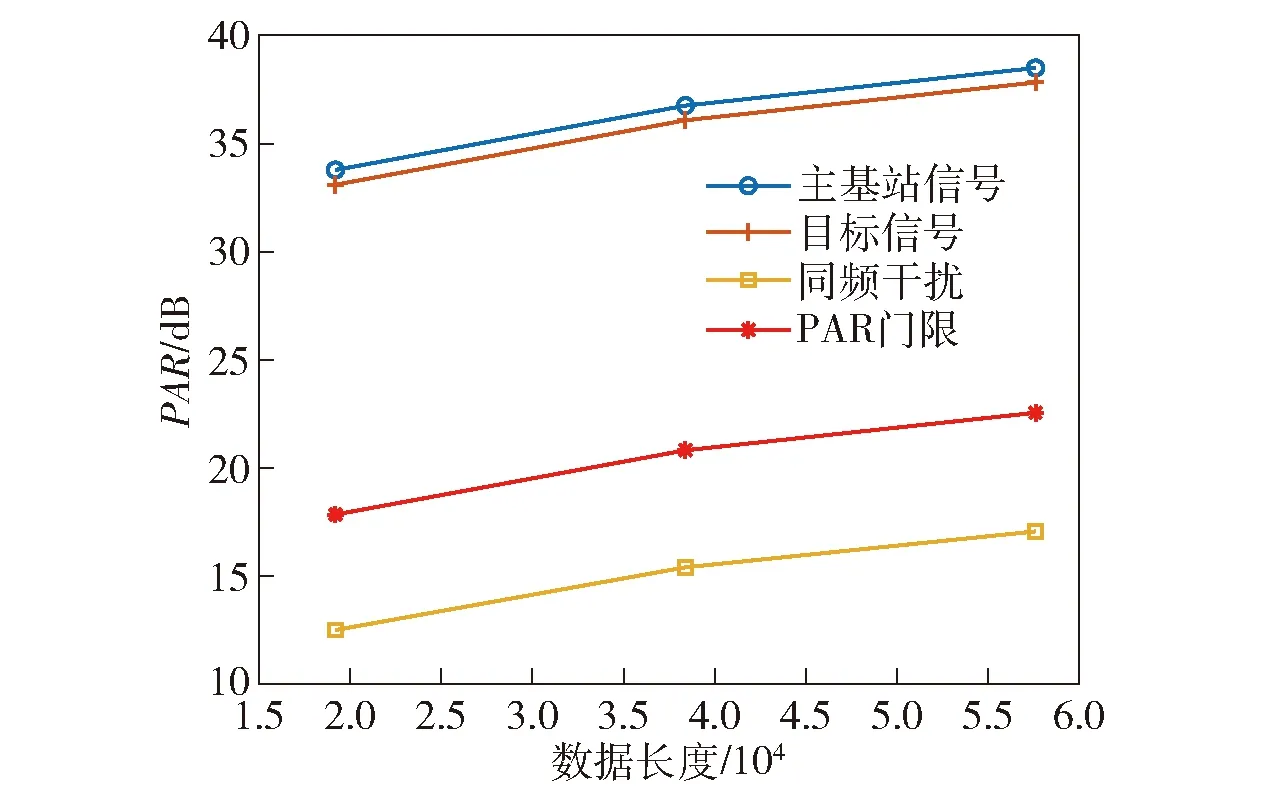
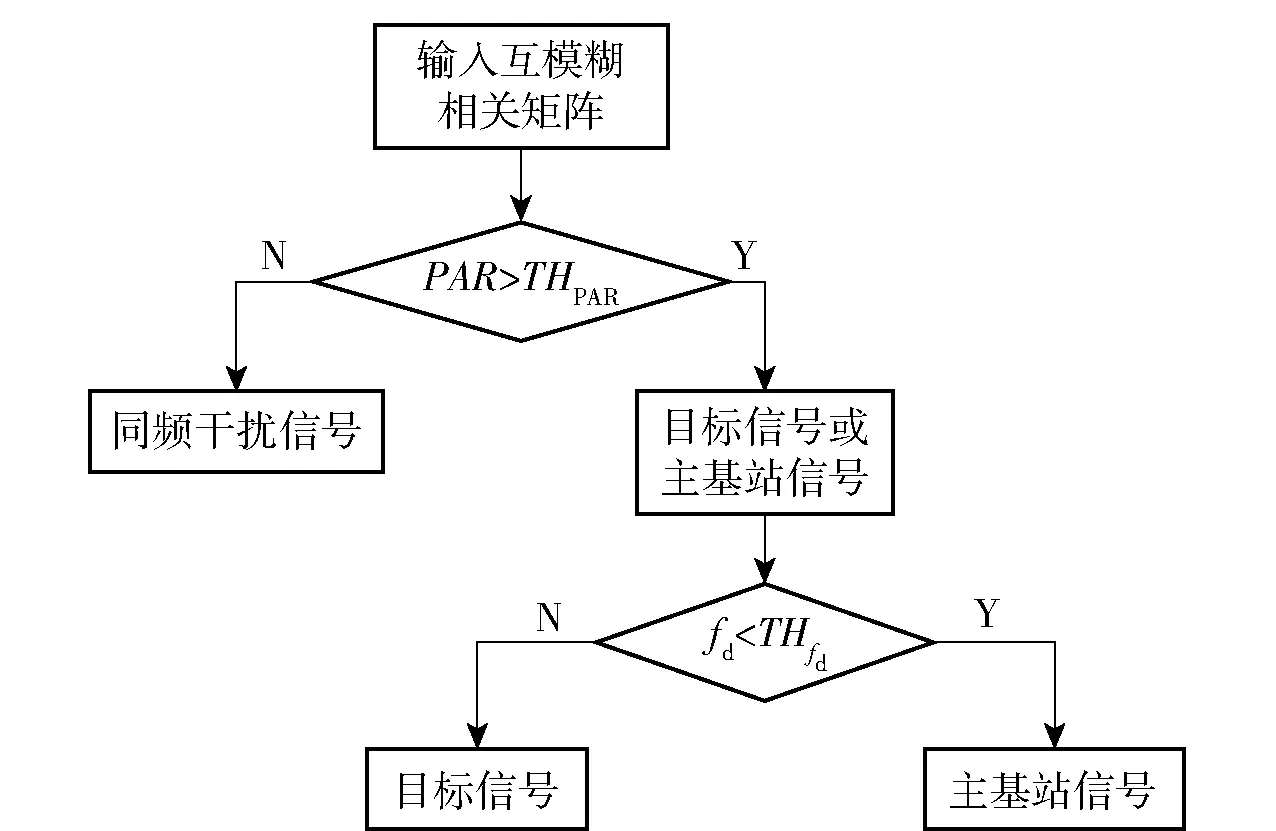
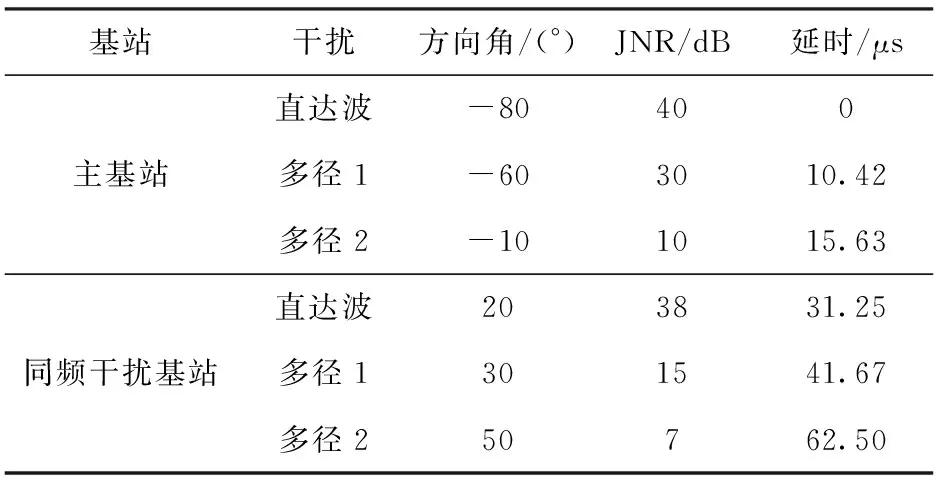
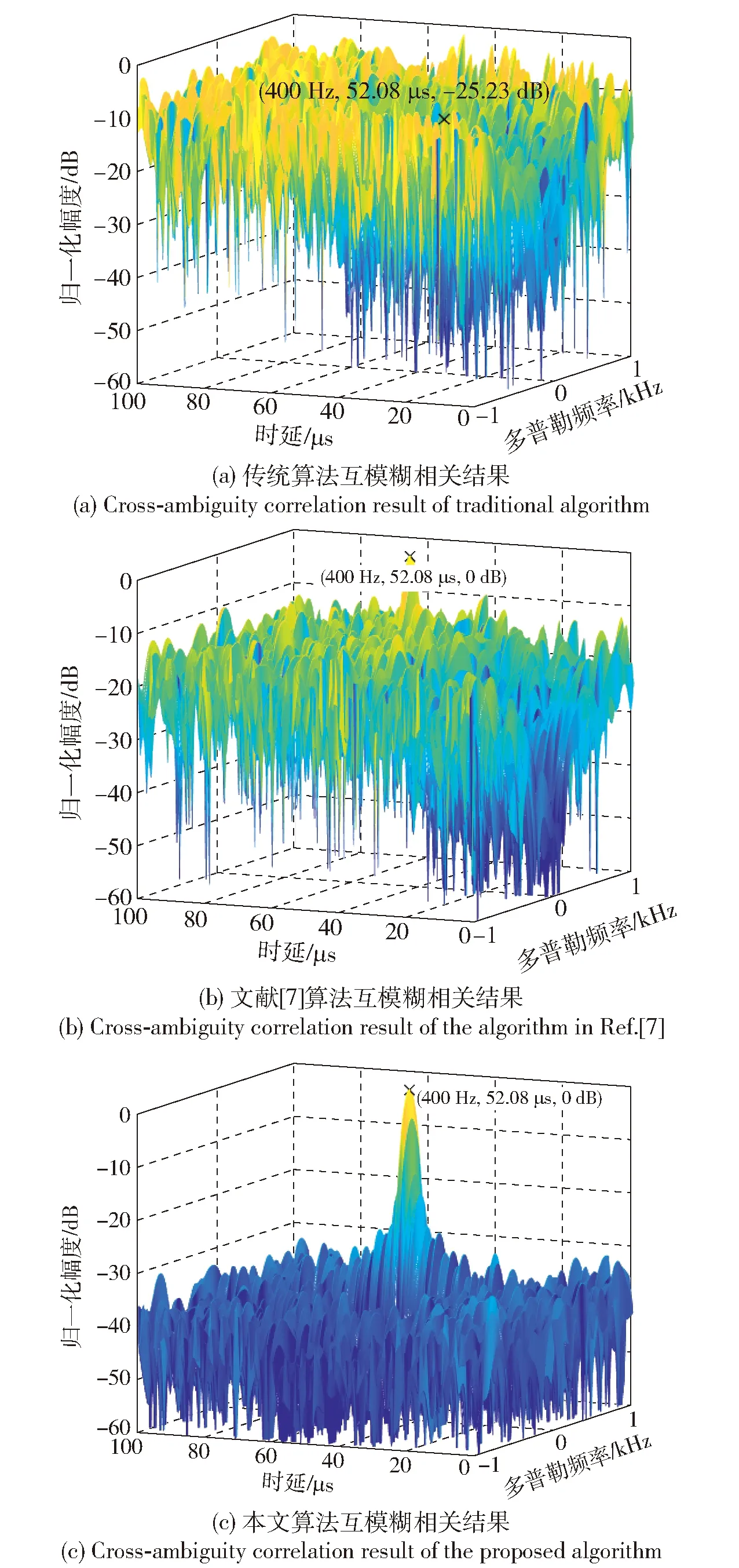
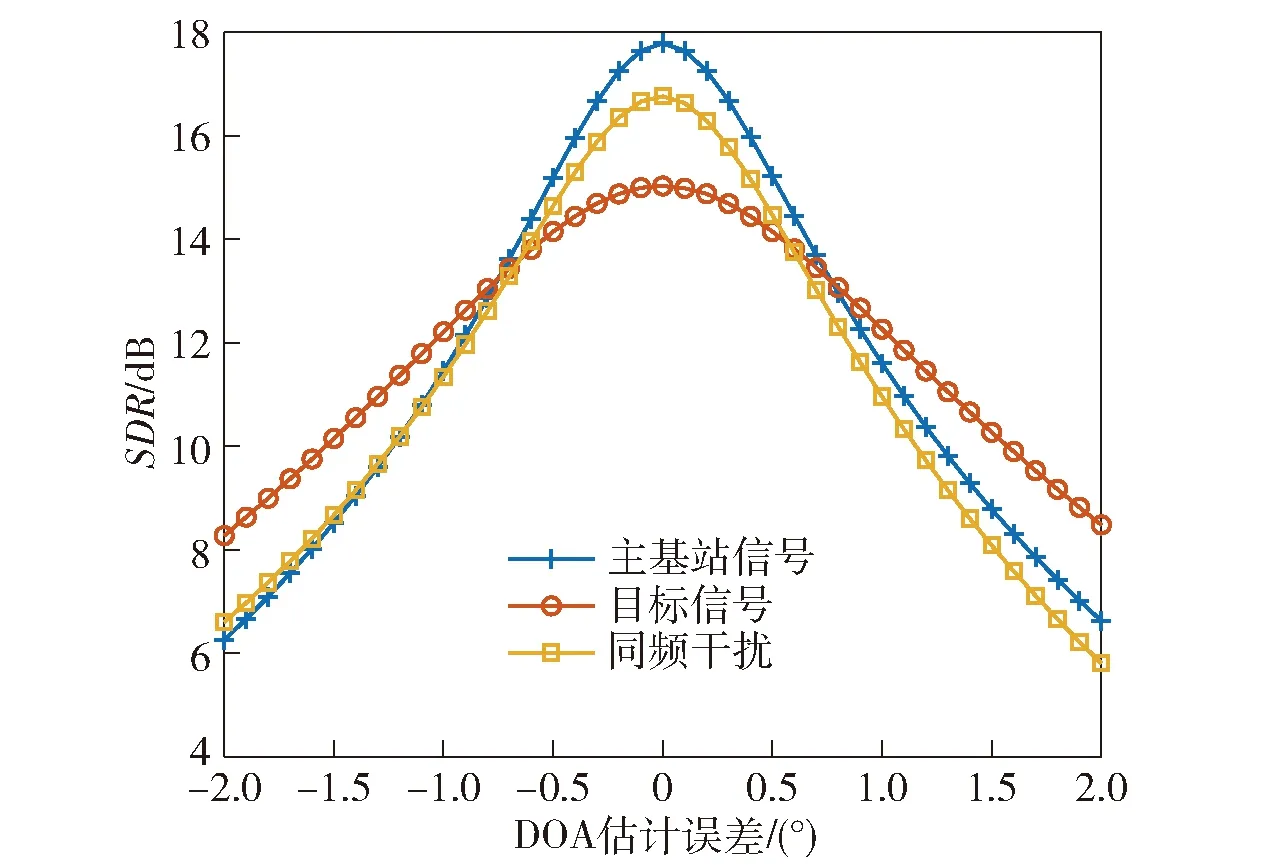
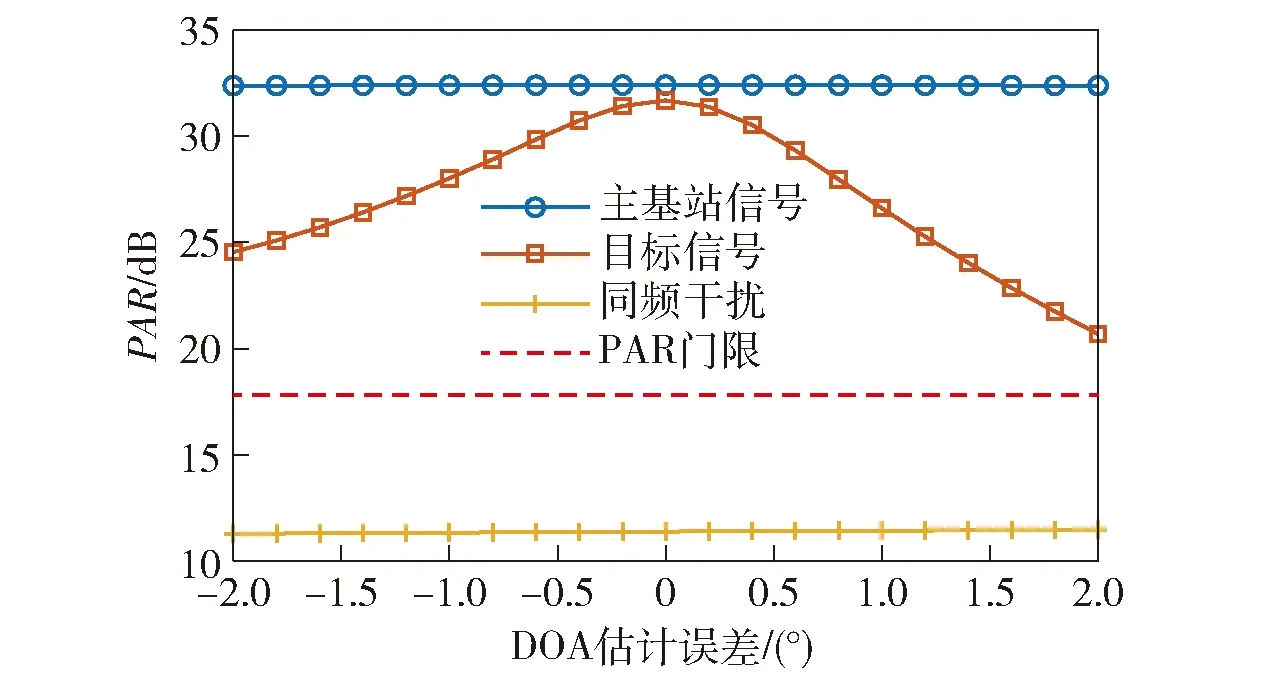
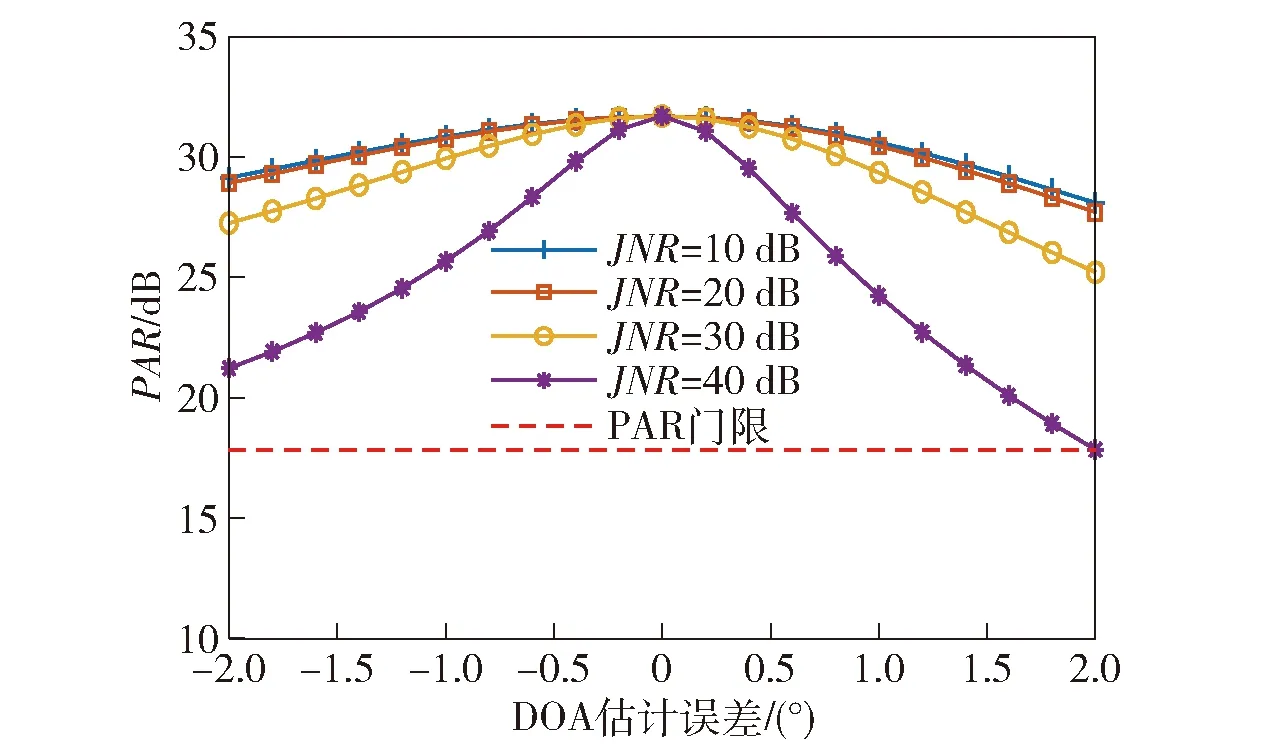
Xl为第l个快拍的阵列接收数据。根据(8)式、(9)式,通过在空间谱上搜索峰值即可得到信号的DOA.设估计得到的N(N (10) 式中:P为使混合矩阵A和中列排序相对应的置换矩阵,P∈M×M. (10)式代入(3)式,利用最小二乘法即可得到源信号S的含噪估计值.值得注意的是,置换矩阵P往往是未知的,在不考虑P的情况下,虽然估计的源信号和源信号S的排序不同,但是并不影响后续的处理。 经过信源分离之后,输出信号主要分为3类:LTE主基站直达波和多径信号、LTE同频基站直达波和多径信号以及目标回波信号。 不同基站发射的LTE信号含有相同的控制信号和同步信号等信息[17],但是经过不同小区ID生成的伪随机码序列加扰后只有较弱的相关性[7],因此LTE基站信号自相关和与同频LTE基站信号互相关输出的差异很明显,如图3所示。 图3 LTE信号自相关及与同频LTE基站信号互相关输出Fig.3 Auto-correlation of LTE signal and cross-correlation output of LTE signal and co-channel LTE base station signal 从图3中可以看出,LTE自相关峰值远远高于LTE信号与其同频干扰的互相关峰值,本文选择采用峰均比(PAR)作为表征二者差异的参数。对于信号s的PAR有 (11) 式中:E(s2)为信号的平均功率;smax为信号s的峰值。 在外辐射源雷达中,利用目标回波信号与参考信号进行互模糊相关,根据互模糊函数中的尖峰位置测量时延差和多普勒频移。互模糊相关函数定义为 (12) 式中:τ为时延差;fd为多普勒频移;T为积分时间;u(t)为参考信号;(·)*表示共轭操作;x(t+τ)为回波信号。 令Ts为信号的采样间隔,令T=PTs,(12)式离散化为 (13) 式中:χ(lτ,lf)为离散化的互模糊相关函数;Lτ、Lf分别为时延和多普勒频率划分的网格数,lτ=0,1,…,Lτ-1,lf=0,1,…,Lf-1. (13)式代入(11)式,互模糊相关结果的PAR可以表示为 (14) 式中:χmax(lτ,lf)为互模糊相关函数最大值。 由于参考信号是提纯后主基站的直达波信号,因此其与主基站信号及其多径信号的互模糊相关结果的PAR值要远大于其与同频基站互模糊相关结果的PAR值。在实际探测环境中,主基站信号、同频干扰信号以及目标回波信号与噪声的比值,即SNR或干噪比(JNR)都是未知的或者时变的,因此PAR参数必须具备在不同SNR或JNR下保持稳定,才能作为区分主基站信号、同频基站信号、目标回波信号的特征依据。通过大量的数值仿真实验,在不同SNR或JNR下,仿真参数见仿真实验,各类型信号互模糊相关的PAR统计均值变化曲线如图4所示。 图4 SNR或JNR变化对不同信号PAR的影响Fig.4 Influence of JNR/SNR changes on the PAR of different signals 由雷达检测理论可知,当虚警率为10-6时,为得到一定的检测概率,信号的SNR通常需要达到10 dB以上。由图4可知,在SNR或JNR为10 dB以上的时候,目标信号、主基站信号、同频基站信号与参考信号互模糊相关结果的PAR统计均值基本稳定,且同频基站信号与另外两种信号有明显区别(PAR差值超过20 dB),这是PAR可以作为信号特征的前提。 从(14)式可以看出信号的PAR值受积分时间影响,由于各类源信号积分时间相同,PAR差值基本不变,仍可以利用PAR的差异进行识别,但是对于PAR门限THPAR的选择带来了困难。 为了避免这种影响,采用从实际接收数据中估计PAR门限的思路,以确保PAR门限能够适用于实际参数和场景。具体操作如下:将接收的实际数据直接与参考信号进行互模糊相关,然后计算相关结果的PAR值,由于目标回波信号中存在同频干扰、目标回波、主基站信号,因此其PAR大于同频干扰的PAR值,同时又小于目标信号、主基站信号的PAR值。在实际场景中,由于主基站直达波功率占主导地位,因此估计出的PAR往往接近只有主基站信号情况下的PAR值。如果直接选取该值,虽然可能有效地识别同频干扰,但是可能会造成算法对于DOA估计失配的鲁棒性不足。因此本文建议取略低于该值10~15 dB的PAR值作为判决门限。在不同数据长度下,不同类型信号的PAR变化曲线如图5所示。从图5中可以看出,PAR判决门限随着数据长度的变化始终能够有效地判别两类信号。 图5 PAR随数据长度的变化Fig.5 Change of PAR with data length 目标回波信号是在LTE主基站信号的基础上经过时延和多普勒调制得到的,因此目标回波信号和LTE主基站信号(包含直达波和多径信号)可以通过搜索互模糊相关峰,判断该峰值的多普勒频率是否大于多普勒阈值THfd来识别是否为目标信号。目标判别流程如图6所示。 图6 目标判别流程图Fig.6 Flow chart of target discrimination 表1 信号参数设置Tab.1 Parameter setting for signals 分别使用传统的外辐射源处理算法(无同频干扰抑制流程)、文献[7]算法和本文算法进行仿真,对比其性能。传统的外辐射源处理算法和文献[7]算法均采用扩展相消杂波(ECA)对消算法[18]。 本文算法需要对分离的N个源信号进行互模糊相关计算,相对于其他算法,互模糊相关的计算量提高了N倍,但是该过程可以并行实现,因此所需的时间和一次互模糊相关运算的时间基本相同。为了简化仿真计算,本文选取目标信号所在的区域τ为(0,100 μs)和fd为(-1 kHz,1 kHz)进行互模糊相关运算,结果如图7所示。 图7 不同算法的互模糊相关结果对比Fig.7 Comparison of cross-ambiguity correlation results of different algorithms 从图7(a)可以看出,由于同频干扰的存在,仅仅采用参考通道的主基站信号进行杂波对消的传统算法无法抑制同频干扰,虽然同频干扰和参考信号的相关性较弱,但是由于同频干扰的幅度远远大于目标回波信号,抬高了整个互模糊相关输出的底噪,导致目标回波信号的互相关峰被淹没在底噪之中,无法识别。从图7(b)中可以看出:文献[7]算法采用盲源分离和级联对消处理流程,一定程度上抑制了同频干扰,但是其效果受选取的杂波抑制算法和设置的参数影响,抑制效果有限,同时盲源分离算法的性能也会影响杂波对消结果;本文算法在信源分离之后,利用LTE同频干扰信号、主基站信号、目标信号三者在距离- 多普勒域上的差异,在理想情况下能够获得不含干扰的目标互模糊相关结果。对比图7(b)、图7(c),本文算法相比文献[7]算法的互模糊相关结果底噪更低,对于弱目标的检测能力更强。 当入射信号SNR较低的时候,m-Capon算法DOA估计误差会增加,为了研究DOA估计误差对源信号分离效果的影响,采用信号失真比(SDR)来表征分离信号和原信号的差异。 源信号si及其分离信号i的SDR为 为尽可能减少随机误差的影响,进行100次蒙特卡洛实验,便于对比,本文将所有接收主基站及多径信号、同频基站及多径信号和目标信号的功率统一设为0 dBW,其他参数和表1相同。根据m-Capon算法在不同SNR下的DOA估计精度[10],本文设置DOA估计误差范围为[-2°,2°],仿真结果如图8所示。 图8 DOA角度估计误差对SDR的影响Fig.8 Effect of DOA angle estimation error on SDR 从图8中可以看出,随着DOA估计误差逐渐增大,估计信源的SDR逐渐降低,这意味着单一源信号中混入了其他源信号成分。对于目标信号而言,目标DOA估计误差过大会导致互相关峰值的降低,甚至可能被底噪淹没。对于同频干扰信号而言,DOA失配过大会导致混入主基站信号或目标信号,导致互模糊相关结果的PAR增大,对主基站和目标信号而言,同频信号的混入又会降低PAR,使得两类信号互模糊相关结果的PAR之差逐渐减小,对后续判决产生影响。对于主基站信号而言,DOA失配会导致混入的目标信号在多普勒门限之外的频率点上形成互模糊相关峰值,进而影响主基站信号和目标信号的判别。 当DOA估计误差为-2°,分离的主基站信号的互模糊相关图如图9所示。在图9(a)中,出现了主基站多径信号对应的互模糊相关峰,在一定程度上降低了PAR,位于66.67 μs的相关峰是由于LTE信号存在周期为66.67 μs的循环前缀引起的,此类副峰的抑制与本文主题无关,不作讨论;分离的同频基站信号的互模糊相关图如图9(b)所示,其互模糊相关图上未出现主基站信号和目标回波信号的相关峰,其PAR值不会有明显变化,这是因为混入的主基站信号和目标回波信号分量太小,形成的相关峰被底噪淹没;分离的目标信号的互模糊相关图如图9(c)所示,由于混入主基站信号,互模糊相关结果出现了主基站信号对应的相关峰,通过多普勒频率的差异,可以明显区分。虽然在图中尚未体现,但是同频基站干扰混入目标信号中的情况也需要注意,当同频基站干扰的功率远大于目标信号时,混入的部分同频基站干扰会使目标信号互模糊相关结果的底噪抬升,导致PAR下降,影响目标的识别。 为了研究DOA估计误差对各类型信号互模糊相关结果的PAR影响,设置DOA估计误差为[-2°,2°],其他参数和表1相同,PAR门限根据实际接收数据估计得到,仿真结果如图10所示。 图10 DOA估计误差对信号互模糊相关输出PAR的影响Fig.10 Effect of DOA estimation error on PAR 从图10可以看出,在所设置的仿真条件下,主基站和同频基站的功率较大,由于DOA微小失配混入的其他源信号没有造成其PAR的明显变化。DOA失配导致目标回波信号的互模糊相关结果PAR下降,通过预设的阈值可以给出正确的判别结果,但是可以发现目标PAR最小值非常接近阈值,极易造成误判。在DOA估计失配的情况下,分离的信号是各源信号的线性组合,因此分离的信号互模糊相关结果的PAR还受到源信号功率差异的影响。对于目标信号而言,DOA失配导致主基站和同频基站信号的混入,其中同频基站信号的混入导致目标信号互模糊相关结果的PAR下降,如果同频干扰基站的功率过大,则有可能造成目标信号的PAR小于预设阈值,造成漏警。 为了研究不同功率的同频干扰基站信号对目标信号互模糊相关结果PAR的影响,设同频基站及多径干扰信号JNR=[10 dB,40 dB],并以10 dB的间隔步进,其他参数和表1相同,仿真结果如图11所示。 图11 目标信号PAR随同频干扰JNR的变化Fig.11 PAR of target signal versus JNR of co-channel interference 从图11中可以看出,随着同频干扰基站的JNR不断变大,在相同DOA估计误差下,目标PAR值不断减小。在JNR=40 dB,信号PAR接近判决门限,可能会造成误判。但是值得注意的是,DOA估计精度不是固定的,随着同频干扰基站的JNR提高,其DOA估计精度也越高,这又减少了其对目标信号的影响。综上所述,本文算法在一定的同频干扰功率范围内仍适用。 在传统基于级联对消思想的LTE同频干扰抑制算法中,多级对消过程会影响整个系统的实时性,并且同频干扰抑制效果容易受到所选取的杂波对消算法以及设定的参数的影响。本文提出了一种基于信源分离和LTE信号在距离- 多普勒域上的差异进行间接同频干扰抑制算法,通过DOA估计得到阵列流型矩阵,实现干扰和目标信源分离。同时结合信号特征,对分离的信号互模糊相关结果进行判别,识别目标信号。相比之下,本文算法具备更优的干扰抑制效果,避免了杂波对消过程,虽然需要进行多次互模糊相关处理,但是可以采用并行处理的方式,减少了多次互模糊相关运算带来的额外时间开销。2.2 基于LTE信号特征的判决策略

3 仿真实验与分析
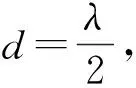
3.1 同频干扰抑制性能分析
3.2 DOA估计误差影响分析
3.3 同频干扰功率影响分析
4 结论

