多阶段平台动态防御的Markov演化博弈模型及迁移策略
王刚, 王志屹, 张恩宁, 马润年, 陈彤睿,2
(1.空军工程大学 信息与导航学院, 陕西 西安 710077; 2.94195部队, 甘肃 定西 730500)
0 引言
平台动态防御是通过转移网络平台的攻击面,提升网络安全性能的一种动态目标防御方法。与传统防御方法相比,平台动态防御在解决攻防信息不对称、安全漏洞多样隐蔽等问题方面具有明显优势,可为目标系统提供规避攻击的机动条件,变被动防护为主动防御。多平台迁移是平台动态防御技术重要的实施手段之一[1],通过对不同主机部署不同的操作系统平台,并由调度中心对上线平台进行周期性地迁移,从而使系统的漏洞信息呈现出动态变化的趋势,平台的迁移规则很大程度上决定了防御的效果,高效的迁移策略是部署多平台迁移的重点和难点。在动态防御过程中,平台迁移应具有随机性,节点在遭受攻击后可按照某种规则选择健康平台上线,并将染毒平台下线清洗。对整个网络而言,节点在遭受多轮次攻击后可能被病毒感染,也会以一定概率将病毒扩散感染到相邻节点,存在“感染—演化—感染相邻节点—相邻节点再演化…”的趋势,攻防过程呈现出多阶段博弈特征,节点平台迁移状态和病毒传播趋势也具有随机性,属于典型有限理性行为,攻防双方结合己方认知调整策略以适应对手的变化,最终达到动态稳定。
对平台动态防御而言,需要把握网络攻防双方的有限理性特征和多阶段博弈特点,通过建模分析多阶段演化博弈机理,并设计针对性迁移策略。
动态目标防御是网络安全领域的新事物,多阶段平台动态防御研究较少,可借鉴成果主要在博弈建模、防御策略制定和效能分析等方面。在防御策略方面:文献[2]针对多目标网络攻防,提出了“游击战”策略;文献[3]以拟态网络技术为基础,设计了针对L2/L3地址的协同动态化伪装策略;文献[4]针对拒绝服务攻击,提出了端口跳变策略,通过添加冗余的端口迷惑攻击者,减少了防御者的损失。在病毒传播和免疫及其效能分析方面:文献[5]针对潜伏型新型病毒特点,提出SEIQRS病毒扩散模型,分析了“去二存一”型病毒的扩散机理和扩散免疫性能;文献[6]设计了非异构边随机中断、非异构边随机重连和单操作系统节点随机跳变3种网络安全优化策略;文献[7]给出了潜伏机制下病毒传播和免疫模型以及网络的稳定性分析,提出利用基本再生数优化网络状态的方法。这些研究主要是从单纯防御视角思考网络安全防御问题,开展策略设计和效能分析,对攻防过程中双方的交互考虑不足。
客观上,网络攻防对抗中呈现出的目标对立性、关系非合作性和策略依存性与博弈论相契合[8],博弈理论和方法是网络攻防科学研究的有效手段。文献[9-11]将贝叶斯法则引入到攻防博弈模型中,利用贝叶斯法则和博弈理论提升防御策略的预测性;文献[12] 利用Stackelberg博弈理论,将用户作为博弈的第三方,同时考虑了防御收益和服务效果,对策略的选择进行了综合评估;文献[13]基于网络杀伤链,建立了基于FlipIt博弈的MTD攻防时机决策模型。这些基于博弈理论的研究主要针对单阶段、单节点的防御,是多阶段平台动态防御的基础。但是,网络攻防过程实质上是攻防双方的多阶段博弈,防御的决策和具体行动应基于对整体网络攻防复杂行为的持续动态分析,由于多数情况下博弈参与者只能获取有限的信息,做出的决策往往是非完全理性的。基于这种认知,文献[14]提出了网络防御的Markov演化博弈模型和防御策略,利用Markov过程的无后效性分析了网络攻防的多阶段、多状态性能;但是所采用的技术主体上还是限制端口数据包、创建地址黑名单和重启数据服务器等静态防御技术,对比多阶段平台动态防御,在基础技术实现环节上存在本质差异。
基于以上分析可知,平台动态防御所面临的攻防环境和过程相对复杂,攻防双方互为博弈,需要借助科学理论和方法,系统考虑攻防博弈的阶段性、收益指标量化和节点连接关系等关键因素:1)网络中各节点之间关系复杂,单阶段博弈模型往往难以完整地描述,可利用Markov过程的无后效性简化节点之间关系,开展多阶段演化博弈研究;2)平台动态防御系统对自身攻击面与资源价值的评估体系是演化博弈的基础,应建立起与多阶段动态博弈相一致的指标体系,在此基础上分析各状态的演化稳定策略;3)网络拓扑结构是网络攻击路径选择的基础,防御策略制定需要考虑网络节点的连接关系,利用网络攻击图,选择出适合网络整体的防御路径。
1 多阶段平台动态防御原理和关键参数
1.1 问题阐述和建模
网络是由多个节点按照一定的拓扑结构和逻辑关系连接而成的,攻击者通常根据网络结构特点制定攻击图,开展针对性的节点感染和网络破坏。在平台动态防御中,平台指承载业务功能的软件和硬件,平台动态防御系统通常由可信控制器、候选平台池和调度程序等组成,节点应用动态防御技术和主动迁移预防网络攻击,一次平台迁移的过程如图1所示。其中,防御方利用虚拟化技术在每个节点上虚拟出多个服务器平台,经由多态化处理,构成在线虚拟服务器平台池。在可信控制器的集中控制下,受攻击节点从虚拟服务器平台池中选择迁移平台,正在运行的平台会在处理完现有的服务请求后进入离线状态,所选择的平台进入上线状态,从而实现平台的迁移。进入离线状态的平台,会把内存和文件系统恢复到初始状态,完成一次清洗。至此,第1个被感染的节点完成了一个防御周期。由于网络环境中始终存在病毒,其他相邻节点存在被感染的威胁,一旦相邻节点被感染,则进入下一阶段的演化。

图1 平台迁移过程Fig.1 Platform migration process
在现实网络环境中,攻击和防御行动不是简单的单回合对决,通常是针对网络整体和多类型节点的多阶段攻防。对于具体的节点而言,迁移的备选平台与当前在线平台的结构相似性直接影响着迁移的成本和迁移完成后对攻击者新一轮攻击的免疫能力,多阶段平台动态防御需要从安全和成本两个方面进行考虑,针对病毒的分布概率和感染性,尽可能减少无效迁移,实现平台动态防御系统在外部病毒环境下对节点状态迁移的提前预测和最优控制。
网络攻防对抗具有周期性和阶段性特征。被攻击节点对于攻击者信息的掌握通常相对有限,很难直接做出最合理的迁移决策,网络节点是由多个服务器组成的,平台的迁移以服务器为单位实施,服务器在攻防周期中根据收益情况自我调整迁移策略,最终整个节点趋向于选择某个稳定策略,被攻击节点趋向稳定的过程是单阶段演化博弈过程。在被攻击节点达到动态稳定后,病毒以一定的概率向周边节点扩散,在新感染的节点上继续进行单阶段演化博弈,最终也达到了稳定状态,周边节点从被感染到动态稳定的过程是多阶段演化博弈过程。参照文献[9],多阶段博弈原理如图2所示。图2中:S0为节点初始安全状态集合,S0={S0,1,…,S0,k,…,S0,T};S为节点被攻击后达到演化稳定状态的集合,S={S1,…,Sk,…,ST};η为状态转移概率。

图2 多阶段演化博弈Fig.2 Multi-stage evolutionary game
整体上看,多阶段平台动态防御是“演化—稳定—演化”的动态博弈过程,并非限定于某一固定状态。
综上所述,在多阶段平台动态防御的Markov演化博弈中:1)单阶段的演化稳定策略是多阶段的基础,多阶段平台动态防御是由多个单阶段的防御构成的,直接对多阶段演化稳定策略进行分析比较困难;2)转移概率η决定了多阶段演化的趋势,转移概率的值与攻防双方的状态和网络结构有着密切关系,确定起来相对复杂,η的合理设置,是演化博弈的关键。因此,对多阶段平台动态防御的分析可以从单阶段防御和确定的转移概率入手。
1.2 关键参数与收益计算
定义1资源重要程度Cr,指在一次完整的攻防过程中,攻击方目标资源的重要程度,由节点的度决定。
定义2攻击面转移成本Cs,指平台迁移时需要付出的系统开销。
攻击面转移成本与平台差异程度有关,平台越相似,成本越低。
定义3负面影响成本Cn,指平台迁移时,带来的服务质量下降。
定义4攻击成本Ca,攻击者进行攻击时所付出的代价。
攻击成本与漏洞的威胁级别有关,漏洞的级别越高,攻击成本就越低。
定义5感染概率λ,指平台被病毒感染的概率。若操作系统和病毒类型不同,λ=0;若相同,则λ为漏洞利用成功概率。
综上,防御者的收益Ud可表示为
Ud=(1-λ)Cr-Cs-Cn.
(1)
攻击者收益源于感染平台后得到的收益,与感染概率有关,则攻击收益Ua可表示为
Ua=λCr-Ca.
(2)
2 多阶段平台动态防御的Markov演化博弈模型
2.1 单阶段平台动态迁移演化博弈模型
单阶段演化博弈模型主要针对单一网络节点的平台动态迁移,对网络的整体分析建立在节点分析基础上。
定义6单阶段Markov平台动态防御演化博弈模型(SPDDE),表示为4元组SPDDE=(N,B,P,U),其中:
1)N=(Nd,Na)为演化博弈的参与者空间。其中,Nd为防御方,Na为攻击方。
2)B=(Sd,Sa)为双方策略空间,其中:攻击方策略表示为Sa={Sa, i|1≤i≤m},m为攻击者策略总数;防御方策略表示为Sd={Sd, j|1≤j≤n},n为防御方迁移策略总数。
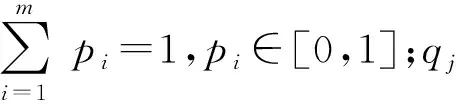
4)U={Ud,Ua}是博弈收益集合。
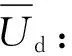
(3)
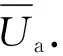
(4)
2.2 多阶段Markov平台动态迁移演化博弈模型
定义7多阶段Markov平台动态防御演化博弈模型(MMPDDE),可表示为9元组MMPDDE=(N,T,B′,P,ξ,S0,S,η,U),其中:
1)N=(Nd,Na)是参与者空间。
2)T是多阶段博弈的阶段总数,k是博弈当前所处阶段,k∈{1,2,…,T},T∈N+.
3)B′=(S′d,S′a)是双方策略空间,其中:防御方策略为S′d={Sd,k,j|1≤k≤T,1≤j≤n},Sd,k,j表示第k阶段的可选策略;攻击方策略S′a={Sa,k,i|1≤k≤T,1≤i≤m},Sa,k,i表示第k阶段的可选策略。

5)ξ为折现因子,用于表示当前收益与初始收益的折现情况,满足0≤ξ≤1.
6)S0={S0,1,…,S0,k,…,S0,T}是节点初始安全状态集合。
7)S={S1,…,Sk,…,ST}是节点被攻击后达到演化稳定状态的集合。
8)η表示状态转移概率,ηij=η(Sj|Si)表示系统由状态Si转移至状态Sj的概率。本文设状态转移概率为固定值。
9)U={Ud,k,Ua,k}是博弈收益集合,Ud,k和Ua,k分别表示防御者和攻击者在第k阶段的收益。
用目标函数F表示当前收益与折现收益之和,并作为选择策略的标准[15]。考虑系统在不同阶段时,双方收益也不同,用折现因子ξ体现未来收益值和当前收益值的区别。分别用Fd,k(S0,k,Sk)和Fa,k(S0,k,Sk)表示防御方和攻击方在k阶段的目标函数,具体表述为
(5)
3 博弈均衡求解
3.1 博弈均衡分析
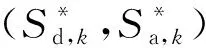
(6)
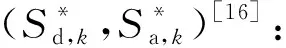
(7)
定理1多阶段Markov平台动态防御演化博弈存在混合策略下的纳什均衡。
证明在多阶段Markov平台动态防御演化博弈中,存在多个单阶段演化博弈过程,这些过程相互独立并且相似,待选策略的空间也是有限的,因此存在混合策略下的纳什均衡[14]。同时,根据定义的转移概率和收益计算方法可知,存在与MMPDDE对应的有限随机博弈,且收益函数为凸函数。根据有限随机博弈的均衡策略存在性定理[17-18],该有限随机博弈存在混合策略下的纳什均衡,通过该纳什均衡可得MMPDDE对应的混合策略纳什均衡。综上,定理得证。
3.2 均衡求解
3.2.1 单阶段演化博弈均衡求解
由(1)式计算防御方的期望收益和平均收益:
(8)
由(2)式得到防御方的复制动态方程:
(9)
对于攻击方,同理可得
(10)
(11)
3.2.2 多阶段演化博弈均衡求解
采用动态规划法求解多阶段均衡策略:
(12)
3.3 最优迁移策略选取算法设计
根据博弈均衡求解,设计如下最优迁移策略选取算法。
算法:MMPDDE模型的最优迁移策略选取算法
输入:MMPDDE模型
输出:最优迁移策略
BEGIN
1.Initialize;
2.构建攻防策略空间与状态集合;
3.初始化状态转移概率ηi,j=η(Sj|Si);
4.For(k=1;k≤T;k++)
{

6.计算在攻防策略对(Sd,k,j,Sa,k,i)下的双方收益ak,i,j、bk,i,j;
8.求解各个阶段的演化博弈均衡策略(Sd,k,Sa,k)
};

10.根据3.2节的动态规划法,以maxFd,k(S0,k,Sk)和maxFa,k(S0,k,Sk)为目标函数,求解方程组(12)式,得到均衡解;
END.
算法的时间复杂度为O(k(m+n)2)。将所提模型与已有模型对比,结果如表1所示。

表1 本文模型与已有模型对比分析Tab.1 Comparison of the proposed model and themodels in Refs.[13,14,15]
已有模型主要利用静态防御,如打补丁、关闭服务器、删除可疑账户等手段,基于博弈参与者双方的非完全理性特征,利用演化博弈开展单阶段或多阶段的研究。鉴于静态防御理念和技术的局限性[1],动态目标防御等新型主动防御成为解决高水平持续性威胁等网络安全问题的重要手段,通过多阶段演化博弈确定平台迁移规则,对平台动态防御的实际部署和网络安全防御系统运行维护具有重要价值。
4 仿真实验与分析
4.1 网络环境描述
按照迁移平台的多样性、动态性特点,通过虚拟机在网络节点上构建冗余平台,部署平台动态防御环境。利用Nessus工具扫描实验网络环境,根据国家信息安全漏洞库[19]和美国国家漏洞库[20]有关数据,参考文献[21]中漏洞利用成功概率计算方法,获得平台漏洞信息(见表2),平台漏洞利用成功率即为病毒感染概率。根据系统漏洞和网络拓扑结构,得到如图3的攻击图。设计状态集合为S={S1(攻击入侵检测系统),S2(攻击Web服务器),S3(攻击堡垒主机),S4(控制数据库账户或窃取信息),S5(在文件服务器上植入后门),S6(获取内网用户敏感信息)}。

表2 漏洞信息Tab.2 Vulnerability information

图3 网络攻击图Fig.3 Network attack graph
设初始上线平台类型为平台1、平台2和平台3:对应各阶段可用防御策略集S′d={Sd,k,1(平台1→平台2),Sd,k,2(平台1→平台3),Sd,k,3(不迁移)};对应各阶段可用攻击策略集S′a={Sa,k,1(利用类Windows系统漏洞),Sa,k,2(利用类Linux系统漏洞),Sa,k,3(不攻击)}。
4.2 数值计算
参照历史数据和专家经验确定转移概率的方法[14,22],设状态转移概率为固定值,转移概率如表3所示。为了便于比较,设节点初始状态均为类Windows操作系统平台。

表3 跳变概率Tab.3 Hopping probability


表4 双方收益Tab.4 Two sides benefits
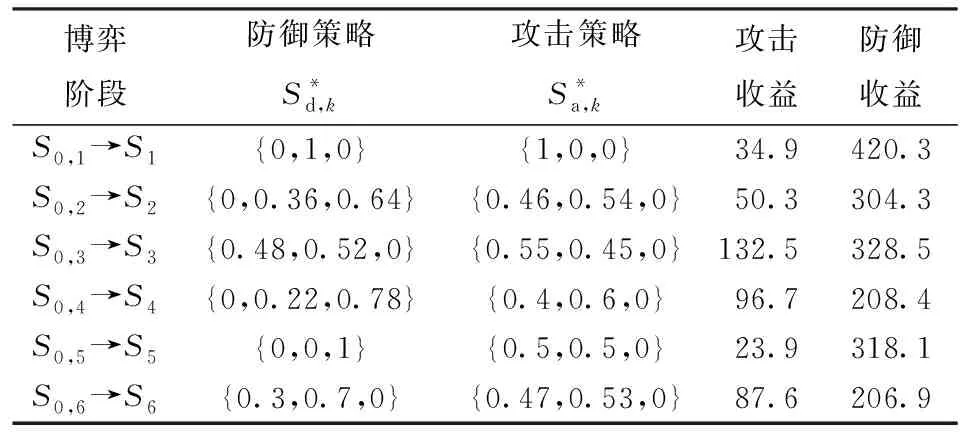
表5 均衡策略收益Tab.5 Equilibrium strategy benefits
4.3 结果分析
设攻击者以数据库服务器S0,4为目标发动攻击,则有可选路径1:S0,1→S1→S0,3→S3→S0,4→S4和路径2:S0,1→S1→S0,2→S2→S0,4→S4.路径1是先获取堡垒主机权限后,通过堡垒主机获取Web服务器的权限,再获取数据服务器权限;路径2通过获取Web服务器权限后,再获取数据服务器权限。路径1的攻击者收益Ua,p,1=264.1,防御者收益Ud,p,1=957.2;路径2的攻击者收益Ua,p,2=181.9,防御者收益Ud,p,2=933.由Ud,p,2-Ua,p,2>Ud,p,1-Ua,p,1可知,对防御者来说,路径2的净收益更高。这是由于堡垒主机的重要程度通常比较高,一旦堡垒主机被攻陷,整个防御网络都将处于被动的局面。因此,防御者可考虑从平台的动态迁移入手,提高堡垒主机的防御强度。
5 结论
本文针对平台动态目标防御开展多阶段演化博弈研究,分析多阶段平台动态防御的技术原理,构建相应的Markov演化博弈模型,设计攻防双方收益的量化方法,求解多阶段演化均衡策略,通过仿真验证了所提演化博弈模型和迁移策略的有效性。后期研究中,可以在建模和策略研究中进一步考虑时间因素,增加收益计算的准确性,提升模型和策略的可用性。

