时间尺度上约束Hamilton系统的Noether对称性和守恒量

郑 明 亮

(无锡太湖学院 机电学院, 江苏 无锡 214064)

现代数学和物理力学的一个交叉部分是动力学系统的对称性与守恒量. 当力学系统Lagrange函数的Hess矩阵不满秩时称为奇异系统, 它在相空间中用Hamilton形式表述, 被称为约束Hamilton系统[1]. 在数学物理和工程技术等领域, 许多重要的动力学问题均符合约束Hamilton系统模型, 如电磁场、 光的横移现象、 量子电动力学行为和超弦理论等. 约束Hamilton系统对称性理论和守恒量的相关研究已取得较多成果. Dirac[2]首先提出了约束Hamilton系统的量子化问题； Li等[3]研究了经典水平下奇异系统的Noether对称性与守恒量； Mei等[4]研究了奇异Lagrange系统Lie对称性与守恒量； 张毅等[5]研究了奇异Hamilton系统Lie对称性与守恒量; 罗绍凯[6]研究了奇异Hamilton系统的Mei对称性与守恒量, 并比较了Mei对称性、 Noether对称性和Lie对称性的差异. 但目前奇异系统理论的研究大多以连续时间为基础, 即导数仍然是经典导数的意义, 但在一般动力学系统中, 时间尺度[7-8]的微积分性质更具广泛性, 它可将连续和离散统一, 揭示连续和离散的异同点, 并能更清晰、 更准确地刻画连续与离散系统以及其他复杂动力学系统的物理本质.

目前, 关于时间尺度上动力学系统的对称性与守恒量的研究大多数针对非奇异系统, 文献[9-11]研究了时间尺度上的变分、 Lagrange系统的Noether理论和Hamilton系统动力学对称性； 文献[12-16]研究了时间尺度上约束力学系统的理论框架. 由于奇异系统自身的内在约束, 因此其时间尺度上的变分问题、 对称性和守恒量对分析力学和工程科学具有重要意义. 基于此, 本文在文献[17]的基础上, 对存在约束的力学系统, 采用时间不变的无限小变换, 推导时间尺度上奇异Hamilton系统的Noehter对称性理论, 并举例说明结果的应用.

1 时间尺度上约束Hamilton系统的正则方程

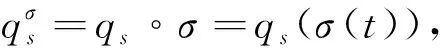
引进时间尺度上广义动量和Hamilton函数为

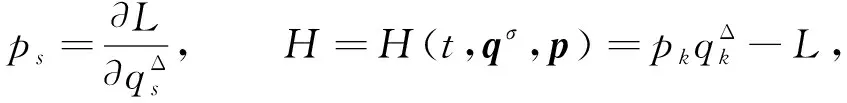
(1)

时间尺度上非保守Hamilton量为

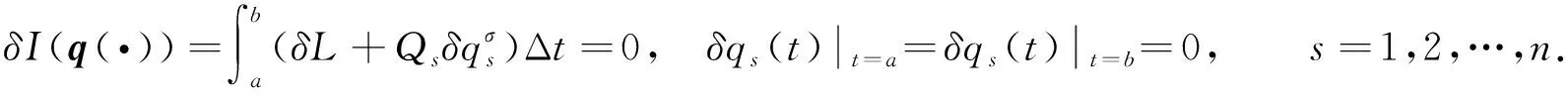
(2)

将式(1)代入式(2)并进行变分运算可得

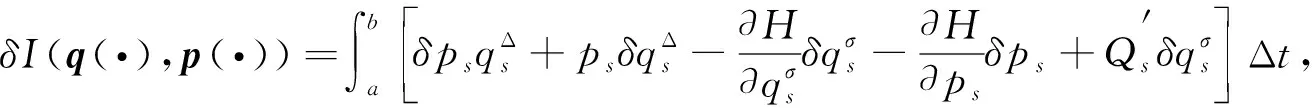
(3)

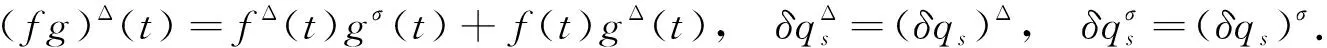
(4)

利用边界条件, 式(3)可化简为

φj(t,qσ,p)=0,j=1,2,…,r.

(6)

这些约束应满足虚位移和等时变分的限制条件:

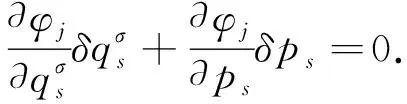
(7)

引入Lagrange乘子λj, 先用λjΔt乘以式(7), 再在区间[a,b]上积分, 可得

(8)

将式(8)与式(5)相减可得

(9)

利用Dubois-Reymond引理[7], 可得系统的正则方程为

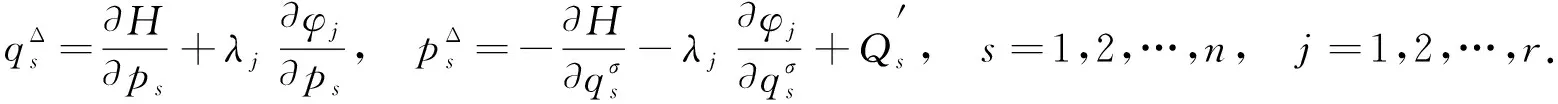
(10)

若式(6)为第二类约束[5], 则可得所有的Lagrange乘子λj=λj(t,qσ,p).

式(10)即为时间尺度上约束Hamilton系统的正则方程, 在形式上与时间连续完整非保守奇异系统是一致相似的, 表明引入时间尺度上的微积分未对正则方程的单一结构产生影响, 仅增加了导数计算难度.

2 系统的Noether对称性

在时间尺度上, 约束Hamilotn系统的正则作用量为

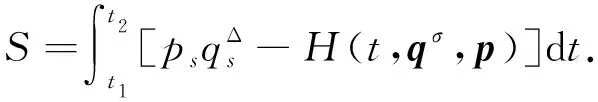
(11)

时间不变无限小变换为

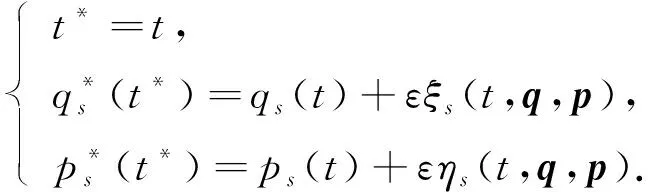
(12)

对于任意的子区间[ta,tb]⊆[a,b], 若式(11)在式(12)的变换下满足

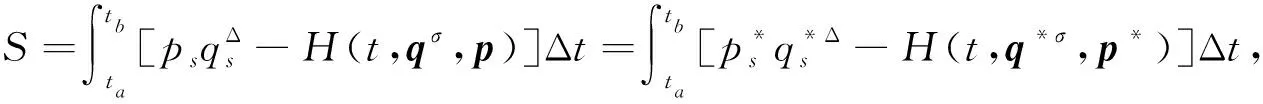
(13)

则称这种不变性为时间尺度上约束Hamilton系统在时间不变的无限小变换下的Noether对称性.

化简方程(13)得

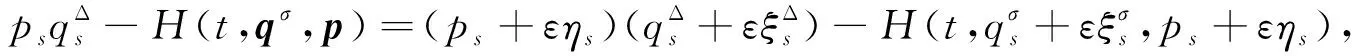
(14)

将式(14)两边对ε求导, 并令ε=0, 可得

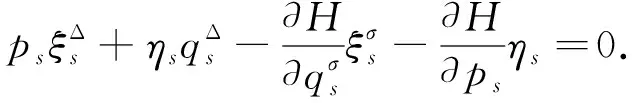
(15)

将正则方程(10)代入式(15)可得

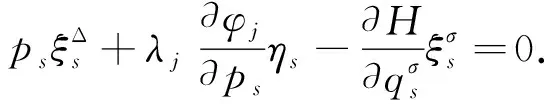
(16)

式(16)即为时间不变变换下时间尺度上约束Hamilton系统的Noether恒等式.

3 系统的Noether类型守恒量

若无限小生成元满足式(16), 且同时存在规范函数G=G(t,qσ,p)满足结构方程

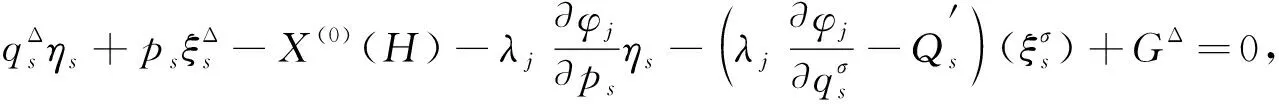
(17)

则时间尺度上约束Hamilton系统的Noether对称性可导致守恒量

IN=psξs+G=常数，

(18)

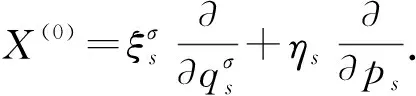
证明： 对式(18)求上三角导数得

(19)

利用式(18), 进一步化简(19)可得

证毕.

4 应用实例

例1设时间尺度、 系统的Lagrange函数和非有势广义力为

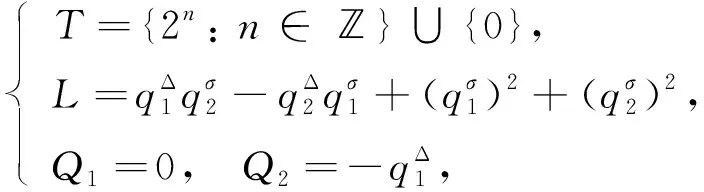
(21)

在相空间中研究系统的Noether对称性和守恒量.

由于系统Lagrange函数的Hess矩阵的秩为0<2, 因此系统奇异. 系统的广义动量为

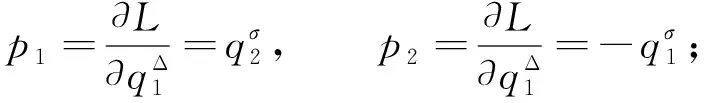
(22)

系统的Hamilton函数为

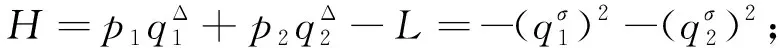
(23)

系统的内在约束方程为

(24)

Lagrange乘子为

(25)

时间尺度上向前跳跃算子和步差算子为

σ(t)=2t,μ(t)=t.

(26)

由式(10)可得系统的正则方程为

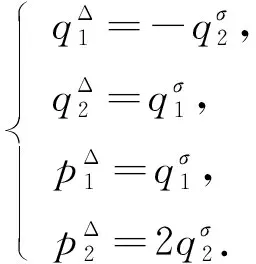
(27)

根据Noether等式(16)可知, 系统无限小生成元ξ0,ξs,ηs满足

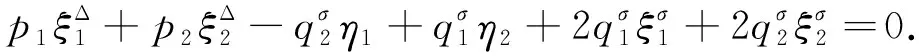
(28)

利用关系式

(29)

可得相应的无限小变换生成元

ξ0=0,ξ1=1,ξ2=1,η1=2,η2=-2.

(30)

将式(30)代入结构方程(17)可得

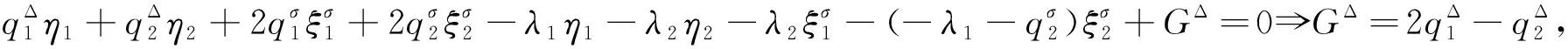
(31)

将式(31)代入系统Noether守恒量式(18)可得

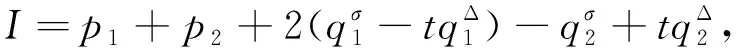
(32)

式(32)即为时间尺度上约束Hamilton系统的Noether类型守恒量.

综上, 本文对时间尺度上非保守约束Hamilton力学系统的Noether定理进行了研究： 通过对内在约束方程的变分处理, 建立了时间尺度上奇异系统的Hamilton原理和Hamilton正则方程； 考虑时间不变的群变换, 给出了时间尺度上约束Hamilton系统的Noether对称性的定义和Noether等式, 其为经典力学Noether对称性的一致延深； 通过构造规范函数, 给出并证明了时间尺度上的Noether类型守恒量, 并通过算例验证了本文方法和结果的有效性. 由于时间尺度的任意性, 因此该方法可进一步应用到时间尺度上非完整约束奇异系统对称性与守恒量的研究中.