面向高速列车监测数据的并行解压缩算法

王周恺，张 炯，马维纲，王怀军

（西安理工大学计算机科学与工程学院，西安 710048）

（*通信作者电子邮箱zkwang@xaut.edu.cn）

0 引言

为保证高速列车安全、有效地运行，需要在列车运行过程中利用各种传感器，通过铁路综合数字移动通信系统（Global System for Mobile Communications-Railway，GSM-R），对列车的运行时各部件的状态进行监测［1］。遵照4 级中国列车控制系统（Chinese Train Control System-4，CTCS-4）的设计要求，各类车载传感器在列车运行时，收集列车车厢及关键部件的实时数据状况，包括速度、功率、风力、湿度等；再采用变长编码技术（Variable Length Coding，VLC）对收集的数据进行压缩，最后将压缩数据通过GSM-R 传输并存储于控制中心；相应地，工作人员如果需要分析列车状态，则先对数据进行解压缩，在此基础上，再对解压缩结果进行分析，从而发现列车运行中可能产生的故障问题，并及时修复故障，避免潜在风险的发生［2］。

然而，由于采用了变长编码技术压缩数据，针对高速列车监测数据的分析效率通常较低，这是因为采用变长编码技术的数据压缩方法通常先将数据进行等长划分，再将划分结果按照频次排序并利用哈夫曼树进行编码，从而获得更高的压缩比［3］；但这种利用变长编码技术压缩的数据由大小不同的数据块组成，且块间边界难以确定。所以目前针对此类数据的解压缩方法通常是从数据的起始位置开始，按照各数据块的组成顺序，从头到尾依次对数据进行逐块解压缩［4］。而这样的串行解压缩过程亦无法被并行化，因为在当前数据块未解压缩之前，其后续数据块的起始位置无法得知，因此，当前针对高速列车监测数据的分析过程受变长编码解压缩算法的影响，效率较低［5］，难以满足在春运等高负荷环境下对海量监测数据及时处理的需求［6］。

为解决传统串行解压缩算法无法高效处理高速监测数据的解压缩问题，基于针对变长编码压缩数据的结构研究，本文以多核领域常用的推测并行技术作为手段，提出一种面向高速列车监测数据的并行解压缩算法。该方法使用推测手段消解压缩数据的组成顺序对解压缩算法执行流程的影响，使压缩数据的处理过程得以并行化；然后在通用大数据分析引擎Apache Spark 上实现并行流程，借助分布式计算框架提供的强大算力，极大地缩短数据解压缩需要的时间，为高速列车监测数据的解压缩提供高效可靠的新方法，从而进一步缩短针对高速列车监测数据的分析时间，提高针对高速列车监测数据的处理效率。

1 动机

为保证高速列车的安全、稳定运行，按照CTCS-4 列控系统设计要求，列车在车厢内部和各个关键部件处安装不同类型的传感器，实时监控运行状态［7］：例如，大量温度传感器遍布车厢和车体、监控变压器以及驱动轴、定子转轴、齿轮等关键部位，实时测量其温度；安装在车轴部位速度传感器实时监测列车运行时速和车轴转速；空气制动力、风管压力、连接端车牵引力等由车厢外部的测力传感器收集；而中间电压、牵引变流器功率、电制动功率、区域控制单元电压等信息的记录由各式复杂的电压、电流传感器负责。这些传感器以每秒一次的采集频率记录列车运行时各部件的状态，并通过列车内部的有线传输系统，将采集数据传送给车载安全计算机（或称欧洲安全计算机（European Vital Computer，EVC）），计算机对传感数据进行整理，以日志文件的形式存储于车载机柜的硬盘中。在达到一定数据量后，对日志文件进行压缩，再通过GSM-R网络提供的通信网络将压缩数据传输给列车控制中心（Train Control Center，TCC）；最后，TCC将压缩数据分类整理，存入分布式数据库HDFS（Hadoop Distributed File System）中。当需要对列车监测数据进行分析时，后台工作人员从HDFS中取出数据并进行解压缩，再对解压缩结果进行分析，进而对列车状态进行判断［8］。

高速列车监测数据具有如下特点：数据按时间序列采集；数据类型为双精度浮点型；相邻数据间差距较小；部分数据内容可为空；监测数据种类较多；数据量巨大［9］；此外，收集的监测数据还需要进行传输和保存。综上所述，为保证监测数据的有效存储和安全传输，需要将由监测数据构成的日志文件进行压缩。目前针对监测数据的压缩常采用动态哈夫曼编码（Dynamic Huffman Coding）技术［10］实现，这种压缩数据由一系列不等长的数据块组成，如图1 所示。每个数据块包括块头标号、动态哈夫曼树、压缩内容以及块尾标号。其中：块头标号用以描述当前压缩数据块的特性；动态哈夫曼树是数据压缩和解压缩的依据；压缩内容存储了使用动态哈夫曼树压缩数据后的结果；块尾标号由一串特定字符组成，用以标识压缩数据块的结束。

针对这类数据，传统的解压缩流程从监测数据的起始位置开始，按照数据块的组成顺序，利用动态哈夫曼树，逐块对其中的压缩内容进行还原，通常效率较低。算法1和图2分别展示了变长解压缩算法的伪代码和相应的依赖关系分析图。从算法1 可知，传统算法的每一轮循环解压一个完整的数据块；当一个数据块被解压完后，表示位置信息的pos 更新，指导下一个数据块的解压缩。如图2 所示，该解压缩算法共包含三条依赖：由变量eof引发的控制依赖、由内部循环中的pos引发的数据依赖，以及由out_stream 变量引发的数据依赖。这些依赖关系共同作用，阻碍了多重循环的并行执行。在数据量特别大的情况下，输入数据中包含大量的数据块，因此由pos所引起的数据依赖是影响算法并行执行的最大因素。

为提升针对变长编码压缩数据解压缩效率，目前主流的解决思路是采用软硬件协同的方法，通过加速单个数据块的处理过程，提高针对变长编码压缩数据的整体压缩效率。例如将传统解压缩算法移植到图形处理器上，通过任务分解和统一计算设备架构（Compute Unified Device Architecture，CUDA）提升算法效率［11-12］。此外还有运用大数据计算引擎，设计基于分布式平台的数据解压缩算法［13-14］。但此类方法的思路主要聚焦于并行化哈夫曼树还原压缩内容的过程，并使用大量计算资源对该过程进行加速，通常效果不佳。从对算法运行机制的深层次分析可知，这些优化方法只能缩短单个数据块的处理时间，而数据解压的整体过程仍然是按照压缩数据的组成顺序串行进行的。如图2 所示，若不能消解算法中的数据依赖对执行顺序的影响，从根本上将串行解压缩的过程并行化，则对解压缩算法的性能优化效果有限［15］。

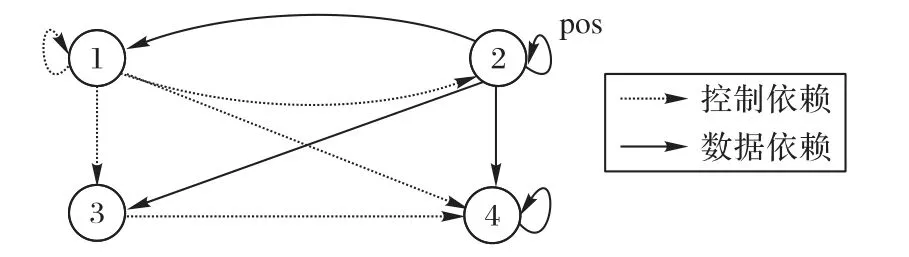
图2 传统变长解压缩算法的伪代码和依赖关系图Fig.2 Pseudo codes and dependence relationship diagram of conventional variable-length decompression algorithm

要从根本上提升数据解压缩算法的并行度，需要在解压缩之前，将压缩数据划分成一系列可以被独立解压缩的数据块的组合，再同时解压缩这些数据块，从而使数据解压缩过程并行化。但由于变长编码技术的影响，数据块间的边界在解压缩前通常难以确定，随意划分可能会造成对压缩数据块完整性的破坏；而数据块内部的任何部分都存在与压缩内容重复的可能性，因此也不具备作为划分数据块边界的功能。

针对上述困难，本文以推测技术为手段，实现高速列车监测数据的并行解压缩。首先，以压缩数据的块尾标号作为划分数据块边界的依据，假定不存在压缩内容与块尾标号重复的情况，对数据进行尝试性划分；然后设计推测校验方法，消除错误划分的影响，再将划分结果进行推测性的并行处理；最终将并行处理结果合并。通过这种方式并行化原本串行的数据解压缩过程，从而提升变长压缩数据的解压缩效率。

2 算法设计

基于上述对存在问题和解决思路的描述，面向高速列车监测数据的并行解压缩算法设计如下：算法被分为推测划分、推测检验、并行解压缩和结果合并四个部分。

2.1 推测划分

作为算法的第一部分，推测划分的目的是在数据解压缩之前，尽可能地将压缩数据划分成独立完整的数据块，使这些数据块可以不依赖于先前数据块所提供的位置信息而被独立处理。为达成该目的，需要确定推测划分的依据和粒度。

首先，推测划分的依据按照如下方法确定。在变长压缩数据内部，数据块由四部分组成，其中动态哈夫曼树和块尾标号的内容固定不变，其他部分会随着压缩内容的不同而变化［15］，因此，首选动态哈夫曼树或块尾标号作为推测划分的依据；又因为块尾标号由动态哈夫曼树编码表中最长的编码构成，其长度通常小于压缩数据块中的动态哈夫曼树，更容易被识别和提取［16］。综上原因，在算法设计中，拟选取块尾标号作为依据，对压缩数据进行推测性地划分。

确定划分依据的基础上，再确定推测划分的粒度。一般来说，针对数据的划分粒度太细密，会使得划分工作变得非常繁琐，影响后期并行解压缩任务的数量，使派生并行解压缩任务的工作量陡增，影响算法的整体性能表现；但如果将数据划分得过大，又会导致划分数据的传输和并行处理成本增加，也会影响到整体的性能［17］。因此，数据的划分粒度是影响到算法效率的重要因素。

为了确定划分粒度，需要建立其与算法运行时间的理论模型。假设在推测并行解压缩算法中，单个并行解压缩任务的执行时间F相等，则算法总耗时T如式（1）所示，总耗时T由并行任务的派生耗时和执行耗时组成，其中λi为单个并行任务派生耗时，M表示任务总量，C表示分布式集群中工作节点数量。

此外，由于数据块划分数量M与压缩数据总大小E、划分粒度H程反比，故M=。如果假设每个并行任务的派生耗时λi近似，则有=M×λ，用该式对式（1）中的M和λ进行替换，可得算法耗时T与划分粒度H及单个并行任务的执行时间F的关系如式（2）所示：

其中：E为压缩数据总大小，λ为单个任务派生耗时，μ为算法执行时间系数，C为节点数，且这几个均为常量。因此式（3）可以表示为划分粒度H与算法耗时T的关系，其函数图像如图3所示。

图3 推测划分粒度与算法耗时函数关系图Fig.3 Relationship between speculative division granularity and algorithm running time

从实际情况出发，划分粒度应满足条件H>0，故选取第一象限进行分析。观察函数图像可知，当划分粒度H趋近于0时，分块数量趋近于+∞，会导致任务分派节点的负载过大，派生任务耗时所占比重不断增加，进而影响算法效率。

为使算法耗时最短，需对式（3）进行求导，并令导数为0，易知当划分粒度H满足式（4）时，使T取得极小值。

综上分析，式（4）即为确定推测划分粒度的数学模型，通过该模型可以确定当H满足条件时，算法执行时间最短。

针对采用变长编码的压缩数据，其数据大小E、集群节点C和任务派生平均时间λ可以在算法执行前得知；而μ的取值依赖于输入数据类型，一般取均值31 250［16］。经过计算，可得H为29 MB。最后，为了使划分粒度数值快速收敛，一般选取大于H且满足2的n次幂的最小值。最终，在推测并行解压缩算法中，将推测划分粒度确定为32 MB。

在确定划分依据和粒度的基础上，算法以输入数据中首个数据块的块尾标号为依据，以32 MB 为最短步长，逐字节地扫描输入数据，以确定推测划分点，如图4 所示，对数据进行初步的推测划分。然而由于该划分策略是以推测技术为基础，因此存在因数据巧合，出现压缩内容与块尾标号相同而被认为误认为是划分点的情况，所以在推测划分结束后，需要对推测划分结果进行检验，以确保划分结果的正确性。

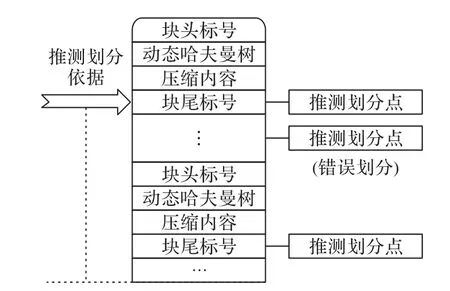
图4 推测划分过程示意图Fig.4 Schematic diagram of speculative division

2.2 推测检验

由于通过推测所获得的数据划分点并不能保证数据块的完整性，因此需要对推测划分结果进行验证。参考其他基于变长编码的并行数据压缩方法［18］，本文算法提出头校验、哈夫曼树重建和数据长度校验三种检验手段，通过这三种检验手段的结合，检测划分结果是否正确。

头校验是指检验划分结果的前3 位是否遵循块头标号的编码规则。一般来说，压缩数据块的前3 位只能是010 或000，分别代表该压缩数据块是遵循动态编码标准的压缩数据块或是未被压缩的非压缩数据块，如果划分结果的前3 位不是010或000，则该划分为错误划分。

结束头校验后，根据头校验的结果，继续对划分结果进行检验，即哈夫曼树重建和数据长度校验。哈夫曼树重建是指当划分数据的前3位为010时，代表当前划分结果可能是以压缩数据块开头的一组数据，此时可以通过利用010 后的数据进行动态哈夫曼树的重建来判断：如果无法重建动态哈夫曼树，则该划分为错误划分。数据长度校验是指当划分数据的前3位为000时，代表当前划分结果可能是以非压缩数据块开头的一组数据，因此需要对非压缩数据块的长度进行判断：在采用变长编码的压缩数据中规定，非压缩数据块的长度不能超过16 KB［19］。因此，如果从000后到下一个块头标号之间的字段长度超过16 KB，则该划分为错误划分，反之则为正确划分。

为详细解释推测检验原理，图5 详细模拟了该过程。在某段高速列车监测数据中，压缩数据的块尾标号为10111111，用块尾标号将压缩数据划分为四组后，对四组数据的推测检验过程如下：首先进行头校验，由图5可知，第3组数据划分的开头011 不符合压缩数据块的标准头格式，因此未能通过头校验，该划分错误。其余三组划分数据根据头校验结果的不同，继续进行后续校验：在对开头为010 的划分结果进行哈夫曼树重建的过程中发现，第2 组划分数据无法重建哈夫曼树，因此未能通过校验，该划分错误；最后针对开头为000 的划分结果进行数据长度校验，亦未能通过，该划分错误。至此，只有第1 组数据划分结果通过所有校验，说明其为正确划分，通过该划分点将原始压缩数据划分后，前后两部分划分内容均可被独立处理。

图5 推测划分检验示意图Fig.5 Schematic diagram of speculative division evaluation

经过对推测划分数据的检验后，通过检验的划分依据才能真正将压缩数据划分成可独立处理的数据分块。再用这些通过检验的划分依据对压缩数据进行二次划分，这样的划分结果可以保证被独立解压缩，进而被用于并行解压缩。待二次划分结束，算法进入并行解压缩阶段。

2.3 并行解压缩

并行解压缩是算法的第三阶段，该阶段的目的是并行处理经过推测划分和推测检验的数据块集合。在该阶段，首先将经过二次划分的数据块集合传输到分布式计算框架的各计算节点中，同时设置相应的资源调度策略，以保证分布式计算框架能提供充足的算力，支持所有数据块的并行处理。在数据传输和资源调度之后，由主节点根据推测划分块的数量，派生相应数量的并行任务，同时对所有的分块进行解压缩。在该过程中，所有工作节点执行的任务内容相同，而处理的数据不同，每个节点内部的具体执行内容如算法2所示。

在并行解压缩阶段，分布式计算框架中的每个计算节点以动态哈夫曼树为参考，解压缩数据。具体流程是在读入编码数据时，按位逐个遍历哈夫曼树，得到的叶子节点信息即为该编码数据的解压缩结果。重复这个过程直到遇到块尾标号，再将所有遍历结果收集整合，得到压缩数据的解压缩结果。重复上述全部过程，直到经过推测划分的数据全部被解压缩，最终将全部解压缩结果按顺序合并，从而得到并行解压缩的其中一部分执行结果。

2.4 结果合并

当分布式计算框架中的所有节点完成解压缩任务后，算法进入结果合并阶段，该阶段由两部分组成：解压缩结果合并和出错处理。具体来说，如果所有节点的并行解压缩任务均顺利完成，那么这些结果将被汇总至分布式计算框架的主节点中，并按照输出数据的组织格式，顺序合并解压缩结果，形成并行解压缩的输出；如果解压缩过程出现问题，解压缩出错的节点需要上报错误信息给主节点，主节点则记录出错节点的位置，保存出错节点之前的所有解压缩结果，并抛弃出错节点之后所有的解压缩结果，将数据回滚，再重新对出错节点之后的所有数据按顺序用传统的数据解压缩算法重新解压缩，以保证最终输出结果的正确性。

3 算法实现

本文提出的算法通过推测划分数据再并行处理的方式，使原本按照压缩顺序串行处理的高速列车监测数据可以通过推测的方式并行处理，同时通过推测校验和结果合并机制保证推测执行结果的正确性，使算法兼具高效性和稳定性。为了详细描述算法，将选取高速列车实际运行数据作为研究对象，以Apache Spark为实现平台，对算法流程进行介绍。

研究对象数据选自2019 年4 月11 日西成高铁成都东至西安北的D1912 次列车所产生的监测数据，该列车采用8 辆编组，监测数据由CRH380BL车型的传感器产生，数据量约为19 GB，采用Zlib 编码标准进行压缩。表示算法在Apache Spark 上的执行流程的有向无环图（Directed Acyclic Graph，DAG）如图6～7所示：Apache Spark的主控制节点（以下简称主节点）从分布式数据库中读入监测数据，形成弹性分布式数据集（Resilient Distributed Datasets，RDD），并将监测数据存储为键值对的形式，其中键表示数据分块的顺序，值表示监测数据的二进制代码片段。

图6 推测并行算法执行的有向无环图1Fig.6 Directed acyclic graph 1 executed by speculative parallelism algorithm

按照算法设计，第一步为获取划分依据：指导集群中某单个工作节点解压缩监测数据RDD1 中的首个压缩数据块，解析动态哈夫曼树，获取块尾标号（在本示例中的值为10111），形成RDD2，接着对RDD1 进行持久化操作（图6 中的虚线部分），该操作的目的是备份RDD1，供推测检验结束后正确划分结果指导监测数据的重新划分。

第二步为推测划分，即使用块尾标号RDD2，对RDD1 中的所有元素进行并行划分，具体流程是以RDD2 中块尾标号为依据，按照32 MB 步长，对监测数据RDD1 中所有分片同时执行如图4 所示过程的划分，最终结果形成RDD3。在图6中，RDD1 经RDD2 划分后形成由M个分块组成的RDD3，在RDD3 内部，键值对与RDD1 的组成略有不同：键仍然表示分块顺序，值变为元组形式，其中，元组的首个元素代表划分位置相对于监测数据起始位置的偏移量，第二个元素代表划分结果。

第三步为推测检验，该流程类似图5 过程，即同时展开对RDD3 中包含划分结果的头校验、哈夫曼树重建和数据长度校验工作，并在检验结束后，形成由P个分块（P≤M）组成的推测检验结果RDD4，其内部数据组成形式与RDD3相同。

第四步，使用经过推测检验的RDD4 中所蕴含的偏移量，对RDD1 进行并行重划分，过程类似于推测划分，最终形成RDD5，在RDD5 的每个分块中，值代表经过重新划分，并可被独立处理的二进制代码片段。待重新划分结束，结果被继续存于各工作节点的本地空间，等待后续并行处理，推测检验阶段结束。

第五步为并行解压缩。如图7 所示，在该过程中，RDD5中的所有数据分块将遵照算法2 的流程同时进行解压缩，并行解压缩的结果将形成RDD6；待并行解压缩结束，再将结果合并，具体过程如下：所有RDD6 中的数据由各工作节点回传至主节点，再由主节点按照RDD6 中键值对的排列顺序，依据规定输出结果的文件格式类型，对所有结果按顺序进行合并，形成RDD7，最后将合并结果RDD7存回分布式数据库HDFS，完成推测并行解压缩算法的全过程。

图7 推测并行算法执行的有向无环图2Fig.7 Directed acyclic graph 2 executed by speculative parallelism algorithm

4 实验与结果分析

为全面测试推测并行解压缩算法的功能和性能。实验设计如下：在实验环境配置方面，选用7台相同配置的联想ST58小型塔式服务器，搭配Juniper J6350 企业级高性能路由器组建计算集群，并部署最新版本的Apache Spark 3.0.1。

实验数据随机选择成都铁路局下辖的4 列高速列车在2019 年4 月至6 月期间所产生的监测数据。数据使用Zlib 编码指导压缩，大小从20 GB 到200 GB 规模不等，用以测试算法在应对不同规模数据时的性能表现情况。测试数据的详情如表1所示，其中File 4记录的是同一列车往返的监测数据。

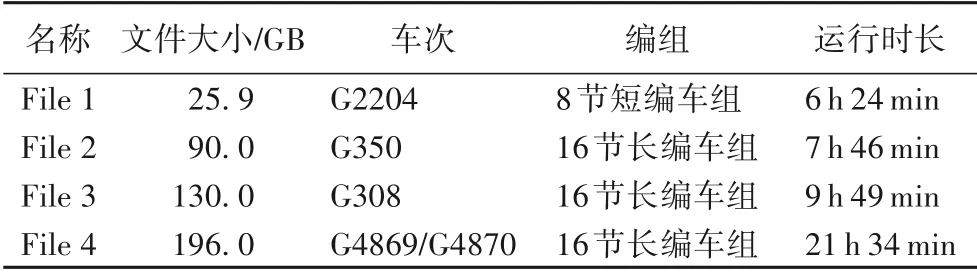
表1 实验数据集Tab.1 Dataset used in experiment

此外，为了探究算法的可扩展性，还设置了4 组对照实验组，分别是传统串行算法在Apache Spark 上串行执行，以及推测并行算法在由3/5/7 节点组成的集群上并行执行。实验方案和具体配置如表2 所示。值得注意的是，由于传统算法只能串行执行，因此即使分配再多的节点，算法实际使用的节点数仍只有2个，即1个主节点+1个工作节点。

遵照表2 设计的实验方案，分别对传统串行算法和推测并行算法进行测试。为保证实验结果的可靠性，每组实验在Apache Spark 上分别运行五次，求取平均运行时长作为最终实验结果。此外，在实验中使用开源的分布式监控系统Ganglia实时检测集群中所有节点的CPU、内存、磁盘、I/O负载以及整体网络负载情况。

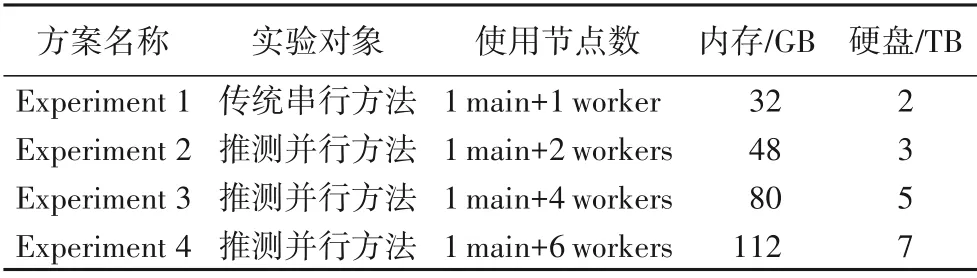
表2 实验方案的具体配置Tab.2 Specific configuration of experimental schemes

下面从性能、可扩展性、可靠性等方面对基于推测技术的并行算法进行测试评估，并结合实验数据，进行相关分析。

4.1 算法的性能测试与分析

首先测试推测并行算法的性能。图8 展示了在由7 个节点组成的环境下（实验方案Experiment 4），传统串行算法和推测并行算法的运行时长对比。如图8 所示，尽管两组实验的硬件条件相同，但是由于传统算法在Apache Spark 上串行执行，通过Ganglia 可以检测到在算法实际运行过程中，仅有一个主节点与一个工作节点参与有效计算，而基于相同环境的并行算法由于可以同时调度和使用集群所有资源，因此执行时间大幅缩短。

详细研究图8 可以发现，在由7 节点组成的集群下，针对大规模数据的解压缩过程中，并行算法在处理相同大小文件时，平均耗时比传统串行算法减少了约2/3。经过统计不同算法处理File1 到File4 的时长，可以计算出相较于传统算法，并行算法将解压缩的效率提高了2.10 倍。因此说明在面对大规模高速列车监测数据的解压缩时，基于推测并行技术的解压缩算法比传统串行解压缩算法更高效。

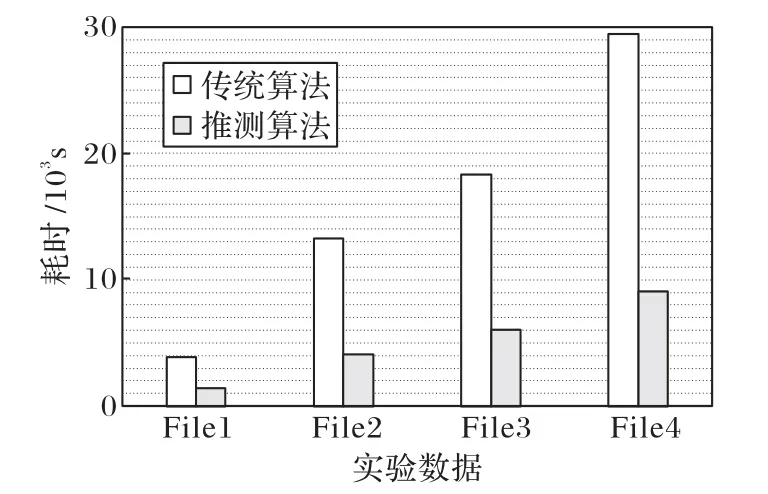
图8 性能测试结果Fig.8 Results of performance evaluation

4.2 算法的可扩展性测试与分析

为了测试算法的可扩展性，设计实验如下：在保持测试数据不变的情况下，逐渐增加集群中工作节点的个数，设置如表2 所示的三组实验方案对照组；再在这三组实验方案下，分别使用推测并行算法解压缩File1 到File4 的数据，并统计算法在不同方案中的执行时长；最后，通过观察算法的执行时长变化情况，验证算法是否具有良好的可扩展性。

图9 展示了在不同节点数的情况下，推测并行算法在处理同规模数据时的性能变化情况。面对相同规模的压缩数据时，随着节点数的增加，推测并行算法的执行时间逐渐减少。此外，由图9 可以看出，当测试数据增大到一定程度（大于100 GB），节点数量的变化对算法的性能影响更加明显。

图9 可扩展性测试结果Fig.9 Results of scalability evaluation

加速比计算公式如下：

其中：p表示可并行部分的占比；s表示处理器个数或可并行部分的加速倍数。

经过计算，推测并行算法在不同环境下处理相同数据时的加速比变化情况如图10 所示。随着节点数的增加，算法加速比S（p如式（5）所示）逐步上升，特别在针对大于100 GB 的大规模压缩数据的处理中，算法的加速比跟随并行机数量的增加呈近似线性增长。表明本文算法具有很强的扩展性，其性能随着工作节点数的增加而不断提升，进一步验证了图9所呈现出的实验结果。

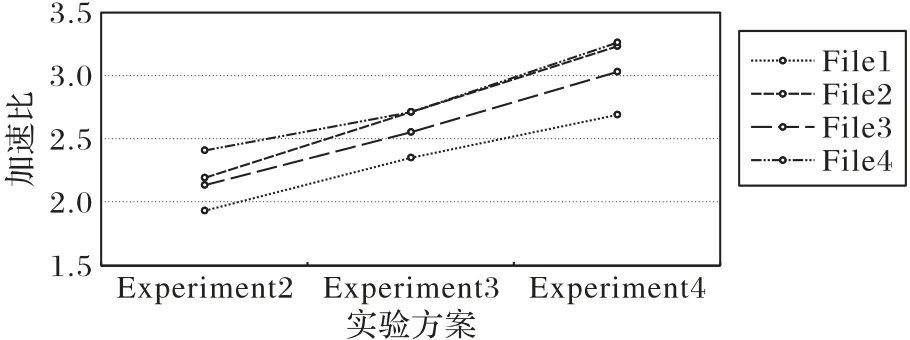
图10 各算法加速比变化情况Fig.10 Change of algorithms’speedup

4.3 算法的可靠性测试与分析

算法的可靠性，或称算法的准确性，是衡量算法是否优秀的核心要素。从本质上讲，推测并行算法是利用之前无法被串行算法充分利用的计算资源来进行额外计算，进而从额外计算的成功中获得性能提升，故其性能提升的基本原理是以资源换取效率，与基于多核架构的并行算法原理类似。因此，如果推测并行算法中的推测错误率太高，不仅表示算法的准确性差、可靠性低，同时会导致集群中大量计算资源被用于进行无效计算，严重时甚至影响算法的整体性能。

为了测试算法的可靠性，需要对推测划分结果的准确率做统计和分析，具体方法是：在对推测划分的结果进行验证结束以后，使用插桩测试技术，统计出现错误的推测划分数据的比例。结果如表3所示。

表3 错误推测率的统计Tab.3 Statistics on mis-speculation rate

按照32 MB 为最小划分步长对压缩数据进行推测划分，其推测划分块的数量如表3 的第三列所示。经过推测检验，发生误推测的数据块数量如表3 的第四列所示。从这两列数据内容可以看出，只有极少数的推测划分出现了错误。误推测的比例始终维持在0.5%以下。这意味着在本文算法中，只有极少量的资源被浪费在基于错误推测结果的计算上，而大部分计算资源被用于进行有效计算。这不仅意味着本文算法具有很强的可靠性，也说明本文算法能够充分有效地利用Apache Spark中蕴含的计算资源，避免资源浪费等问题。

4.4 对算法性能提升机制的分析

通过以上实验，证实了推测并行算法兼具高效性、可扩展性和高可靠性。在此基础上，为了深入了解算法性能提升的原因，以及探究影响和制约算法性能的因素，还需对推测并行算法性能提升的机制进行分析。具体方法如下：利用分布式监控系统Ganglia 统计推测并行算法在执行时各个阶段的耗时情况。为统计分析便利，将推测划分和检验阶段统称为推测准备阶段，各阶段耗时如图11所示。图11展示了在不同实验方案下，针对不同的测试数据，并行算法的分阶段执行时间统计。在推测并行算法中，推测划分、推测检验、并行解压缩3 个阶段为并行执行，而结果合并阶段为串行执行。反映在实验中，即如图11 所示，在面对相同的实验数据时，随着节点数的增加，推测准备和并行解压缩阶段的耗时不断减少，使算法保持了良好的可扩展性；然而，数据合并阶段不会因为计算资源的增加而减少，面对相同规模的数据，该阶段耗时基本保持不变。随着数据量的不断攀升，结果合并阶段所占时间比例也越来越大，甚至明显超过推测准备与并行解压缩阶段所用时间之和。同样地，随着集群中计算节点数的增加，算法在处理相同规模的测试数据时，推测准备与并行解压缩阶段用时逐渐减少，但结果合并阶段却不受其影响所占时间比例越来越大，反映在图10 中的表现为：随着计算节点数量的增加，算法整体加速比增长越来越不明显。因此结果合并阶段成为制约算法效率进一步提升的重要因素。究其原因在于推测准备和并行解压缩阶段是并发的，而结果合并阶段则是在主节点上串行进行的，随着计算节点的增加，算法的并行阶段耗时会越来越少，而结果合并阶段耗时基本不变，因而导致整体性能提升幅度越来越小。因此优化结果合并阶段将成为后续的研究重点。

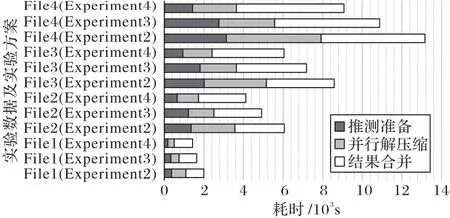
图11 本文算法各阶段耗时统计Fig.11 Statistics on time consumption of each stage of proposed algorithm

5 结语

本文提出了一种面向高速列车监测数据的并行解压缩算法，在暂时忽略数据依赖的前提下，使用推测并行技术，将采用变长编码技术压缩的、原本不可划分的高速列车监测数据进行试探性划分，再利用压缩数据的结构特点，对划分结果进行检验，在保证划分准确的基础上，并发处理划分结果，使原本只能按照数据组织结构串行进行的数据解压缩过程能够以推测的方式并行化进行，进而提高针对高速列车监测数据的解压缩效率。上述工作已经取得了良好的实际效果，通过与北京交通大学和中车唐山机车车辆有限公司合作，本文算法及相关产品已应用于包括CRH380BL 和CRH380B-002 等型号的高速列车监测记录数据的并行解压缩工作中，并提高了针对此类车型监测记录数据的分析效率，但通过实验分析可知，在该算法仍存在可优化空间，对于算法中的结果合并阶的优化将是今后研究工作的重点。