基于聚类分析的差分隐私高维数据发布方法

陈恒恒，倪志伟*，朱旭辉，金媛媛，陈 千

（1.合肥工业大学管理学院，合肥 230009；2.过程优化与智能决策教育部重点实验室（合肥工业大学），合肥 230009）

（*通信作者电子邮箱zhwnelson@163.com）

0 引言

随着大数据时代的全面到来，数据发布过程中的个人隐私面临更严重的威胁，如何做好隐私防护显得尤为重要。差分隐私作为一种可以对保护强度进行量化评估的隐私保护技术，无需考虑攻击者背景知识，在数据发布方面得到了广泛应用，逐渐成为隐私保护领域的一个研究热点［1］。现有研究对低维数据的发布问题作了诸多努力，但实际应用中高维数据的发布需求往往更为强烈，并且低维数据的隐私发布方法难以处理高维数据，直接加噪会导致数据可用性降低、查询结果敏感度增大等问题［2］。

针对高维数据的差分隐私发布，通常使用的方法是降维，利用有效的维度转换方法得到低维数据，再对转换后的低维数据集添加噪声，已有研究涉及阈值过滤技术［3］、随机投影［4］、主成分分析［5］、概率图模型［6-8］等方法。文献［3］基于阈值过滤技术选择部分属性达到降维目的，文献［4］通过随机投影技术学习原始数据集向量之间的L2 距离，文献［5］将主成分降维用于差分隐私数据发布，文献［6］利用贝叶斯网络来推理属性之间的关联关系，文献［7］基于Markov 网络构建属性集群，文献［8］采用隐树模型对高维数据的维度相关性进行结构学习，文献［9］利用组合原理选择低维视图构建低维加噪边缘表用于数据发布，文献［10］结合截断和分组两种技术以提高隐私数据发布结果准确性，文献［11］计算Copula 函数来描述多变量随机向量之间的相关性。此外，依据属性间关系假设的不同，高维数据发布方法又可分为数据独立的发布方法与数据相关的发布方法。文献［3-4］和文献［9-10］没有考虑到属性之间的依赖关系，属于数据独立发布方法。数据相关发布方法假设属性间相互依赖，现有研究多通过概率图模型判别属性间的关联性，如贝叶斯网络、Markov 网络，隐树模型或者其他判别属性间相关性的方法，如皮尔逊相关系数、卡方关联测试［12］等。

文献［6］提出的PrivBayes 方法是数据相关发布方法的典型代表，通过构建贝叶斯网络进行降维，更加容易保持属性间概率的一致性和完整性，在实现降维的同时较好保留原始数据的固有特征，因此许多研究在其基础上进行应用和改进。如：文献［13］构建了在本地化众包应用场景中的高维数据发布方法，文献［14］解决了分布式环境下的隐私发布问题，文献［15］提出了一种高维感知数据本地隐私保护发布机制，文献［16］提出了一种加权贝叶斯网络方法，文献［17］提出了一种基于语义树的贝叶斯网络隐私数据发布方法。然而，由于该类方法在构建网络时存在大量的候选属性对，会在降低指数机制选择精度的同时，带来大量的计算开销。此外，基于概率图模型的高维数据发布方法虽考虑了属性间关联关系，但是因其过高的计算时间复杂度往往只适用于小规模网络。

当前差分隐私研究的核心问题是提高发布数据的可用性及方法的计算效率，为了克服已有方法的不足，本文提出了一种基于聚类分析技术的差分隐私高维数据发布方法PrivBC，主要工作包括：

1）设计了一种基于K-means++的属性聚类方法，引入聚类的思想对贝叶斯网络进行分割，以缩减网络结构空间，降低方法计算复杂性，并减少隐私预算的分割次数，提高指数机制选择精度。

2）针对贝叶斯网络构建提出改进方法，为高效挑选出具有依赖关系的属性对，改进候选属性对的生成机制，采用基于关系矩阵的过滤技术来缩减指数机制的搜索空间，优化贝叶斯网络构建质量和效率。

1 相关工作

1.1 差分隐私

差分隐私保护模型的主要思想是，通过向待发布数据集或计数中添加适当噪声，以至于攻击者不能推断出某个记录是否在发布的数据集中，因此用户的隐私可以得到保护［18］。

定义1 相邻数据集［19］。设D={t1，t2，…，tn}为原始高维数据集，当且仅当数据集D'与D满足式（1）时，称D与D'为相邻数据集。

其中：D+tr表示将记录tr添加到数据集D后产生的数据集。基于相邻数据集给出ε⁃差分隐私定义如下。

定义2ε⁃差分隐私［19］。给定随机方法O，对于任意相邻数据集D和D'以及方法任何可能输出集合Ω，若方法O满足式（2），则称随机方法O严格提供ε⁃差分隐私保护。

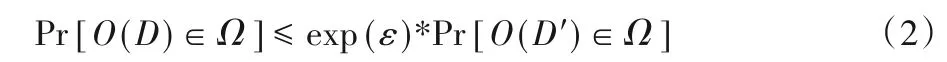
其中参数ε称为隐私保护预算，其值与方法的隐私保护强度成反比，值越小，保护程度越高。任何满足定义1 的机制都可以视为差分隐私，例如Laplace 机制通过向查询结果中添加Laplace 分布噪声来满足差分隐私，指数机制则通常用于输出为非数值型的方法。

定义3Laplace 机制［20］。对任意查询函数f：D→Rd，若方法A满足式（3），则称方法满足ε⁃差分隐私。

其中：Δf为查询f的全局敏感性；lapi(Δf/ε)为彼此独立的Laplace 噪声变量。由式（3）可知噪声量大小与Δf成正比，而与隐私预算ε成反比。

定义4指数机制［20］。设S为指数机制下的某个隐私方法，若其在打分函数F(ni)作用下的输出结果满足式（4），则称方法S满足ε⁃差分隐私。

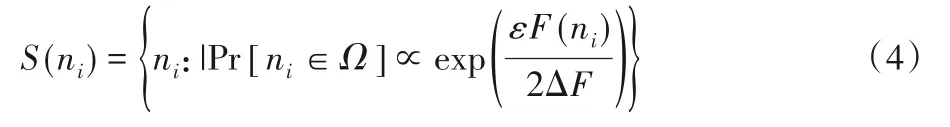
其中：ΔF为打分函数F(ni)的全局敏感性。由式（4）可知ni的打分函数越高，被选择输出的概率越大。

1.2 贝叶斯网络

贝叶斯网络N是一种较为常用的概率图模型，它借助属性节点间有向边来描述属性之间的依赖关系，能更加直观地表达属性间的条件独立性。具体来说，它由属性代表的节点ai和节点之间的有向边(ai，aj)组成，有向边代表着节点之间的依赖关系，并用有向边连接属性节点间的条件概率大小定量表示节点之间的依赖程度。假设属性对(ai)表示ai节点与其所有父节点的集合Πi，则对于给定的属性集合A和属性对集合(a，Π)，联合概率分布可表示为PA(a1，a2，…，ad)=。图1 表示包含5 个节点的贝叶斯网络，图中所有节点a1，a2，…，a5的联合概率可计算为：

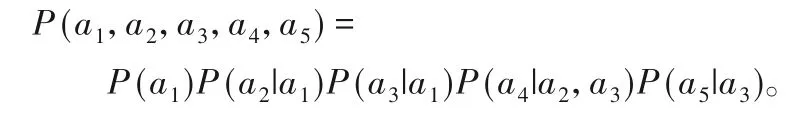
图1 含5个节点的贝叶斯网络Fig.1 Bayesian network with five nodes

1.3 最大信息系数

互信息是用于衡量两个属性间关联程度的常用指标，但对于连续型属性，互信息的计算结果对离散化的方式很敏感，且对于不同数据集计算出的结果无法比较。最大信息系数（Maximum Information Coefficient，MIC）［21］的提出可以解决上述问题。它以互信息和信息论为基础，采用网格划分的方法，可以更准确地识别出大数据集中属性间的线性或非线性关系，以及非函数依赖关系，具有普适性、公平性、计算复杂度低等特性。

定义5最大信息系数。给定属性X，Y和有序对，样本数量为n，将当前x⁃y平面划分为a×b的网格G，并使属性数据点都落入网格G中，定义属性X和Y的最大互信息计算式（5）如下：

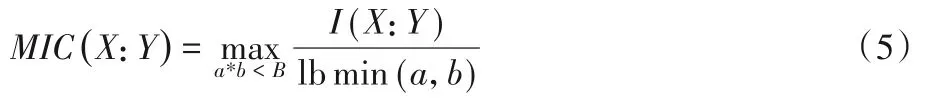
其中：B为网格划分a×b的上限值，通常取值为n0.6。

2 基于聚类分析技术的发布方法

2.1 PrivBC方法

PrivBayes 方法采用基于依赖统计分析的方法，在构建小规模网络时可以得到理想结果；但在面临大规模稀疏数据集时，方法的计算复杂性和网络结构复杂度都将呈现出爆炸式增长，这势必造成方法的可用性降低。文献［22］引入方法分团思想对动态贝叶斯网络进行分割，以降低抽样状态空间。文献［23］指出，针对高维数据的发布需要辅以对属性进行聚类或分组等方式进行降维。基此，本文针对属性之间的复杂关系，引入方法聚类的思想，提出基于属性聚类的贝叶斯网络隐私数据发布方法，首先计算高维数据属性之间的相关性，并对属性进行聚类，然后分别对具有不同内部相关性的子集簇使用贝叶斯网络作近似推理。

图2 展示了PrivBC 隐私保护方法的发布流程，具体由属性子集的聚类划分、加噪贝叶斯网络构建、加噪条件分布生成、合成数据集的发布四个阶段组成。其中二、三阶段分配的总隐私预算分别为ε1和ε2，其中ε=ε1+ε2。

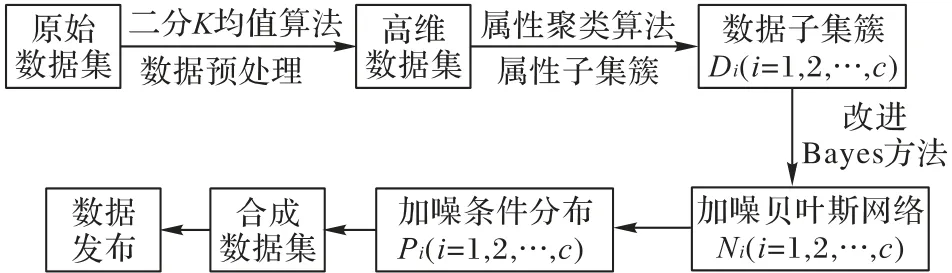
图2 PrivBC数据发布方法流程Fig.2 Flowchart of PrivBC data publishing method

特别地，设子集簇数量为c，每个子集簇根据拥有的属性个数占c个子集簇拥有的总属性个数比例分配隐私预算：

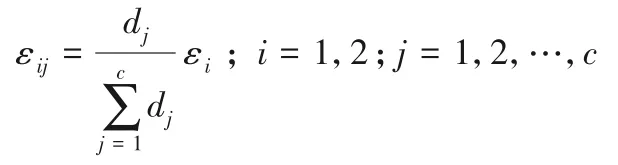
根据差分隐私的组合性质可知，PrivBC 方法满足ε⁃差分隐私。PrivBC方法四个阶段的概述如下。

1）属性子集的聚类划分：获取原始数据集，对于非二进制数据集中的连续型属性采用二分K均值方法进行个性离散化处理。随后计算属性之间的相关性，采用改进的属性聚类方法将高维属性集划分成c个属性子集，进而根据属性子集将原始数据集D划分成c个数据子集Di(i=1，2，…，c)。

2）加噪贝叶斯网络构建：对于聚类得到的每个数据子集，分别使用改进Bayes 方法构建加噪贝叶斯网络Ni(i=1，2，…，c)，使构建的每个贝叶斯网络满足ε1i的差分隐私。

3）加噪条件分布生成：对于加噪得到的每个贝叶斯网络，分别根据加噪联合概率分布计算加噪条件概率分布Pi(i=1，2，…，c)，使构建的条件概率分布满足ε2i的差分隐私。

4）合成数据集发布：根据网络结构N和加噪条件概率分布依次采样每个属性，生成扰动数据集(i=1，2，…，c)，根据此得到合成数据集D*，并将合成数据集进行发布。

2.2 属性聚类方法

区别于数据对象聚类方法，属性聚类方法旨在依据属性间相关性对属性进行聚类，使得同一簇中属性具有较高相似度。文献［24］提出的属性聚类算法（Attribute Clustering Algorithm，ACA）能较准确地对属性进行聚类，但实际应用中尚存在一些问题：一方面，ACA 采用K-means 方法随机选取初始聚类中心属性，存在很大的不确定性，最终导致聚类结果误差较大；另一方面，ACA 采用互信息度量属性间的依赖关系，需要通过联合熵对互信息值作归一化处理，对于连续型属性离散化的方式较为敏感。

针对K-means 方法存在的缺陷，诸多研究作了相应努力。如：文献［25］和文献［26］分别提出了精确加速方法YinyangK-means 和BallK-means，在减少距离计算次数的同时能获得更好聚类质量。在初始聚类中心的选取上，文献［27］基于聚类中心间距离应当尽可能大的原则，提出了K-means++方法，使方法可以获取全局最优结果，在聚类结果准确性上有较大提升。此外，最大信息系数能高效检测大数据集中不同类型维度间关联关系，无需归一化处理。因此，考虑到上述两点不足，本文借鉴K-means++方法原理选取初始聚类中心属性，并采用最大信息系数量化属性间关联程度，提出改进的属性聚类方法MACA（Maximum Attribute Clustering Algorithm），如方法1所示。

定义6相对依赖关系。给定任意两个属性vi和vj，定义属性之间相对依赖关系计算式为：

其中：MIC代表两个属性之间的最大信息系数。

定义7复合依赖关系。给定任意一个属性vi和属性集C={vj|j=1，2，…，m}，为衡量属性与属性集中所有其他属性的相对依赖关系，定义属性到属性集的复合依赖关系为各相对依赖关系之和。

为验证采用K-means++方法选择初始聚类中心属性，代替K-means 随机选取方法的效用性，以相互依赖关系度量的总和作为评分函数，在多个真实数据集上对比平均聚类结果。如图3 所示，各个数据集的评分函数值都有所提升，说明改进方法在一定程度上减少了聚类误差。在聚类数目k的选取上，给定高维数据集D和属性集合V，数据集的聚类数目可参考相互依赖度量的总和值进行选取；以NLTCS（National Long Term Care Survey）数据集为例，结合图4选取其最佳聚类数目为2，以ACS 数据集为例，结合图5 其聚类数目选取为3；此外，Adult和TPC-E数据集的聚类数目分别取2、3。

图3 MACA与ACA这两个属性聚类方法的聚类评分值对比Fig.3 Comparison of clustering scores of two attribute clustering algorithms called MACA and ACA

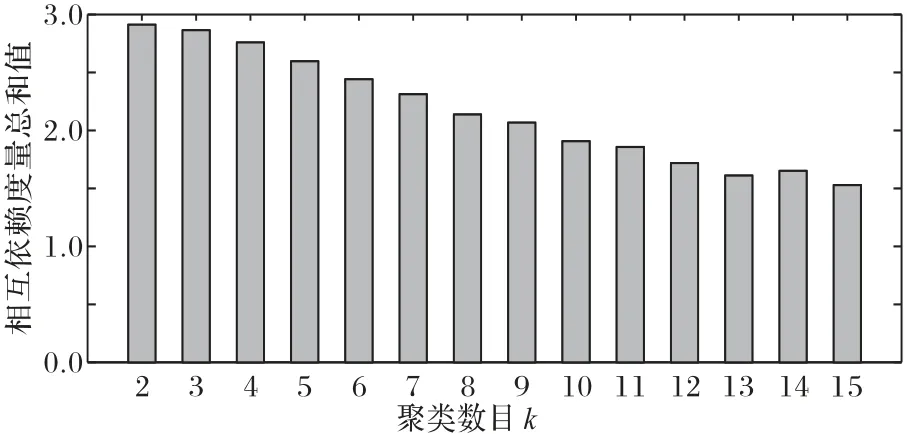
图4 不同聚类数目k在NLTCS数据集上的相互依赖度量总和值Fig.4 Total interdependence measure with different cluster number k on NLTCS dataset

图5 不同聚类数目k在ACS数据集上的相互依赖度量总和值Fig.5 Total interdependence measure with different cluster number k on ACS dataset

2.3 Bayes网络改进

PrivBayes方法在构建贝叶斯网络时为避免因过度访问数据集而产生大量噪声，采用贪婪方法选取属性AP（Attribute Parent）对，每次AP对的选取都需要全部计算候选属性集合中属性对的评分，弱相关性属性对的评分在节点选取中被重复计算，这无疑消耗了过多的计算资源。基于此，本文采用关系矩阵过滤技术来压缩候选空间，过滤掉Ω中弱相关属性对。

在前文计算出的V中每对属性节点间最大信息系数的基础上构造属性邻接矩阵M，确定每个节点vi的最大信息系数，记为MMIC(vi)，如果属性节点vi和vj(i≠j)之间的MIC(vi，vj)满足式（7），可知属性间相对依赖关系很弱，将其在邻接矩阵中的标识位设置为0，否则设置为1，据此得到属性间关系矩阵Rv。改进后的Bayes 构建如方法2 所示。对于PrivBayes 方法，未加入集合S的节点v都要计算与父节点Π的评分，循环共需计算d(d-1)/2 次，而，计算候选空间|Ο|=d(d-1)；对于PrivBC 方法，通过分析方法2 可知过缩减后的，候选空间|Ο'|=d(d-1)，因为|S'|<|S|，因此，方法运行效率得到提升。

2.4 方法复杂度分析

为更好说明方法可行性，有必要对方法复杂度进行理论分析。设D为高维数据集合，d为总属性维度，n为样本数量，c为属性聚类子集簇数目，v为子集属性维度。

方法的第一阶段使用K-means++方法聚类，时间复杂度为O(cdt)，t为迭代次数。第二阶段构建贝叶斯网络，考虑计算关系矩阵是一项独立的任务，时间复杂度为O(d(d-1))；此外，对于每个子集簇，需计算属性节点关联度，根据上文对候选空间的分析，加之网络构建循环需进行v-1 次，时间复杂度为，k为父节点个数，S'为缩减后每次循环的父节点集合，因此该阶段总时间复杂度为。第三阶段，构建加噪条件分布时每个子集循环需进行v次，时间复杂度为O(cv)。综上所述，PrivBC 方法总的复杂度为，由于v为子集属性维度，取值偏小，进而保证方法的优良性能。

3 实验与结果分析

3.1 实验设置

为了对PrivBC 方法的有效性和运行效率进行验证与说明，下面在真实高维数据集上开展具体的实验，从方法误差、方法有效性和方法性能方面与PrivBayes方法进行对比分析。

实验环境是Windows10 操作系统，Intel Core i5-6400 CPU（2.70 GHz），8 GB 内存。所涉及方法代码用Python 及Java 语言实现。实验所使用的4个数据集NLTCS、ACS、Adult、TPC-E均被广泛使用于高维数据发布。NLTCS数据集源自美国护理调查中心，包含了21 574名残疾人护理调查的记录；ACS 数据集源自IPUMSUSA 的ACS样本集，记录了从2013和2014年中获得的47 461 条个人信息；Adult 数据集源自美国人口普查中心，包含了45 222 条个人信息；TPC-E 数据集来自于某在线事务处理程序，记录了40 000 条事务信息。实验数据集的具体细节如表1所示。

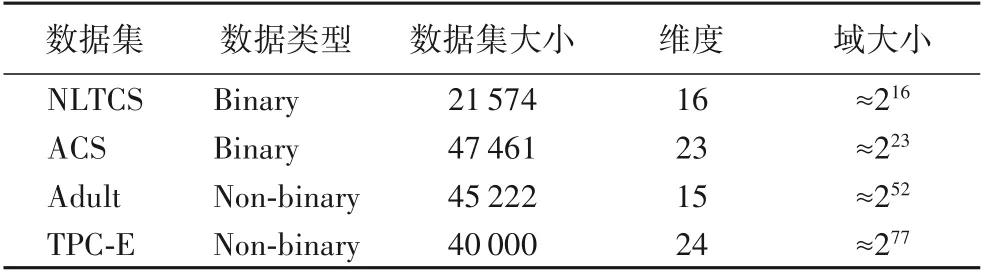
表1 4个数据集信息描述Tab.1 Description of four datasets

对于上述4 种数据集，隐私预算预算分配策略为ε1=0.3ε，ε2=ε-ε1，即隐私预算ε1=0.3ε用于构建加噪贝叶斯网络，剩余隐私预算用于产生加噪条件分布。特别地，当ε取值为0.05、0.1 时，ε1=0.1ε，ε2=ε-ε1。在Bayes 网络父节点个数k的取值上，对于NLTCS、ACS 和Adult 数据集，k默认取值3；对于属性维度更高的TPC-E数据集，k默认取值为2。

3.2 方法误差分析

为进一步评估加噪数据集的统计查询精度：对于二进制数据集，通过对比前后边缘表分布的L2错误距离来对发布数据的误差进行评估；对于非二进制数据集，参照文献［2，6］，通过对比加噪前后边缘表2-way 以及3-way 的平均变量距离（Average Variable Distance，AVD）来衡量方法查询结果的准确性。其中AVD 为加噪前后边缘表分布L1 距离的一半

图6（a）和图6（b）分别对比了二进制NLTCS、ACS 数据集在隐私预算ε为0.1 和1.0 时PrivBC 方法与PrivBayes 方法的L2 错误距离，其中纵坐标是对数刻度，可以看出在绝大多数情况下，PrivBC 方法的准确度都得到了较大提升，只有在ACS数据集上ε=1.0 时，PrivBC 方法准确性较PrivBayes 方法有稍许降低，但考虑到此时L2 误差都比较小，降低的查询精度在可接受范围内，此外，当聚类误差较加噪误差足够小时，该方法可以实现发布数据效用性及方法计算效率之间的良好折中，因此这表示为可接受的折中方案。

图6 二进制数据集上的L2错误距离Fig.6 L2 error distance on binary datasets

图7（a）和图7（b）分别对比了非二进制Adult 和TPC-E 数据集在不同隐私预算下的2-way、3-way 查询误差。由图7 可知，在隐私参数相同时，PrivBC 平均变量距离小于PrivBayes，即便在数据维度很高的TPC-E 数据集上，PrivBC 方法同样可以得到更好的精确度，尤其在隐私预算紧张时改进效果更加显著。这是因为PrivBayes 方法候选空间的大小会随属性的增加呈指数上升，造成隐私预算急剧减小，导致数据误差偏大，而PrivBC 方法由聚类形成的各个子集簇属性数量较少，网络结构简单，大大减少了计算属性对数量，从而保证良好数据效用。

图7 非二进数据集上k-way查询误差Fig.7 k-way query error on non-binary datasets

3.3 方法有效性分析

为了对发布数据的有效性进行分析，参考文献［4，7］选取NLTCS 和Adult 数据集，以加噪合成数据集的80%作为训练集，20%作为测试集，在通过PrivBC、PrivBayes 方法产生的加噪合成数据集上构建分类模型。优秀的分类方法有文献［28］的基于完全随机森林的类噪声滤波学习（Complete Random Forest based class Noise Filtering Learning，CRF-NFL）方法和文献［29］的粒球支持向量机（Granular Ball Support Vector Machine，GBSVM）、粒 球K近 邻（Granular BallK-Nearest Neighbors，GBKNN）方法等，这里参考文献［2，4，6］选取支持向量机（Support Vector Machine，SVM）方法构建分类模型。图8 展示了不同数据集上方法基于参数ε变化的平均误分类率，在NLTCS 数据集上，依据某个人：（a）是否能够外出（如图8（a）中Y=Outside）；（b）是否能够游泳作为分类属性作出预测。在Adult数据集上，依据某个人：（c）是否为男性；（d）是否结婚作为分类属性作出预测。其中PrivBR 方法为经过候选属性对缩减处理的PrivBayes 加噪方法，PrivateERM［30］方法通过对风险函数添加噪声并优化扰动来输出SVM 分类器，NoPrivacy在不加噪原始数据集上直接构建分类器。

图8 不同数据集上的SVM误分类率Fig.8 SVM misclassification rate on different datasets

从图8可以发现，对比PrivBayes方法，PrivBR方法在NLTCS 数据集上的属性误分类率有所降低，这表明缩减候选属性对空间能一定程度上优化所构建的贝叶斯网络。此外，可以观察到本文提出的PrivBC 方法的误分类率在绝大部分情况下小于PrivateERM 方法，并在很大程度上小于PrivBayes方法，特别在二进制NLTCS 数据集上，PrivBC 方法即使在隐私预算很小时也能达到较高精度。平均来看，PrivBC 相较于PrivBayes 方法的误分类率降低12.6%，这表明PrivBC 方法在有效保证数据隐私信息的同时，SVM分类精确性也有所提高，增强了数据发布效用。

3.4 方法性能分析

发布加噪数据集所需运行时间也是衡量隐私保护方法优劣的一个极其重要的指标。图9 对比了相同隐私预算条件下（如ε=0.8），贝叶斯网络的度k=2，3 时，四个高维数据集上，PrivBC 方法与PrivBayes 方法在发布加噪数据集时的运行时间。从图9 可看出，PrivBC 方法在NLTCS、ACS 维度较低数据集上，运行时间相较PrivBayes 方法没有优势，但在Adult、TPC-E 维度较高数据集上，PrivBC 方法运行时间明显短于PrivBayes 方 法，如 在k=2时，Adult数据集上PrivBC方法是PrivBayes 方法的1/3 左右，在TPC-E 数据集上为1/4 左右。此外，随着贝叶斯网络度k增大，PrivBC 方法运行时间的优势更加显著。这是因为，随着属性个数的增加，PrivBayes方法的计算复杂度呈指数递增，而PrivBC 方法的时间复杂度为每个低维子集簇计算时间的线性问题。平均来看，PrivBC 相较于PrivBayes 方法的运行时间降低30.2%（因k较高时，PrivBayes方法运行TPC-E 数据集因复杂度过高易造成内存溢出，计算时排除该数据集）。

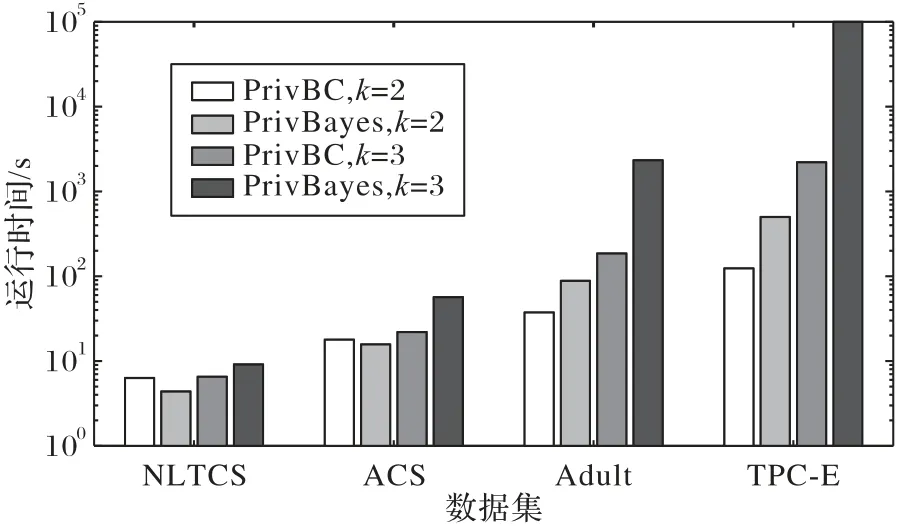
图9 不同数据集上方法运行时间Fig.9 Algorithm running time on different datasets

图10 比较了4 个隐私方法PrivBC、PrivBayes、PrivateERM和PrivLocal［31-32］在Adult 数据集上构建SVM 分类器的运行时间。PrivBayes效率最低，其次是PrivBC、PrivateERM 和PrivLocal。这是因为PrivateERM 和PrivLocal 直接输出分类器，而PrivBC 是一个生成合成数据集的通用框架，支持多个分析任务，这对于许多实际应用十分重要。

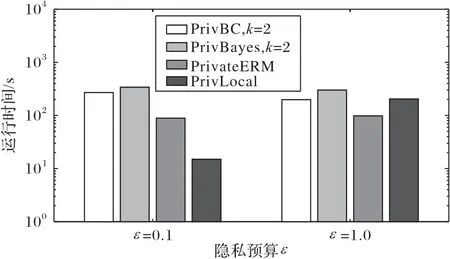
图10 基于SVM分类的不同方法在Adult数据集上的运行时间Fig.10 Running time of different algorithms based on SVM classification on Adult dataset

4 结语

针对PrivBayes 方法指数机制选择精度低，计算效率不足的问题，本文提出了一种基于聚类分析技术的隐私数据发布方法PrivBC。在构建贝叶斯网络时辅以聚类分析以及基于关系矩阵过滤冗余候选属性对，缩减了网络结构空间，减少了隐私预算分割次数。同时，改进连续型属性编码方式，提高了数据集的可用性。实验结果表明，PrivBC 方法能很好地兼顾加噪数据发布精度和发布时间，与PrivBayes 方法相比，其在发布数据查询误差、数据有效性和方法运行时间等多个方面性能都有显著提升。由于PrivBC 方法假设所有属性关系都是有向的因果关系，这与高维数据真实的属性关系存在差异；此外，由于方法需要计算属性对依赖关系，相较于属性独立发布方法计算时间开销较大。下一步可考虑将聚类思想与其他概率图模型相结合，采用Mapreduce 等编程模式实现方法并行化，应用于更多高维数据发布场景，如高维动态数据流的隐私发布。