一种火箭子级残骸六自由度落点预报方法

龚秋武 陈鼎 李翔 黄宇

（1 中国酒泉卫星发射中心，酒泉 732750）

（2 中国人民解放军95983部队，酒泉 732750）

0 引言

航天发射任务中，火箭子级、整流罩等残骸的搜索回收关系到地面人员、建筑和设备等的安全，必须严加防控，严密组织，严格执行，确保不伤人员，不损建筑，不毁设备。

而残骸搜索任务的前提就是要准确计算残骸的落点，以便在发射任务实施前做好危险区防控和人员疏散，任务实施时引导搜索人员和车辆等前往安全目标点。关于落点预报，国内外学者做了许多研究，如：文献[1-3]在载人飞船返回舱落点预报理论的研究中，考虑了地球自转、高空风以及其他摄动因素对落点精度的影响；文献[4-9]对弹道导弹落点预报进行了研究，包括轨道外推、气动力系数辨识、地球引力摄动等计算方法；文献[10-17]研究了火箭残骸的落点预报与控制算法；文献[18-20]研究了滤波算法在残骸落点预报上的应用。上述这些研究，都是基于质点的动力学模型，并未考虑返回器的姿态运动，而对于高空坠落地面的物体，姿态变换会影响其迎风面，改变其所受的气动力，进而干扰质心运动，影响最后的落点精度。

本文在质心运动的基础上，考虑火箭子级残骸的姿态运动，分析地球引力摄动以及气动力的影响，推导建立质心运动与姿态运动方程，对火箭子级残骸进行落点预报。

1 运动过程及受力分析

1.1 运动过程

火箭子级在完成推力任务时，在指令控制下与火箭主体或者载荷分离，由于飞行程序的不同，各子级分离时的位置与姿态也各不相同，但是基本的物理过程却是一致的。

一般火箭一、二子级和整流罩分离时的飞行高度较低，飞行速度还未达到绕地飞行最小速度，所以会在分离后很短的时间内坠落地球。火箭三子级和更上面的部分在分离时已经进入空间环境，速度也达到了绕地飞行的基本条件，因而这些部分会在太空绕地飞行一段时间，由于它们处于无控状态，不能进行轨道保持和控制，一般绕地飞行数圈后便坠入大气层被烧蚀掉。

坠落地球表面的火箭一、二子级和整流罩的着陆过程大致分为三个阶段：1）减速上升段，此阶段子级借助分离时向上的速度分量继续向上飞行，由于受到地球引力和大气作用力的影响，向上的速度分量逐渐减小至零，因而做减速上升运动；2）加速下降段，此阶段在地球引力的作用下，子级加速下坠，大气作用力随着子级速度的不断增大而增大；3）平衡段，此阶段子级受到的地球引力与大气作用力基本平衡，子级以一个相对稳定的速度下坠直至坠落地面。

1.2 受力分析

残骸在下坠过程中，一般处于无控状态，主要受到地球引力和大气作用力的影响。本节即对子级残骸受到的两种作用力进行分析。

1.2.1 地球引力

由于地球是非标准球体，为提高地球引力的描述精度，须将地球引力分为中心引力和非球形摄动力两部分。其中，中心引力的加速度为

式中 GME为地球引力常量；r为残骸质心的地心系位置矢量，r为地心距，其中X、Y、Z为地心系位置坐标。

地球非球形引力摄动加速度为地球非球形引力位的梯度，即

式中U为地球引力位，为缔合勒让德多项式，φ为目标点位的纬度，λ为目标点位的经度，为引力位田谐系数，RE为地球平均半径。

从而地球引力加速度g可表示为中心引力加速度g0与地球非球形引力摄动加速度g0′两部分之和，即

1.2.2 大气作用力

火箭残骸在下坠过程中，大气作用力影响很大，一方面气动力影响残骸质心运动，另一方面气动力产生的气动力矩影响残骸姿态运动。

（1）气动力

残骸受到的气动力如图1所示。

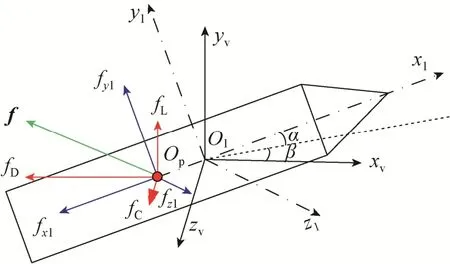
图1 残骸所受气动力Fig.1 Aerodynamic force of rocket wreck age

图1中O1-x1y1z1为弹体坐标系，O1-xvyvzv为速度坐标系，f为气动力合力，O1为残骸质心，Op为压心。为便于计算，可将气动力分解到弹体坐标系或者速度坐标系。当分解到弹体坐标系时，可得到轴向力fx1、法向力fy1和横向力fz1；当分解到速度坐标系时，可得到阻力fD、升力fL和侧力fC。根据气动力与飞行速度、大气密度等参数的关系，可计算得到气动力的大小为

式中0ρ为大气密度；Sr为残骸参考面积，一般取截面积；C为气动力系数；v为残骸相对于大气的速度，而非自身飞行速度，这里主要考虑高空风的影响。一般地，高空风数据通过气象测站释放的探空气球测得，数据格式为对应高度处的风向和风速，风向以当地正北为0°，顺时针方向至360°。假设某高度处的高空风风向为αW，风速为vW，其在测站坐标系中的速度矢量为

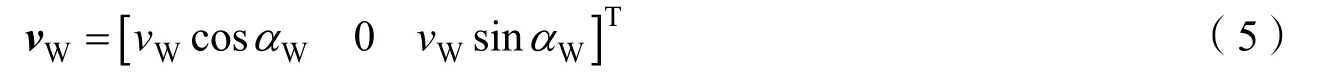
经过坐标转换，可将式（5）所示的高空风在测站坐标系的速度转换到发射坐标系，进而得到发射系中残骸相对于大气的速度，即

式中vG为残骸在发射系中的速度矢量；GE为地心坐标系到发射坐标系的转换矩阵；EC为测站坐标系到地心坐标系的转换矩阵。以上坐标系的定义可参考文献[21-23]，转换矩阵GE和EC的计算公式分别为：

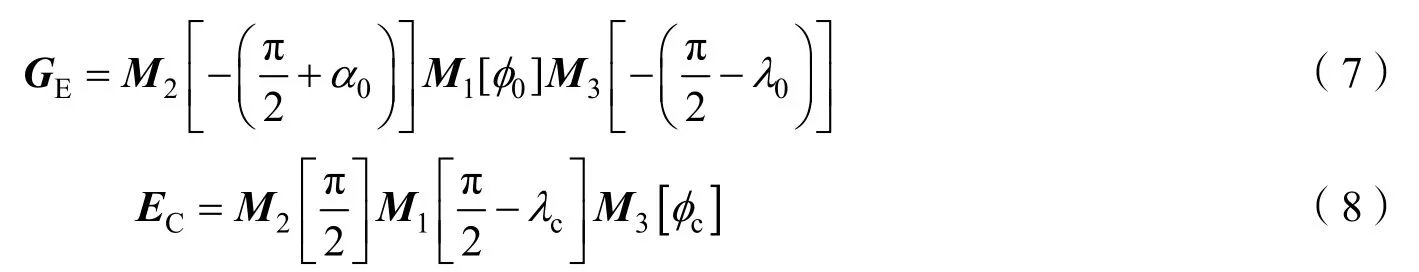
其中，0α为发射方位角；0λ为发射点经度；0φ为发射点纬度；M1、M2和M3为初等转换矩阵，具体定义和表达式可参考文献[21]；cλ为测站点位的经度；cφ为测站点位的纬度。

（2）气动力矩

由于气动力作用点在压心Op，而压心一般不与质心重合，所以火箭残骸受到的气动力会对残骸质心产生气动力矩，如图2所示。图2中rp为压心Op的位置矢量。

图2 残骸所受气动力矩Fig.2 Moment of aerodynamic force

假设弹体为静稳定的，用气动力矩系数来表征气动力矩，进而可将气动力矩表示为

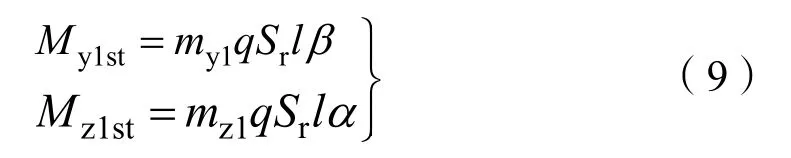
式中My1st为偏航力矩；Mz1st为俯仰力矩；my1为偏航力矩系数；mz1为俯仰力矩系数；q为动压，l为残骸特征长度；α为攻角；β为侧滑角。由于压心与质心一般均处于弹体轴线上，所以气动力不产生滚转力矩，即Mx1st=0。

2 动力学建模

2.1 质心动力学模型

残骸在坠落过程中任意时刻的质心运动状态如图3所示，其中OE-XEYEZE为地心赤道坐标系（简称地心系），OE为地心，OG-xyz为发射坐标系，OG为发射点，Rwc为残骸质心在发射系中的位置矢量、Rfp为发射点的地心系位置矢量，残骸质心的地心系位置矢量r=Rfp+Rwc。

图3 质心运动Fig.3 Motion of barycenter

根据运动学知识，对位置矢量求绝对导数即得到速度矢量，对速度矢量求绝对导数即得到加速度矢量a，整理得到

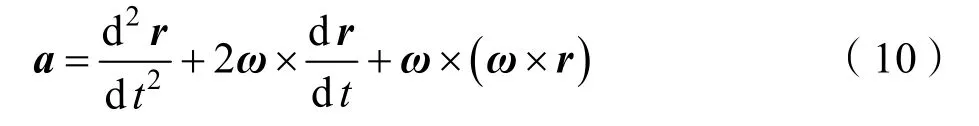
式中ω为两坐标系之间的相对转动角速度矢量。

假设残骸质量为m，结合前面的受力分析，则根据牛顿第二定律，可得到矢量形式的质心动力学方程

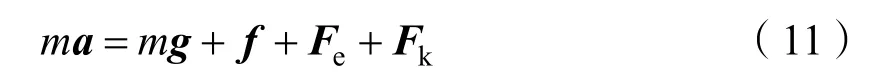
式中f为气动力；Fe为牵连力，为科氏力，Fk=-mω×（ω×r）。

矢量形式的动力学方程无法进行积分运算，还需选定计算坐标系，将其转换为标量形式的方程，此处以发射坐标系作为计算坐标系，将加速度和各力向各轴进行分解后便可得到标量形式的方程组。

2.2 姿态动力学模型

如前所述，残骸坠落过程的质心动力学方程中，含有欧拉角参数，并且将矢量形式的动力学方程转换为标量形式的动力学方程组时，涉及到力、加速度的分解，同样也含有欧拉角参数，而质心动力学方程是无法解算角度信息的，所以除了分析质心动力学外，还要考虑姿态动力学问题。如图4所示，O1-x0y0z0为惯性系，弹体系O1-x1y1z1相对于惯性系的姿态角分别为俯仰角φ、偏航角ψ和滚转角γ，对应的姿态角速度为φ˙、ψ˙和γ˙。

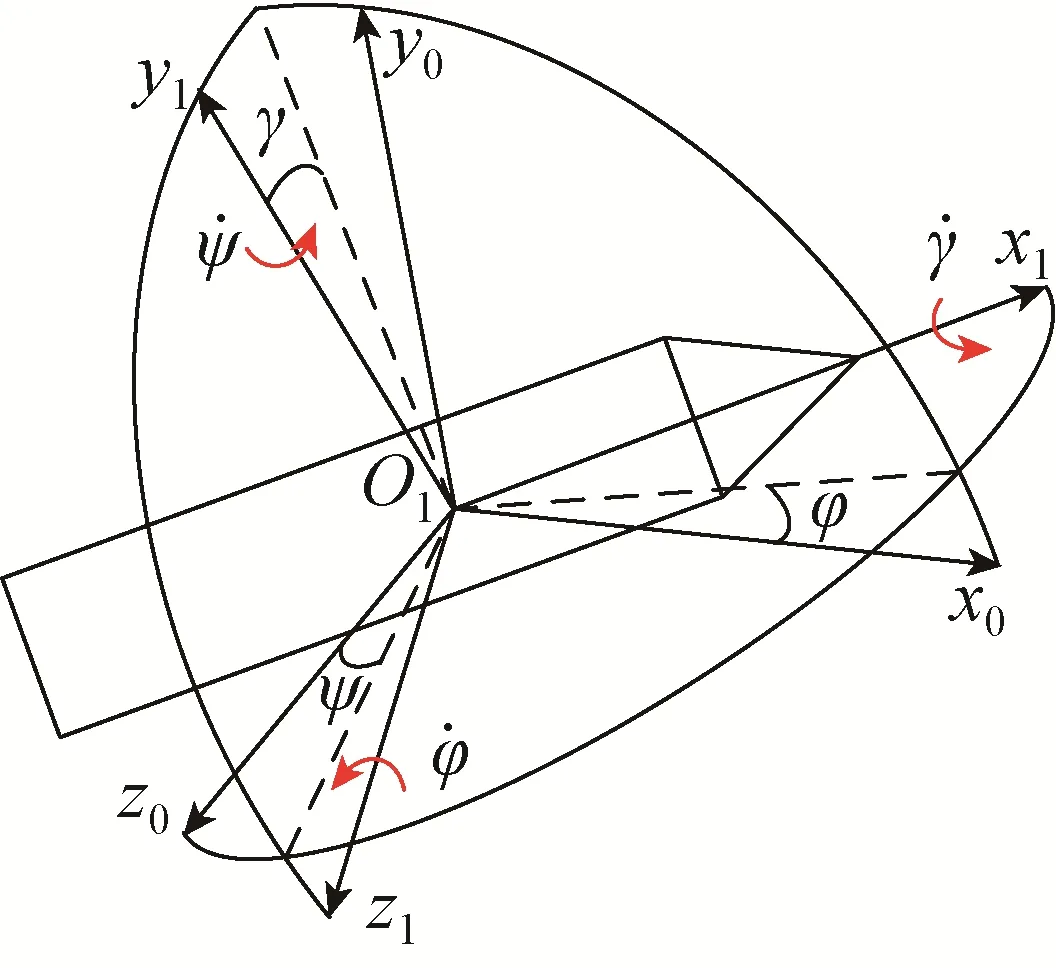
图4 残骸姿态运动示意Fig.4 Attitude motion of racket wreckage

根据姿态动力学理论，可得到姿态角速度与姿态角之间的关系，以及矢量形式的姿态动力学方程，即

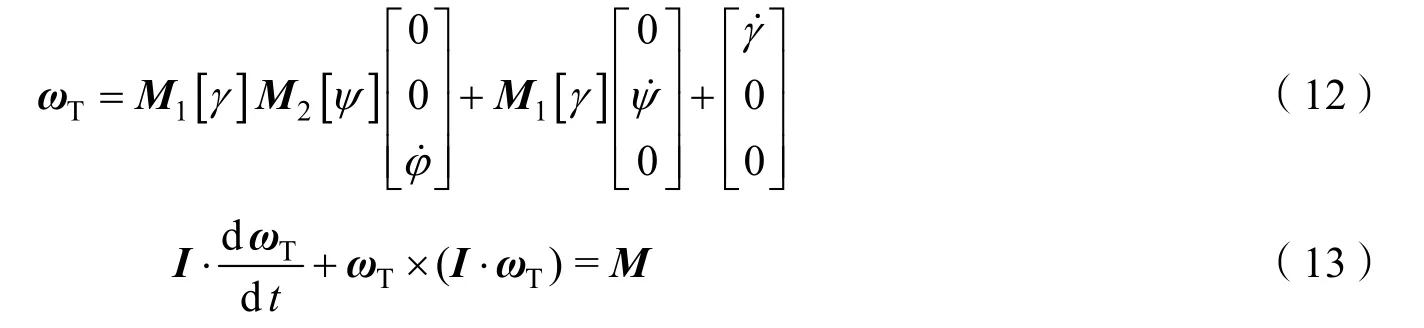
其中，ωT为体坐标系下的姿态角速度矢量，为残骸的惯量张量（假定残骸为轴对称体），其中Ixx、Iyy和Izz分别为残骸绕体坐标系三个坐标轴的转动惯量；M为残骸受到的合外力矩矢量。

由于残骸处于无控状态，控制力矩为零，另外阻尼力矩、附加科氏力矩和附加相对力矩是小量，忽略不计，最终残骸受到的合外力矩只考虑气动力矩，对于静稳定弹体则为稳定力矩。

选定弹体坐标系为计算坐标系，将矢量形式的姿态动力学方程转换为可积分运算的标量形式方程组。

3 数值仿真

以某次航天发射试验任务为例，对本文提出的落点预报方法进行仿真验证，地球参数参考文献[21]，发射点位参数、一子级残骸参数以及残骸分离点参数分别根据实际数据设置，高空风采取插值得到。将上述相关参数带入到建立的动力学模型中，利用四阶 Runge-Kutta积分算法进行数值积分，得到残骸从分离点到落地的三维弹道轨迹、飞行速度、飞行姿态角和姿态角速度等仿真结果（如图5～9所示），残骸预报落点与实际落点误差见表1。

表1 残骸预报落点与实际落点误差Tab.1 The error between the prediction falling point and real falling point

图5 残骸三维轨迹Fig.5 Three dimension trajectory of rocket wreckage

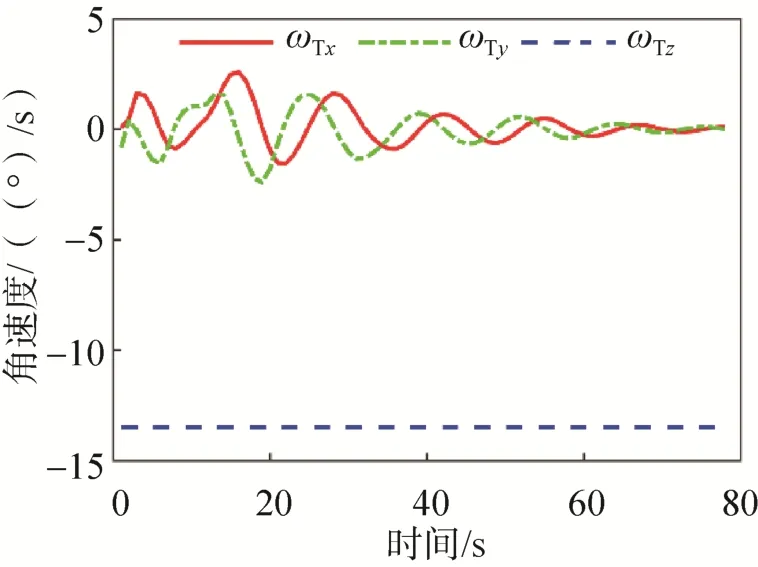
图8 残骸姿态角速度变化曲线Fig.8 Attitude rate curves of rocket wreckage

分析图5所示的仿真轨迹及实际落点并结合表1和图9，可以看出预报落点与实际落点相差很小，在高度 18km位置处进行落点预报得到的预报落点与实际落点之间的射向偏差约为 1.2km，横向偏差约为0.1km，射向和横向偏差均小于2km，以预报落点为圆心，2km为半径，得到的搜索范围约占工业部门提供的理论落区范围的10%；由图6可知，残骸下坠过程中，在地球引力和气动力的共同作用下，残骸先减速后加速，再减速至相对稳定；观察图7～8残骸姿态变化的仿真结果可发现，残骸的俯仰角φ逐渐减小至负方向至稳定，偏航角ψ在下坠过程中呈规律性波动，由于未考虑滚转力矩，滚转角γ以初始滚转角速度持续滚转。还可以看出，因为残骸是静稳定的，所以姿态角速度ωTy和ωTz维持在相对稳定的状态。

图6 残骸速度变化曲线Fig.6 Velocity curves of rocket wreckage

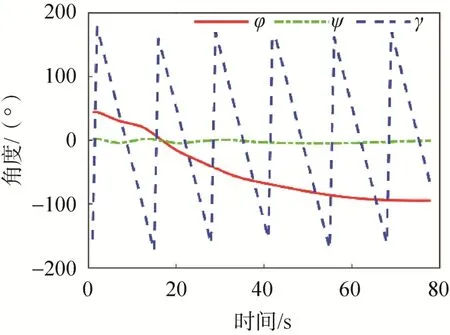
图7 残骸姿态变化曲线Fig.7 Attitude curves of wreckage

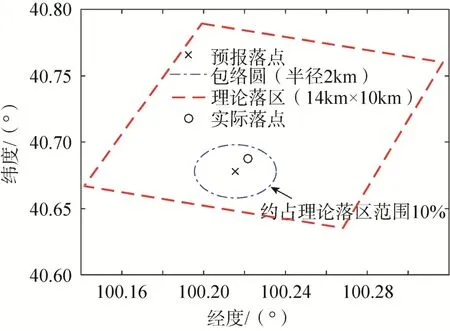
图9 残骸落点与落区Fig.9 The falling point and falling area of rocket wreckage

4 结束语

火箭残骸的姿态运动对质心运动具有一定的影响，进而影响残骸飞行轨迹和最终落点，因而本文在质心运动的基础上，对姿态运动进行了建模，进而提出一种火箭子级残骸六自由度落点预报方法，通过数值仿真，计算得到了某次航天发射任务中一子级残骸的坠落轨迹和各时刻的位置、速度和姿态等状态参数，还计算得到了残骸的预报落点。对比实际落点，预报落点的射向和横向偏差，均在2km以内，对比工业部门提供的理论落区，搜索范围缩小了约90%，增强了搜索的针对性，提升了搜索效率。