卫星TDICCD相机非沿轨成像仿真方法

岳庆兴

（自然资源部国土卫星遥感应用中心，北京 100048）

0 引言

灵活的成像方式是遥感卫星先进性的重要标志，文献[1]指出灵巧卫星需要解决的核心技术主要包括卫星的精密姿态控制、小像元尺寸和高积分级数TDICCD的研制，小相对孔径光学系统的设计以及用于图像增强的数字图像处理技术等。灵巧成像依照实现难度可以分成不同的等级，如侧摆成像是多数卫星都具备的较低级别的“灵活”，而同轨多视角立体成像、单轨大区域多条带成像、与星下点轨迹呈较大角度成像则是难度较大的“灵活”。我国的遥感卫星影像与法国Pleiades、美国WorldView等卫星影像相比较，存在影像“方向”的差异：Pleiades、WorldView卫星影像往往接近“正南正北”，体现了成像角度的灵活性，而我国遥感卫星影像一般是沿轨道倾斜的；另外，Pleiades和 WorldView卫星均可实现单相机同轨多视角立体成像，而我国卫星立体成像以同平台多相机模式为主，少数卫星虽具备单相机同轨立体成像模式，但其总体性能还有一定的差距。实现灵巧成像不仅是平台姿态控制的问题，其难度还与搭载的相机类型有关：如框幅式相机两次“成像”间的关联性较少，姿态因素对影像清晰度的影响较小；而 TDICCD相机需要对“同一”地面目标多次“成像”并“累加”，需要对像移速度和方向进行严格控制，使得同一列的多级 CCD依次严格对准同一目标，否则会出现成像模糊。虽然已有研究人员对卫星TDICCD相机成像进行了理论研究和仿真试验，但大多局限于卫星姿态控制或相机设计领域[2-6]，主要是TDICCD相机成像品质的影响因素或TDI积分成像对像移的要求[7-14]，相关数学建模一般以卫星动力学和运动学方程为基本出发点[15-17]。本文则以摄影测量中心投影的概念为出发点[18-20]，根据初始成像条件下TDICCD两次的像点“误差”，计算积分时间的修正量和保持正确像移方向的姿态运动方法和速度，实现了两种非沿轨方向TDICCD相机成像仿真：一是影像行地面投影与纬线方向接近的“正南正北”成像仿真；二是扫描方向与星下点轨迹方向呈一定角度的“摆扫”成像仿真。实现TDICCD相机非沿轨成像仿真的重点是在卫星的轨道参数、相机参数、初始积分时间和成像目标等基本参数已设置的条件下，确定卫星姿态的计算方法，包括初始姿态的计算和姿态运动速度的计算。本文论述了上述两种成像仿真涉及的姿态计算方法，以1∶1万数字高程模型（Digital Elevation Model，DEM）和1∶1万数字正射影像图（Digital Orthophoto Map，DOM）作为物方输入数据，在DOM上加入如图1所示的黑白靶标，用于分析多级积分条件下的成像清晰度，进而验证仿真方法的正确性。

图1 仿真输入靶标Fig.1 Input targets for simulation

1 仿真参数设置与初始姿态计算

1.1 参数设置

基本仿真参数包括轨道参数、相机参数、初始积分时间、成像目标。

轨道参数：轨道高度500km，轨道倾角97.5°，假设轨道为圆轨道，即偏心率为0。用随时间变化的卫星本体坐标系原点位置P(t){Xt,Yt,Zt}、速度V(t){VXt,VYt,VZt}向量序列作为轨道数据。同时，本文假设相机像空间坐标系原点与卫星本体坐标系原点重合，原点就是卫星的瞬时位置P(t)。

相机参数：焦距7.5m，CCD尺寸7μm，积分级数48级，主点坐标(r0,c0)为(0, 0)。

初始积分时间：根据卫星飞行速度、轨道高度、概略分辨率计算。

成像输入包括目标区域中心坐标M(X,Y,Z)，确定成像方向的辅助点M1(X1,Y1,Z1)，即主点会首先对准M1，M和M1坐标基准均为地心直角坐标系。经过一段时间后对准M，成像时长Tall。

1.2 初始姿态计算

在上述条件下，根据摄影测量中心投影原理，卫星在t时刻运行到位置P(t)“对准”目标M成像，可描述为M点“投射”到像面上的像点坐标为主点坐标(0, 0)，这个“投射”所用共线方程里的未知数是旋转矩阵R的9个参数；也可描述为像主点对应的像空间向量u[0, 0,-f]T（f为相机焦距）经旋转矩阵R旋转到物方向量u′，出发点为P(t)时u′与地面的交点为目标点M。两种方法的核心都是确定旋转矩阵R，本文基于后一种描述方法即向量旋转的方法计算矩阵R。

用整数秒时刻的卫星位置、速度描述卫星运行轨迹。P(t)时刻的位置、速度向量由t前后多个整数秒时刻的位置、速度通过拉格朗日插值获取。根据P(t)时刻的归一化位置、速度向量及二者的叉积计算瞬时轨道坐标系到地心直角坐标系的旋转矩阵Robt-eth。假设像空间坐标系与卫星本体坐标系重合。将像主点对应像空间向量经Robt-eth旋转得到物方向量u1，假设P(t)与目标点M连线向量为u2，像主点“对准”星下点的前提下再“对准”目标点所需矩阵为Rrth-obj，该矩阵通过u1和u2计算。假设u1和u2都已进行归一化，u1与u2的叉积为u3，u1、u2间的夹角θ通过反余弦公式求得。已知旋转轴u3和旋转角θ，可以通过四元数法计算Rrth-obj。

假设R=Rrth-obj×Robt-eth，通过R即可实现t时刻对准目标M成像，通过绕u2向量轴旋转一定角度k还可以改变成像角度，但TDICCD相机成像必须具备两个严格的成像条件：像移速度与行积分时间匹配，同时像移方向与TDICCD行积分方向一致，否则会导致成像模糊。假设经过积分时间Δt卫星位置、速度向量为P′和V′，计算t+Δt时刻瞬时轨道坐标系到地心直角坐标系的旋转矩阵R′obt-eth，用R′obt-eth和t时刻的Rrth-obj相乘得到R′。将M(t)、P(t+Δt)和R′代入共线方程可以求得(t+Δt)时刻的像面坐标(x′,y′)。

这时，“像移方向与TDICCD行积分方向一致，电荷转移周期与单级CCD积分时间Δt一致”的要求等价于x-x'=npix，y-y'=0(这里的像元数npix表示CCD尺寸，(x,y)为目标M在t时刻的像面坐标，(x′,y′)为目标M在(t+Δt)时刻的像面坐标，x和x′方向为行积分方向)。若x-x'≠npix，则积分时间Δt应修改为Δt′

图2为旋转角度k=0时的星下点轨迹和成像范围及对应的靶标模拟影像。可以看出，原本“正南正北”方向的输入靶标，在模拟影像上呈现一定角度的倾斜，成像范围的左右边界也与南北方向呈一定的角度，这个特点与我国多数卫星影像类似。

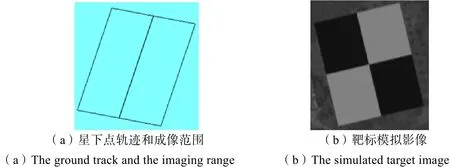
图2 k=0时的星下点轨迹、成像范围及对应的靶标模拟影像Fig.2 The ground track, the imaging range and the simulated target image when k=0

2 成像姿态计算方法

2.1 “南北方向”计算方法

通过绕u2向量轴旋转一个角度k仅仅可以实现影像行在地面的投影与纬线方向接近，相邻的影像行中心轨迹仍然是沿星下点方向的，这样不仅不能实现“南北方向”成像，还会导致TDICCD成像模糊。图3为k=13°时的星下点轨迹和成像范围及对应的靶标模拟影像，可以看出，左右两侧边界仍然与星下点轨迹近似平行，与南北方向呈一定角度。如果不结合滚动角运动，间隔时间Δt的列坐标差与行坐标差比值(y-y')/(x-x')达到0.25，靶标模拟影像出现严重模糊，不满足TDICCD相机的成像条件。

图3 k=13°时的星下点轨迹、成像范围及对应的靶标模拟影像Fig.3 The ground track, the imaging range and the simulated target image when k=13°

要想使该方向变为南北方向，必须通过横滚方向的姿态运动实现，因此需要确定一个滚动角速度ω˙或者经过一个行积分周期的变化量Δω。本文定义滚动的基准轴(即绕哪个向量轴旋转)为归一化速度向量uv。Δω的计算依据是实现t时刻和(t+Δt)间的列坐标之差为0，即y-y'=0。

式中f为相机焦距。

绕u2轴旋转角度k对应的旋转矩阵Rk通过四元数法计算，累积的滚动角ω对应的旋转矩阵Rω由uv和ω通过四元数法计算。

最终的旋转矩阵R为

图4为k=13°并在模拟计算时加入滚动角对应的Rω矩阵星下点轨迹、成像范围及对应的靶标模拟影像，可以看出，左右两侧区域边界已经接近南北方向，靶标模拟影像清晰，符合TDICCD相机的成像条件。

图4 k=13°，考虑滚动角速度，星下点轨迹、成像范围及对应的靶标模拟影像Fig.4 The ground track, the imaging range and the simulated target image when k=13° with corresponding ω˙

2.2 “摆扫”计算方法

这里的“摆扫”成像指的是将CCD列方向相比常规的CCD列方向旋转90°，通过绕卫星速度向量轴的姿态运动实现扫描成像，也就是 CCD列方向与卫星“前进方向”一致。这里的“前进方向”以卫星本体坐标系与瞬时轨道坐标系重合为前提，否则两者并不一致(如卫星绕卫星与目标连线向量旋转一个角度时)。对于TDICCD相机，需要横滚角和俯仰角同时变化才能满足TDICCD相机的严格成像条件。

在通过初始姿态计算实现“正对”目标成像的条件下，卫星绕u2向量轴旋转k角度，通过四元数法得到旋转矩阵Rk。假设卫星绕前进方向向量轴uv的旋转速度为ω˙，则相邻两行中心成像时刻间的旋转角度 Δω=ω˙×Δt，由uv和 Δω通过四元数法得到旋转矩阵Rω。假设P(t)与星下点连线向量为un，uv与un的叉积为up，则间隔Δt的俯仰角变化量Δφ计算方法为

同样由累加的俯仰角φ和向量up通过四元数法得到旋转矩阵Rφ。

总的旋转矩阵R计算方法为

图5为不同旋转角k同一轨道成像的星下点轨迹和地面范围，图6为不同k旋转角对应的模拟靶标影像。可以看出同一星下点轨迹下可以实现各种角度的成像，并且在48级积分条件下没有出现成像模糊。图6中k=0°时的模拟靶标影像，与图2（b）相比，成像角度旋转了90°。图6中k=13°时的模拟靶标影像，与图4（b）相比，成像角度也旋转了90°，但同样实现了“正南正北”成像。也就是说“摆扫”成像模拟方法适合任意k旋转角度，“正南正北”成像或“正东正西”成像只是众多角度的特例。

图5 同一轨道星下点轨迹不同旋转角度k及辅助俯仰姿态运动对应的成像范围Fig.5 Imaging ranges corresponding to different k-rotation angles and auxiliary pitching attitude motions under the same orbit

图6 旋转不同角度k的靶标影像（48级积分）Fig.6 Target images of different k with 48 levels integration

3 偏离星下点成像仿真

假设卫星飞行轨迹上离目标点最近的时刻为t0，对应卫星位置为P(t0)。则在t0时刻之前或之后间隔时间Toff对目标成像即前视或后视成像（Toff前视为负值，后视为正值），而t0时刻星下点与目标点存在一定距离时则为侧视成像。目标中心经纬度为（L,B）时，卫星星下点在同一纬度B对应的经度为Lnir，Lnir与L差异ΔL越大，侧摆角度越大。假设t0时刻的星下点向量为un0，t0时刻星下点与对P(t)连线向量为unp，un0与unp间的夹角即Toff时刻的前、后视角度。假设P(t0)与目标点连线向量为uM0，un0与uM0间的夹角即ΔL对应的侧摆角度。

图7为k=13°时不同视角的星下点轨迹、成像范围及对应的靶标影像。可以看出靶标图像变小，这是因为偏离星下点成像分辨率由于物距增大而变低，但地面范围同样接近“正南正北”效果。同时，靶标影像没有出现模糊。图8为“摆扫”成像条件下目标区域偏离星下点时不同旋转角度k的地面范围和对应的模拟靶标影像。靶标影像同样没有出现模糊，证明了姿态计算方法的通用性。虽然都能实现“正南正北”方向成像，常规推扫式成像的行积分时间还是取决于卫星沿轨道运动的固有速度，而“摆扫”式成像的行积分时间则主要取决于横滚方向摆动的速度，摆动速度越快，积分时间越短，单位时间成像范围越大。当然，这种优势也是以卫星的姿态控制能力为前提的，并且积分时间过短必然需要较高的积分级数才能保证理想的信噪比。

图7 不同视角的星下点轨迹、成像范围（k=13°）及靶标影像Fig.7 Ground tracks and imaging ranges with different angles （k=13°）and target images

图8 旋转不同角度k的成像范围和对应的模拟靶标影像Fig.8 Imaging ranges and target images of different k

4 结论

通过本文的姿态计算方法得到的地面范围和靶标成像结果可以看出，TDICCD相机沿非星下点方向成像无法通过单个姿态角的调整实现，需要通过滚动角或俯仰角的运动才能满足两个严格的成像条件。本文的基本思想是，间隔一个积分时间周期，仅改变旋转矩阵，同一地面点的投射像点在像面行列方向的坐标应满足行方向间隔一个像素，列方向坐标相同，这与TDICCD相机要求的两个严格成像条件相对应。将投射行、列坐标与理想坐标的差异转换为像空间的角度旋转量，根据像空间和物空间的对称关系，这个旋转量就是TDICCD相机对目标“严格”成像所需的旋转角度。试验证明，基于本文提出的旋转角度计算方法，可以实现各种不同角度的地面成像范围，在48级积分成像条件下，忽略姿态高频颤振等因素的条件下，靶标影像不会出现模糊，验证了仿真方法的正确性。