发掘直尺辅助教学功能举要

刘风云

摘   要：直尺是小学数学课堂中较为重要的教具和学具。在教学中，教师可充分挖掘直尺的辅助作用，帮助突破教学难点、常规问题创新思路、绘制多种图形、帮助建立模型思想、帮助形成书写技能等。在充分考虑学生的认知水平和活动经验的前提下，利用好身边常用的工具，提高学生学习数学的兴趣和应用意识。

关键词：小学数学;直尺;发掘功能;辅助教学

中图分类号：G623.5   文献标识码：A   文章编号：1009-010X（2021）19/22-0045-03

直尺是小学数学课堂中较为重要的教具和学具。在平时的学习中，直尺一般用来连线、画线段、画图形、画竖式中的等号线、测量长度等等，但其教学功能还可以进一步进行开发挖掘。

一、充分利用直尺长度，帮助突破教学难点

植树问题被安排在青岛版四年级上册智慧广场的内容中，其他版本教材有些则安排在五年级，可见这个问题是有一定难度的。

如题，“在20米的小路旁种树，每隔5米种一棵，两端都种，要种多少棵？”在非封闭的线上植树，当两端都种时，树的棵数=间隔数+1，为什么要加1呢？因为在0米处种了一棵树，所以要加1。“一条路的0米处”比较抽象，不好理解，这是本课的难点，怎样能让学生更直观形象地理解呢？在教学这个环节时，教师可以这样进行设计：

用20厘米长的直尺当小路，用铅笔或水彩笔当小树，每隔5厘米摆一棵。在直尺上，第一棵树正好对着0刻度，非常直观（见下图）。通过实际操作，学生明白了为什么间隔数加一等于棵数，因为在0米处要种一棵树，这个设计对于学生突破难点起到重要的作用。

复名数变单名数是小学数学教学中的一个难点。学生初次接触这部分内容是在一年级下册，这是学生名数互换建模的关键期，教材在名数互换方面主要涉及了两个领域：人民币的复名数变单名数和长度单位的复名数变单名数。以前教师经常借助人民币帮助建模，例如4元6角=46角。因为用人民币买东西贴近生活，是学生较为熟悉的题材内容，能有效帮助学生理解大单位和小单位之间的相加关系。随着互联网技术的发展，现在人们多用支付宝、微信等即时到付形式进行支付，用纸币的情境比过去少了很多，教学中已经不适合用这个情境进行建模。这时教师可以借助米尺帮助建模，使学生明确复名数中大单位和小单位之间的关系是相加关系。

仿用给同学量身高的形式，例如学生身高1米27厘米，先用米尺量出1米，做上标记，再用米尺量1米以上部分，通过这样的操作过程，直观形象地演示了1米27厘米其实是1米加27厘米，也就是127厘米。

低年级学生亲师性强，纷纷让教师给量身高，教师一边量身高，一边根据现实情境口头出题进行举一反三，1米36厘米等于多少厘米？1米45厘米等于多少厘米？同时逆向出题，139厘米等于多少米和多少厘米？124厘米等于多少米和多少厘米……课堂气氛活跃，学习效果非常好。

在《义务教育数学课程标准（2011版）》（以下简称《课标》）中明确指出，“重视学生已有的经验，使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。”可以看出来，课程标准倡导以“问题情境——建立模型——解释、应用与拓展”的数学建模模式。

教师创设学生熟悉的生活情境，精心设计和学生现实生活紧密联系的问题，能够激发学生建模的兴趣。

二、充分利用直尺刻度，常规问题创新思路

给三角形的一条底边做高是四年级下册第三单元内容，一般是用三角尺辅助，将三角尺的一条直角边和底边重合，过顶点做底边的垂线。其实利用一把直尺也能给底边做高，具体做法是：把直尺的0刻度线或者其他相对较长的刻度线和底边重合，过顶点画一条线段，这条线段就是底边的高，同时还能量出高的长度，一举两得，也就是说充分利用了直尺刻度线和直尺边所形成的直角，注意一定要使刻度线和底边充分重合。

三、充分利用直尺宽度，可以绘制多种图形

人们在利用直尺时，往往容易忽略利用直尺的宽度，只要动动脑筋，就有很多可挖掘之处。大多数直尺两面都有刻度，可以充分利用这些刻度和宽度。在直尺的两面分别选取相同长度的线段，如果相邻的顶点错开一下，就可以画出一个平行四边形;如果相邻的顶点相对，可以画出长方形;如果这两条线段和直尺的宽度相等，就可以画出正方形。在直尺的两面选取不同长度的线段，再封闭连接起来，就可以画出一个梯形。

依据是：一组对边平行且相等的四边形是平行四边形，四个角是直角的平行四边形是长方形，一组邻边相等的长方形是正方形，一组对边平行且另一组对边不平行的四边形是梯形。

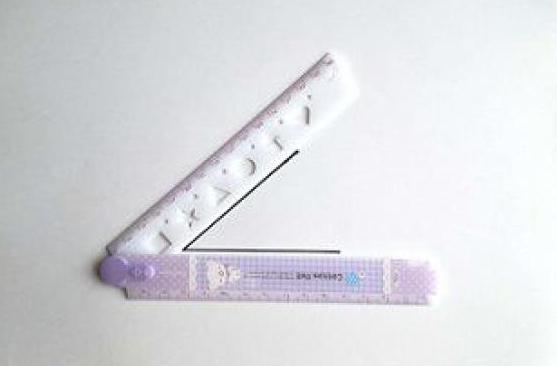
四、充分利用折叠尺的角度，轻松绘制角

折叠直尺是学生们的新宠，它能折叠，易存放，占用空间小，伸展空间大，殊不知它还可以开发画角的功能呢。做角、画角是二年级上册第三单元的内容，从一个顶点出发的两条射线形成一个角，学生们容易出现的问题有：两条射线不是从一个顶点出发;射线画不直等。利用折叠尺可以这样做：先确定一个顶点，从这个顶点出发利用折叠尺的角度画出一个角，轻松方便地完成。有的折叠尺顶端还有标有度数的半圆，甚至可以画出任意度数的角。

五、充分利用直尺尺身，帮助建立模型思想

（一）利用软直尺的尺身

有一种在封闭图形情况下的植树问题，例如：“为了保护一棵古树，园林处要为它做一个长20米的圆形防护栏。如果每隔2米打一个桩，一共需要打多少个桩？”或者有的题是设置在池塘、操场周围植树的情境，这种情况下间隔数和树的棵数之间是什么关系呢？怎样直观而形象地让学生明白其中的道理呢？

如果教师仅在黑板上画出圆形图或者方形图来帮助学生理解，纸上得来终觉浅，不如动手实际操作一下。把软塑料的直尺卷起来，当做“圆形防护栏”或者池塘，然后按照题意操作，得出结论，间隔数和树的棵数相等，学生们理解深刻，真是绝知此事要躬行。

《课标》中明确指出了建立模型思想的重要性和建立数学模型的途径方法。建立模型思想是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括：从现实生活或者具体情境中抽象出數学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想，提高他们学习数学的兴趣以及数学知识应用意识。

（二）利用硬直尺的尺身

冀教版小学数学二年级下册第八单元第二课，利用天平学习等量代换，先用跷跷板导入新课，然后用天平图推算。

天平是由支点、横梁、托盘、砝码组成的，教学时为了活跃气氛，培养学生的动手动脑能力和合作意识，可以进行小组合作自制小天平。这时直尺派上用场了，用直尺当天平的横梁，用一块小橡皮或者六棱铅笔的一个面作为支点，用大块橡皮和小块橡皮分别代表火龙果和桃子，根据题意2个火龙果的质量等于4个桃子的质量，推算出1个火龙果的质量等于2个桃子的质量。学生们兴趣盎然，积极行动，动脑思考，理解深刻。

六、充分利用直尺特征，帮助形成书写技能

在解答应用题时，有的教师要求学生在答题处先画上横线再解答，避免由于安排不合理而卷面凌乱，对于两步以下的应用题，这个办法不错。如果到了高年级，解题步骤多，并且有的用脱式计算，如果再提前画格子，不但耽误做题时间，而且卷面反倒更乱了。其实可以充分利用直尺，在低年级就养成用直尺标着写算式的习惯，久而久之，学生就具备了算式书写又直又整齐的技能，避免离了画格就写不了算式做不了应用题。

直尺的辅助教学功能不止这些，有一种直尺，尺身上有各种图形、数字、字母的缩小图例，还有的有数位顺序表，直尺还可以当裁纸刀，只要用心，会开发出很多功能。

《课标》第四部分“实施建议”中指出，“素材的选用应当充分考虑学生的认知水平和活动经验。这些素材应当在反映数学本质的前提下尽可能地贴近学生的现实，以利于他们经历从现实情境中抽象出数学知识与方法的过程”。小学生由于年龄小，活动空间有限，直尺是他们熟悉的学具，因此在教学中，我们要用心设计，充分挖掘直尺的辅助功能。