高考物理压轴题的破解方法

韦征

【摘 要】本文以高考物理压轴题为例，逐一分析破解方法：一是析情境，将复杂的实际问题转化为简单的物理模型;二是挖掘出隐含条件并将其显性化;三是寻找物体间或过程间的关联量，建立关联方程;四是构建待求量与已知线段或角度的几何空间，建立数学方程。

【关键词】高考物理压轴题 物理模型 隐含条件 关联方程数学方程

物理题难，物理压轴题更难，历年高考物理压轴题总让考生发怵、犯难。物理题尤其压轴题之所以难，一是题目本身复杂，二是解题者缺乏穿透力，看不透复杂性，理不清思路，导致学生束手无策。笔者根据多年教学经验，发现破解难题其实有法可依，有章可循。现笔者以高考物理压轴题为例，逐一分析破解方法。一是分析情境，将复杂的实际问题转化为简单的物理模型;二是挖掘出隐含条件，并将其显性化;三是寻找物体间或过程间的关联量，建立关联方程;四是构建待求量与已知量之间的线段或角度的几何空间关系，建立数学方程。下面选择几道典型的高考压轴题进行探究，供同行参考。

一、析情境

物理压轴题以力学综合题、电学综合题、电磁感应综合题居多，情境较为复杂，主要考查学生的理解能力、推理论证能力、模型建构能力、创新能力。要将复杂的实际情境转化为简单的物理情境，需要运用物理观念，即运用物理观念对复杂的实际问题进行分析、推理，进而进行逻辑判断。常运用的物理观念有物质观、运动观、相互作用观、能量观，运用这些物理观念将复杂的实际问题转化为物理模型。

比如，2015 年全国统一高考物理试卷（新课标Ⅲ）的第 25 题，以山体滑坡、泥石流的地质灾害为背景设置题目。在山坡 C 上有一质量为 m 的石块 B，它的上下表面与山坡 C 的坡面平行。石块 B 上有一含有大量泥土的石堆 A，A 和 B 均处于静止状态，如图 1 所示。假设在某一次大暴雨中，A 浸透雨水后总质量也变为 m（可视为质量不变的滑块），在极短时间内，A、B 间的动摩擦因数 μ1 减小为 ，B、C 间的动摩擦因数 μ2 减小为 0.5，A、B 开始运动，并以此时刻为计时起点。在第 2 s 末，B 的上表面突然变为光滑，μ2 保持不变。已知 A 开始运动时，A 离 B 下边缘的距离 l=27 m，C 足够长。设最大静摩擦力等于滑动摩擦力，山坡坡面的倾角为 。求：（1）在 0～2 s 时间内 A 和 B 的加速度;（2）A 在 B 上总的运动时间。

本题以地质灾害的山体滑坡或泥石流为背景，涉及多物体与多过程问题，考查匀变速直线运动规律和牛顿第二定律，考查学生建模能力和分析综合能力，考查的物理观念是运动观和相互作用观。题目中虽然已经把一些次要的影响因素过滤掉，留下本质性的影响因素，但其物理过程还是比较复杂。因此考生要分析题目所给的情境，把需要求解的运动问题简化为滑块 B 和物体 A 及物体 C 之间的运动关系。也就是说，运用运动和相互作用定律将山体滑坡或泥石流这个复杂的实际问题转化为“斜面上的板块问题”，建立“斜面上的板块”的物理模型。分析这个物理模型，进一步将“滑块 B 和物体 A”的运动关系转化为“追击模型”，然后运用匀变速直线运动规律和牛顿第二定律求解问题。

二、挖隐含

物理压轴题之所以难，有时是因为题设条件有隐含的条件，需要考生认真阅读、细细品味，从一些关键词中挖掘出隐含的信息，将隐含条件显性化。物理压轴题干的关键词往往是一些形容词，诸如最大、最小、最高、恰好、恰能等。若物体做直线运动达“最大速度”或“最小速度”，那么其隐含的条件是“物体所受合外力为 0”;若物体做曲线运动达到“最大速度”或“最小速度”，那么其隐含的条件是“物体所受外力在曲线切线方向上的合力为 0”;若“恰好”通过圆周轨道的最高点（或等效场的最高点），那么其隐含的条件是“对轨道的压力为 0”;若两物体“恰好分离”，那么其隐含的条件是“物体间的弹力为0，两物体的速度、加速度相同”。

比如，2018 年全国统一高考物理试卷（新课标Ⅲ）的第 25 题：“如图 2 所示，在竖直平面内，一半径为 R 的光滑圆弧轨道 ABC 和水平轨道 PA 在 A 点相切，BC 为圆弧轨道的直径，O 为圆心，OA 和 OB 之间的夹角为 α，。一质量为 m 的小球沿水平轨道向右运动，经 A 点沿圆弧轨道通过 C 点，落至水平轨道。在整个过程中，除受到重力及轨道作用力外，小球还一直受到一水平恒力的作用。已知小球在 C 点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为 0。重力加速度大小为 g。”在题干中“已知小球在 C 点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为 0”，隐含的条件是“在物理最高点 C，重力与水平恒力的合力为向心力，且小球过 C 点时的速度最小”。“光滑圆弧轨道 ABC”隐含的条件是“小球在圆弧轨道中运动时所受合力的方向指向圆心”。

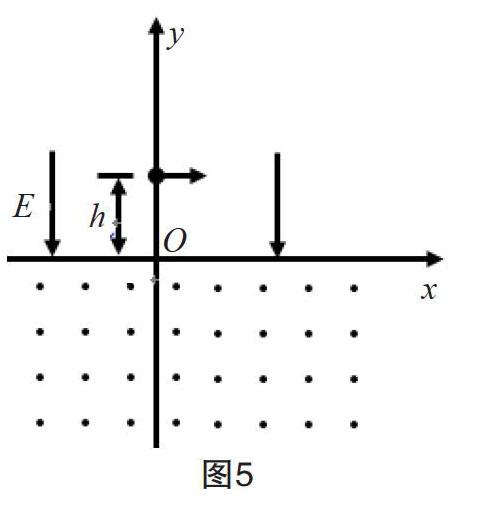
又比如，2020 年全国统一高考物理试卷（新课标Ⅰ）的第 25 題：“在一柱形区域内有匀强电场，柱的横截面是以 O 为圆心，半径为 R 的圆，AB 为圆的直径（如图 3 所示）。质量为 m，电荷量为 q（q>0）的带电粒子在纸面内自 A 点先后以不同的速度进入电场，速度方向与电场的方向垂直。已知刚进入电场时速度为零的粒子，自圆周上的 C点以速率 v0 穿出电场，AC 与 AB 的夹角 θ=60°。运动中粒子仅受电场力作用。为使粒子穿过电场后的动能增量最大，该粒子进入电场时的速度应为多大？”（部分）所求的“为使粒子穿过电场后的动能增量最大”中的“动能增量最大”隐含的条件是，粒子穿过电场的入射点 A 与出射点 D 间的电势差为最大，出射点所在等势面必与柱形区域的边界相切，如图 3 所示，作与 BC 平行的直线与圆相切于 D 点（出射点），与 AC 的延长线交于 P 点，则自 D 点从圆周上穿出的粒子的动能增量最大。

三、寻关联

物理压轴题很多涉及多个物体或多个过程，在审题时要有时空观念，要有意识地分析多个物体之间的联系、分析多个过程之间的联系，并寻找物体间或过程间的关联量。在分析题意中，寻找到哪些是与力、时间、位移、速度有关联的，并把这种关联与物理定律、规律联系起来，进而建立与关联物理量有关的方程—— 关联方程。这是分析的基本点，也是关键点，因此建立“关联方程”往往是求解压轴题的突破点。

比如，2020 年全国统一高考物理试卷（新课标Ⅱ）的第 25 题：“如图 4，一竖直圆管质量为 M，下端距水平地面的高度为 H，顶端塞有一质量为 m 的小球。圆管由静止自由下落，与地面发生多次弹性碰撞，且每次碰撞时间均极短;在运动过程中，管始终保持竖直。已知 M=4 m，球和管之间的滑动摩擦力大小为 4 mg，g 为重力加速度的大小，不计空气阻力。（1）求管第一次与地面碰撞后的瞬间，管和球各自的加速度大小;（2）管第一次落地弹起后，在上升过程中球沒有从管中滑出，求管上升的最大高度;（3）管第二次落地弹起的上升过程中，球仍没有从管中滑出，求圆管长度应满足的条件。”

本题以竖直圆管与地面的碰撞为背景，涉及多物体与多过程，考查匀变速直线运动规律、牛顿第二定律、动能定理等知识，考查学生推理能力和分析综合能力，考查的物理观念有运动观、相互作用观、能量观;求解第一问时必须审视“管和球”之间的相关量：摩擦力;求解第二问时必须审视“管和球”的时间关系、速度关系和位移关系;要求圆管长度应满足的条件，必须审视“管和球”的相对位移。

四、构空间

有些物理题之所以难，其实难点不在物理知识，而在于数学知识。在解物理题中，由纯粹的几何空间关系建立的方程称之为数学方程。如在几何光学光路问题中，寻找入射角、反射角或折射角与有关线段的函数关系;再如带电粒子在匀强磁场中运动问题中，寻找轨迹半径与有关线段的函数关系，这些函数即数学方程。要建立数学方程，必须构建待求量与已知线段或角度的几何空间关系，这往往是求解物理压轴题的突破点之一。

本题以带电粒子在电场和磁场中的运动为背景，是单体多过程问题，考查了运动观、相互作用观，考查了平抛运动、圆周运动、电场力、洛伦兹力等知识，考查了考生借助数学知识分析物理综合问题的能力。

本题的求解要关注在电场中类平抛运动和在磁场中圆周运动这两个过程间的关联：一是类平抛运动的末速度是圆周运动的初速度，二是平抛运动的水平位移是圆周运动的弦长。第 2 和第 3 两问均涉及“圆周运动半径与已知线段”的关系，要找到它们的关系必须构建“圆周运动半径与已知线段”三角形空间，如图 6 所示（阴影部分）。

以下以 2018 年全国统一高考物理试卷（新课标Ⅰ）的第 25 题为例，完整地说明如何依章循法破解难题。

这是这些年来高考物理试题中难的典例，许多考生在考场中无法解出（2）（3）问;不少老师也曾尝试求解，有的教师花费近 40 分钟，均无功而返。据甘肃、重庆两省市考试院公布的统计数据，两省市该题的平均分分别为 1.82 和 2.016，难度系数分别为 0.09 和 1.01，因此很多教师都迫切地想知道究竟有何妙招能快速破解这道难题。

我们分析发现，本题以带电粒子在重力场和复合场的运动为背景，涉及两个物体、两过程。两个物体：带电小球 M、N;两过程：一是在重力场中的运动，二是在复合场（重力场与电场）中的运动。考查平抛运动规律、匀变速直线运动规律、牛顿运动规律、运动的合成与分解;考查建模能力和分析综合能力，考查的物理观念有运动观、相互作用观、能量观。本题的妙解方法如下：

这道压轴题解法的精妙之处在于两点：一是审题时，注重文字描述中的补充说明，挖掘其隐含的条件。如：“N 离开电场时的速度方向竖直向下”“M 在电场中做直线运动”“刚离开电场时的动能为 N 刚离开电场时动能的 1.5 倍”等，可参见解答中对这些条件的利用。二是寻找关联。本题注意寻找 M、N 两球的关联，“由 A 点以相同的初速度做平抛运动”“在水平方向有相同大小的加速度、在竖直方向也有相同的加速度”;同时注意寻找两阶段运动的关联，即“小球在电场区域内外两阶段运动的时间相等”。

物理压轴题的破解，可依据“析情境、挖隐含、寻关联、构空间”的章法，层层分析、抽丝剥茧。因此，在平时指导学生进行审题时，教师要重视括号内的文字以及题干部分的最后说明，这些条件往往是解题的突破点。此外，物理计算题所列方程通常有三类，第一类是根据物理规律或公式建立的方程，这类方程称之为“基本方程”。第二类方程则是根据物体之间的关联或过程之间的关联建立的方程，这类方程称之为“关联方程”。第三类则由纯粹的空间关系建立的方程，这类方程称之为“数学方程”。在计算题的解答过程中学生易建立“基本方程”，但“关联方程”和“数学方程”难以建立起来，因此，要在计算题上有突破，教师在平时的习题训练中应加强这方面的指导。

（责编 李 唐）