玩转数“9” 开放思维 勾勒全貌
陈元云 邢成云
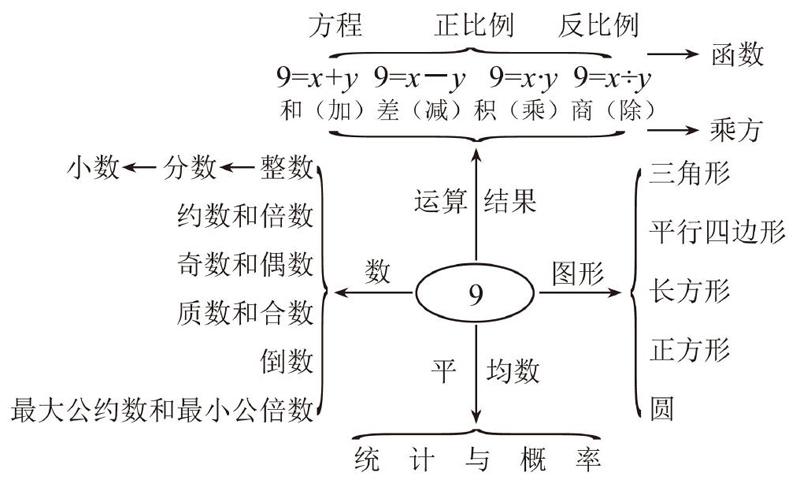
【摘 要】 在邢成云老师提出的“整体化教学”[1]主题思想的引领下,基于学生小学数学已有的“零散”的学习经验,在义务教育数学课程标准(2011版)理念的指导下,从“9”出发,提出问题,开放思维,引导学生提炼升华,总结规律,锻炼思维逻辑,初步见识初中数学的大概内容,为学生“顺利”进入中学的数学课堂,驾好引桥,扫清障碍,让学生在“先见林,再见木”的序化逻辑中播下初中数学学习的种子.
【关键词】 整体思维;发散思维;开学第一课
学生由小学进入初中,不仅仅是身份的变化,而且在学习上也会发生很大的变化,尤其是数学的学习,孩子们初中三年数学能力的养成与数学教师平时每一节课的引导息息相关.如何让学生具有整体思维的逻辑,让数学学习来得自然些、親切些、有趣些,就需要在课堂教学中,适切、时切地给学生搭建思维发展逻辑进阶的平台.基于此,笔者对学生进入初中后的数学“开学第一课”进行了如下设计.
1 以“9”作基,唤醒对“数”的认识
课堂开始,笔者便在黑板上醒目地写下了数字“9”,提出问题:今天我们就利用小学学到的数学知识,共同探讨一下对“9”的认识.听到问题,学生展现出了“懵懵”的状态,但在思考之后,思维开始活跃起来.
生1:9是由9个1组成的,9是整数.
生2:9是最大的一位数.
生3:9是奇数,也是合数.
生4:9的因数有1,3,9.
生5:9是18的一个因数,9也是27的一个因数,9还是36的一个因数……
生6:9的倍数有无数个,比如9,18,27,36,….9的最小整数倍是9,没有最大的倍数.
生7:9的约数有1,3,9.
生8:9是9和18的最大公约数,9也是9和27的最大公约数……
生9:9是3和9的最小公倍数,9也是1和9的最小公倍数.
生10:9的倒数是1/9.
此时,学生的思维出现了短暂的“停滞”,我顺势引导:同学们的回答很好,由这些对“9”的认识,你想到了我们小学学过的哪些数学知识?
生11:小学学过的数按照不同标准可以分为奇数和偶数,质数和合数,还有约数和倍数,最大公约数和最小公倍数,还有倒数等.
师:大家说得很好,揭秘了“9”作为数出现时,可能会产生的“意义”.
设计意图 先引导学生从数的角度认识“9”,完成了对小学学到的数的整体认知,这些按照不同标准产生的不同类型的数,也正是初中数学学习中经常用到的.借助这个环节,打开学生思维,为后面的环节做好铺垫.
2 解剖数“9”,再识小学的四种运算
评价完学生回答以后,笔者提出新的问题:我们小学只学习了“数”吗?你还能想到其他知识吗?
生12:我们还学过了数的运算.
师:那这个数字“9”是不是可以看成一个运算结果呢?请大家继续探讨对“9”的认识.
生13:9可以看成5与4的和,6与3的和,7与2的和,8与1的和.
学生一边回答,教师一边板书:9=( )+( ).
追问:9只能看成两个整数的和吗?有没有其他情况?
生14:9也可以看成三个整数的和.
师:还有其他可能吗?我们学过的数有哪些?学生沉默几秒钟,再一次出现了“跃跃欲试”的情境.
生15:9还可以看成8.1与0.9的和,或者看成7.1与1.9的和,这样的话,9=( )+( )中的两个加数会有无数个答案.
生16:9还可以看成81/4与3/4的和,当然这两个加数也有无数个答案.
师:同学们对小学学过的数学知识的调度很灵活,请大家继续思考,9只能看成两个数的和吗?
生17:当然可以看成两个数的差,比如10与1的差,12与3的差,……
教师板书:9=( )-( ).
生18:9也可以看成10.1与0.1的差,103/4与13/4的差,……(此时教室里响起了掌声)
生19:9可以看成两个数的积.
教师板书:9=( )×( ).
生20:9=(9)×(1),9=(0.3)×(30),9=(10)×(9/10),……,这两个因数也有无数个答案.
追问:两个因数中有没有特殊情况?
生21:两个因数相等,此时9=3×3=32.
师:对于32是我们进入初中以后要研究的一种新运算“乘方”.
追问:同学们还有想说的吗?
生22:9还可以看成两个数的商.
教师板书:9=( )÷( ).
生23:9=(9)÷(1),9=(3)÷(1/3),9=(10)÷(10/9),……,这里的被除数和除数也会产生无数个答案.
师:同学们太厉害了,由“9”作为运算结果又联系到了我们小学学过的所有数的运算,再次见证了了数的“成长”历程(整数—小数—分数),并进一步认识到数及其运算构成了小学数学的核心内容.
设计意图 借助当“9”作为运算的结果时,对小学所学习的四种运算进行了复习,这样不仅引发了学生的深度思考,而且发散了学生思维,尤其是当“9”作为和、差、积、商时,对应的加数,被减数、减数,因数,被除数、除数会产生无数个对应的答案,学生不仅仅再次感悟了数的成长过程,而且体验了数学的开放性.
3 以“9”导疑,加深对正比例、反比例、方程的认识,渗透函数概念
师:刚才我们把9看成了一个运算的结果(和、差、积、商),对于这四种运算,我们能从另外一个角度去认识吗?比如:9=(x)+(y)中,这里的x、y替代了上面具体的数,这是小学已经初步认识的什么知识?
生:字母表示数
师:对,这样一来就构成了一个关系式,这个关系式中隐藏着什么?
生24:x与y的和是9,9比x大y,或者9比y大x,也可以是x比9小y,y比9小x.
师:那在减法运算,9=(m)-(n)中呢?
生25:m比n大9,或n比m小9,与加法中蕴含的等量关系相同,它们都表示了两个数之间的数量关系.
师:那在乘法运算中,又隐藏着什么等量关系呢?比如:9=(a)×(b)中?
生26:a的b倍等于9,b的a倍等于9,9是a的b倍,9是b的a倍.
师:那在除法运算中呢?比如:9=(c)÷(d)中?
生27:与乘法运算中隐藏的等量关系相同吧.
师:也就是在加减法运算中,表示了两个量的和差数量关系;而在乘除法运算中,表示了两个量的倍分数量关系.请大家继续思考:看到9=(a)×(b)时,你又想到了我们小学学到的什么数学知识?
生28:此时的a和b成反比例关系.
追问:那你看到9=(c)÷(d),又想到了?
生29:此时的c和d成正比例关系.
师:在9=(x)+(y),9=(m)-(n),9=(a)×(b),9=(c)÷(d)(借板书指出即可)中,还有什么共同点?
生30:它们都是等式.
生31:等式右边的两个数字都不是唯一的,有无数个(对应)值.
生32:它们都含有两个未知数.
师:同学们的发现都很好,这些式子(板书的四个等式)不仅仅是等式,还含有未知数,这些未知数还具有可变性,可见它们有着更加丰富的内涵,这些式子从小学的角度来看应该是什么?
生33:方程.
师:是的,它们可以看成方程,只不过是含有两个未知数的方程,有待我们的进一步研究.另外,我们进入初中以后这些式子还可以看成是初中代数内容中另一类很重要的新知识——函数.(借此板书:函数)由此我们也可以看出,同样一个式子竟然有两种不同的认识,这在告诉我们知识具有相承性,它们不是彼此剥离的,而是认识的不断发展,所以说初中数学无非就是小学数学的再次生长.
师(总结):以上我们又从数量关系的角度对“9”进行了探索,认识到加减乘除四则运算中除了蕴有外在形式的方程外,还隐藏着函数.这样,我们就初步见识到了初中数学“数与代数”领域的概貌.
设计意图 先引导学生对这四种基本运算9=(x)+(y),9=(m)-(n),9=(a)×(b),9=(c)÷(d)所表达出来的式子进行分析,揭示出其中所蕴含的等量关系,加减表达了和差关系,乘除表达了倍分关系,这也是小学与初中最为常用的两个等量关系;再借助9=(a)×(b),9=(c)÷(d)两个式子,领悟得出小学所学到的比例知识,这其实就是初中要研究的正比例函数和反比例函数的知识,而9=(x)+(y),9=(m)-(n)则是初中研究的一次函数,由此导出初中要研究的知识点——函数,最后再借助这些式子的共同点(等式),导出了方程的知识,这样也完成了对小学数学“数与代数”内容的整体架构,又顺利的把初中数学函数知识“牵”出来,在学生心中埋下了函数知识的“种子”.
4 以“9”布疑,形成“图形”的知识体系
借助对“9”的认识形成了小学学过的数的知识架构之后,笔者再次提出问题:同学们在小学除了学过的数及其运算以外,还有其他知识吗?学生思维再一次出现了暂时的停滞,停顿了1分钟左右,学生思维再度出现“高潮”.
生34:除了有关数的内容以外,我们还学过图形的有关知识.
追问:那我们对“9”是否还有其他的认识?
生35:9可以看成边长为3的正方形面积.
生36:那9当然也可以看成长方形的面积了,这个长方形的长和宽分别是9和1.
生37:长和宽不一定是整数吧,因为长方形面积等于长×宽,我们刚才分析了9=( )×( )中的因数有无数个,所以如果长方形的面积等于9,则该长方形的长和宽是不确定的,有无数个答案.
生38:9还可以看成平行四边形的面积啊,因为平行四边形的面积是底×高,所以底和高也是有无数个答案.
生39:9还可以看成一个三角形的面积或者梯形的面积,分析方法与上面相同.
生40:那9也可以看成一个圆的面积啊,也就是πr2=9.
生41:这个有点难,我们还不会确定圆的半径.
师:是的,我们暂时还不能确定这个圆的半径,但初中待学习的一種新运算可以解决这个问题,同学们是不是有所期待!
追问:刚才我们把“9”看成了图形的面积,除此之外,我们还学过图形的什么?
生42:周长,那“9”也可能是我们上面分析的图形的周长.
追问:如果把“9”看做图形的周长,那分析的方法与“9”做为面积时,分析的方法一样吗?
生43:当然相同了,就是把面积公式改成周长公式就行了.
师:很好.以上,我们借助数字“9”,完成了对小学所学到的图形知识的总结,这些也将是我们进入初中以后要重点研究的图形.与小学一样,进入初中,我们也是要重点研究三角形、平行四边形、长方形、正方形、圆这些基本图形的,只是研究的角度不同了,同学们能说一下,我们小学研究这些图形,主要从什么角度研究的吗?
生44:如何计算这些图形的周长、面积,也就是从“数量”的角度.
师:回答的很好,进入初中以后,我们将在以上定量研究的基础上,转向对图形的定性研究.
设计意图 本环节继续对“9”探究,得出9可能是一个图形的面积或者周长,因为由以上几个环节的铺垫,学生得出结论自然是水到渠成的事.该环节也是既帮助学生完成了小学所学到的所有的基本图形(平面图形)的知识架构,又为学生进入初中以后要研究的几何图形提前布下了局.
5 以“9”引疑,拎出统计与概率
师:以上我们从不同角度对“9”进行了“解密”,大家能否借助我们上面分析问题的经验,继续思考呢?
生45:那还可以怎么认识“9”呢?得想想我们小学还学了什么?
生46(忽然站起来):9可能是几个数字的平均数,比如:9是1和17的平均数,也是2和16的平均数,总之,9可以是很多个这样的两个数字的平均数,也可以是三个数字的平均数…….
追问:这些内容又属于数学中的哪一部分呢?
生47:统计.
师:对,除统计以外,在小学我们还学过了可能性的知识,知道事件发生的可能性有大小,这些也将是我们进入初中要继续研究的“统计概率”的知识范畴.
设计意图 本环节实际上是学生类比上面几个环节自主提出问题的,这样小学数学的知识架构基本形成了,顺乎其然,初中数学的基本架构也就诞生了.
6 总结提炼,升华收获
师生再次回顾小学学过的数学知识结构图,同时“反射”出初中数学的知识架构.
师:至此我们把小学学过的主要内容梳理了一遍,看同学们的表现是很不错的,初中的学习无非就是以上知识的再次生长,期待同学们初中学习的精彩!至此我们立足小学的学习,初步勾勒出了初中数学学习的概貌,初步感触到了已有知识的生长性,在此期待同学们善用类比、善用联想、用开放的思维去迎接初中数学学习的挑战.
设计意图 课堂小结再次把课堂上得出的零散收获进行汇总,帮助学生形成策略性知识.这样就为学生顺利进入初中数学课堂做好了铺垫,本节课做为学段起始课的立意——开思维、见全貌、提兴趣的“先行组织者”作用就有了.
7 反思评价
7.1 借用数字“9”质疑开塞,巧妙唤醒小学知识
本节课是给新初一学生上的开学第一课,对于本学段起始课,少有老师有意规划,绝大部分老师是忽略的,几乎都是直赴新授课的教学.上课结束时,几个“活跃”的孩子惊讶的说:数学原来还可以这么“玩”啊,一个小小的数字竟然能把所有的小学知识都“揪”出来,而且还这么轻松,挺有意思.本节课中学生的思考与回答应该是最好的诠释——玩转数字“9”,提炼升华,把小学学到的零散的知识凝成知识架构,为初中的数学课堂描绘出了蓝图,见到了“森林”,吊起了学生对数学学习跃跃欲试的胃口.
7.2 借力“类比”思想,为初中数学学习埋下伏笔
本节课借助对数字“9”的认识,引导学生体会数学应用的广泛性以及数学的价值[2],实际是在渗透给学生要学会用数学的眼光看待“世界”,用数学的思维表达世界的意识.同时借助小学的知识架构,反射初中数学的学习内容,这实际都是大“类比”思想的应用,同时也是在帮助学生促成正迁移,在课堂上可见学生的这种迁移在悄悄发生,学生竟然可以类比前三个环节的设计,自己探讨第四个环节,长此以往,学生的类比迁移能力会不断得到提升.
7.3 设计适切的教学任务,引发学生的深度思考
学习任务是学生参与课堂学习的重要载体和平台,教学任务的设计直接影响到学生的课堂效率,同时也关乎学生数学能力的提高.因此,在课堂教学中,学习任務的确定至关重要.本节课中,我没有让学生去做多少具体题目,而是给学生提供可引发“深度思考”的素材,让学生在开而有度的问题驱动下,既活跃了思维、回顾了知识,又提高了综合调度知能储备的能力.
7.4 整体立意,大处着眼,以点带面见全貌
整节课以“学段起始课”为出发点,借助邢成云老师提出的“整体化教学”[1],从大处着眼,以培养学生的兴趣、打开学生思维为宗旨,引导学生见到了初中数学的“全面貌”,形成了“课程”体系,这样学生可以明明白白的进入初中的数学课堂,为学生顺利适应初中数学课堂做好了引领与铺垫.
参考文献
[1]邢成云.整体化教学:课堂直指学生思维发展[N].中国教育报,2019-12-11(10).
[2]中华人民共和国教育部.义务教育数学课程标准(2011版)[S].北京:北京师范大学出版社.2012.

