一种缘自“审美抽象”的数学慢教育研究

朱桂凤

【摘 要】 以“主视图、左视图、俯视图”教学为载体，展现一种缘自“审美抽象”的数学慢教学气象.审美抽象包括“展开与收起”命令、“行动与规则”条件、“有序与无序”表达，并以此回答研究对象为什么、是什么和怎么样的哲学命题.突出“慢道”与“慢理”，及其背后“向阳而生”的新时代课堂特征，落实“育人>教书”的行为责任目标.

【关键词】 审美抽象;数学慢教育;哲学思考;概念产生式

《普通高中数学课程标准（2017年版2020年修订）》开宗明义，数学抽象是指通过对数量关系和空间形式的抽象，得到数学研究对象的素养.审美抽象是数学抽象的终极目标，是通过知觉的途径、以感性直观的方式使对象中的普遍意义呈现出来，在数学慢教育论域中表现为直观基础上的概念和概念关系的建立，突出无序中的规律性、复杂中的简单性、孤立中的统一性、平凡中的审美心理倾向.

在慢教育课堂，审美抽象不是单纯的感性抽象，而是感性基础上的理性抽象，是学生“能学好”不可绕过的途径，包括“展开→收起”命令、“行动→规则”条件、“有序→无序”表达，以此回答审美抽象对象为什么、是什么和怎么样的哲学命题，落实数学慢课堂上好课、上好学、育好人的时代课程目标.本文以“主视图、左视图、俯视图”教学为行为载体，展现一种缘自“审美抽象”的数学慢课堂的教学气象，突出“向阳而生”的新时代课堂特征.

1 “展开→收起”命令，回答审美抽象对象“为什么的问题”

“展开”与“收起”是EN5软件在“授课状态”下系统自带的功能，是将“立体图形”转化为“平面图形”、“平面图形”转化为“立体图形”的命令性程序（展开命令、收起命令），这种符合学生知觉认知特点的知识加工过程，能够让学生直观感知规则图形的对称性、统一性和非平衡性（三维对称、二维对称、一维对称），提高了学生获得研究对象的能力.换句话说，展开、收起的过程就是研究对象得以审美抽象、理解输出的过程，促进审美需要的内在心理冲动、认知冲突与平衡.

譬如，在图1（1）中，通过“观察学习”，在动态“图形转换”的过程中，学生能直观读懂几何体圆柱的展开图就是一个长方形和两个圆;在图1（2）中，几何体圆锥的展开图是一个扇形和一个圆;在图1（3）中，几何体四棱柱的展开图是3对规格不同的长方形，呈现对称常规，有助于后续“三视图”的本质揭示.其中，展开图的作用不止于直观“转换”的懂，更在于有序显化立体图形对称的非平衡性.具体地说，几何体圆柱、四棱柱是三维对称（上下对称、左右对称、前后对称）、圆锥是两维对称（左右对称、前后对称）.这些看似不起眼的概念和概念关系要素，没有动态生成过程，学生对“展开”与“折叠”的认识是肤浅的、或者说是不完备的、甚至是反直觉的，这就是研究对象获得的首要条件和理解的“重头戏”.尤其是，初中阶段学生的“抽象思维水平”显著低于“形象思维水平”的条件下，使用“展开→收起”命令，为不同学生的数学理解提供了无限的可能性.用马克思的话说就是“完整的表现蒸发为抽象的规定.”意味着舍弃对象的全部丰富的具体的细节、特征和属性，这当然符合审美的目的性，这就是慢教学、慢课堂慢的“道”与“理”.

当然，慢教育的过程不止于“漫溯长篙”，更在于研究对象的获得细节.让学生在“展开与折叠”的体验中，获得互逆的、补偿的抽象感，才是慢的关键.因为，学生习得了将“知识”转化为“能力”的能力（逆向思考、可逆补偿）.正如专家们呼吁，没有经历“研究对象”获得过程的课堂是“去教育”的教学，是违背教育规律的，是要叫停的.为此，笔者进一步发问“为什么要从三个方向看同一个物体？”（见图1）言外之意，为什么不从四个方向、五个方向、六个方向看同一个物体呢？经历这样的哲学思考，学生能懂得物理空间规则几何体，只要三视图就能知道整个几何体的概貌.也就是说，当前我们研究的对象是一般的规则的几何体，这就自然引进课题（主视图、左视图、俯视图）.同时，必须强调我们生活的物理空间存在大量的一维对称的规则物体，像人类和其它动物，基本上是左右对称的生命体，要认识其概貌必须“五视图”.另外，还存在一些不规则的几何体（斜棱锥等），如果要认识其概貌，则需要“六视图”.这样的审美抽象是慢的可逆、慢的补偿、慢的体验，学生在不知觉中解除了心理认知冲突，理解教材编者为什么要研究“三视图”，哲学地回答了“为什么研究”的问题.然而在现实课堂教学中，很少有老师关心这样的问题，往往采取忽略的态度，直奔课题、“打转”小学阶段的思维.其实，这才是最有价值问题，是学生最想知道的问题，是老师需要下功夫研究的问题.

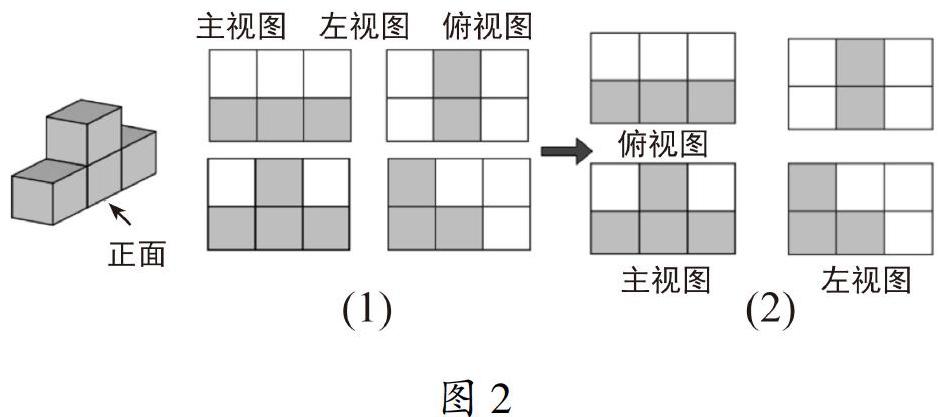
是的，审美抽象作为慢教育的顶层设计，属于现象学的一个组块，有助于在平凡中抽象出审美倾向、在孤立中抽象出统一性.正如《论一种缘自認知心理学及教育学研究的数学认知过程》[1]一文指出，“数学现象-心象-抽象-操作”过程，是一种可应用于中学数学教学的“数学认知过程”.这种过程缘自认知心理学与教育研究，基本上体现反映论观点，强调“数学现象”的概念和观点，对数学教育教学有重要意义.为此，笔者设计了一种可逆补偿思维事项（见图2），旨在让学生通过“猜测、预见、拖图”的方式，在“概念辨别”和“同化衔接”层面，将小学阶段的“从正面看、从左面看、从上面看”自然过渡到中学阶段“主视图、左视图、俯视图”.这样，直观地“调用”经验，既促进了学生认识新概念的审美需求，又接好了认知“地气”.也就是说，“展开与收起”直观地回答了为什么这样，而不是那样的哲学命题.

2 “行动→规则”条件，回答审美抽象对象“是什么的问题”

“行动→规则”（简称C→A规则）属于计算机科学领域的名词，被称为产生式（production）.“行动（condition）”是保存在短时记忆中的信息，“规则（action）”是人经过学习，其头脑中存储了一系列以“如果/那么”的形式表示的规则（这种规则被称为产生式），该规则不止于外显的反应，还包括内在的心理活动或运算.譬如，《义务教育数学课程标准（2011年版）》描述“两条直线平行的基本事实：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.”其中，“如果同位角相等，那么这两条直线平行”就是规则或称产生式.而“同位角的概念、表示相等的抽象符号“=”、表示平行的抽象符号“∥”、过直线外一点有且只有一条直线与已知直线平行的基本事实等”都是“行动到规则”的操作条件.这种条件性的“行动”到“规则”的目标过程就是感性抽象理性化的一种显性表现，是审美抽象的内在表达机制.譬如，在图1（3）将四棱柱直观展开的过程中，就为后续规范画出“三视图”奠定了理性审美的基础.其中，展开图中的三类规格不同的长方形就是三个视图的“样子”，只不过放置方位不同，名称有所变换，但概念的本质不变.这就哲学地回答了“是什么”的问题，是“如果…，那么…”的思维结果.这就是审美抽象的一般形式，强调慢在直观、慢在知觉概括.

当然，抽象的产物应该是概念、判断和推理，但是这种理解主要是对逻辑抽象而言的.在慢教育教学论范畴，审美抽象则是经历知觉概括，显化概念对象（三视图）普遍意义的心理倾向和认知产生式，带有积极的认知心理学意义.因此，“行动→规则”审美抽象过程至少涵盖三个方面的思考：

第一，“做中学”，让学生在审美抽象中形成直观的“知觉辨别”.知觉辨别就是在一个或更多的物理或感觉维度上直观察觉出刺激差异的性能.譬如，在图3（2）中，学生能在“画图”中，指出从正面看、从左面看和从上面看，看到的图形“同”与“不同”，并说出同的共性、不同的差异性，这就是知觉辨别的常见思维方式.显然，知觉辨别是一类物体的空间观念，是准确辨别事物的“是”与“非”的条件.同时知觉辨别往往是由知觉概括的完备性决定的，现实生活中，这样的例子俯拾皆是.譬如，在“摸几何体”活动中，学生能准确从装有圆柱、圆锥、球和长方体、正方体的不透明袋中摸出圆锥，就是知觉辨别能力较好的表现.其中，“摸”是一种行动（感性抽象）、“摸出”是一种规则（审美抽象）.这样在慢思考中画出、在慢体验中摸出，在一定层面回答了“是什么的问题”.正如美国著名科学家、人工智能之父西蒙（Simon）指出，利用某种辨别网络（discrimination net）建立索引，从而使得在复杂情境中的线索能够被再认出来.

第二，“例中学”，让学生在审美抽象中建立“概念表象”（一类事物的心理映像）.例中学就是通过具体的例子来学习.当前，中学生学习的配套教材基本上都是一种例中学，例题、举例说明、反例等都是例中学的“关键词”.当然，例中学为概念表象建立了“个性”，“类”例中学则为概念表象建立共性提供了审美抽象的条件.在图3中，让学生在“画出”的体验中，将从正面看到的图形上升为主视图、将从左面看的图形上升为左视图、将从上面看到的图形上升为俯视图（概念表象），并用“下定义”的方式呈现出来，即“我们把…，叫做…”（规则、产生式系统），这就是慢概念，这就是抽象审美的必然结果.其中，画出圆柱、圆锥、四棱柱的三个视图就是“类”例中学的常見方式.正如“TEC教学”指出的那样，把“返璞归真教育、美育教育、数学发现法教育、数学家人品教育、数学史志教育”[2]等序列变量整合成三个变量因素加以研究（思想、情感、合作），能够促进“例中学”的育人质量.其中，返璞归真是一种认知审美、发现法是一种行动规则，美育教育与人品教育、史志教育是一种审美抽象.这种TEC教学方式是“慢学”的心理状态和“慢说”的行动方式，能让学生自然学、喜欢学，并产生“能学好”的无限可能性.

第三，“用中学”，让学生在审美抽象中形成“规则、程序及其概念产生式系统”.用中学就是让学生在应用概念中学习概念、在使用概念中深化理解概念，提高概念直观懂的水平.譬如，用1张a×a型纸片、2张a×b型纸片和1张b×b型纸片拼正方形，在整体与局部思想的参与下，通过“面积法”这一心理运算活动，可获得完全平方公式a2+2ab+b2=（a+b）2.这个过程就是一种审美抽象，是行动到规则的行为方式，很好地回答了完全平方公式是什么的问题，是从哪里来、要到哪里去的问题.当然，这样的审美抽象过程也是“用中学”的具体表现，属于使用概念、应用概念的常见思维方式.尤其在初中阶段，学生的“直观知觉能力>抽象认知能力”的条件下，用中学显得尤为必要和至关重要.学以致用、用以致学、学用结合都是行动到规则的有效载体，能提高知识实践价值和证实、证伪价值.

其实，一直以来，课程与教学的理论追求与现实实践都始终把“证实-求是”[3]作为指导思想，这是一种不健全的认识信念.只有注入“证伪”因素，形成“证伪→证实→求是”的教学产生式系统，方能提高“学”的质量和“学好”的能力以及行动到规则的审美力.也就是说，求是与去伪的融合是慢课堂审美的教学格局.譬如，在“三视图”概念表象建立的基础上，笔者设置了一个“反知觉问题”（见图4）.旨在让学生通过用概念，产生认知冲突，实现证伪与求是融合的目标，提高概念表象的区分度.具体来说，在图4中，“主图”没有给出正面，如何确认画出三个视图呢？这样旨在提供证伪条件;如果添加“正面”，三个视图又是如何变化的？旨在证实和求是，有利于促进审美抽象，提高慢课堂、慢教育的育人水平.这就是说，教师要清楚每一个问题设置的目的，行动到规则成就了学生什么，知识技能、思想方法、社会智慧等都要科学预见，方能上好课、育好人、教好学.

3 “有序→无序”表达，回答审美抽象对象“怎么样的问题”

在哲学审美与哲学表达范畴，“有序”是一种闭合抽象，是对“道生万物”内在思考秩序的表达，有约束地展现审美抽象揭示的规律性.譬如，研究“走进图形世界”这一单元内容时，首先研究常见几何体的抽象特征，其次研究图形的运动及其展开与折叠（互逆思维），最后研究三视图相关知识体系.这种基于知觉抽象基础上的概念和概念关系的建立、空间图形与平面图形的转换以及视图与投影，都是有序认识事物的一般规律，带有程序性知识加工的一般意义，是“类概念”建立绕不开的途径.有如黑格尔的观点，“类的存在”是逻辑抽象的结果，而在“此杂多中寻求统一的要求”，就是抽象的意志和能力.笔者把这里的“类的存在”理解为结构、单元、组块以及当前提倡的任务性大单元教学体系、甚至是大概念思想的引进，这有助于学生建立认知理解的内在秩序，最终是将结构性知识转化为认知结构，从而促进审美表达.同时，这里的“此杂多中寻求统一”就是在无序的事物中发掘出极度的规律性和统一性.譬如，用小长方形纸片拼大长方形，在面积思想和局部整体思想的参与下，发现“一个多项式如果能分解因式，用面积相应的小长方形纸片就能拼成大长方形;否则，反之.”这就是在无序中抽象出规律性的经典例子.

当然，在慢教学审美范畴，有序是常规，无序是开放，“有序到无序”的表达是一种直观上的半开放抽象，能让学生获得不同角度看问题的能力.这能为学生走向社会工作好、学习好、生活好奠定积极的心理基础，包括开放的思维、开阔的视野和包容不同的能力.这些看似无用的东西恰恰是最有用的东西（无用之用方为大用），恰恰是课堂教学应该充分关注的东西.就这一意义来说，慢教育慢在无序、慢在生长、慢在美我所美、慢在统一.为此，在有序到无序表达中，如何通过审美抽象心理过程的介入，回答好概念对象“怎么样的问题”，是个实践变量，是对“远近高低各不同”的审美表达.

第一，“有序”合审美抽象约束的目的，有助于规范学生的画图行为，回答了怎样“画好概念”的问题.譬如，在图5中笔者设置了组合几何体，在不同规格表格的约束下，力图让学生规范画出三个视图.这里的“有序”至少表现在三个方面：一方面，规定了正面，为学生确立三视图画法提供了精确的方位;另一方面，给出了符合画图条件的表格，引领学生规范地画出与约束地表达;再一方面，直观呈现学生的思维共识，有助于概念关系的抽象与审美表达.图5是笔者对课本客观问题的改造与提高，力图让学生适应“方格”到“非完全方格”的心理变化过程，提高审美抽象的心理水平.在“画出”的过程中，慢在顺应、慢在重组、慢在客观经验的确立以及有序思考的数学品格的涵养.美国《品格教育宣言》中指出，品格教育并不只是一堂课或一个课程，一个迅速实行的计划或贴在墙上的口号[4];而是创新、严谨、坚强意志、勤奋、坚持不懈、理性、独立思考、勇于质疑、实事求是、化繁为简、数学兴趣的审美叠加，是回答在“画出”过程中经历了怎样的思维挫折和思考意志，获得了怎样画好的方法算理和真知灼见（长对正、宽相等、高平齐）.

第二，“无序”合审美抽象的半开放原则，有助于学生习得一般化能力，回答了怎样规范呈现概念的一般方式.譬如，在图6中，笔者设置了无序问题组块，力图让学生在寻求画好、表达好的过程中建立一般意义的概念关系，从而科学地回答怎样画好概念体系的一般方法.从慢的认知需要看，隐去视图表格，有助于学生深化理解“长对正、宽相等、高平齐”的画法原则;从慢的审美需要看，“无中生有”文化，有助于催生规范，激发学生探问三个视图怎样放置的问题？从而确立科学规范的方法体系，即一般情况下，我们将左视图放在主视图的右边、俯视图放在主视图的下方.这样，为后续能读懂桥梁设计、房屋建筑、机械制造、城市規划等图纸铺设审美基础;从自我实现需要看，三个几何体的组织成分是简单到复杂、视图的方位由特殊（规定）到一般（无规定）、三视图的结构由显性到隐性，这为审美抽象带来了弹性思考空间，有助于学生各美其美和兴趣满满.这些“需要”是学生能到达那里的支持条件，是一种慢的智慧，慢在无序、慢在“一般画”.

另外，在“育人>教书”的目标过程中，慢教育预留了哲学、心理学、美学的思考阵地，“留白”是哲学，“审美抽象”是心理过程，而在无序中抽象出有序的规律是一种美，合美的无目的性.心理学家菲希宾（Efrain Fishbein）感叹道：“似乎数学家和心理学家坐在一起后并没有什么共同话题.”实际上，并非如此.因为历史上数学家勒贝格、庞加莱、阿达玛、波利亚都对数学创造发明的心理过程作出精辟的分析[5].因此，慢课堂是向阳而生的，补给了人成长过程中必须的哲学、心理学和美学的营养元素，促进人的充分成长，这就是“慢道”与“慢理”，这就是审美抽象的顶层设计.

文献参考

[1]王明杨，徐沥泉，徐利治.论一种缘自认知心理学及教育学研究的数学认知过程[J].数学教育学报，2013，22（01）：33-36.

[2]吴勤文，杨世明.对“TEC教学”基础的反思[J].数学教育学报，2007，16（01）：21-24.

[3]喻平.教学的应然追求：求是与去伪的融合[J].教育学报，2012，8（04）：28-33.

[4]祖丹，孔凡哲.数学必备品格的组成要素分析——基于数学家的视角[J].天津师范大学学报（基础教育版），2020（2）：59-65.

[5]谢明初，朱新明.认知心理学下的数学教育[J].数学教育学报，2007，16（01）：12-16.