交错管束间湿空气-水蒸发冷却特性模拟

麻宏强， 刘叶敏， 梁诺， 贾继伟， 罗新梅， 厚彩琴，曲德虎， 王刚， 张娜

(1.华东交通大学 土木建筑学院，江西,南昌 330013；2.兰州理工大学 土木工程学院,甘肃,兰州 730050)

换热管束作为换热设备基本部件，目前被广泛应用于工业生产换热设备，如石油化工、电厂、冶金厂和中央空调等领域.换热管束的换热方式主要有交错管束间对流换热和交错管束间蒸发冷却换热.前者属于单相流换热，而后者是多相流换热.交错管束间蒸发冷却换热过程属于多相流换热，其传热传质过程机理比较复杂.由于不同研究间存在分歧，可能导致交错管束蒸发冷却设计计算不合理，造成换热工艺难以满足设计要求等严重后果.因此，有必要对交错管束间蒸发冷却传热传质特性进一步研究.

目前，对交错管束间单相流传热特性的研究比较多，主要集中在不同运行参数及管束结构参数对传热特性的影响.GU等[1]对航空用交错管束传热特性进行了研究，LI等[2]比较了普通波纹翅片管束和三角翼平板翅片管管束间传热性能.对交错管束间湿空气-水蒸发冷却的研究，主要集中在喷淋水-管壁间对流换热系数和喷淋水-湿空气间传质系数两个关键参数上.但由于对交错管束间蒸发冷却传热传质过程机理的认识不足，不同研究存在分歧.NIITSU等[3]和ZHU等[4]认为传热系数是喷淋水流量的单值函数；同时，ZHENG等[5]和HEYNS等[6]通过研究发现，传热系数不仅与喷淋水流量和喷淋水温度有关，而且与空气流量成正比.对于传质性能的研究，FACO等[7]和HASAN等[8-9]的研究表明，传质系数仅随空气流量增大而增大；而HEYNS等[6]通过研究发现，传质系数是空气流量和喷淋水流量的函数，并随空气流量和喷淋水流量增大而增大；同时HANNO等[10]发现传质系数不仅与空气流量和喷淋水流量有关，而且随喷淋水温度升高而增大.

同时，也有许多学者通过数值模拟方法对交错管束间蒸发冷却传热传质进行了研究，但这些计算模型并未充分考虑喷淋水滴在管壁形成液膜的过程、喷淋水滴在湿空气中的传热传质，以及水滴和液膜蒸发产生的水蒸气在湿空气中的扩散过程，这对计算结果造成了较大的误差.比如：GAN等[11-12]、HASAN等[13]采用DPM模型对交错管束间湿空气-水蒸发冷却过程中的传热性能进行了研究.该研究仅考虑了交错管束与湿空气间的显热换热，并未考虑喷淋水蒸发及蒸发引起的潜热换热.XIE等[14]基于DPM模型建立了交错管束间喷淋水-湿空气间传热传质模型，对光管、椭圆管和纵肋管束间湿空气-水蒸发冷却传热传质特性进行了模拟研究.但是该计算模型未考虑喷淋水膜在管束壁面的流动过程，这可能会对计算结果造成误差.因此，不少文献对喷淋水流动特性进行了模拟分析.如ZHAO等[15]、DING等[16]、KARMAKAR等[17]和XIE等[18]对管束壁面水膜流动特性进行了研究，但这些研究未涉及传热传质.综上所述，针对交错管束间湿空气-水蒸发冷却传热传质特性，目前已做了大量工作，但这些模型并不能完整描述交错管束间蒸发冷却传热传质过程.

文中针对上述问题，综合考虑喷淋水滴在管壁形成液膜的过程、喷淋水滴在湿空气中的传热传质过程，以及水滴和液膜蒸发产生的水蒸气在湿空气中的扩散过程.采用基于DPM与WFM模型耦合的欧拉-拉格朗日方法，建立交错管束间湿空气-水蒸发冷却传热传质特性分析模型，并通过实验数据对其进行了验证；利用FLUENT软件模拟研究了空气流量、干湿球温度、喷淋水流量及喷淋水温度对交错管束间蒸发冷却传热传质特性的影响.

1 数理模型建立

1.1 物理模型简化

文中依据文献[12]中交错管束结构，对长(L)宽(B)高(H)分别为1.2 m、0.6 m和1.55 m交错排列交错管束进行研究；其管排数为24排，列数为10列，共228根管束；管束外径为10 mm，横向管中心间距为60 mm，纵向管中心为20 mm.由于交错管束结构长度大于等于宽度的两倍L≥2B，因此，对三维结构进行简化，取垂直于盘管方向二维平面结构进行分析[12-13].同时，又因为交错管束关于中心线对称，所以只对一半进行建模，如图1所示.

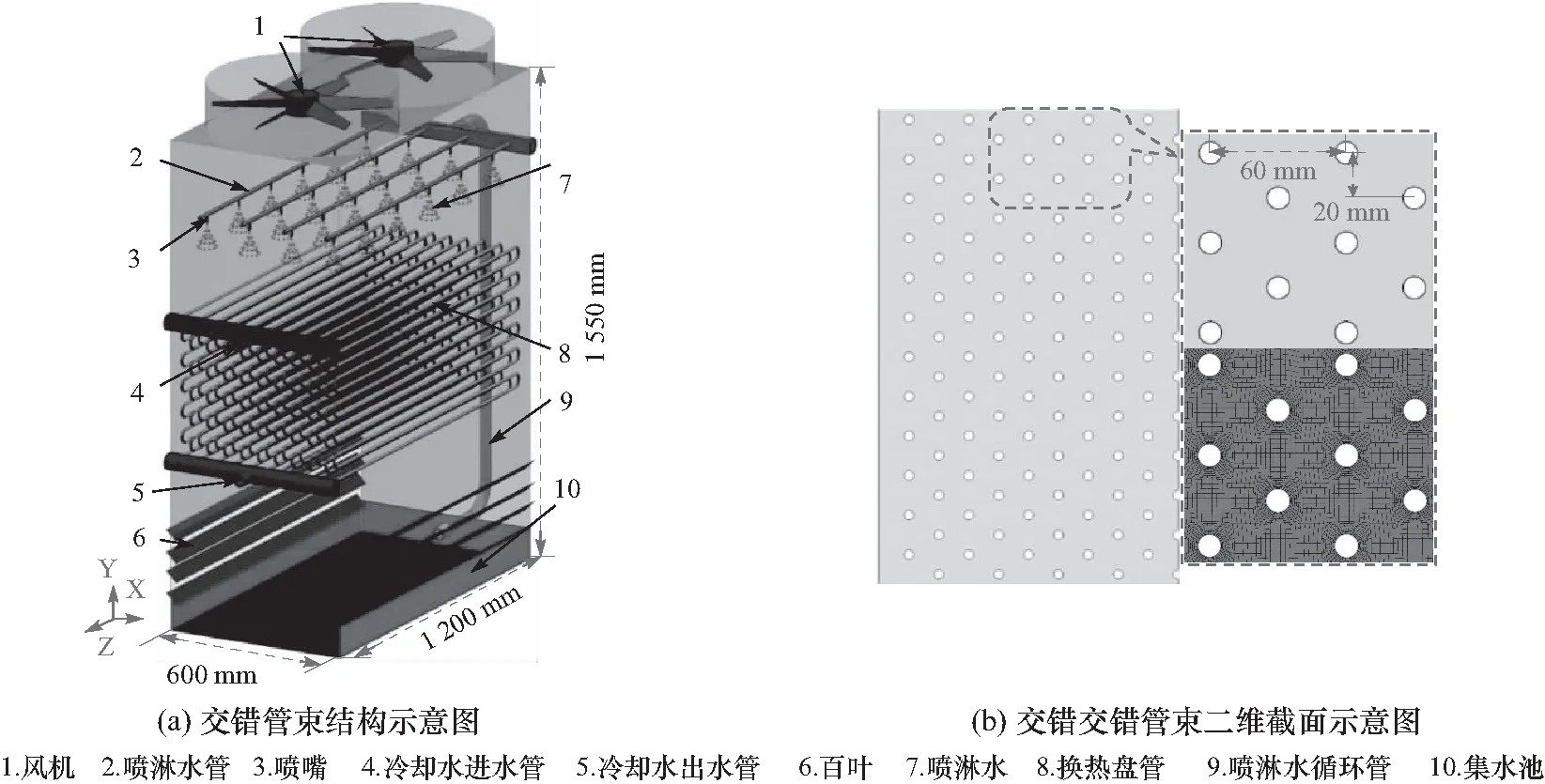
图1 交错管束几何模型Fig.1 The geometric model of staggered tube bundle

1.2 数学描述

文中采用基于DPM与WFM模型耦合的欧拉-拉格朗日方法，综合考虑喷淋水在管壁形成水膜的过程、喷淋水滴在空气中的传热传质，以及水滴和水膜蒸发产生的水蒸气在空气中的扩散过程，建立交错管束间湿空气-水蒸发冷却过程分析模型，对其传热传质特性进行模拟分析.交错管束间湿空气-水蒸发冷却传热传质，涉及喷淋水滴-湿空气之间传热传质，喷淋水膜-湿空气之间传热传质，以及喷淋水滴和水膜蒸发后产生的水蒸气，在湿空气中的传质等过程.由于传热传质过程非常复杂，为了便于计算，需对其做相应假设：

① 管表面的润湿性沿管轴线保持不变，不考虑液膜沿轴向运动.

② 将水滴视为球形液滴，且由于喷淋水体积流量小于流场总体积的12%，因此采用DPM模型对水滴进行分析.

③ 空气和水滴在流场中是同时存在，其均为不可压缩流体.

1.2.1喷淋水滴-湿空气传热传质过程数学描述

交错管束间的湿空气-水蒸发冷却过程可描述为喷淋水从交错管束顶部喷嘴喷出后，形成大量的水滴，这些水滴在重力、阻力和浮力的共同作用下，进入交错管束间隙，与湿空气进行传热传质.依据牛顿第二定律，交错管束间的单个喷淋水滴运动方程可表达为

(1)

式中：mp为单个喷淋水滴质量；up为喷淋水滴矢量速度；u为湿空气矢量速度；ρ为湿空气密度；ρp为喷淋水密度；g为重力加速度；τp为水滴松弛时间.喷淋水滴松弛时间τp可表达为[19]

(2)

式中：μ为湿空气动力黏度,N·s/m2；dp为喷淋水滴直径；Cd为喷淋水滴阻力系数；Red为喷淋水滴相对湿空气的相对雷诺数.其中，水滴相对湿空气的相对雷诺数Red可表达为[19]

(3)

水滴在下落过程中，由于水滴表面张力的作用，使得水滴表面积尽可能达到最小，因此将交错管束间的喷淋水滴视为球体，根据文献[20]，式(2)中喷淋水滴阻力系数Cd可表达为

(4)

式中：a1，a2和a3为常数，MORSI和ALEXANDER[20]给出了不同Red范围的适用值.

喷淋水滴在交错管束间运动过程中，喷淋水滴-湿空气间还存在热质交换过程.喷淋水滴-湿空气间通过显热和潜热交换，实现喷淋水滴的蒸发，产生的水蒸气通过扩散进入湿空气.喷淋水滴向湿空气的蒸发速率与喷淋水滴-湿空气界面表面传质系数、喷淋水滴表面水蒸气浓度以及主流湿空气中水蒸气浓度有关.因此，单个喷淋水滴蒸发速率可表示为

Ni,p=kc(Ci,s-Ci,∞)

(5)

式中：Ni,p为喷淋水滴表面单位面积上摩尔蒸发速率,kmol/m2·s；kc为喷淋水滴-湿空气界面水蒸气传质系数,m/s；Ci,s为喷淋水滴表面水蒸气摩尔浓度,kmol/m3；Ci,∞为主流湿空气中水蒸气摩尔浓度,kmol/m3. 式(5)中喷淋水滴表面水蒸气摩尔浓度Ci,s为水滴温度Tp对应饱和水蒸气压Psat下水蒸气的摩尔浓度，其可表示为

(6)

式中：R为通用气体常数，取8.314 J/(mol·K).

式(5)中主流湿空气中水蒸气摩尔浓度Ci,∞可表示为

(7)

式中：Xi为湿空气中水蒸气的摩尔百分数；Pv为水蒸气分压力,Pa；T∞为湿空气温度,K.

根据文献[21],式(5)中的喷淋水滴-湿空气界面水蒸气传质系数kc表示为

(8)

式中：Di,m为水蒸气在湿空气中的扩散系数,m2/s；Sc为Schmidt数，Sc=μ/ρDi,m，μ为湿空气动力黏度,Pa·s；dp为喷淋水滴的直径,m；Red为水滴相对湿空气的相对雷诺数，由式(3)计算得出.

在喷淋水滴-湿空气蒸发冷却传质过程中，喷淋水滴质量将发生变化，根据质量守恒原理，某t时刻喷淋水滴的质量mp(t)等于t+Δt时刻喷淋水滴蒸发质量与蒸发时间间隔Δt内喷淋水滴蒸发质量之和.因此，单个喷淋水滴质量方程可表示为

mp(t)=mp(t+Δt)+Ni,pApMw,iΔt

(9)

式中：Mw,i为喷淋水分子量,kg/kmol；mp为单个喷淋水滴质量,kg；Ap为单个喷淋水滴表面积,m2；Δt为喷淋水滴蒸发时间,s.

喷淋水滴在下落过程中与湿空气进行显热和潜热换热后，喷淋水滴温度将发生变化，依据能量守恒原理，单位时间内喷淋水滴热量变化等于喷淋水滴-湿空气间显热换热量与喷淋水滴-湿空气间因蒸发而产生的潜热换热量之差.湿空气向喷淋水滴传热方向为正，则单个喷淋水滴的能量守恒可表示为

(10)

式中：cpp为喷淋水比热容,J/(kg·K)；Tp为喷淋水滴温度,K；hp为喷淋水滴-湿空气间对流换热系数,W/m2·K；T∞为湿空气温度,K；dmp/dt为喷淋水滴蒸发率,kg/s；hfg为喷淋水汽化潜热,J/kg.

1.2.2水膜形成及水膜传热传质过程数学描述

喷淋水滴在交错管束间向下运动过程中，部分水滴将会接近盘管壁面，并与盘管壁面发生碰撞.水滴撞击盘管壁面后，将会发生4种不同的状态：①喷淋水滴直接黏附在壁面；②喷淋水滴在壁面扩散伸展；③喷淋水滴直接被反弹出去；④喷淋水滴破裂，一部分留在壁面，一部分飞溅出去.喷淋水滴与管束壁面碰撞后发生的不同状态取决于喷淋水滴所具有的冲击能量和管束壁面温度，喷淋水滴碰撞壁面的结果可根据图2确定.

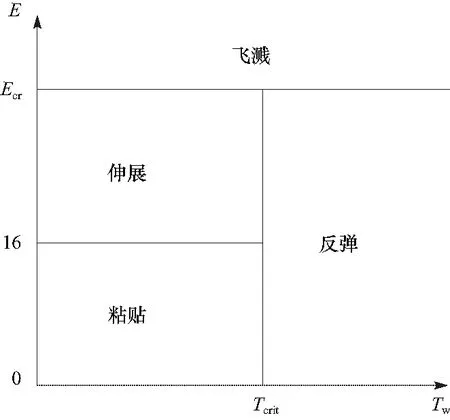
图2 喷淋水滴与壁面碰撞关系Fig.2 The relationship between spray water drop and wall collision

也就是说，管束壁面温度Tw小于临界温度Tcrit时，喷淋水滴撞击后可能会出现黏附、扩散或飞溅现象；管束壁面温度Tw大于临界温度Tcrit时，撞击后的喷淋水滴可能会反弹或飞溅；当喷淋水滴撞击前的冲击能量E小于临界冲击能量Ecr时，撞击后的喷淋水滴可能会出现黏附、扩散或者反弹现象；当喷淋水滴撞击前的冲击能量E大于临界冲击能量Ecr时，撞击后的喷淋水滴会出现飞溅现象.

依据上述分析，要确定喷淋水滴碰撞管束壁面后的状态，需要确定喷淋水滴碰撞壁面的冲击能量以及临界壁面温度.根据文献[22-24]喷淋水滴碰撞壁面的冲击能量E被定义为

(11)

式中：upn为喷淋水滴垂直于壁面速度分量,m/s；ρp为喷淋水密度,kg/m3；dp为喷淋水滴直径,m；σ为喷淋水表面张力,N/m；hδ为管束表面微元体内水膜厚度,m；δbl为壁面水膜边界层厚度,m.

临界壁面温度可表示为[22]

(12)

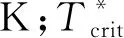
喷淋水滴与管束壁面在碰撞作用下，喷淋水滴将在管束表面形成喷淋水膜，并沿管束周向开始运动.喷淋水膜在自身重力、壁面对喷淋水膜剪切力和湿空气对喷淋水膜剪切力的综合作用下，沿管束周向开始运动.依据牛顿第二定律，喷淋水膜的运动方程可表示为

(13)

式中：ufilm为喷淋水膜速度矢量,m/s；hδ为微元体内喷淋水膜高度,m；Gfilm为喷淋水膜所受重力,N/m2；τw为壁面对喷淋水膜剪切力,N/m2；τg为湿空气对喷淋水膜的剪切力,N/m2.其中喷淋水膜重力可表示为

Gfilm=ρphδ(g-αw)

(14)

式中：ρp为喷淋水的密度,kg/m3；g为重力加速度,m/s2.

壁面对喷淋水膜的剪切力可表示为

(15)

喷淋水膜在管束壁面流动过程中，不仅受到力的作用，而且喷淋水膜与湿空气间还存在质量交换过程.在喷淋水膜-湿空气交界面，喷淋水膜蒸发速率主要由喷淋水膜表面和主流湿空气的水蒸气浓度差及喷淋水-湿空气交界面水蒸气传质系数决定.管束表面微元体内喷淋水膜蒸发速率可表示为

Ni,film=kfilm(Ci,s-Ci,∞)

(16)

式中：Ni,film为微元体内喷淋水膜-湿空气交界面单位面积上，喷淋水膜摩尔蒸发流率,kmol/(m2·s)；Ci,s和Ci,∞分别为喷淋水膜表面水蒸气摩尔浓度和湿空气中水蒸气摩尔浓度,kmol/m3；kfilm为喷淋水膜-湿空气交界面水蒸气传质系数,m/s.

喷淋水膜与湿空气在蒸发传质过程中，管束壁面喷淋水膜的质量将发生变化，依据质量守恒，某t时刻喷淋水膜的质量mp,film(t)等于t+Δt时刻喷淋水膜蒸质量与蒸发时间间隔Δt内喷淋水膜蒸发质量之和.因此，单个喷淋水滴质量方程可表示为

mp,film(t)=mp,film(t+Δt)+Ni,filmAp,filmMw,iΔt

(17)

式中：Mw,i为喷淋水分子量,kg/kmol；Δt为喷淋水蒸发时间,s；Ni,film为微元体内喷淋水膜-湿空气交界面单位面积上，喷淋水膜摩尔蒸发流率,kmol/(m2·s)；Ap,film管束表面微元体内水膜表面面积,m2.

一方面喷淋水膜与湿空气间存在潜热交换，另一方面喷淋水膜与管束表面及湿空气间还存在显热换热过程.在这些换热过程的综合作用下，喷淋水膜自身温度将发生变化.依据能量守恒原理，喷淋水膜的能量变化量等于喷淋水膜-管束壁面间换热量、喷淋水膜-湿空气间对流换热量与喷淋水膜-湿空气间汽化潜热量之差，微元体内液膜温度变化可表示为

Ni.filmAp,filmMw,ihfg

(18)

式中：mp,film为管束表面微元体内喷淋水膜质量,kg/s；cpp为喷淋水比热容,J/(kg·K)；Tp,film为喷淋水膜的温度,K；Qp,cond为管束壁面-喷淋水膜间导热量,W；Qp,conv为喷淋水膜-湿空气间对流换热量,W；hfg为喷淋水汽化潜热,J/kg.

管束壁面为热流边界时，式(18)中管束壁面与喷淋水膜之间的导热量Qp,cond可表示为

(19)

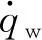
式(18)中喷淋水膜-湿空气间的对流换热量Qp,conv将通过下式计算：

Qp,conv=Ap,filmhfilm(T∞-Ts)

(20)

式中：hfilm为喷淋水膜-湿空气间对流换热系数,W/(K·m2)；Ts为微元体内湿空气侧液膜表面温度温度,K.由于喷淋水膜具有一定的厚度，水膜内部温度与水膜表面温度不同，因此用水膜中间温度表示液膜温度.图3为喷淋水膜双线性温度分布，Tw为管束表面温度,K；Tp,film为微元体内喷淋水膜的温度,K.

将式(19)和(20)代入式(18)，管束壁面微元体内喷淋水膜的温度变化可表示为

Ts)-Ni,filmAp,filmMw,ihfg

(21)

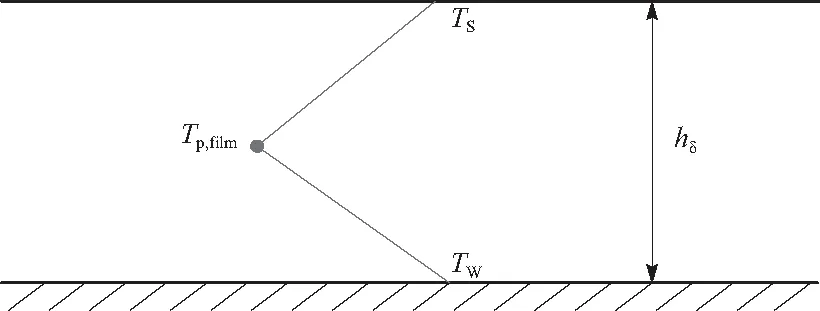
图3 喷淋水膜双线性温度分布的假设Fig.3 Assumption of bilinear temperature distribution of spray water film

1.2.3湿空气传热传质过程数学描述

湿空气在交错管束间向上流动过程中，不仅与管束间喷淋水滴通过蒸发冷却进行热质交换，同时与管束壁面喷淋水膜也进行热质交换.依据质量守恒原理，交错管束间微元体内湿空气质量变化量等于微元体内湿空气的净流入量与微元体内水滴和管束壁面水膜蒸发进入湿空气的水蒸气量之和.其可表示为

(22)

式中：ux,uy分别为x和y方向湿空气的速度,m/s；Sp,Sfilm分别为喷淋水滴和喷淋水膜蒸发进入湿空气的水蒸气质量流率,kg/(m3·s).

湿空气在交错管束间流动过程中，不仅满足质量守恒，也需要满足力平衡方程.同时，湿空气在交错管束间流动为湿空气重力及喷淋水滴和水膜对湿空气作用力互相作用的结果.根据牛顿第二定律，在重力、表面压力、黏性力、喷淋水阻力的合力下，微元体内湿空气力平衡关系(动量方程)可表示为

(23)

式中：p为静压,Pa；μ为湿空气动力黏度,Pa·s；gy为湿空气在y方向的重力,m/s2；Fx,Fy为喷淋水滴对湿空气的作用力；μt为湍流动力黏度,Pa·s.式(23)中湍流动力黏度μt表示为

μt=ρCμk2/ε

(24)

式中：Cμ为常数，取0.09；k和ε分别为湿空气湍动能和湍流耗散率.根据上述分析，要求解力平衡方程，需要建立湿空气的湍动能和湍流耗散率方程.文中采用标准k-ε湍流模型，对湍流动能k及耗散率ε进行描述及求解，其可表示为

(25)

(26)

式中：Gk为由湿空气速度梯度产生的湍流动能；C1ε,C2ε为常数,分别取1.44和1.92；σk和σε分别为k和ε的湍流普朗特数，分别取1.0和1.3[25].

式(25)(26)中湿空气的湍流动能Gk表示为

(27)

湿空气在交错管束间流动传热传质过程中，也需满足能量守恒，即：微元体内流体的总能量变化量等于由于热对流流体通过界面净携入微元体内的能量、由于导热在界面处净导入微元体内的能量、湍流引入的能量与微元体内水滴和管束壁面液膜蒸发进入湿空气的潜热之和，其表示为

(28)

式中：keff为湿空气有效导热率,W/m·K；Ji,x,Ji,y分别为x和y方向水蒸气的扩散通量,kg/(m2·s)；SQ,p,SQ,film分别为水滴和水膜蒸发的水蒸气进入空气的能量,kW/m3.

交错管束间隙喷淋水滴和水膜蒸发产生的水蒸气，进入湿空气后，在湿空气中进行扩散，改变空间域湿空气的相对湿度，从而影响湿空气与喷淋水滴/水膜间的传质过程.湿空气中水蒸气的传质过程可表示为

(29)

式中：Yi为湿空气中水蒸气质量分数；Si为水蒸发速率,kg/(m3·s).

1.3 边界条件

对于交错管束间湿空气-水蒸发冷却传热传质特性数学模型，主要包括主微分方程和边界条件.根据质量守恒、力平衡以及能量守恒原理，确定了交错管束间湿空气-水蒸发冷却传热传质特性分析主微分方程，要使其有唯一解，需附加边界条件.因此，本节主要对交错管束间湿空气-水蒸发冷却特性分析边界条件进行分析.

喷淋水通过交错管束上方的喷嘴，在较高压条件下以水滴形式喷向交错管束间隙.喷淋水滴进入交错管束间隙后，与管束壁面和湿空气进行换热.在实际工程中，喷嘴喷出水滴的速度、温度以及流量通常为已知量；同时，喷嘴的孔径给定，喷嘴喷出的水滴直径也将已知.因此，在图1所示喷嘴位置，喷淋水滴状态可表示为

(30)

式中：up,in为喷嘴出口喷淋水滴速度,m/s；Tp,in为喷嘴出口喷淋水的温度,K；dp,in为喷嘴出口喷淋水滴的直径,m.

同时，湿空气通过底部入口，进入交错管束间与喷淋水滴/水膜进行热质交换.在湿空气进口处空气速度，温度、压力以及湿空气中水蒸气的含量(相对湿度)为已知量.因此，在湿空气入口处，湿空气状态可表示为

(31)

式中：uair,in为湿空气进口速度,m/s，不同工况取值不同；ρin为进口湿空气密度,kg/m3；Ta,in为湿空气进口温度，不同的工况取值不同；RH0为湿空气进口空气的相对湿度，不同的工况取值不同.

交错管束间喷淋水-湿空气传热传质流场中，喷淋水滴撞击管束壁面后形成水膜，因此，将管束壁面设置为“壁膜”边界.当喷淋水滴撞击空气进口和空气出口位置时，喷淋水滴将逃出交错管束间喷淋水-湿空气传热传质流场，喷淋水滴的控制方程停止计算，因此，将空气进口和空气出口设置为“逃逸”边界.

2 网格无关性及模型验证

2.1 网格无关性

网格的数量和质量对仿真精度和时间有着重要的影响.为了生成最合适的网格并捕捉精确的传热传质过程，在计算域中采用了结构化网格.靠近管壁区域进行了边界层划分，产生了比其他区域更密集网格节点.本节将在空气流量为0.8 kg/(m2·s)，温度为20.7 ℃时验证网格数量对计算结果影响，分别选取网格数量为16 000、57 000、138 000和261 000四套网格，如图4所示.比较了底层、中间层和顶层管束壁面温度变化，模拟结果如图5所示.当网格数量从16 000增加到261 000时，管束壁面温度显著降低.网格数量达到138 000时，底层、中间层和顶层管束壁面温度没有明显变化，证明网格数量为138 000的网格足够精细，能够满足仿真精度要求.

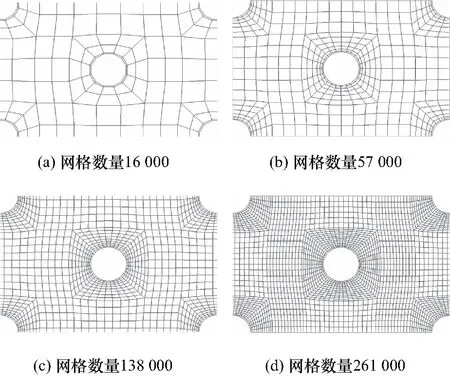
图4 交错管束局部网格分布Fig.4 Local grid distribution of staggered tube bundles

图5 不同密度网格管束壁面温度变化Fig.5 Temperature change of tube bundle wall with different mesh number

2.2 模型验证

本节对比文献[12]实验结果与模拟结果，验证模型准确性.图6是管束壁面温度预测值与实验值对比结果.其主要对3组工况下交错管束顶层和底层管束壁面温度进行对比.3组工况的空气流量均为0.8 kg/(m2·s)，喷淋水流量为1.92 kg/(m2·s).图6(a)为交错管束顶层壁面温度模拟结果与实验结果比较.结果表明，预测值的顶层管束壁面温度与实验值吻合度较好，最大误差仅为0.6%.图6(b)为交错管束底层壁面温度模拟结果与实验结果比较.结果表明，底层管束壁面温度预测值与实验值最大误差是进气温度ta,in=20.7 ℃，喷淋水温度tp,in=18.1 ℃工况，最大误差为1.1%.图7给出了管壁与喷淋水间Nusselt数模拟值与实验值的对比结果.结果表明，管壁与喷淋水间Nusselt数模拟值与实验值之间误差非常小，两者最大相差仅为0.54.

图6 管束壁面温度预测值与实验值对比结果(δ为两者之间的误差)Fig.6 Comparison of predicted and experimental values of tube bundle wall temperature (δ is the error between the both)

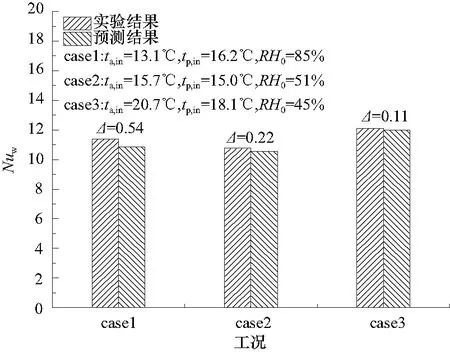
图7 管壁与喷淋水间Nusselt数模拟值与实验值的对比Fig.7 Comparison of Nusselt number between tube wall and spray water

为进一步验证模型准确性，又与文献[16]交错管束间水膜流动形态进行了对比，图8是交错管束外水膜流动规律的比较结果.结果表明，喷淋水滴撞击交错管束壁面后形成水膜，并且沿管束周向开始运动.当喷淋水膜所受重力、管束壁面对喷淋水膜剪切力及空气对喷淋水膜剪切力的合力不足以维持液膜黏附在管束表面时，水膜与管束发生分离，重新形成新水滴，这些水滴在管束底部大量集聚并流动，将形成如图8(a)所示的喷淋水在交错管束间流动形态.该流动形态与文献[16]实验所得喷淋水膜从管壁分离后的流动形态基本吻合，如图8(a)虚线所示.也就是说，该模型预测喷淋水在交错管束间流动形态与Killion等[16]实验结果基本吻合，进一步说明文中模型是可靠的.

图8 交错管束外水膜流动规律的比较结果Fig.8 Comparison of the flow patterns of water film outside staggered tube bundles

3 结果与分析

3.1 空气流量对传热传质的影响

为了揭示空气流量对交错管束间蒸发冷却传热传质的影响，模拟分析了空气流量1.2～2.8 kg/(m2·s)条件下交错管束间传热传质的变化.其他条件为进气温度18 ℃，相对湿度45%，喷淋水流量0.66 kg/(m2·s)，喷淋水温度18.1 ℃.图9为管束壁面平均温度、喷淋水膜-管壁间的Nusselt数(Nuw)、喷淋水蒸发量和喷淋水-湿空气间的Sherwood数(Sha)随空气流量变化的模拟结果.结果表明，增加空气流量可以提高交错管束间的传热传质性能.空气流量从1.2增至2.8 kg/(m2·s)时，管束壁面平均温度降低1.8 ℃，Nuw增大88%，喷淋水蒸发量增加37%，Sha增大67%.随着空气流量增大，喷淋水膜周围空气流速升高，管束壁面喷淋水膜湍流强度增大，进一步增大了喷淋水-湿空气界面与主流空气间水蒸气浓度差，从而强化了对流换热及传质性能.因此，可通过减小管间距的方法，提高管束间空气流速，强化管束壁面湍流强度，改善交错管束间传热传质性能.

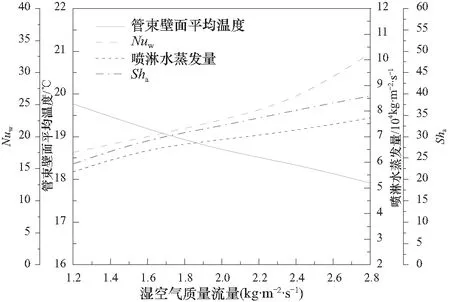
图9 管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随湿空气质量流量的变化Fig.9 The variation of the average wall temperature,Nuw,spray water evaporation and Sha with air flow rate

3.2 空气湿球温度对传热的影响

由于给定干球温度和相对湿度的情况下，空气湿球温度为唯一确定的.因此，在此部分模拟中，进气相对湿度变化范围为25%～85%，湿球温度为8.6～16.4 ℃.其他模拟条件：进气干球温度为18 ℃，喷淋水流量为0.66 kg/(m2·s)，喷淋水温度为18.1 ℃，空气流量为2.4 kg/(m2·s).图10给出了管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随湿球温度变化的模拟结果.

图10 管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随湿球温度的变化Fig.10 The variation of the average wall temperature,Nuw,spray water evaporation and Sha with wet bulb temperature

结果表明，管束壁面平均温度随进气湿球温度增大而升高，湿球温度升高1 ℃，管束壁面平均温度升高大约0.4 ℃；喷淋水膜-管壁间的Nusselt数(Nuw)随湿球温度增大而降低，这与WEI[26]和ZHENG[5]的研究结果类似.同时，喷淋水蒸发量随进气湿球温度增大而降低，湿球温度从8.6 ℃增至16.4 ℃时，喷淋水蒸发量降低61%.交错管束间传热传质性能降低的主要原因是，随着进气湿球温度增大，喷淋水膜-湿空气界面与主流气体间水蒸气分压力差降低.从而削弱了喷淋水膜与湿空气间传质驱动力，减弱了喷淋水膜与湿空气间的潜热换热，进一步降低了管束壁面与喷淋水膜间换热性能.湿球温度从8.6 ℃升至16.4 ℃时，水蒸气分压力从516.1 Pa升至1 754.6 Pa，增加了240%.因此，从图10可以看出，在Sha基本不变的情况下，随着进气湿球温度增大，喷淋水蒸发量也随之降低.

3.3 空气干球温度对传热的影响

本节分析了进气干球温度变化对交错管束间传热传质性能的影响，结果如图11所示.由于提高进气干球温度会降低喷淋水膜与湿空气间温差传热驱动力和传质驱动力，进一步降低管束壁面与喷淋水膜间换热性能.因此，随着干球温度升高，管束壁面平均温度显著上高.当干球温度从16 ℃上升至22 ℃时，Nuw平均降低43%；此外，喷淋水蒸发量随干球温度增大而降低，干球温度从16 ℃升至22 ℃时，喷淋水蒸发量降低10.5%.图11表明，Sha随干球温度变化较小.由于在给定进气相对湿度/湿球温度的情况下，进气干球温度越高，水蒸气浓度越高.因此，喷淋水蒸发量随干球温度升高而降低的主要原因是，随着干球温度的升高，喷淋水-湿空气界面与主流空气间水蒸气浓度差降低，削弱了传质驱动力.结合图10和图11可以看出，管束壁面平均温度、Nuw及喷淋水蒸发量随湿球温度变化斜率明显要比其随干球温度变化斜率大，也就是说，湿球温度对交错管束间传热传质性能影响比干球温度大.

图11 管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随干球温度的变化Fig.11 The variation of the average wall temperature,Nuw,spray water evaporation and Sha with dry bulb temperature

3.4 喷淋水流量对传热的影响

本节探究了喷淋水流量对交错管束间传热传质的影响.此部分模拟中，进气温度18 ℃，相对湿45%，喷淋水流量0.66～1.6 kg/m2·s，喷淋水温度18.1 ℃，空气流量2.4 kg/m2·s.图12给出了管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随喷淋水流量的变化结果.图12表明，喷淋水流量对管束壁面平均温度影响较小，此结果与Nuw随喷淋水流量变趋势是一致的.同时，Sha随喷淋水流量从7.2增加到9.5，增大了32%.这是由于，随着喷淋水流量增大，管束壁面水膜速度会适当增大，这将强化喷淋水膜与空气间对流作用，增强传质性能.结合图9和图12可知，与喷淋水流量相比，空气流量对交错管束间传热传质性能影响更显著，因此，可通过适当降低喷淋水流量的方法，降低循环水泵功率.

图12 管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随喷淋水流量的变化Fig.12 The variation of the average wall temperature,Nuw,spray water evaporation and Sha with spray water flow

3.5 喷淋水温度对传热的影响

本节分析了进气温度为18 ℃，相对湿度为45%，喷淋水流量为0.66 kg/m2·s，喷淋水温度为16～20.7 ℃，空气流量为2.4 kg/m2·s条件下，喷淋水温度对交错管束间传热传质的影响.图13给出管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随喷淋水温度的变化结果.结果表明，喷淋水膜-管壁间的Nusselt数(Nuw)和喷淋水蒸发量随喷淋水温度的升高而增大，同时，管束壁面平均温度与喷淋水温度成正相关.此外图13表明，喷淋水温度对Sha的影响较小，因此，在喷淋水温度变化不大的情况下，喷淋水温度对Sha的影响可以忽略不计.由于液体内部热运动与液体自身温度有关，液体温度越高，热运动越剧烈，水-气交界面附近离开水面进入气体的水分子越多.因此，随着喷淋水温度升高，喷淋水内部热运动更加剧烈，提高了喷淋水表面水分子进入喷淋水-湿空气交界面的速度，从而提高了喷淋水蒸发量.图13可以看出，增大喷淋水温度可以提高喷淋水膜-管壁间的Nusselt数(Nuw)和喷淋水蒸发量，但管束壁面平均温度/冷却水温度也随之升高.在制冷系统中，冷却水往往需要与冷水机组进行换热，因此管束壁面平均温度/冷却水温度升高意味着冷水机组性能减低，从而影响整个制冷系统的性能.

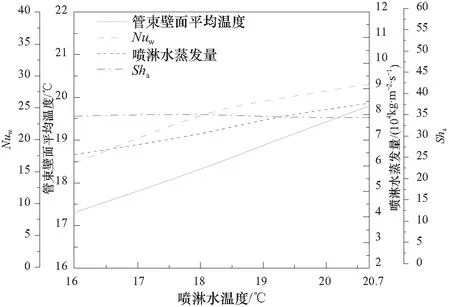
图13 管束壁面平均温度、Nuw、喷淋水蒸发量和Sha随喷淋水温度的变化Fig.13 The variation of the average wall temperature,Nuw,spray water evaporation and Sha with spray water temperature

4 结 论

文中采用基于DPM与WFM耦合的欧拉-拉格朗日方法，建立了外掠交错管束间湿空气-水蒸发冷却传热传质特性分析模型，通过模拟的方法，研究了运行参数：空气流量、湿球温度、干球温度、喷淋水流量及喷淋水温度对交错管束间湿空气-水蒸发冷却传热传质特性的影响.其结论如下.

① 与喷淋水流量相比，空气流量对交错管束间传热传质的影响更加显著，管束壁面平均温度随空气流量的增大而降低，但在改变喷淋水流量的情况下，管束壁面平均温度基本不变.因此，在空气流量不变及保证管束壁面完全润湿的情况下，可适当降低喷淋水流量，以降低循环水泵的功率.

② 增大湿球温度和干球温度会对交错管束间传热传质性能产生消极影响，当湿球温度升高1 ℃时，管束壁面平均温度将升高约0.4 ℃；当干球温度从16 ℃增至22 ℃时，管束壁面与喷淋水间Nusselt数(Nuw)将降低43%.与此同时，湿球温度对交错管束间传热传质性能影响要比干球温度对交错管束间传热传质性能的影响更加明显.

③ 喷淋水温度对交错管束间传热传质特性的影响规律比较复杂，管束壁面与喷淋水间Nusselt数(Nuw)及喷淋水蒸发量均随喷淋水温度升高而增大，但管束壁面平均温度也随之升高，这意味着管束内冷却水温度也将升高，使得冷水机组性能降低，从而影响制冷系统的性能.

④ 随着空气流量的增大，交错管束间空气流速及湍流强度也随之增强，从而强化了交错管束间传热传质性能.因此，可通过减小管间距的方法，提高管束间空气流速，强化管束壁面湍流强度，改善交错管束间传热传质性能.