面向光滑粒子流体动力学(SPH)流体的湍流细节模拟

班晓娟， 周靖， 王笑琨， 刘斯诺， 徐衍睿

(北京科技大学 计算机与通信工程学院, 北京 100083)

基于物理的流体模拟动画是计算机图形学领域的重要方面之一，流体模拟与交互是流体动画制作的核心问题，该类研究在游戏动画、虚拟现实等人机交互领域有着广泛的应用和较强的落地价值.

湍流细节模拟一直是流体模拟中的热点问题.SPH作为一种拉格朗日方法能够高效地模拟具有极大变形特征的流体，十分适合于模拟混乱的湍流.目前，许多研究通过强制不可压缩性[1-3]，解决了压强力求解的数值耗散问题. 然而，黏性力计算过程中的数值耗散问题仍然存在，使得诸如湍流等高频细节被平滑掉，极大地影响了实验结果的逼真度[4-5].

涡旋是湍流的主要组成成分，涡度是涡旋的重要属性之一，但传统的SPH方法很少考虑涡度场.物理学中将涡旋分为两类：刚体涡旋和无旋涡旋，见图1所示.在两种涡旋上分别放置两个刚性元件.图1(a)为涡旋像刚体一样旋转，具有非零涡度.图1(b)为无旋涡旋，除中心外涡度处处为0.刚体涡旋的涡度是角速度的两倍，而无旋涡旋除中心点外涡度处处为0.黏性力对流体粒子的旋转运动起主要作用，而用于描述流场内旋转趋势的涡度场并未被传统SPH方法纳入考虑.这就是在SPH方法中湍流细节损失的主要原因.

图1 刚体涡旋和无旋涡旋Fig.1 Rigid body vortexes and irrotational vortex

为了保持流体表面上的复杂湍流和涡旋细节，一些研究通过上采样方法，对表面点进行精细化处理[6]，增加表面分辨率.基于网格的方法使用自适应体积网格达成该目标[7].然而，以上方法都仅在表面添加细节，并没有考虑到流体内部运动.目前，机器学习方法被引入到流体模拟领域[8]，以实现高分辨率湍流的快速合成.但因为不规则的离散化，机器学习方法极难与基于粒子的方法结合.

Navier-Stokes方程在理论上能够准确地描述流体运动，但离散化过程仍会导致计算误差.在SPH方法中，N-S方程中的黏性力不能直接离散化并用于流体模拟，因此人工黏度被广泛地使用.黏性计算过程中的数值耗散将导致涡旋和湍流细节损失，然而目前只有少数研究涉及该类型的数值耗散.

为了解决上述问题，本文引入了一种基于黏性的湍流模拟方法，通过黏度计算过程中的能量耗散率来校正涡度场.借助流函数，利用涡度场的增强来提高速度，从而恢复逼真且可控的涡旋和湍流效果.该方案不仅可以增加现有的涡旋，还可以在潜在位置产生新的湍流.此外，涡度场的增强和速度的校正可与大部分类型的SPH方法兼容，且不影响随后的压力计算步骤.

1 相关工作

MONAGHAN用SPH方法解决了自由表面流动的模拟问题[9]，为流体模拟奠定了基础.随后MULLER等[10]提出使用理想气体状态方程来模拟流体，但其压缩性对结果造成了负面影响.BECKER和TESCHNER[11]提出了一种改进的弱压缩SPH (weakly compressible SPH)方法来降低压缩性，然而其效率受到时间步长的限制.HE等[12]和SOLENTHALER，PAJAROLA[1]提出了一种预测-校正方法，通过迭代步骤计算压强，保证流体的不可压缩性.这种思想也被应用在基于位置的流体模拟方法中(position based fluids, PBF)[13].IHMSEN等[2]遵循压力预测策略从而提出了隐式不可压缩SPH (implicit incompressible SPH, IISPH)方法.此外，BENDER和KOSCHIER[3]提出了一种强制零压缩和无发散速度场的方法.本文使用IISPH方法作为实验中计算效率和稳定性比较的基础.高频细节恢复问题一直以来都是流体模拟中的重要课题[14-16].对于欧拉方法，STAMS方案[17]首次将流体模拟引入计算机图形学中.然而，时间和空间的一阶精度使得该方法饱受数值耗散的影响.KIM等[18]对达到更高阶近似做出了贡献.

随后研究的混合方法进一步减少了数值耗散.ZHU和BRIDSONS[19]在不考虑某些旋转耗散的情况下，显著地消除了不可压缩流体的FLIP (fluid-implicit-particle)平流中数值耗散.JIANG等[20]使用混合方法恢复了流体大部分的旋转运动.虽然上面提到的模拟方法能够从宏观角度上处理这个问题，但欧拉方法和拉格朗日方法都难以模拟湍流等高频细节.因此，出现了一些专门用于模拟湍流细节的方法.这些方法可分为3大类，即上采样法，涡度限制法和拉格朗日涡旋法[21].

上采样法旨在粗离散化下添加高频率表面细节.MERCIER等[6]提出了一种独立的后处理方法: 在基于粒子的流体表面上施加细湍流.首先在曲率评估之后接种高分辨率表面点，然后在粗粒子上产生精细的表面波.之后，EDWARDS等[7]使用自适应间断法提出了一种基于网格的流体的自适应体积网格的方法.总之，上面提到的上采样法只能改善表面效果.一些机器学习方法也可应用于流体模拟领域，如卷积神经网络(CNN)[22]，能够在高分辨率源和粗糙模拟结果上合成精细湍流.

涡度限制方法旨在识别现有的涡旋并减少耗散.该方法通过添加新的强制项来增加目标位置的速度，并强制进行涡旋的旋转.LENTINE等[23]在中改进了涡度限制，同时保持了能量和动量的守恒.JANG等[24]使得涡度限制多层次化，从而获得更好的结果.尽管涡度限制方法是保留涡旋的简单方法，但是它无法产生额外的湍流细节.更重要的是，他们倾向于通过可调参数向系统添加过多的能量，这会违反能量守恒.

拉格朗日涡旋粒子法是建立在Navier-Stokes方程的涡度表示上的，理论上不受数值耗散的影响.该方法可通过粒子[25-26]，曲线[27]，细丝[28]和表面[29]实现湍流细节的捕捉与恢复，但难以处理边界问题，例如非刚性障碍物和自由表面等.ZHU等[30]提出了一种模拟运动物体周围涡旋细节的方法，但该方法需要借助欧拉网格实现.之后GOLAS等[31]处理欧拉网格上的边界问题.以上这些方法的另一个缺点是需求解Biot-Savart积分或矢量值泊松方程来恢复速度场.在2018年，BENDER等[21]提出了用于非黏性流体的微极元流体模型，该模型可以捕获流体粒子的微旋转并获得较好的湍流视觉效果.ZHANG等[32]提出了一种对流运动学的集成涡度(integrated vorticity of convective Kinematics, IVOCK)方法，通过计算平流中的涡度损失来恢复能量耗散.这些方法都是采用优化计算来恢复速度场的.受其流函数的启发，本文将其扩展到基于拉格朗日的流体模拟，能够从涡度场中得到速度的细化.

本文的方法可被视为拉格朗日涡旋方法.不仅可以增加现有的涡流，还可以在新涡流的潜在位置产生湍流.此外，方法不需要求解Biot-Savart积分或矢量值泊松方程.相反，借助流函数通过涡量场来细化速度，极大地提高了仿真效率.

2 基于SPH方法的流体模拟

在拉格朗日粒子描述下，流体粒子的加速度可表示为

(1)

(2)

(3)

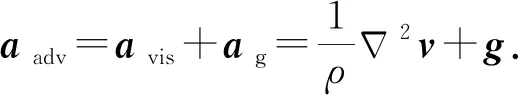
在传统的流体模拟中，N-S方程中的黏性项用于计算黏性力，可以按如下方式离散：

(4)

式中：d为维度；xij=xi-xj为粒子i和粒子j之间的距离；vij=vi-vj；h为支持半径；Wij为光滑核.因为拉普拉斯算子不适用于粒子系统，所以人工黏度被广泛采用.

由于人工黏度造成的耗散，流体系统的能量不断减小.某些区域的涡旋难以维持，丢失了许多细节.随着误差的累积，一段时间后会出现更明显的失真.为了保持这些细节，本文提出了基于黏性力校正的SPH湍流模拟方法.

3 基于黏度的涡度校正

本文方法与拉格朗日涡旋方法有密切关系：通过涡度恢复速度场.但本文通过流函数避免求解泊松方程，并利用黏度相关算法直接修改速度.在本文中，旋度场是通过粒子撞击前后黏性力导致的动能变化率来调整的.然后通过旋转场校正每个粒子的速度.该方法不仅可以放大现有的涡流，还可以在新涡流的潜在位置产生湍流.在本文方法中，涡度场的求解和速度的校正属于平流步骤，不影响随后的压力投影步骤，保证不可压缩性.

在本文算法中，除了速度之外，每个粒子都有一个涡度属性γ.涡度是用于描述局部位置的卷曲的矢量场.通常，它由速度场的旋度表示，在粒子系统中，涡度表示粒子旋转.离散化形式为

(5)

式中：m为质量；Wij为光滑核函数，在本文中使用3次样条函数.

在流动过程中，湍流和涡旋的细节由涡度场所展现的.无黏性流体只能在理想条件下存在.实际上，需要考虑黏性力对流体的影响.在传统的SPH方法中，黏性力的计算导致数值耗散，这造成了速度和涡度的计算误差.若不考虑黏性力,就无法准确描述流体的运动，在一些场景中许多细节如爆炸、搅动等将丢失.

3.1 针对黏性力影响的涡度校正

随着时间的推移，流体系统中的能量将在流体粒子之间转移.当粒子的速度发生变化时，涡度也发生变化并影响其运动轨迹.在此过程中，如果未计算涡度的特定值，或者未将其反馈应用于速度的纠正，则会丢失某些重要细节.在预测过程中，黏性力和外力影响着粒子的运动.一般情况下，外力是重力.因为重力没有旋转，所以本文方法只需考虑由黏度造成涡度所带来的速度变化，从而保持粒子的速度并且减少能量耗散.在流体粒子的运动过程中，它们受到相邻粒子的力的影响并导致速度的变化.这可归纳为图2两种情况.

图2 两种能量转换Fig.2 Two kinds of energy conversion

在平流-投影模型中，平流过程部分主要用于解决除压力之外的黏性力和外力.此时，由速度变化(黏性力造成)引起的能量增量和能量变化率平方根可表示为

(6)

(7)

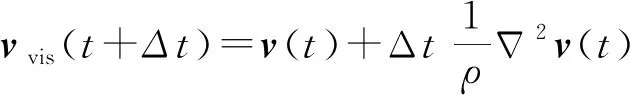
对于粒子系统，总能量可以表示为动能和势能之和，与热量无关.显然，粒子的动能是E=1/2mv2，其中一部分是可以用角速度表示，如图3.由于力的作用，粒子之间的碰撞将改变角速度.因为角速度能量是动能的一部分，在获得粒子的动能变化率之后,若将角速度表示的能量以相同的比率变化，则其值仍然在合理的范围内.对于由角速度表示的能量是E=Iω2，角速度的变化率可以表示为λ.

图3 角速度所携带的能量Fig.3 The energy carnied by the angular velocity

在物理学中，理想的涡旋可以分为两类: 刚体涡旋和无旋涡旋.其中，刚体的涡度是固定轴角速度的两倍，无旋涡旋的涡度处处为0.因此，涡度与角速度有一定的关系，并且至多等于角速度的两倍.当角速度增加P倍时，涡度也将增加f(P).涡度增量由以下函数表示

δγ=ηλγ

(8)

式中，δγ表示涡度校正，湍流水平增强参数η用于表示系统中涡旋的程度.参数越大，湍流效果越明显.

如图3所示，角速度所携带的能量是动能的一部分.当流体静止时，两种速度的能量都为0； 当只有线速度而没有角速度.此时，角速度能量为0，动能为E=1/2mv2，当流体旋转时，总动能为E=1/2mv2=Iω2，其中由角速度表示的能量等于动能.因此，角速度所表示的能量总是小于或等于动能.

3.2 从涡度增量获得速度增量

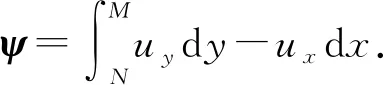
(9)

(10)

最后

(11)

现已在涡度场和速度场之间建立了联系.通过式(8)的黏性影响程度限制式(11)，避免增加的能量大于耗散能量.在三维空间，ψ和u可以分别设置为(ψx,ψy,ψz)和(u,v,w).

在传统方法中，需要求解泊松方程以将δγ转换为速度.Green函数提供了一种半解析解.在三维空间中表示为δφ=-ρ的泊松方程可以转换为

(12)

式中：φ为计算通量；ρ为密度.

通过亥姆霍兹分解以数学方式推广，流函数是速度场v的向量势.向量势ψ可以根据上面Green函数结果定义：

(13)

考虑到标量泊松问题：

ψx(p)=0,p→∞

(14)

所以可以使用以下离散化表达式进行空间离散化[30]：

(15)

式中：γj涡度；Vj为采样点体积；xi-xj代表第i个采样点和第j个采样点位置之间的距离.

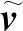
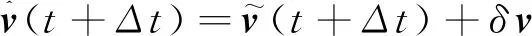
(16)

4 实验和讨论

在本节中，对本文方法在若干场景中进行了测试，与传统的IISPH方法和微极元方法(MP solver)[20]进行了比较.所有上述模型都与IISPH方法集成，密度误差控制在0.1%以内.此外，本文采用了AKINCI等[33]提出的边界处理方法.通过C ++实现基于物理的仿真及重构[34]框架，动画由Blender渲染.仿真平台为一图形工作站，采用Intel Xeon E5-2 637 v2 (15M高速缓存，3.50 GHz @ 4核心) CPU，80 GB RAM，NVIDIA Quadro M5 000 GPU.

4.1 参数η对湍流效果的影响

图4 左列分别显示了不同湍流水平控制参数η=0,0.2,0.4,0.6的模拟结果.随着η的增加，球体右侧的湍流效果逐渐变得丰富且在实验场景左侧的水面波纹显得更加细致.这说明本文方法可以使用可控参数恢复或添加的湍流细节.η作为一控制因子用于限制对于黏度造成的能量耗散的弥补，确保其不会过分增加能量，这样整个系统能量是趋于守恒的.较高的η值表示粗采样和大时间步长下的视觉效果.因此，在随后的对比实验中，本文方法中的参数均以0.6确保实验质量.实验还将本文方法与微极元方法进行了比较.图4 右列显示具有不同传递系数νt=0,0.2,0.4,0.6的微极元方法下的实验效果，可见人为地增加传递系数，并且在大参数情况下的湍流细节的丰富变化.但是，在相同的控制参数下，微极元方法的视觉效果并不像本文方法那么明显.此外，随着参数越高，数值不稳定性问题开始出现.当参数值大于0.6时，其数值计算结果不够稳定，开始出现无法控制的混沌湍流.因此，在随后的对比实验中，微极元方法中的参数均为0.4以确保稳定性.当控制参数η=0或νt=0时，算法可以被视为标准SPH方法，在本文中为IISPH方法.

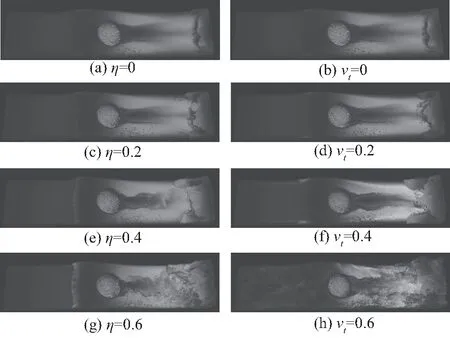
图4 本文方法和微极元方法Fig.4 This method and the MP solver

4.2 湍流模拟效果

图5展示了在1.072 M流体粒子情况下的传统IISPH方法和本文方法的模拟结果.在IISPH的模拟结果中，湍流细节的数量很快消失.在本文方法中，湍流更明显.特别是在接下来的两排中，球的左侧也有明显的波浪.本文方法更好地捕捉了湍流和涡旋细节.

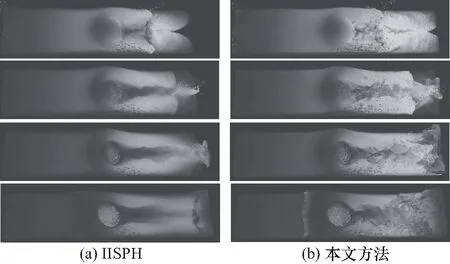
图5 IISPH下溃坝实验，传统方法和η=0.6的本文方法Fig.5 3D breakdam experiment under IISPH and our method with η=0.6

为了证明方法的稳定性和效果，实验使用动态边界条件模拟了两个复杂场景，并将本文方法与微极元方法进行了比较.在图6中，将木板缓缓放入水中然后横向移动.在这里，可观察到使用IISPH和微极元方法不会产生和保持复杂流动和湍流效应.与微极元方法相比，本文方法以物理上合理的方式增加能量，并在自由表面上产生逼真的湍流细节.此外，使用本文方法可以逼真地处理此场景中的高速的流体粒子和高度湍流运动，这证明了本文方法出色的稳定性.

图6 木板拨水实验，488 k流体粒子Fig.6 Board interacts with water containing 488 k particles

由于以前涡流或湍流方案倾向于增加过多的能量并且不稳定，实验进行了与2.9 M流体粒子交互的沉船实验.在图7中，船被放入水中然后逐渐下沉.船的巨大势能转化为流体粒子的巨大动能.当船落入水中时，水首先猛烈地运动，随着船沉没，水逐渐平静下来，最终达到稳定状态.在这个实验中，可发现使用IISPH和微极元方法产生了微弱的湍流细节，并且因为数值耗散，湍流效果很快丢失.相比之下，本文方法显示出更直观的运动，模拟出具有逼真的湍流效应的流体运动.当船沉没时，流体流动不会受到明显的阻碍.当船完全在水下时，有着明显的湍流和涡流.此外，随着时间的推移，流体逐渐平静下来，这意味着本文方法不会添加过多的能量.

图7 沉船实验Fig.7 Boat sinks into the water

这两个场景表明，本文方法可以在处理激烈碰撞等极端条件时保持稳定，并在物理上保留动能.且本文方法不仅放大了现有的涡旋，还产生了新的涡旋.此外，湍流细节的计算开销也保持在了合理范围内，表1列出了IISPH、微极元方法和本文方法在两个典型场景下的计算时间，与传统IISPH方法相比，MP方法与本文方法都相应增加了计算时间，部分场景下本文方法的计算效率优于MP方法.

表1 不同方法时间对比

5 结 语

本文提出了一种基于黏性的SPH湍流模拟方法，该方法从能量耗散中推导出涡度变化，从而恢复速度场.该方法可以显著地减少数值耗散，增加现有涡流并在潜在位置产生新的湍流.使用控制参数，可以很容易地控制湍流的精细度.实验证明，相比于传统SPH方法和微极元SPH方法，本文方法能更好地增强湍流效果.此外，即使使用大时间步长和大粒子半径，本文方法仍可以较好地保持能量，可以在极端模拟条件和复杂的大规模场景下稳健运行.目前实验表明其适用于不可压缩流体，但无数据证明该方法在其他种类流体中的稳定性.

未来计划将该方法扩展到其他流体，进一步研究微极元模型，并尝试将本文的模型与其合并，因为微极元模型在粗糙条件下显示出巨大的作用并且与黏度密切相关.此外将提高计算精度作为另一个研究方向.尽管离散流函数和涡量计算在某种程度上可以产生精细效果，但仍然可以找到具有有效且更精确的计算方法.