基于协作频谱感知的多无人机通信网络谱效优化研究
张宏伟, 达新宇, 胡航, 倪磊, 潘钰
(1. 空军工程大学 研究生院,陕西,西安 710077;2. 空军工程大学 信息与导航学院,陕西,西安 710077; 3.中国人民解放军95263部队,湖北,孝感 432600)
无人机因其广泛的应用前景而备受关注,常见应用场景包括:军事行动、监视侦察和荒野搜救等领域[1-3]. 装备有摄像机、传感器等通信设备的UAV,由于其自身的机动性和灵活性等特点,可用于辅助地面设备完成监视和侦察等任务. UAV在高速5 G网络和未来6 G网络中扮演重要角色[4],可实现网络连接向空中扩展,进一步为地面通信设备提供各种服务. UAV辅助通信具有快速、高效、低成本等优点,可有效缓解自然灾害和严重阴影等紧急场景下的通信问题[5]. 为充分利用UAV通信场景的潜在优势,UAV需要解决其频谱资源稀缺问题进而实现高效通信[6]. 近年来,UAV应用场景的工作需求已远超其现有承担能力,随着无线网络新设备的急剧增加,在UAV运行的非授权频段(例如:IEEE L波段、IEEE S波段和ISM波段)存在许多与之竞争的通信设备,如智能手机、手表等,其蓝牙和WiFi与UAV在频段内共存[7],对UAV的通信性能造成严重影响. 因此,频谱资源短缺、利用率低是UAV实现高效通信所面临的重要挑战之一[8].
认知无线电(cognitive radio,CR)技术作为解决当前无线通信领域频谱资源短缺最直接、最有效的手段,可以通过机会性地利用主用户(primary user,PU)授权频谱解决频谱拥挤问题[9],并且在推广5G、研发6G以及实现物联网(internet of things,IoT)技术等方面至关重要[10]. UAV安装传感器可以实现CR功能,在Interweave模式下,UAV作为次用户(secondary user,SU)通过频谱感知实时检测主用户发射机(primary transmitter,PT)状态,充分利用空闲频谱且避免主用户接收机(primary receiver,PR)被干扰中断,进而改善UAV通信网络性能[11]. 能量检测法具有易实现且不依赖PU先验知识的优点,因此在频谱感知中得到广泛应用,但是单用户感知场景受衰落和干扰等因素影响导致接收信号能量较小且检测性能不理想. 协作频谱感知(cooperative spectrum sensing,CSS)方法通过融合多个局部感知信息得出最终决策,可以有效克服隐藏终端问题[12],提升系统感知性能[13].
作为UAV高效通信性能的重要评价指标之一,频谱效率(spectrum efficiency, SE)的优化问题一直备受关注,但结合CR的UAV通信网络SE优化研究尚处于起步阶段. ZHANG[14]和PATRA等[15]研究了基于UAV辅助通信的移动中继系统,通过优化UAV飞行状态以及中继时间分配实现SE优化. HU等[16]基于UAV的位置信息,通过优化认知无人机网络(cognitive UAV network,CUN)中UAV发射功率等参数,有效提升了系统SE. LIU 等[17]研究了基于UAV的CR网络,为提高UAV系统SE性能,提出单UAV场景虚拟协作感知并建立感知时间和时隙数量的联合优化模型. 上述研究文献均针对单UAV场景展开,为解决传统单UAV场景频谱感知性能不理想及UAV应用场景SE较低的问题,本文提出基于多机协作的无人机通信网络SE优化模型,该模型充分考虑UAV在空地(air to ground,A2G)信道下的协作感知性能;研究多机协作场景下感知时间、判决门限以及UAV数量等参数的选取对系统平均SE的影响;最后提出高谱效联合优化算法,通过联合优化感知时间和判决门限以实现UAV次级认知网络SE最大化.
1 模型建立
1.1 系统模型
假设N架UAV以编队组网形式在某区域边界执行监控、侦察等任务,为提升SE,CUN在谱交织(interweave)模式下与主网络共享频谱. 微型旋翼无人机具有CR功能,可机会性利用空闲频谱. UAV作为SU实时检测授权频谱以避免对PU造成干扰,多个UAV协同工作,采用CSS方法提升感知性能. CSS帧结构如图1,其中帧结构数量为m,1帧内通信周期为T,感知时间为τ,每个UAV的报告时间为tr. 在感知阶段,所有UAV同时执行频谱感知;在报告阶段,UAV通过公共信道将局部感知信息依次报告至融合中心(fusion center,FC);在数据传输阶段,UAV依据FC判决结果决定是否接入PU授权频谱.
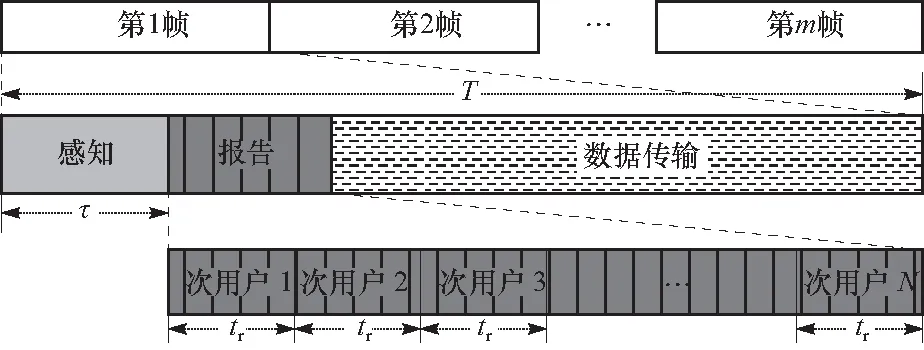
图1 CSS帧结构Fig.1 The frame structure of CSS
系统模型如图2,CUN由N架UAV编队组网构成,通过机间通信互联互通,在以主用户发射机(primary transmitter,PT)为中心的区域边界执行侦察任务,假设CUN侦察半径为RS. 在CUN中,所有UAV的飞行高度和速度均相等,分别定义为H和v,假设PT采用全向天线,UAV在区域边界的任意位置均可对PT状态进行局部感知;中心UAV内置FC,为节省公共信道带宽,所有局部感知信息采用时分多址(time division multiple access, TDMA)依次发送至FC,且FC采用硬判决融合(hard decision fusion,HDF)方式汇总感知信息,并对PT状态给出最终判决;为避免多个UAV同时传输数据造成同频干扰,在获得最终判决后,所有UAV占用授权频谱采用TDMA方式向次级用户地面接收机(secondary ground receiver,SGR)传输数据.

图2 认知无人机网络模型Fig.2 Cognitive UAV network (CUN) model
1.2 信号模型
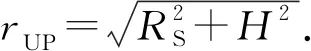
CUN的物理位置通过中心UAV的飞行弧度α进行度量,假设其初始位置弧度为α0,在第m帧时,飞行弧度为
(1)
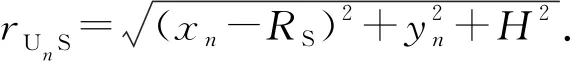
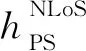
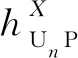
(2)
式中:θij为UAV与地面通信设备的仰角;ξ1和ξ2为环境特征参数. 由于无人机的飞行时间(以秒为单位)远高于信道相干时间(以毫秒为单位),因此无法研究瞬时信道实现的系统性能[19]. 此时主要关注信道的平均统计量,只考虑信道中的大尺度衰落,信道增益表达式为[19]
(3)
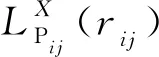
(4)
式中:f为载波频率;c为光速;LX为LoS或NLoS链路的平均附加损耗.
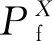
(5)
(6)
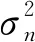

(7)
结合式(2)可得A2G信道下的虚警概率和检测概率为
(8)
所有UAV将本地决策信息报告至FC,FC根据“N中取k(k-out-of-N)”准则做出最终判决,k为FC判决门限. CSS的虚警概率QF和检测概率QD表达式如下
(9)
(10)
2 频谱效率优化
2.1 谱效优化问题
在本文图2所示模型中,假设CUN内所有UAV的传输功率为PU,PU空闲的概率用π0表示,PU存在的概率用π1表示,π0+π1=1. 根据UAV的频谱感知情况对其吞吐量分析如下.

情形2:UAV准确检测到PU存在,概率为π1QD,此时UAV不进行数据传输.
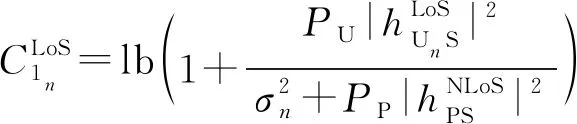
情形4:UAV出现虚警情况,错误检测到PU存在,概率为π0QF,此时UAV不进行数据传输.
在情形1和情形3中,UAV占用授权频谱进行数据传输,且由图1可知在1个帧结构内数据传输时间为T-τ-Ntr,假设将数据传输时间平均分为N段,每个UAV的数据传输时间tt相同,即tt=(T-τ-Ntr)/N,因此UAV次级网络的平均SE
式中:
(11)
(12)
SE优化问题可表述为
(13a)
(13b)
1∶QD=
(13c)
(13d)
(13e)
2.2 谱效优化方法
(14)
式中:
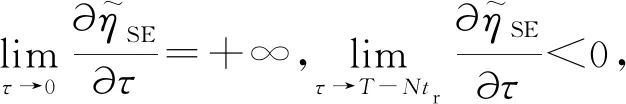
(15)
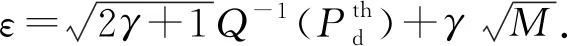
简化式(15)可得
Ψ(τ)=Z(τ)
其中
Ψ(τ)=ε2/2
(16)
(17)

证明式(17)中函数Z(τ)可重写为
Z(τ)=-ln[Z1(τ)z2(τ)]
(18)
式中:
对式(18)求关于τ的偏导
z1(τ)+z2(τ)
式中:
(19)
(20)
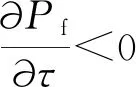

其根
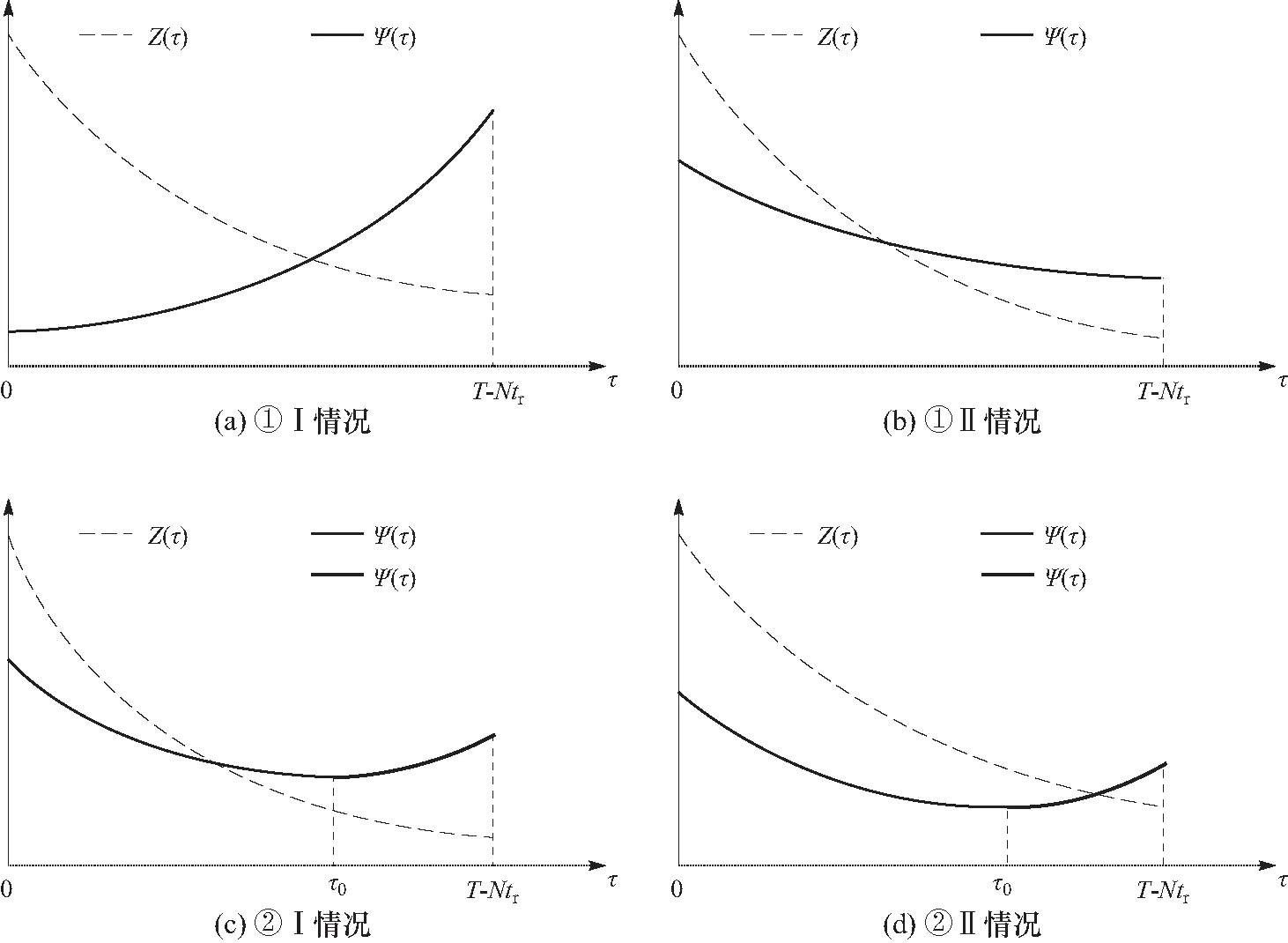
两者相交情况分析如下.
① 在区间τ∈(0,T-Ntr)内,函数Ψ(τ)单调:
I:Ψ(τ)单调递增. 如图3(a),两者只有1个交点.
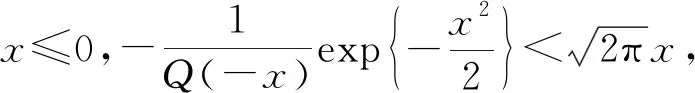
(21)
如图3(b),Ψ(τ)下降速度较慢,两者只有1个交点.
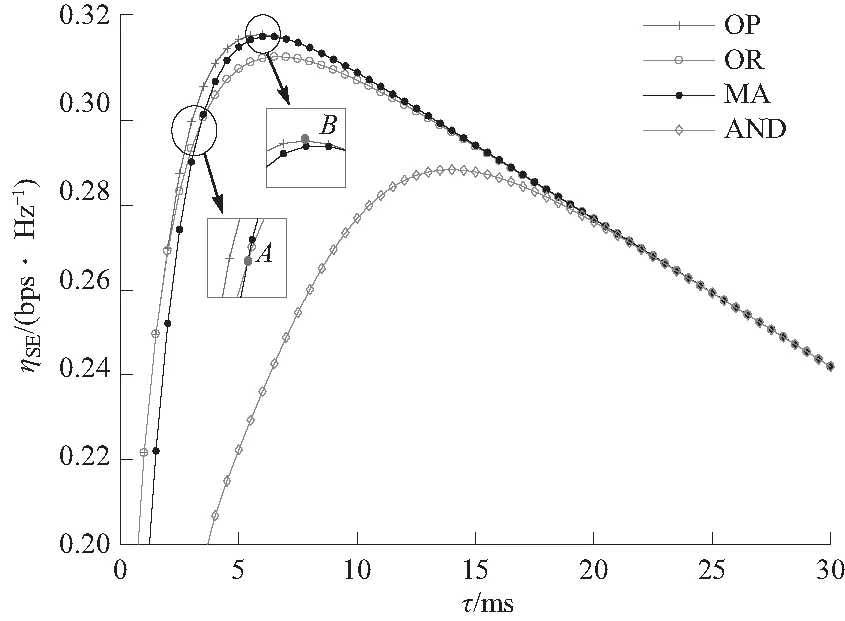
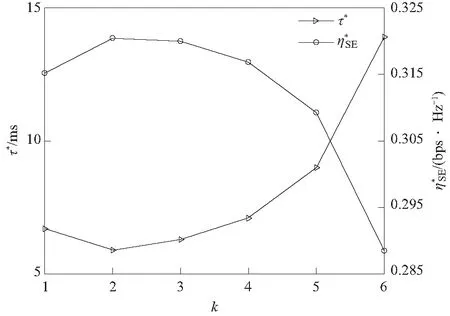
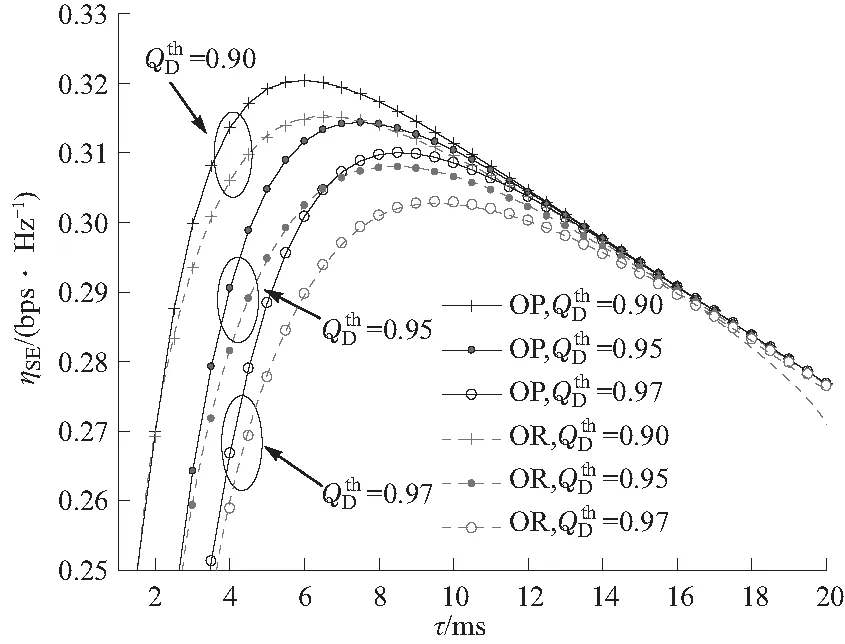
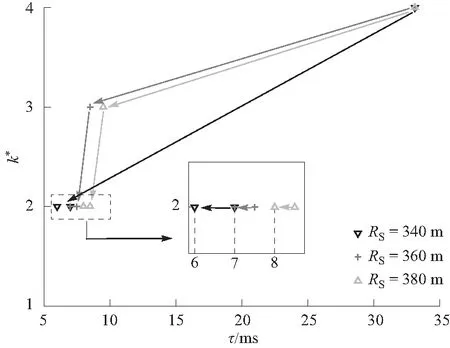
② 在区间τ∈(0,T-Ntr)内,Ψ(τ)为凸函数,非单调,其根τ0 II:交点位于区间τ∈[τ0,T-Ntr)内. 在该区间内,Ψ(τ)单调递增,Z(τ)单调递减,因此两者只有1个交点,如图3(d). 基于上述分析,可证明存在唯一τ*使UAV次级网络平均SE达到最优,利用Bisection算法可求得τ*. 图3 Ψ(τ)与Z(τ)的相交情况Fig.3 The intersection of Ψ(τ)and Z(τ) 表1 高谱效联合优化算法Tab.1 Joint optimization algorithm 本节给出数值仿真结果以验证SE优化方案和所提算法性能. 给定系统仿真参数除非有特殊说明,仿真参数如表2所示. 假设UAV的初始位置弧度α0=π/3,首先研究CUN在第1帧(α=α0)中感知时间和判决门限与SE的权衡关系. 图4展示了不同判决准则下感知时间对UAV次级网络平均SE的影响,证明存在唯一最优感知时间τ*使平均SE(ηSE)最大. 如图4所示,“Optimal(OP)”准则所获得的SE最大值为所有 表2 仿真参数Tab.2 Simulation parameters 图4 不同判决准则下SE与感知时间的关系曲线Fig.4 Spectrum efficiency versus sensing time under different decision rule 当FC判决门限k不同时,最优感知时间τ*和最优SE(η*SE)的变化情况如图5所示. 当k=2时,τ*最小,为6 ms,η*SE最大,为0.32 bps/Hz,与图4中点B处“OP”准则所取得的最优SE相同;在不同判决准则下,调整感知时间使SE均取最优时,可以发现与“AND”准则相比,其他准则可以获得较大的SE提升. 图5 最优感知时间和最优SE随FC门限的变化曲线Fig.5 Optimal sensing time and optimal spectrum efficiency versus decision threshold 图6 不同目标检测概率下SE与感知时间的关系曲线Fig.6 Spectrum efficiency versus sensing time under different cooperative target detection probability 图7展示了当QthD=0.90采用“OP”准则和“AND”准则时,UAV数量变化对SE的影响情况. 由图7可知,当感知时间较小时,N值的增加会明显提升感知性能使SE得到提升,且SE最大值也会随N的增加而增加,对应的最优感知时间τ*则会减少;当感知时间较大时,N值对感知性能的提升效果减弱且由于N值的增加会使数据传输时间减少,因此与N=10相比,此时N=6可以获得更大的SE;此外,在“OP”准则下,N=10时τ*=3.5 ms,此时SE最大值η*SE≈0.33 bps/Hz,与N=6相比可知:UAV数量的增加能够较好地实现SE性能提升,即通过较少的感知时间获得更高的SE最优值. 图7 不同UAV数量下SE与感知时间的关系曲线Fig.7 Spectrum efficiency versus sensing time under different number of UAVs 图8 高谱效联合优化算法收敛轨迹Fig.8 Examples of optimized trajectory of joint optimization algorithm 最后,研究在飞行过程中,CUN的飞行位置与SE的关系曲线,飞行位置通过帧结构数量m和飞行弧度α度量. 图9展示了不同判决准则下,给定感知时间时,SE与CUN帧结构数量的关系曲线. 随着CUN在侦察区域边界的持续飞行,CUN经历的帧结构数量m相应增加,且SE随m的增加呈周期性变化,结合式(1)和表2参数可知,CUN飞行1周经历的帧数量m≈2 136. 此外,图中点S对应CUN的初始位置(α0=π/3);点L处SE最低,对应CUN距离SGR最远的位置(α=π);点H处可获得整个飞行过程的最优SE,此时CUN距离SGR最近(α=2π). 图9 SE与帧结构数量m的关系曲线Fig.9 Spectrum efficiency versus the number of frames in CUN 本文针对UAV通信网络SE较低的现状,构建多机协作的认知无人机网络模型,研究了基于CSS的多UAV通信网络SE优化方案. 首先,分析多UAV在A2G信道下的协作感知性能,基于TDMA模式提出SE优化问题,证明SE是关于感知时间τ的单峰函数,且存在最优判决门限;接着,通过迭代优化感知时间和FC判决门限,提出解决SE优化问题的高谱效联合优化算法. 仿真结果表明,“OP”准则相较于其他准则可以获得更好的SE提升,“OR”准则和“MA”准则性能次优;提出的高谱效联合优化算法具有收敛性,能较好地实现UAV通信网络“高谱效”的优化目标. 该方法在基于多机协作的认知无人机网络SE研究中具有一定的实用价值.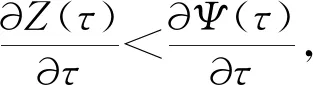


3 仿真分析

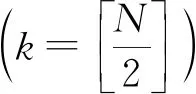
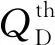

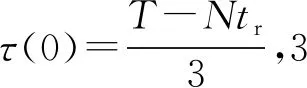

4 结 论

