夯实运算教学，发展运算思维

叶荟婕

【摘要】运算能力作为数学核心能力之一，伴随着学生一整个数学学习过程。其中，算理和算法是运算教学中的重难点，算理为计算提供了理论依据，算法让算理可操作化，在运算教学中，教师往往不知如何平衡算理和算法的教学。实际上，算理算法相互依存，借助直观模型让学生探索算理，感知算法是第一步;引导学生观察运算过程，明晰算理，辨析算法，突出竖式模型的建构是第二步;最终沟通理法，理清法明，才能真正理解算理，达到发展学生思维的最终目标。

【关键词】小学数学;算理;算法;运算能力

数学是一门研究数量关系的学科，其中运算能力是研究数量关系的基础，因此运算能力的培养一直受到广大教师的重视。《义务教育数学课程标准（2011年版）》中指出，运算能力是指能够根据法则和运算律正确地进行运算的能力，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。算理是算法的理论依据，为算法提供了正确的思维方式，而算法为算理提供了合理简便的操作过程，“理”“法”相互依存，相互联系。而大部分教师在运算教学中，对于算理的探索总是触及表面，更多地引导学生关注算法的探索，将算理与算法割裂开来，导致学生只会算，而不会举一反三，运算思维得不到发展。因此，在运算教学中，教师要根据教学内容及学生的认知情况，借助直观模型，引导学生在操作中自主探索算理，运用演绎推理的方式，归纳总结出简洁合理的算法，在说理的过程中沟通理法，达到理清法明的学习目标，才能从简单的掌握运算技能走向发展运算思维的最终目标。

一、探索算理，感知算法

小学生的思维方式还处于形象思维阶段，具有抽象性的算理是教学计算中的难点，想要突破难点，需要教师在日常教学中将抽象的算理借助直观模型展现出来，化抽象为直观，让算理变得可感知、可操作。教师在教学中，应避免触及表面的“假探索”，着重引导学生通过观察、操作、交流等活动独立探索、感知其中蕴含的算理，只有亲身体验的活动经验才能逐渐成为思维经验，最终抽象为算理，为后续建构算法打下基础。

例如，北师大版一年级两位数加一位数的进位加法一课，正是学生将直观转化为抽象运算的第一课，学生初次接触“满十进一”的进制问题，基于学生的学情，教师必须将“满十进一”的抽象算理蕴含在直观模型中。

师：28+4等于多少呢？请你用自己喜欢的方法摆一摆、拨一拨。

学生自主探究，学生可能会用小棒摆一摆。

生：我先拿出2捆小棒和8根小棒，再拿出4根小棒，8根和2根合起来是10根，将这十根捆在一起，一共有3捆和2根，所以28+4=32。

学生也可能会用计数器拨一拨。

生：我先拨在十位拨2颗珠子，个位拨8颗，表示28，再拨4颗，个位拨了2颗后，个位上有10颗珠子，十个一是十，所以把个位的十颗珠子拨走，在个位上拨1颗珠子，代表一个十，再在个位上继续拨2颗珠子，所以28+4=32。

把小棒扎成一捆，把个位上十颗珠子拨走，并在十位上拨一颗珠子，这两个动作其中就蕴含着“满十进一”这一算理，学生经历这两个操作后，让学生寻找相同点，进一步突出“满十进一”，化抽象为直观。通过直观操作探索算理后，再引导学生将刚刚的过程用竖式记录下来，这是将直观操作转化为抽象算法，让学生感知算法。只有引导学生关注直观操作中蕴含的抽象算理，才能真正让直观模型为抽象算理提供支撑。

二、明晰算理，辨析算法

数学的学习是学生在已有知识或者已有经验的基础上，通过归纳推理，总结出事物的一般性规律，是学生不断自我建构，自我生成的过程，运算教学也不例外。学生已有借助直观模型探索算理的活动经验，为进一步理解算理，教师要及时引导学生学会自我辨析、自我建构，在明晰算理的过程中，逐渐内化算理建构不同的算法，同时通过归纳推理，观察寻找不同算法之间的相同点，提炼出简便的算法即竖式模型，让学生经历辨析算法的过程，充分感悟不同算法之间的联系，体会竖式模型的必要性。

例如，北师大版三年级下册两位数乘两位数的竖式计算一课，这节课是乘法运算中的难点。

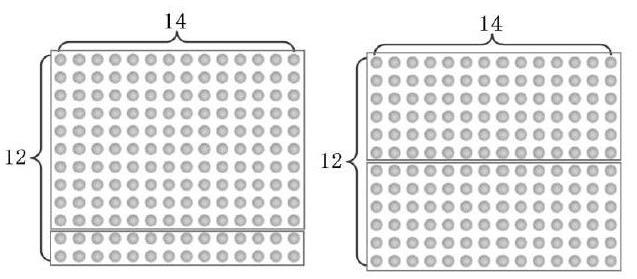
师：14×12到底等于多少呢？能不能用以前的知识解决，如果有困难，可以用点子图画一画哦，现在请你自己探究一下。

学生自主探究并汇报。

学生可能会出现这几种情况：

生1：我将12拆成10和2，先算14×10=140，再算2×14=28，再合起来140+28=168。

生2：我将12拆成6和6，先算14×6=84，兩个14×6的积相加，84+84=168。

还有的可能将12拆成3和9、4和8等等。

师：同学们用了这么多种方法来解决问题，请你观察这些方法，你有什么发现？

生：都是将12拆成一位数或者整十数，这样我们就能用以前学过的方法解决。

生：拆开后都分别和14相乘，再将两个积相加。

师：是的，你们都将其中一个数拆开，拆成我们学过的知识去计算，用已知解决新知。你们还发现了拆开后要分别和另一个数相乘，这也是乘法计算的道理，这么多种转化的方法，你认为哪种比较简便？

生：我认为将12拆成10和2，比较简便。

师：你们认为呢？接下来请你们根据观察的结果，将乘法的计算过程用竖式表示出来，并说出你的道理。

学生自主尝试。

在本节课中，根据已有知识，学生能根据点子图写出各种口算方法，也可以运用表格法计算出结果，说明学生已经能初步理解算理，并且能根据直观的点子图建构算法，因此寻找算法的共同点，最后抽象出竖式模型是本节课的难点。为了让学生能真正明晰算理，让学生的思考能围绕数学的本质，教师引导学生将新知转化为旧知后，再适度提升，让学生寻找最优的方法，从而突出乘法竖式模型的生长点。通过这样的教学，给学生的思维搭了一个脚手架，学生能调动旧知，去理解新知，在辨析算法的过程中，明晰算理，让学生从数学的本质上真正理解算理。