过共晶Ti-Si合金熔体电磁定向凝固过程实验和数值模拟

王均鹏，马文会，朱奎松，刑爱民，吕国强

(1.昆明理工大学 省部共建复杂有色金属资源清洁利用国家重点实验室，云南 昆明650093；2.昆明理工大学 真空冶金国家工程实验室，云南 昆明 650093； 3.昆明理工大学 冶金与能源工程学院，云南 昆明 650093；4.攀枝花学院，四川 攀枝花617000； 5.云南能投化工有限责任公司，云南 昆明 650093)

0 引 言

随着攀枝花地区钒钛磁铁精矿的不断开发利用，该地区累积了大量的高钛型高炉渣，其主要成分包括TiO2、SiO2、CaO、Al2O3、MgO等，炉渣基体矿物由钙钛矿和钛透辉石等组成[1-2].目前，高钛型高炉渣主要用于建筑材料制备，如矿渣砂、复合微粉、彩色路面砖等，高炉渣处理量与新增量持平，且造成渣中钛元素的浪费[3].为此，国内外学者对高钛高炉渣提钛展开了许多研究，如高钛型高炉渣改性-选择性富集钛钙矿、高温碳化-低温氯化工艺、湿法冶金(酸法和碱法)、高钛型高炉渣制备合金.但高钛型高炉渣改性-选择性富集钛钙矿工艺的钛回收率低、成本高等问题限制了其发展.高温碳化-低温氯化工艺大型化设备结构复杂、电耗高、氯化残渣难应用等造成投资大、推广受限.湿法冶金工艺在应用过程中面临着废酸和废碱等潜在的二次污染问题.高钛型高炉渣经过金属热还原可成功制备得到高硅钛硅合金，但由于高硅钛硅合金目前仅用于转炉炼钢的脱氧剂或合金剂，用量较少且附加值较低，因此需要迫切寻找高硅钛硅合金高效利用途径.Zhu等[4]通过电磁定向凝固的方法成功从高硅钛硅合金熔体中分离出初晶Si和Ti-Si合金.初晶Si进一步精炼提纯后有望作为太能级多晶硅的生产原料；Ti-Si共晶合金具有熔点低和流动性好等优良的铸造性能而被广泛研究[4].但由于定向凝固过程涉及到高温和电磁搅拌等极端条件，使得在解释相分离机理的过程中，缺乏以电磁定向凝固过程中的传热、流动和溶质等能量传递和传输过程为基础的认识.

本研究提出采用数值模拟技术对定向凝固过程中无法直接观察现象如熔体流动对初晶Si分离进行深入剖析，为深入探索高硅钛硅合金电磁定向凝固分离初晶Si和Ti-Si合金的机理奠定基础.目前，许多学者对定向凝固过程进行了数值模拟分析.Yu等[5]基于全局传热的耦合模型，对多晶硅定向凝固过程中熔体对流模式进行了研究，发现在向下的行波磁场作用下，电流参数对洛伦兹力、熔体对流和热场等有很大的影响，通过调整电磁参数可以提高熔体均一性，改善硅锭的质量.Chen等[6]在实验研究的基础上，建立了三维有限元模型用于对电磁定向凝固过程中熔池内的流场进行研究，数值计算结果表明，在不同电流频率参数下，熔体中的循环流动较为复杂，当频率从10kHz变化到100 kHz时，熔体的流动模式发生了改变，在较低频率的条件下，熔体中的循环流动占据的面积更大，涡流更加接近熔体的中心.Yang等[7]应用商业软件ANSYS建立了一个3D有限元模型，研究了TiAl合金熔体在定向凝固过程中水平流动对微观组织的影响，根据研究和计算可知，当功率过大时，熔体在固液界面附近的流速较大，实验结果也证明了此时晶体的连续生长受到干扰；而通过同时调整加热功率与电流频率，可以对熔体中的流场实现调控，得到有利于晶体连续生长的情况.高斯峰等[8]利用ProCAST软件以镍基单晶高温合金作为研究对象，对不同抽拉速率下合金凝固过程的温度场进行了模拟，根据计算得到的温度场分布，得到了固液界面前沿附近的液相，其温度梯度与抽拉速率之间联系.Yang等[9]的模拟计算结果表明，在电磁定向凝固过程中随着输入功率的增加，可以降低熔体中的径向温度梯度.

本文以Ti-89 wt.% Si合金为研究对象，结合合金熔体物性特点，以电磁场理论和定向凝固技术为基础，建立了电磁场-热场-流场三场耦合数学模型，并采用COMSOL Multiphysics 5.4商业软件(1056801)对不同工艺参数和电磁参数条件下熔体流场的变化规律进行数值计算.为了验证设计模型的合理性，设计了对应的实验对相关数值模拟结果进行了验证.

1 数学模型设计和实验设计

1.1 数学模型设计

图1为电磁感应定向凝固实验示意图.为了防止熔体和石墨坩埚被氧化，实验过程始终保持真空气氛.合金熔体在不同实验条件下进行定向凝固，下拉距离为5 cm.在定向凝固过程中，感应炉维持恒定加热功率.此外，使用非接触式红外温度计对凝固过程中熔体表面的温度进行测量.数值模型按感应炉实际尺寸1∶1建立，模型建立时进行了如下假设：

(a)电磁感应炉原理示意图 (b)二维轴对称模型和网格

1)考虑到电磁感应炉设备主要为对称结构，为简化计算，使用二维轴对称模型建模；

2)在整个实验过程中，炉内真空度始终<10Pa，为此忽略炉膛内气体对流换热对部件产生的影响；

3)假定坩埚内合金熔体的流动为不可压缩流动，钛硅合金熔体的各物性参数取常数计算；

4)模型中的辐射面均为漫灰表面[10].

1.1.1 电磁场基本控制方程

交变磁场对电磁定向凝固过程中流场及热场的影响是通过在合金熔体中形成的洛伦兹力实现的，而磁感应强度B和电流密度J由Maxwell方程组求解得到，表1列出了模拟计算中合金熔体的主要物性参数.

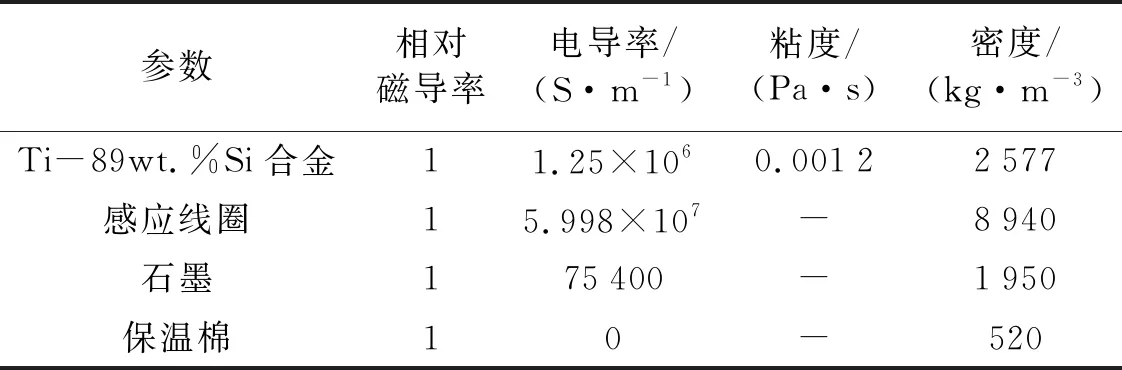
表1 模拟中使用的物性参数及常量

高斯定理：

(1)

法拉第电磁感应定理：

(2)

安培-麦克斯韦定理：

(3)

磁通量守恒定理：

(4)

本构关系为：

(5)

式中:D表示电位移矢量，E表示电场强度，H表示磁场强度，B表示磁感应强度，J表示传导电流密度矢量，ρe表示电荷体密度，ε0表示真空介电常数(8.854×10-12F/m)，εr表示合金熔体的相对介电常数，μ0表示真空磁导率(4π×10-7N/A2)，μr表示合金熔体的相对磁导率；σ表示合金熔体的电导率.

1.1.2 温度场基本控制方程

能量守恒方程为:

(6)

式中:ρ为合金熔体密度；Cp为合金熔体热容；k为热导率；u为流动速度矢量.

在上式中Q为感应涡流热源:

(7)

1.1.3 流场基本控制方程

对于不可压缩流体，连续性方程为：

(8)

动量方程(Navier-Stokes方程)：

(9)

合金熔体中受到的洛伦兹力以源项的形式添加到N-S方程中，即:F=J×B.

传输方程使用标准k-ε模型，湍动能(k)方程为：

(10)

湍动能耗散率(ε)方程为：

(11)

1.2 实验设计

实验用Ti-89 wt.% Si合金按其成分比例称取62.3g Si(高纯硅)和7.7g海绵Ti(>99.9%)，通过电磁感应炉熔炼制备，然后在下列实验条件下进行多次重复定向凝固实验，实验参数如表2所示.实验过程中使用非接触式红外温度计测量熔体表面中心的温度，从下拉开始测温，每隔10 min记录一次温度.

表2 实验方案设计

2 结果与分析

2.1模型验证

电磁定向凝固过程中，随着铸锭被下拉离开加热区，在底部循环冷却水和空冷共同作用，铸锭底部温度开始降低，这在铸锭的轴向会形成一个温度梯度.当铸锭温度梯度达到Si熔体开始结晶形核所需过冷度时，铸锭底部的Ti-89 wt.% Si合金熔体开始析出Si，并在铸锭底部富集.电磁定向凝固完成后，铸锭底部形成Si富集层，上部为Ti-75 wt.% Si共晶合金层.实验在功率为3.8 kW、频率为15 kHz和下拉速率为10 μm/s的实验条件下进行了定向凝固过程中的测温实验和数值模拟计算，通过对比测量与模拟得到铸锭轴向的温度梯度验证数值模型的可靠性.

图2(a)和(b)分别是定向凝固过程中合金熔体表面温度梯度和冷却曲线随下拉距离增加的变化曲线，其中温度梯度通过冷却曲线计算而得到.由图可知，两者的温度梯度曲线吻合较好，但由于数值模拟过程中保温棉的保温效果较实际情况要好，且在实验过程中循环冷却水温度有所升高，冷却效果降低，故模拟计算与实验测量的冷却曲线存在误差，其误差在8%以内.

(a)合金熔体表面的温度梯度 (b)合金熔体表面的温度

2.2 频率变化对初晶硅分离的影响

在相同下拉速率和功率的条件下，采用电磁场-热场-流场三场耦合模型，计算了线圈电流频率分别为15 kHz、30 kHz和50 kHz的定向凝固过程，其固相分数为0.50时熔体流场的分布(如图3所示)，图中流线表示熔体的流动方向及轨迹.

(a) 15 kHz (b) 30 kHz (c) 50 kHz

由图3可知，在频率为15 kHz的流场中可以观察到一个顺时针方向的涡流(取左半部分进行分析)，越靠近熔体外围流动越剧烈.此涡流的存在可以加强坩埚内上下部分熔体的混合，达到熔体成分均一化；而频率分别为30 kHz和50 kHz的流场，在其表面熔体的部分出现了回流现象.根据法拉第电磁感应定律可知，感应电动势大小为：

ε=-Ndφ/dt

(12)

随着线圈电流频率的增加，感应电动势增大，熔体中的感生电流也随之增大.通过模拟计算结果可知，当频率从15 kHz增加到50 kHz时，熔体中最大电流值出现在坩埚壁附近，从3.88×107A/m2增加到5.72×107A/m2，但熔体中心的电流密度从1 220 A/m2减小到4.63 A/m2.集肤深度及其对应深度位置的电流计算公式如下所示：

(13)

(14)

式中：δ为集肤深度；I0为熔体表面的电流密度(A/m2)；IX为熔体沿半径方向x处的电流密度(A/m2)；μe为合金熔体的磁导率；σf为合金熔体的电阻率；f为感应线圈的频率.由公式(13)(14)可知，在集肤效应的作用下，电流主要汇聚在熔体外围，越靠近熔体中心的电流密度越小.因此，洛伦兹力的渗透深度也在减小，进而轴向向下流动的熔体减少，熔体上部的硅原子向凝固前沿的传输过程受阻，而初晶硅的连续生长需要不断从熔体中获取硅原子[11].

图4为下拉过程中熔体平均速率随固相分数的变化，由图可知，在凝固前中期固相分数相同的情况下，随着电流频率的增大熔体中的流速呈下降趋势，而到了后期熔体的流动速率逐渐趋于一致，此时坩埚已逐渐远离线圈，熔体内的洛伦兹力均较小.在定向凝固过程中，熔体的平均流动速率减小意味着硅原子或团簇迁移的驱动力减小，凝固前沿的硅原子将减少.张玉峰等[12]在实验研究中证明了较低频率下铝硅合金的分离效果更好.故在较低的频率下进行实验有利于增强电磁搅拌效果，提高初晶硅的分离效果.

图4 不同频率下Ti-89 wt.% Si合金熔体的平均流速

2.3 功率变化对初晶硅分离的影响

图5是电磁定向凝固过程中Ti-89 wt.% Si合金熔体在功率分别为3.8 kW、4.6 kW和5.4 kW，固相分数为0.50时熔体的流场分布图.由图可知，不同功率下熔体的流型仍以顺时针方向转动为主(取模型的左半部分进行分析)，但功率为3.8 kW的熔体靠近表面中心的部分出现回流，通过2.2节的分析可知，熔体中的回流不利于溶质从熔体向凝固前沿传输；而随着功率的增加，回流现象减弱.由电磁场理论可知，坩埚中的感应电流和磁感应强度与线圈中的电流强度成正比，而实验室使用的电磁感应炉其功率的大小本质上是通过调节输入电流来控制的，所以功率的增加势必会增大熔体内的感应电流以及洛伦兹力.因此，增大功率有利于熔体形成轴向流动，进而实现初晶硅的连续生长.

(a)3.8 kW (b) 4.6 kW (c)5.4 kW

图6为不同功率下定向凝固过程中熔体的平均流速计算结果.显然，在凝固前中期某一确定的固相分数下，随着功率的增大，熔体的流动速率也不断增大；在后期不同功率下的流动速率趋于一致.因此，通过提高电磁感应炉的功率可以增加熔体的流动速度，增强电磁搅拌的效果，从而达到增强硅原子迁移的驱动力，保证初晶硅的连续生长.

图6 不同功率下Ti-89 wt.% Si合金熔体的平均流速

根据数值模拟结果，在功率为3.8 kW、4.6 kW和5.4 kW的条件下开展实验，用以验证过共晶Ti-89 wt.% Si合金电磁定向凝固过程中功率的变化对初晶硅分离富集效果的影响.将物料按质量百分比配置并放于高纯石墨坩埚中，然后在电磁感应炉中熔融，保温30 min后进行定向凝固，得到的铸锭沿轴向方向切割处理，最终得到纵向剖面图，如图7所示.由图可知，铸锭分为上下两部分，在其中间为分离界面(虚线表示)，铸锭分离界面上层为Ti-Si合金，下层则为硅富集层.

(a) 3.8kW (b) 4.6kW (c) 5.4kW

对不同功率条件下经过定向凝固得到的实验铸锭进行切割、打磨和抛光，在硅富集层中取不同铸锭纵截面同一高度位置的区域进行扫描电镜分析(图7中标记的点1、2和3)，结果如图8所示.根据研究表明灰色区域为硅相，而夹杂在硅相中的白色网络结构是Si+TiSi2相，即Si+TiSi2共晶成分[4,13].由图可知，随着功率的增加，网状白色结构的数量略有减少.通过前面模拟结果可知，在相同固相分数位置处，功率的增加会使熔体中的流动得到加强，剧烈的熔体流动有利于溶质的均匀分布.对于晶体生长而言，晶体的连续生长需要从熔体中获得足够的原子或者团簇.当熔体中的流动减弱，原子或者团簇迁移的驱动力随之减弱，从熔体扩散到液-固界面需要更长的时间，将导致晶体生长过程中原子或者团簇的供应不足.因此，提高功率以增强熔体的流动，可以在一定程度上使晶体连续生长所需要的原子或者团簇得到保证.取图7中的标记区域做XRF检测，其检测结果如图9所示.从图中可以发现，随着功率从3.8 kW增大至5.4 kW，硅富集层中硅的含量在增加，表明硅的富集效果得到加强.

(a)位置1 (b)位置2 (c)位置3

图9 不同功率下获得铸锭的硅富集层中Si含量

2.4 下拉速率对初晶硅分离的影响

图10所示为下拉速率分别为10 μm/s、30 μm/s和50 μm/s，固相分数为0.50时熔体的流场分布图.由图可知，随着下拉速率从10 μm/s增加50 μm/s，熔体始终存在一个沿顺时针方向转动的涡流，流型相似，在靠近熔体外围的部分其流动较为剧烈.

(a)10 μm/s (b)30 μm/s (c)50 μm/s

为了更加直观地认识不同下拉速率下流速的变化趋势，对定向凝固过程中熔体的平均流速进行计算，结果如图11所示.显然，在固相分数相同的条件下，下拉速率越大，熔体的流动速率越小.在电磁定向凝固过程中，当坩埚逐渐远离加热区，熔体中的磁场将逐渐减弱，其受到的电磁力也相应减小，从而导致熔体流动速率减小，硅原子迁移的驱动力减弱.此外，下拉速率的增加将使熔体中硅原子迁移的时间减短，且凝固前沿没有充足的时间吸收硅原子[4].

图11 不同下拉速率下Ti-89 wt.% Si合金熔体的平均流速

同理，其他条件不变情况下在下拉速率分别为10 μm/s、30 μm/s和50 μm/s开展Ti-89 wt.% Si合金电磁定向凝固实验，制备得到的铸锭其纵向剖面的宏观图如图12所示.由图可知，铸锭分为上下两部分，图中虚线表示分离界面，铸锭分离界面以上的部分属于Ti-Si合金，剩余部分则为硅富集层.

(a) 10 μm/s (b) 30 μm/s (c) 50 μm/s

对图12中标注的区域进行扫描电镜分析，微观组织形貌图如图13所示.显然，在图13中也观察到网状的白色结构，且随着下拉速率的增大，夹杂的网状白色结构增多.根据图11可知，随着固相分数的增加，熔体的流动速率逐渐减弱，熔体中的Si原子向固液界面迁移受阻，同时，随着下拉速率的增加，凝固前沿吸收Si原子的时间变短.因此，凝固前沿无法从熔体中获取足够Si原子供初晶Si生长，Ti-Si共晶合金熔体将被凝固前沿吞没，最后在晶体间偏析形成TiSi2相.通过XRF检测图12硅富集层中标记区域的硅含量，结果如图14所示，下拉速率为10μm/s时硅含量为93.96wt.%，随着拉速的增加硅富集层中硅含量逐渐减少.

(a)位置1 (b)位置2 (c)位置3

图14 不同下拉速率下获得铸锭的硅富集层中Si含量

3 结 论

通过建立Ti-89wt.%Si合金熔体电磁定向凝固过程中的电磁场-热场-流场等多物理场耦合模型，研究了在不同工艺参数和电磁参数下熔体流场对初晶硅分离的影响，得到以下结论：

1)由于集肤效应的影响，当电流频率为15 kHz时，电磁力对熔体的搅拌能力最强导致熔体的平均流速达到最大，此时最有利于硅相富集.

2)熔体的平均流速随着功率的增大而增大，当功率为5.4kW时，硅富集层的硅含量达到95.84%，此时硅相与合金的分离效果最好.

3)随着下拉速率的增大，熔体的冷却速率增大而平均流动速率减小，导致凝固前沿吸收的硅原子或者团簇减少，硅相的分离效果变差，硅富集层含量降至88.04%.