环Fq+v Fq上线性码的重量计数器
齐 薇, 廖群英
(四川师范大学 数学科学学院,四川 成都610066)
众所周知,纠错码在增强信息传输可靠性方面起着非常重要的作用,它可以用来检测和纠正信息传输中的错误[1].线性码是一类具有良好代数结构的纠错码[2-3],线性码的重量分布是检测译码错误的重要指标,重量计数器是研究线性码的重量分布的一种有力工具.
1977年,MacWilliams等[4]对有限域上码的各种重量计数器及其关系进行了较为系统的阐述.自此之后,许多学者将研究兴趣从有限域转移到有限环.2012年,田园等[5]定义了环

上线性码的t-Lee重量计数器,给出了该环上线性码的t-Lee重量计数器的MacWilliams恒等式.2014年,许和乾等[6]定义了环

上线性码的对称重量计数器,并且建立了该环上线性码的Hamming重量计数器和Lee重量计数器的MacWilliams恒等式.2017年,Chen等[7]定义了环

上的线性码,研究了一些重量计数器并获得了这些重量计数器之间的关系,其中p是素数.关于线性码重量计数器的更多研究成果参见文献[8-14].
本文定义了R上线性码C的长度重量计数器,得到线性码C的Lee重量计数器和Hamming重量计数器均可由长度重量计数器表示.
1 R上线性码的基本性质
设交换环

其中,p是素数,m为正整数.Rn的非空子集C称为是R上码长为n的码;若C是R-子模,则称C为R上的线性码.设C1、C2是R上码长为n的线性码,则

也是R上码长为n的线性码,称C1+C2为C的分解.进而,若

文献[15]中给出了R上的线性码C与Fq上线性码C1-v,Cv是相互唯一确定的,即如下引理.
引理1.1[15]设C为R上码长为n的码,C1-v、Cv如上给出,则:
1)C是R上的线性码,当且仅当C1-v、Cv是Fq上的线性码,且C=vC1-v+(1-v)Cv.
2)设C是R上的线性码,则

且分解唯一.
为建立R上的线性码和Fq上线性码之间的联系,下面给出Gray映射和R上对偶码、自正交线性码、自对偶线性码及LCD线性码的定义.
定义1.2定义Rn到F2nq的Gray映射为

进而,若x◦y=0,则称x、y正交.
2)R上码长为n的线性码C的对偶码C⊥定义为

若C⊆C⊥,则称C为自正交线性码;若C=C⊥,则称C为自对偶线性码;若C∩C⊥=0,则称C为LCD线性码.

因C为R上码长为n的线性码,故不妨设


另一方面,由Φ是双射可知

推论1.5设C是R上码长为n的自正交(自对偶,LCD)线性码,则Φ(C)也是Fq上码长为2n的自正交(自对偶,LCD)线性码.
证明由Φ的定义易证Φ(C)是Fq上长为2n的码.再由C⊆C⊥知

于是,由命题1.4可得

从而Φ(C)是Fq上长度为2n的自正交线性码.其他情形可类似证明.
2 R上线性码的重量计数器
在编码理论以及工程实现中,线性码的重量计数器是一个重要的参数,它是检测译码错误概率的主要依据.迄今为止,最受关注的是Lee重量计数器和Hamming重量计数器.然而,由这2个重量计数器不容易得到有关线性码的直和分解,由此引入长度重量计数器的概念.下面首先给出R上线性码的Lee重量及一些重量计数器的定义.
定义2.1设C是R上码长为n的线性码.
1)对r=x+vy∈R,定义r的Lee重量为

3)对任意c′,c″∈Rn,定义c′与c″的Lee距离为dL(c′,c″)=wL(c′-c″);
4)环R上码C的最小Lee距离定义为
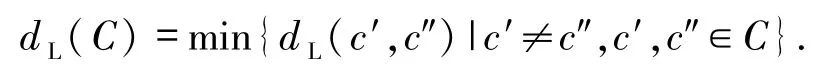
由此定义可知,Rn中任意向量的Lee重量值取自集合{0,1,…,2n},从而引进重量计数器的概念.
定义2.2设C是R上码长为n的线性码.
1)对任意i=0,1,…,2n,记Li为C中Lee重量为i的码字个数,称集合{L0,L1,…,L2n}为码C的Lee重量分布.码C的Lee重量计数器定义为

3)对任意i=0,1,…,n,记Hi是C中Hamming重量为i的码字个数.称集合{H0,H1,…,Hn}为码C的Hamming重量分布.码C的Hamming重量计数器定义为

由上述定义可得
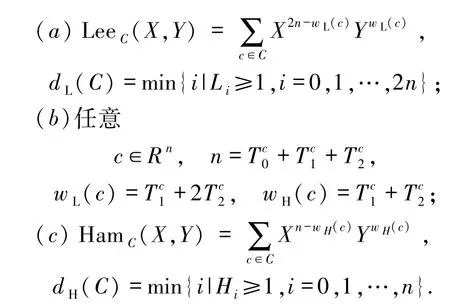
根据文献[4],记dH为码C的Hamming距离.
引理2.3设Φ为Rn到F2nq的Gray映射,则:
1)对任意z∈Rn,有wL(z)=wH(Φ(z));
2)Φ是(Rn,dL)到(F2nq,dH)的保距同构映射.
证明1)根据定义2.1可得.
2)容易证明Φ是Fq-线性同构.进而,对任意x,y∈Rn,有

即Φ是保距映射.
下面的定理2.4表明R上线性码C的对称重量计数器可以用来表示Lee重量计数器和Hamming重量计数器.
定理2.4设C是R上码长为n的线性码,则
1)LeeC(X,Y)=SweC(X2,XY,Y2);
2)HamC(X,Y)=SweC(X,Y,Y);
3)LeeC(X,Y)=HamΦ(C)(X,Y).
证明只需证明1)、2)和3)类似可得.由定义2.2的1)和2)可知

由定理1.1可知,R上线性码C的直和分解形式为C=vC1-v⊕(1-v)Cv.为了建立R上线性码C、vC1-v和(1-v)Cv三者重量计数器的联系,下面定义一种新的重量计数器.
定义2.5R上码长为n的线性码C的长度重量计数器定义为


由定义2.1可知,对任意r∈R,wL(r)的值取自集合S={0,1,2}.对任意

下面的引理2.6表明R上线性码C的对称重量计数器也可由长度重量计数器表示.由命题2.4,对称重量计数器可以表示出Lee重量计数器和Hamming重量计数器.从而,Lee重量计数器和Hamming重量计数器均可由长度重量计数器表示出来.
引理2.6设C是R上码长为n的线性码,则Ω(LweC(X0,X1,…,Xn-1))=SweC(X0,X1,X2).
证明 由长度重量计数器和对称重量计数器的定义及(3)式,可得

引理2.7设C=vC1-v⊕(1-v)Cv是R上码长为n的线性码,则

证明设c=(c0,c1,…,cn-1)=a+b∈C,其中

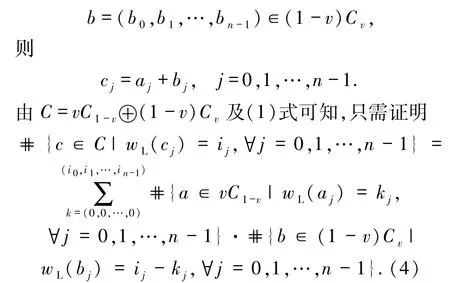
下面对码长l进行归纳.
1)当l=1时,由c=a+b∈C,其中

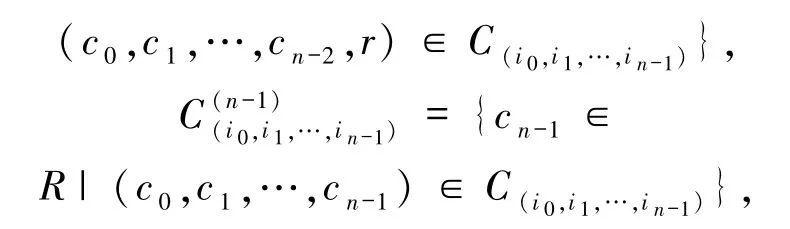
则由(1)和(5)式可知



