非对称Keyfitz-Kranzer方程组在压力消失过程中的质量集中和空化现象

方艳红， 郭俐辉

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐830046）

研究一类经典的双曲守恒律方程组

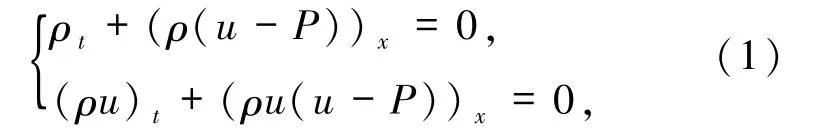
其中ρ、u和P分别表示密度、速度和压强.该系统是非对称Keyfitz-Kranzer方程组［1］的特殊形式，广泛应用于弹性力学和流体力学等领域.它也可以通过Aw-Rascle交通流模型［2］得到，而交通流广泛应用于描述交通事故以及其他交通现象的形成.

近年来，非对称Keyfitz-Kranzer方程组已被学者们广泛研究.文献［3］运用补偿紧性法估计了Keyfitz-Kranzer方程组黎曼不变量的边值问题，并证明其Cauchy问题全局有界熵解的存在性；文献［4］构造了Chaplygin气体非对称Keyfitz-Kranzer方程组的黎曼解；文献［5］对广义和修正Chaplygin气体非对称Keyfitz-Kranzer方程组的黎曼解及其解的极限行为进行了研究；文献［6］讨论了多方气体与广义Chaplygin气体非对称Keyfitz-Kranzer方程组的压力消失极限；文献［7］研究了多方气体非对称Keyfitz-Kranzer方程组的压力消失以及流扰动极限行为.关于Keyfitz-Kranzer方程组的更多研究可参见文献［8-9］.

为了与宇宙观测数据一致，文献［10］在2014年提出扩展Chaplygin气体模型

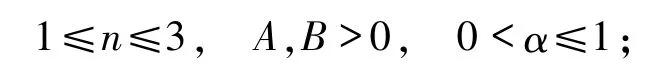
更多研究请参看文献［11］.扩展Chaplygin气体由2项组成：第1项是服从线性正压状态的普通流体，第2项与能量密度的倒数有关.它可以通过改变重力精确地研究宇宙加速度.本文研究α=1的特殊形式

也称为输运方程，可以通过Boltzmann方程［14］得到.输运方程（3）通常用来描述一些重大的物理现象，如自由粒子在碰撞作用下的黏附过程［15］以及宇宙中大规模结构的形成［16］.本文主要通过从方程组（1）到（3）的压力消失极限过程研究宇宙2个不同时期之间的过渡.

本文首先研究带有如下初值

的方程组（1）和方程（2）的黎曼解的极限.容易得到，压力消失过程中，激波和接触间断构成的解收敛到一类特殊的δ激波，其传播速度和权与零压流不同，且中间密度趋于奇异测度.另一方面，疏散波和接触间断构成的解收敛到接触间断，中间状态趋于真空.因此，方程组（1）不会收敛到零压流（3）.

为解决此问题，引入扰动Keyfitz-Kranzer方程组

与方程组（1）相比，方程组（5）的2个特征真正非线性，即黎曼解由疏散波和激波组成.压力消失时，2个激波构成的解收敛到零压流的δ激波，2个疏散波构成的解收敛到接触间断，且中间状态趋于真空.因此，扰动Keyfitz-Kranzer方程组（5）收敛到零压流（3）.不难发现，质量集中会导致狄拉克激波的出现，而真空状态是由空化现象引起的.

1 输运方程的黎曼解

本节简要叙述零压流（3）的黎曼解，具体参看文献［12］.方程组（3）有特征值λ=u和对应的右特征向量r=（1，0）T，满足▽λ·r=0.

对于u-＜u+，带有真空状态的2个接触间断解为

此外，δ激波解（7）和（8）满足广义Rankine-Hugoniot条件

和熵条件u+＜σδ＜u-.

2 Keyfitz-Kranzer方程组黎曼解的极限行为

2.1 方程组（1）的黎曼解本节简要叙述方程组（1）（2）和（4）的黎曼解.不失一般性，取A=B=1.方程组（1）有2个特征值

故方程组（1）严格双曲（λ1＜λ2）和一类特征真正非线性、二类特征线性退化.

除常数解，奇解为疏散波

这里疏散波曲线和激波曲线在（ρ-，u-）点重合，故方程组（1）属于Temple class［17］.（ρ，u）相平面被划分为Ⅰ、Ⅱ区域，方程组（1）（2）和（4）的黎曼解构造如下：

2.2 ε→0时，方程组（1）的黎曼解的极限本节研究方程组（1）的解的压力消失极限，并与零压流（3）的解做比较.

2.2.1 δ激波的形成 当u-＞u+时，由激波和接触间断构成的黎曼解为

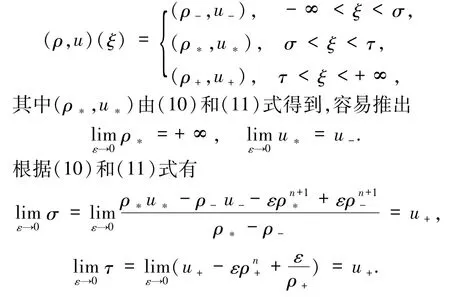
意味着S1和J收敛到一类特殊的狄拉克激波［18］，其传播速度u+不同于零压流（3）.

由（10）和（11）式得

与零压流（3）的权不同，可能是由于δ激波的传播速度不同导致的.对于方程组（1）的极限解，δ激波左侧特征进入δ激波曲线x=u+t，而右侧特征与δ激波曲线平行.对于方程组（3），δ激波两侧特征全部进入δ激波曲线x=σδt（见图1）.由于方程组（1）的极限解不满足熵条件u+＜σδ＜u-，所以方程组（1）的黎曼解不会收敛到零压流（3）.

图1 物理平面Fig.1 Physical plane

2.2.2 真空状态的形成 当u-＜u+时，包含疏散波和接触间断的黎曼解为

由（9）和（11）式推出

因此，疏散波曲线R1趋于速度为u-的接触间断J1，而接触间断J趋于速度为u+的接触间断J2.与此同时，中间状态趋于真空，故方程组（1）的黎曼解收敛到零压流（3）.

3 扰动Keyfitz-Kranzer方程组黎曼解的极限行为

3.1 方程组（5）的黎曼解本节构造方程组（4）和（5）的黎曼解.不失一般性，取A=B=1.方程组（5）有2个特征值

因此，方程组（5）严格双曲（ρ，u＞0），2个特征真正非线性.

由于方程组（4）和（5）在

下是不变量，寻找自相似解

则方程组（4）和（5）变成常微分方程无穷远处的边值问题

对（21）式的第二式左右两边取极限

即S2与ρ轴有交点.

通过上述分析，给定负状态（ρ-，u-），将（ρ，u）半平面分成5个区域Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ（见图2）.方程组（4）和（5）的黎曼解构造如下：

图2 基本波曲线Fig.2 The curve of elementary waves

1）（ρ+，u+）∈Ⅰ（ρ-，u-）：R1+R2；

2）（ρ+，u+）∈Ⅱ（ρ-，u-）：R1+S2；

3）（ρ+，u+）∈Ⅲ（ρ-，u-）：S1+R2；

4）（ρ+，u+）∈Ⅳ（ρ-，u-）：S1+S2；

5）（ρ+，u+）∈Ⅴ（ρ-，u-）：R1+V真空+R2.

3.2 ε→0时，扰动方程组（5）的黎曼解的极限情况本节分析方程组（5）的黎曼解的极限行为并与方程组（3）的黎曼解做比较，分2种情况讨论.

3.2.1 δ激波的形成 当u-＞u+时，有

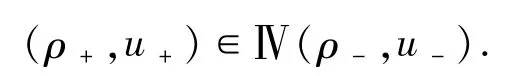
给定任意ε＞0，（ρ*，u*）为中间状态，S1连接（ρ-，u-）和（ρ*，u*），而S2连接（ρ*，u*）和（ρ+，u+）.具体来说，有

定理3.4当u-＞u+时，假设（ρ，u）（ξ）是方程组（4）和（5）由2个激波构成的黎曼解.压力消失过程中，激波解在分布意义下收敛到δ激波解（7）和（8），与零压流（3）的黎曼解完全相同.此外，ρ和ρu的极限分别是

3.2.2 真空状态的形成 当u-＜u+时，（ρ+，

u+）∈Ⅰ∪Ⅴ（ρ-，u-）.给定任意ε＞0，（ρ*，u*）为中间状态，R1连接（ρ-，u-）和（ρ*，u*），R2连接（ρ*，u*）和（ρ+，u+）.

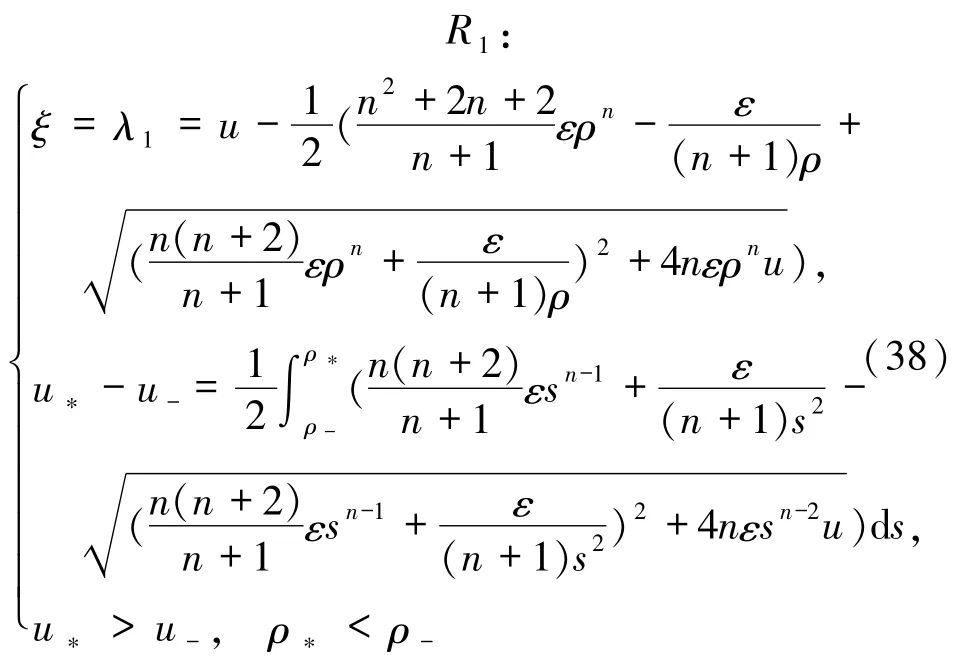
定理3.5当u-＜u+时，假设（ρ，u）（ξ）是方程组（4）和（5）由2个疏散波构成的黎曼解.压力消失时，疏散波收敛到接触间断，中间状态趋于真空，与零压流（3）的黎曼解完全相同.

证明假设

4 数值模拟

本节利用Lax-Friedrichs差分格式呈现一组具有代表性的数值实验去验证δ激波和真空状态的形成.

1）当u-＞u+时，取初始数据

对于t=0.4的情形，图3～图5的左侧分别呈现了

的数值结果，表明压力消失过程中质量集中导致δ激波的形成.

2）当u-＜u+时，给出初始数据

对于t=2的情形，图3～图5的右侧分别呈现了

图3 ε＝1时δ激波（左）和真空状态（右）的密度Fig.3 Density ofδshock wave（left）and vacuum states（right）forε＝1

图5 ε＝0．000 1时δ激波（左）和真空状态（右）的密度Fig.5 Density ofδshock wave（left）and vacuum states（right）forε＝0．000 1

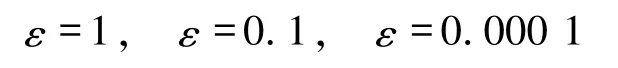
的数值结果，表明压力消失过程中空化现象导致真空状态的形成.

综上所述，以上所有的数值实验与理论分析完全一致.

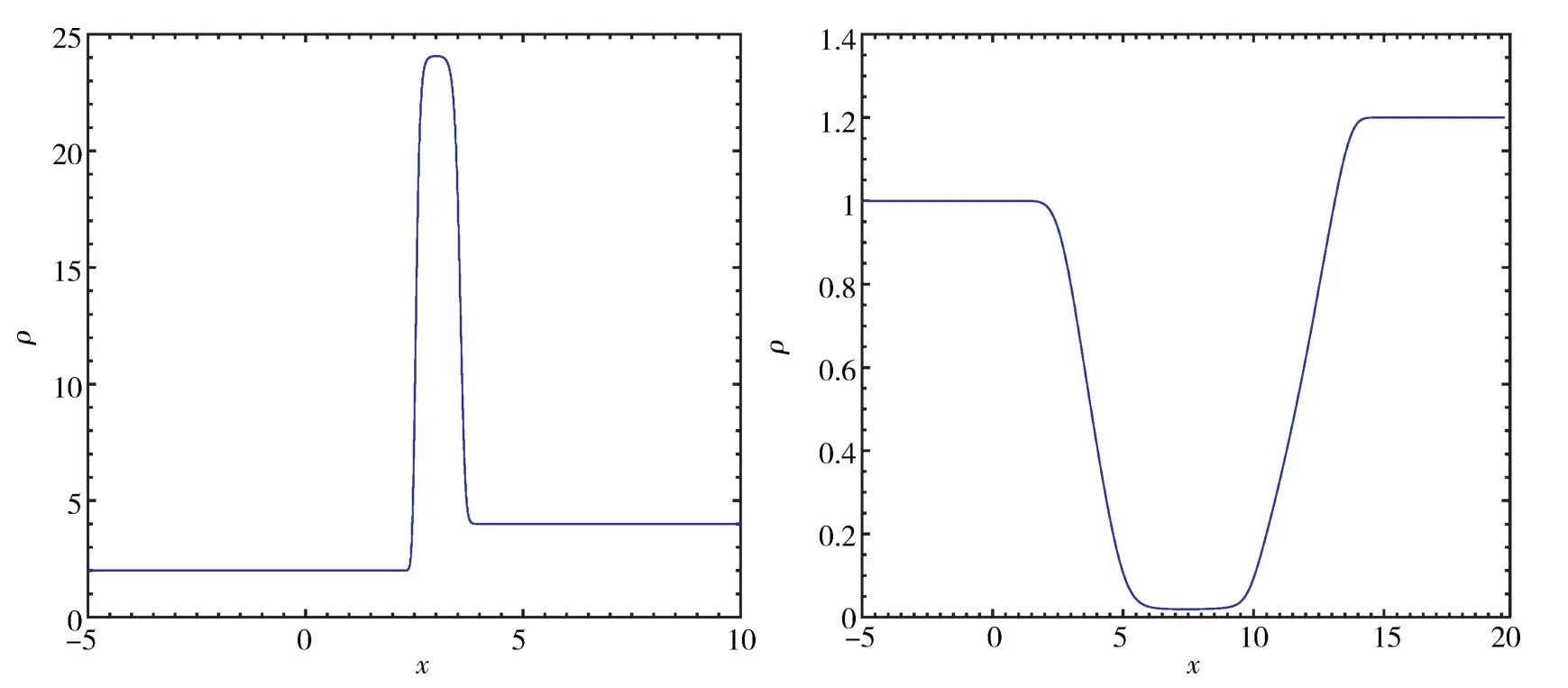
图4 ε＝0．1时δ激波（左）和真空状态（右）的密度Fig.4 Density ofδshock wave（left）and vacuum states（right）forε＝0．1