求解最小包容圆问题的一种有效算法

蔡 园， 蒋 毅， 王成露

（四川师范大学 数学科学学院 可视化计算与虚拟现实四川省重点实验室，四川 成都610066）

1 背景介绍

最小包容圆问题是求解平面上包容所有给定圆的最小的圆，该问题简写为SEC［1］.这个问题最初是由Sylvester［2］在1857年提出的，并且可以在线性时间内求解.最小包容圆问题有很多的应用背景，比如规划共享设施的位置、环境科学、模式识别、机械工程以及计算机制图等，具体参考文献［3-6］.许多文献都涉及了最小包容圆问题的算法，例如切平面法［7］、二次规划法［3］以及基于Voronoi图的算法［8］.最小包容圆问题的数学模型描述为如下形式

其中，（x，y）和R分别代表最优圆的圆心和半径，¯=｛o1，o2，…，om｝表示m个给定的圆，它们的圆心和半径分别为｛（a1，b1），（a2，b2），…，（am，bm）｝和｛r1，r2…，rm｝.根据半径的不同，最小包容圆问题又可以分为以下的2种情况：ri=0以及ri＞0，其中i=1，2，…，m.对于ri=0，已经有许多文献报道，比如文献［9-10］.本文主要研究ri＞0的情况，可参考文献［3，7，11］等.在文献［3］中，一共研究了4种著名的算法来解最小包容圆问题，包括二次规划法、次梯度法，随机增量法以及二阶锥规划法.在他们的计算实验中，表明了最好的算法是二次规划法.文献［3］中二次规划法最主要的思想就是把问题（1）转化为如下的一个含有线性约束的二次规划问题

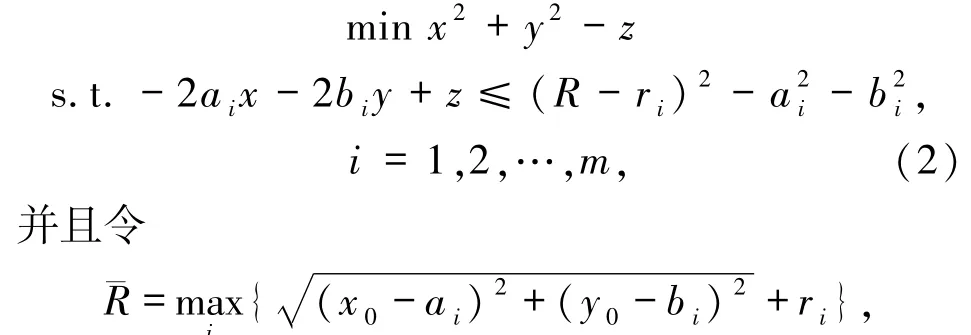
（x0，y0）为任意给定的初始值，此时问题（2）是凸优化［12］.在本文数值实验中，与文献［3］中最好的二次规划法进行比较，新算法处理的数据越大越有效.值得提出的是，本文思想来源于文献［13-14］中的方法.

2 算法描述

下面介绍本文提出的新算法.根据文献［3］中的定理2.1，知道最小包容圆问题（1）与非凸二次规划问题（2）在一些条件下是等价的.对于问题（2），是含有非凸约束的二次规划问题.引入一个新变量V来替换平方项R2，并结合文献［15-21］的有关线性松弛的研究，可以得到问题（2）的如下松弛问题

定理2.1问题（3）是问题（2）的线性松弛.

证明设（x，y，R，z）是问题（2）的一个可行解，则满足如下不等式：

根据最小包容圆问题（2）中R和¯R的定义，知道

由（5）和（7）式得，（x，y，R，z，V）（V=R2）是问题（3）的一个可行解.因此，问题（3）是问题（2）的线性松弛.

由定理2.1的证明，可以得到以下引理.

引理2.2当V=R2时，问题（3）与问题（2）是等价的.

问题（3）是含有线性约束的二次规划问题，可以有效地求解.如果V=R2，则问题（3）的最优解是问题（2）的最优解；否则，根据文献［13］中提到的切平面方法，在问题（3）中加入有效的切平面并求解新的二次规划问题.基于这种思想，给出以下求解最小包容圆问题的算法.

算法1

步骤1 初始化：k=0.给定初始点（x0，y0），并计算

再用MATLAB求解问题（9），更新k：=k+1，得到问题（9）的最优解（xk，yk，Rk，zk，Vk）.

引理2.3［3］设（x*，y*，R*）是问题（1）的一个最优解当且仅当（x*，y*，0）是问题（2）的最优解，且有R=R*时，问题（2）与问题（1）是等价的.

有关算法1中使用的割平面的研究，可参见文献［13］.根据文献［13］，可以得到（8）式是有效的切平面且算法1是收敛的.又由引理2.2和2.3，停机准则｜xk2+yk2-zk｜≤ε和｜Rk2-Vk｜≤ε是适定的.

定理2.4算法1产生的序列的极限点是问题（1）的最优解.

证明设（x*，y*，R*，z*，V*）是算法1产生的序列的极限点，则有x*2+y*2-z*=0且V*=R*2.由V*=R*2，可以得到V*-2αR*+α2≥0是成立的.因此，问题（3）与问题（2）是等价的，即（x*，y*，R*，z*，V*）是问题（2）的最优解.由引理2.2和2.3可知，（x*，y*，R*）是问题（1）的最优解.

3 数值实验

本节主要比较算法1和文献［3］中二次规划法在MATLAB中的数值表现.所有的测试数据都是随机产生的，每一组圆的产生均满足独立的正态分布N（0，16），每组圆的半径均满足均匀分布U（0，1），并且保证这些圆都是不相交的.在数值实验中，取初始值（x0，y0）=（0，0），ε为10-6.测试了不同大小的随机例子，m的范围是从18 000到30 000.对于不同的m，分别取50组随机产生的数据进行计算，再求这50组数据得到的平均值.产生的结果是在内存4 GB、2.5 GHz英特尔酷睿处理器的个人电脑中得到.数值结果概括到表1～4中.在这些表中，m代表圆的个数，k代表算法1产生的迭代次数，nA是平均迭代次数，nmax是最大迭代次数，nmin是最小迭代次数，t是平均CPU时间（单位用s表示），QP［3］表示文献［3］中的二次规划法，Delta-T表示2种算法的时间差.最终的数值结果表明算法1处理的数据越大速度比二次规划法越快.

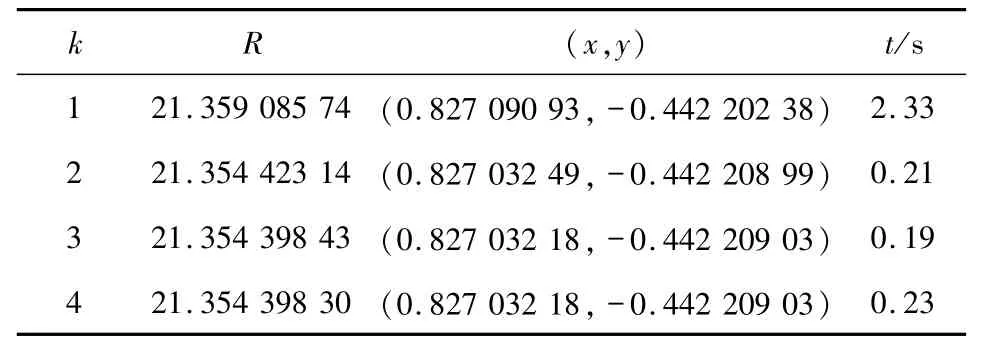
表1 m＝30 000时，算法1每次迭代的计算结果Tab.1 Computational results for 30 000 circles by the Algorithm 1

表1给出了当m=30 000时，算法1求解最小包容圆问题的迭代次数及每步迭代所用的CPU时间.值得注意的是在k=3和k=4时，圆心已经相等.

表2给出了算法1的迭代次数.已知圆的个数m是从18 000到30 000之间取了5组值，针对同一组m分别取50组随机数据所得的平均值结果.其中算法1的平均迭代次数约是4，最大迭代次数是6，最小迭代次数是3.不难发现随着已知圆的个数m的逐渐增加，算法1的迭代次数几乎没有变化.因此，可以得出算法1的迭代次数与圆的个数之间没有联系.

表2 算法1的平均迭代次数Tab.2 The number of iterations on Algorithm 1

表3给出了QP［3］与算法1求出的最优值.对于同一组m，可以看到2种算法求出的最优值是相同的.

表3 2种算法的最优目标值Tab.3 Objective function value of two methods

表4给出了QP［3］与算法1的平均CPU时间差.数据结果表明，当已知圆个数m取18 000到22 000时，算法1与QP［3］的计算时间几乎相等.但随着已知圆个数m（大于22 000）的逐渐增加，算法1的计算速度比QP［3］更快.当m=30000时，QP［3］的平均CPU时间约是算法1的1.6倍.因此，数值结果验证了算法1的有效性.

表4 2种算法的平均CPU时间Tab.4 Average running time of two methods

图1给出了m=9时，由算法1产生的最小包容圆.可以清楚地看到，算法1求出的最优圆是非常精确的.

图1 给定9个圆，由算法1产生的最小包容圆Fig.1 The smallest enclosing circle for nine circles by Algorithm 1