尺寸优化技术在大型夹具设计中的应用

崔英伟，闫旭东，路梓照

（1.北京强度环境研究所，北京 100076； 2.天津航天瑞莱科技有限公司，天津 300462）

引言

振动试验是检验产品在设计、元器件、零部件、材料等方面缺陷的必要试验。在进行振动试验时，大部分产品需要固定在夹具上，此时夹具的动力学特性将直接影响着振动试验的准确性，因此一个合理的夹具设计是十分必要的[1]。

客户公司提出的牵引变压器振动试验截距设计指标是一阶频率计算值大于100 Hz，对于一般的振动试验夹具这个指标比较好实现，但是对于本产品则十分困难。由于牵引变压器重达9.2 t，我试验室最大推力振动台仅为35 t振动台，根据试验谱型经过推力换算后留给夹具的重量不足4 t，而且试验件安装点最长边为2.8 m超出振动台台面范围，这就使得夹具与试验件的安装点全部悬在振动台台面以外，这些因素都大大的增加了夹具设计的难度。

在设备能力有限的情况下满足如此严苛的指标要求，只能从合理的夹具设计上入手。以往进行夹具设计的思路大多是先凭经验进行大体设计，然后采用有限元分析软件对设计的夹具进行模态分析，通过模态分析结果有针对性的对低频振型进行结构修改，修改方式通常仅仅是单纯的哪里薄弱就补哪里，由于没有重量要求所以往修改后的夹具重量都会急剧增加，夹具重量上很难控制，而且仅仅目的单一的“补”往往是加强了一个振型的频率，而又由于质量增加削弱了另外一个振型的频率[2]。为此，夹具设计过程中需要大量的反复设计和计算，这都大大的增加了夹具设计的时间。为了满足客户的严苛要求和紧张的设计周期我们必须采取新的设计方法加快夹具设计效率并且提高设计准确度。

ANSYS Mechanical APDL软件中的结构优化模块提供了一系列的“分析—评估—修正”的循环过程。对于初始设计进行分析，依据设计要求进行评估，然后修正设计。这一循环过程重复进行直到所有的设计要求都满足为止。应用ANSYS进行夹具尺寸优化可以大幅度的提高设计效率，将ANSYS软件中的优化程序应用到夹具设计中，成功完成了试验夹具的设计工作。

1 试验夹具初始结构设计

尺寸优化设计需要针对一个原始结构进行优化设计，这个设计流程需要制定一个初始的夹具设计方案。牵引变压器整体重量9.2 t，最长边尺寸为2.8 m，实际装机时由四个安装位置悬挂安装，牵引变压器示意图如图1所示。

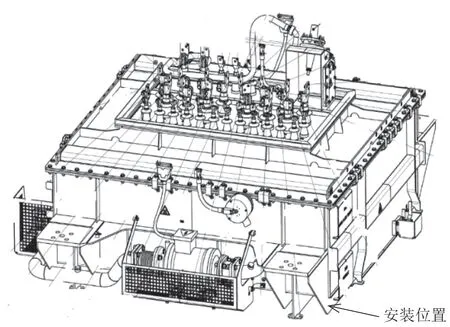
图1 牵引变压器示意

为满足牵引变压器安装要求，选取大尺寸截面梁附加立柱的形式作为夹具的基本结构形式。由于试验频率主要集中在70 Hz内的中低频，所以夹具的材料选取为钢材，加工方式为钢板焊接，简化后牵引变压器与夹具组合示意如图2所示。

图2 牵引变?压器与夹具组合示意

现有35T推力振动台拓展台面为2.5 m*2.5 m，夹具尺寸超出台面外，夹具与振动台组装示意如图3。

图3 试验夹具与振动台组装示意

2 优化尺寸选取

根据模态分析理论可知：

多自由度体系在振动激励下的运动方程为[3]：

式 中：

[M]，[C]和[K]—分别为结构的质量，阻尼和刚度矩阵；{u}—质点位移，是时间T的函数；—加速度时程。

当外力为零时并且阻尼为零的条件下可得动力方程：

在非零初始条件下求解此自由振动方程可以得到反应结构本身固有特性的自由振动频率和振型。

求解结构动力特性的数值计算方法很多，通常有分块（Lanczos）法，子空间法（SubPlace）、兰索斯法 （Bloeklanezos）、缩减法（Reduced）、动力学方法（PowerDynamies）和里兹向量法（Ritz）等。本文选取基于PCG算法的分块Lanczos方法进行夹具模态分析。

上文可知，影响结构模态特性的主要因素有两个，一个是质量矩阵{M}，一个是刚度矩阵{K}。在结构基本形式确定后，只需找出影响结构重量和强度的关键尺寸，对这些关键尺寸进行优化，则可以快速计算出合理的夹具尺寸。对于这种梁柱结构形式来说，这些关键尺寸包括：梁的截面尺寸、柱的高度、肋板厚度等。优化限制参数为夹具的重量不超过4T。优化目标为尽可能的提高结构的一阶固有频率。ANSYS软件中可以提供不超过60个设计变量[4]，所以在不确定结构关键尺寸时可以适当的多选需要优化的尺寸，凭借工程经验，选取影响结构强度的尺寸如图4所示。图中X1~X4以及梁的宽度T为需要优化的结构尺寸。由于夹具选用钢板焊接结构，钢板厚度的选取同样成为制约结构特性和重量的关键，故同时选取外部钢板厚度t1及内部肋板厚度t2进行优化。

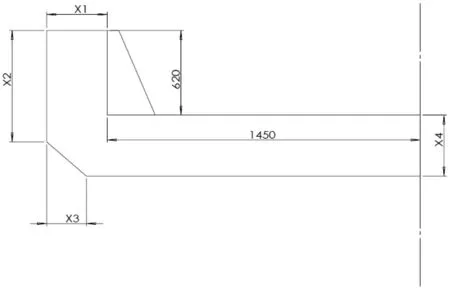
图4 结构优化尺寸示意图

3 应用ANSYS进行尺寸优化

3.1 参数化建模

在进行优化前必须设定一个优化的初始值，初始值通常凭借工程经验确定，初始值的确定应基本合理，不应设置初始尺寸过于薄弱或过于健壮，使得初始强度过低或者质量过大，造成数值计算出现错误。模型建立必须通过ANSYS的APDL语言进行参数化建模[5]，对设定的关键尺寸进行参数化设定，设定初始值的APDL命令如表1 。

表1 优化目标的参数化设置

夹具模型选取单元为shell63单元，为了加快运算速度，将试验件简化成为质量节点，通过节点耦合CP命令进行自由度耦合。模型底部约束方式为底梁上下表面固定约束，约束范围与实际安装范围相符，具体模型如图5所示。

图5 夹具参数化建模模型图

3.2 求解并提取参数

对模型进行模态分析，得到模型的一阶固有频率为79 Hz，此时模型的重量为3.91 t，振型为Z向左右摆动，一阶振型如图6所示。从初始计算结果可知，虽然夹具质量符合要求但是结构一阶频率远低于客户要求，需要进行优化。

图6 夹具一阶振型

提取一阶固有频率（变量名为F），提取质量（变量名WT）。优化分析的设计变量为上文选出的最可能影响结构一阶固有频率的关键尺寸。状态变量是限制变量，选取夹具重量（WT）作为状态变量，限制范围是小于4T。在优化分析中所有的目标函数都是向小值优化，为了实现尽可能的提高一阶固有频率，引入FF=1/F变量，以FF作为目标函数进行优化。具体的参数设定及DV优化范围如表2 。

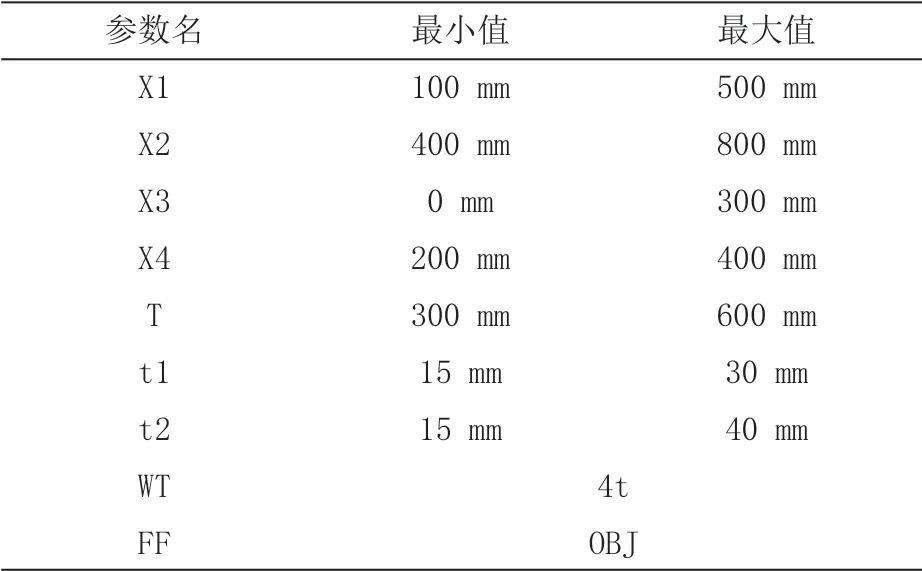
表2 优化范围

3.3 指定优化算法

ANSYS中的优化方法提供了零阶方法、一阶方法、随机搜索法、等步长搜索法、乘子计算法和最优梯度法。

综合计算成本和优化精度的考虑选择零阶方法进行优化。零阶方法之所以称为零阶方法是由于它只用到因变量而不用到它的偏导数。在零阶方法中有两个重要的概念：目标函数和状态变量的逼近方法，由约束的优化问题转换为非约束的优化问题。

零阶方法中，优化程序用曲线拟合来建立目标函数和设计变量之间的关系。这是通过用几个设计变量序列计算目标函数然后求得各数据点间最小平方实现的。该结果曲线(或平面)叫做逼近。每次优化循环生成一个新的数据点，目标函数就完成一次更新。实际上是逼近被求解最小值而并非目标函数。

3.4 进行运算并分析结果

设置优化迭代次数为40次，优化至18步时运算收敛，产生最优计算结果如表3所示。

表3 各尺寸的优化结果

优化后一阶固有频率为111.78 Hz，阵型为X向前后摆动，优化后得到模型及一阶振型图如图7所示。

图7 优化后一阶振型