机械式振动台结构设计及其波形复现性能测试研究
郭迎庆,李宗荫,2,杨晓璐
(1.南京林业大学机械电子工程学院,江苏南京 210037;2.中国电子科技集团公司第十六研究所,安徽合肥 230601)
0 引言
随着航空航天、电子工业的快速发展,各种用于测试航天器部件等仪器设备的振动试验装置也日益发展起来。由于航天及电子产品在设计阶段以及验收阶段均需要进行一系列的环境振动测试,这就要求相应的测试设备具有较高的检测性能[1-4]。振动台作为一种集结构激振、性能测试和数据分析等功能为一体的科学振动试验装置,已经被广泛地应用在航空航天、车辆交通、建筑结构和工业自动化等众多工程领域[5-6]。伴随着振动台相关理论研究的深入和技术的发展,各种试验结构模型也逐渐趋于精简化、智能化[7],从而导致中小型振动台在研究中的地位逐渐提高。但是,当前市面上现有的地震模拟振动台多为液压驱动的大功率振动台,其存在污染严重、建造代价高昂等弊端,而现有的电机驱动的中小型振动台却存在普遍进口、价格昂贵、开放性低等缺点。因此,如何设计一款拥有自主知识产权的结构精巧、性价比高的中小型振动台试验装置,对于降低振动测试成本、提高测试性能具有重要的工程实际意义。
国内外相关领域的研究人员已经进行了多年的振动台试验研究,并已经将相关研究成果应用到实际工程当中。王猛等[8]提出一种偏心轮式机械振动台,并通过有限元分析验证了所设计振动台的可行性。田军委等[9]在活塞式发动机工作原理的基础上提出一种对称式曲柄滑块振动台方案,利用其对称式的特点有效抵消高频振动时的惯性冲击。谢维泰等[10]采用机械运动机构中常见的曲柄连杆机构设计了一种机械式超低频振动台,并且通过典型应用实例验证了机械式超低频振动台的实用性。在各类振动台中,大推力液压式振动台的技术相对较为成熟,而小型机械式振动台研究较少,其中电动振动台因其承载范围广、工作频段宽、波形好、易控制等诸多优点而备受青睐,成为一种应用广泛的振动台装置[11-13]。由于机械式振动台在某些振动试验下有着独特的优势,所以针对机械式振动台的相关技术研究具有重要的工程实用价值。
综上,本文基于实际振动测试工程需要,结合计算机技术、嵌入式控制技术和电机控制技术,自主研制一套能精确再现加速度激励测试信号的振动台系统。利用系列性能测试试验对设计的振动台进行性能考核,经过测试表明振动台波形复现精度较高,具有很好的波形跟随性,满足实际工程需要,可为后期中小型高精度振动台的研究和设计提供一定的参考意义。
1 振动台系统架构
双向单自由度小型振动台试验装置整体系统架构组成框图如图1 所示,主要包括控制模块、激励模块、试验模块和数据采集模块。其中,控制模块由PC 机与嵌入式控制器组成,实现对激励模块的电机控制信号输出;激励模块由伺服电机及其驱动器组成,实现对试验模块的激励输出;试验模块由丝杆、台面等机械结构组成,实现试验结构的固定及对激励模块输出的响应;数据采集模块由位移传感器、加速度传感器及编码器组成,实现局部闭环控制及振动台信号采集。此系统架构在满足性能指标的同时,大大缩减了研制时间和试验成本。
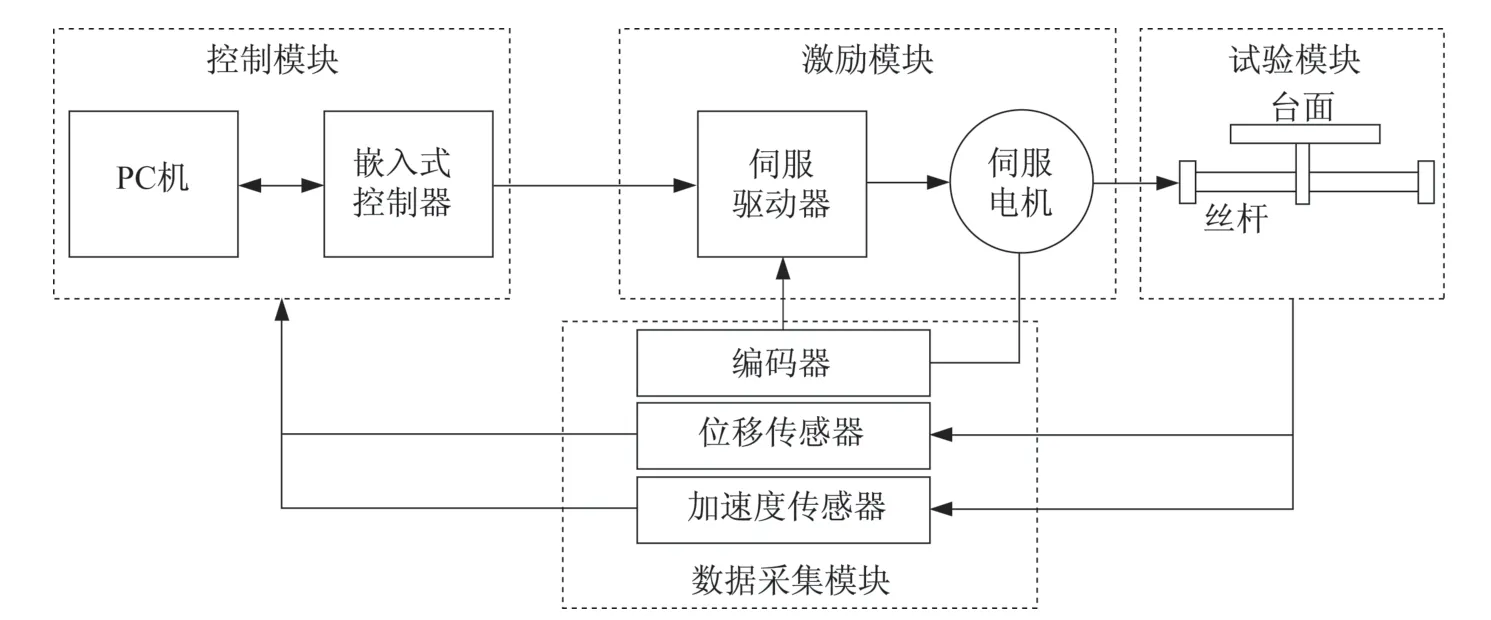
图1 振动台试验装置整体系统架构框图Fig.1 Block diagram of the overall system architecture of the shaking table test device
2 关键模块设计
为了实现振动台对不同原始波形的精确再现,完成对待测设备的振动测试试验,需要设计的振动台试验装置中各个模块彼此之间协调工作,因此,振动台系统中关键模块的设计是否合理显得尤为重要。
2.1 原始数据处理
当前振动台试验测试激励信号大多数以加速度信号形式存储[14-16],并且选用电动伺服系统作为振动台的激振源,为了提高控制精度需要在电机运转的过程中对其速度和位移有严格的控制,综合考虑采用伺服控制模式中的位置控制来完成系统力的转换。
因此,需要求解出试验输入波形的位移和速度时程曲线,并通过这两条曲线计算出伺服电机每次动作所需的控制信号,故加速度信号的积分处理成了振动台试验中不可或缺的一环。
选择LabVIEW 作为数据处理平台[17-18],采用模块化方式按层次将程序分解成多个子VI,由顶层VI 模块在高层管理并调度各子模块工作,从而实现数据的读取、处理、显示和保存等功能。同时,子VI的代码和数据会保留在内存中,有效降低了程序运行时的内存占用量。主模块具体设计的程序面板如图2 所示。其中,V1 为数据读取模块,选择数据通信中“队列操作”,结合条件结构中while 循环保证数据读取的持续性;V2 为数据处理模块,采用“元素出列”处理和双精度转换完成数据格式的处理,然后在频域范围内进行数据的解析,并且在解析过程中进行数组必要元素取舍,保证数据转换的精度;V3 为数据显示模块,显示经处理后的输出脉冲数、速度和方向数据。
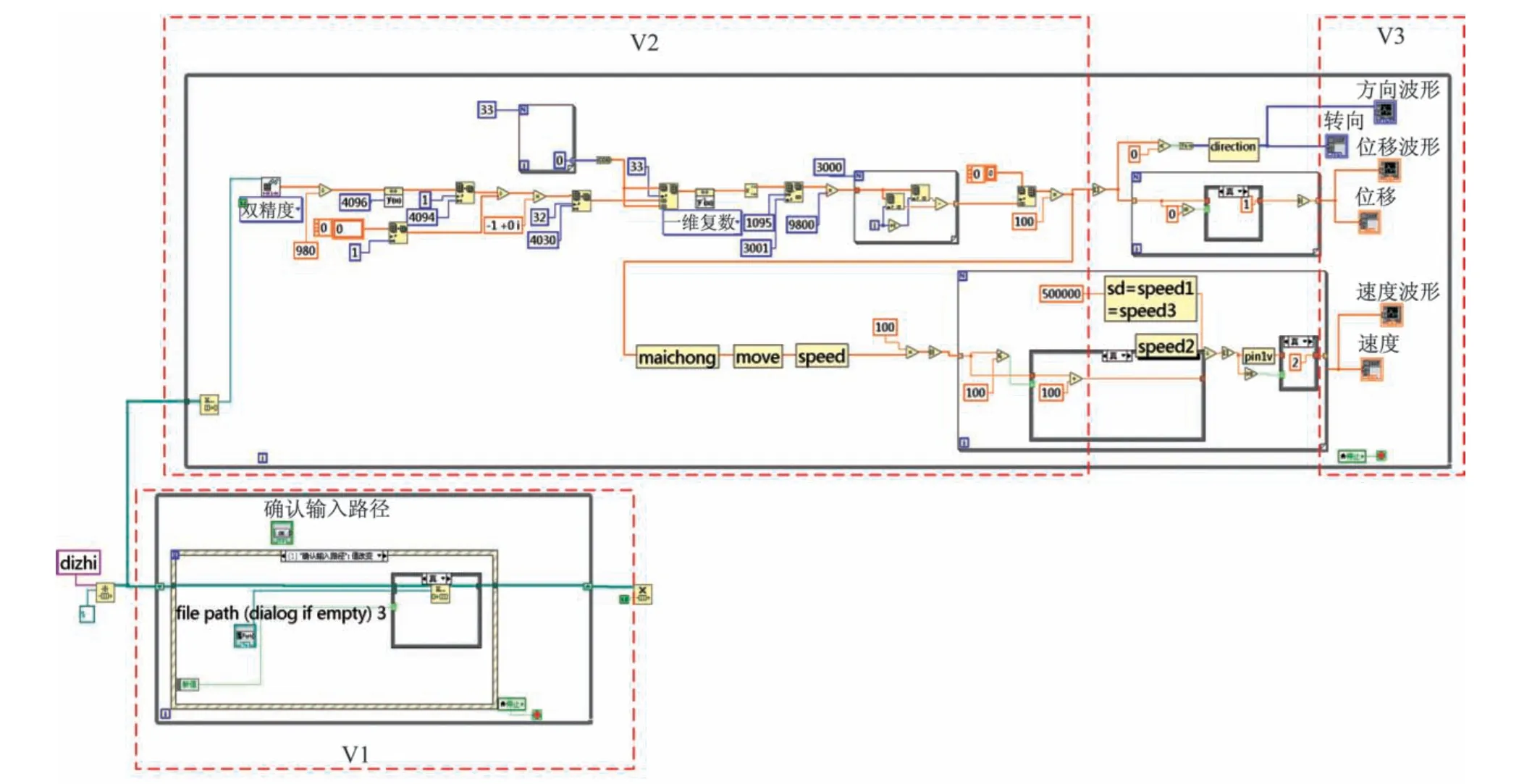
图2 主模块控制程序面板Fig.2 Main module control program panel
以220 gal 的Artificial 加速度地震波为输入信号,处理后保存的速度与位移信号如图3 所示。
2.2 机械结构和控制器的设计
合理完整振动台机械结构和软硬件的设计是振动台控制系统正常运行的保障。根据振动台性能指标完成对振动台整体机械结构的设计,同时根据振动台系统的控制要求并且遵循实用化、模块化的方式,以嵌入式控制芯片为核心完成振动台控制器的设计。控制器和机械结构两者之间相互联系、协调工作,保障振动台系统的正常运行,其具体构造简图如图4 所示。
2.2.1 机械结构
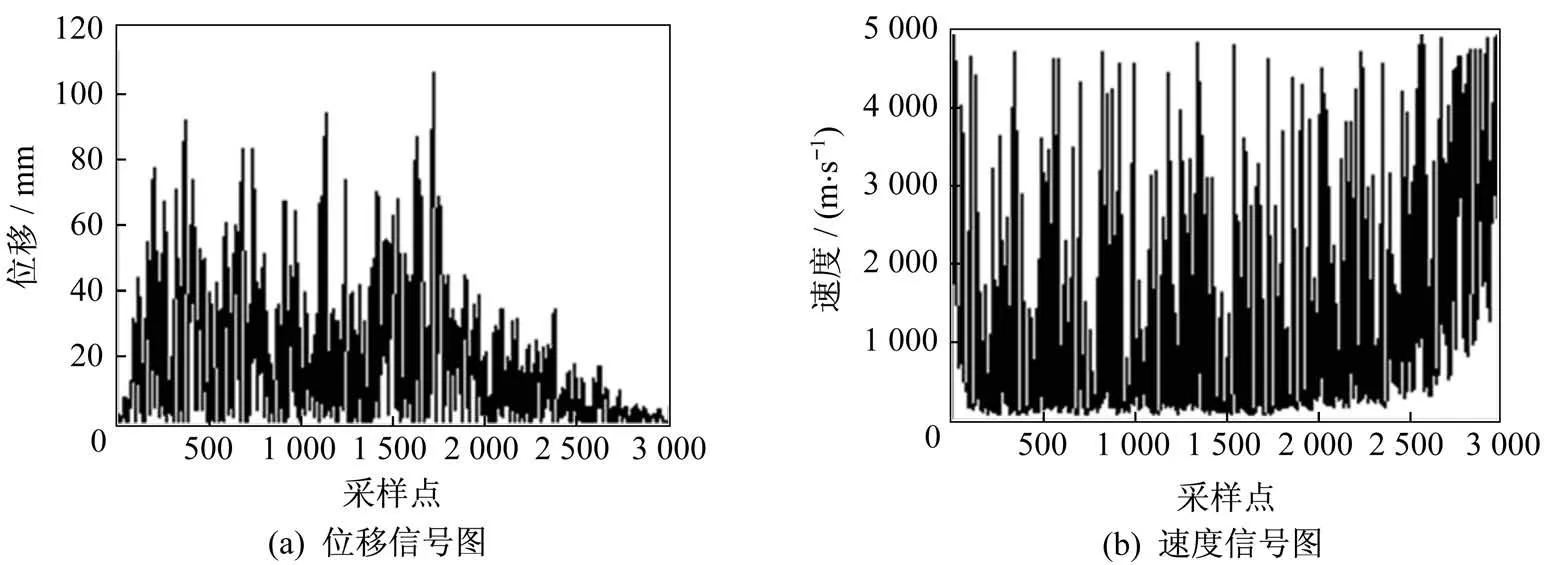
图3 基于LabVIEW 处理后的数据信号图Fig.3 Data signal diagram processed based on LabVIEW
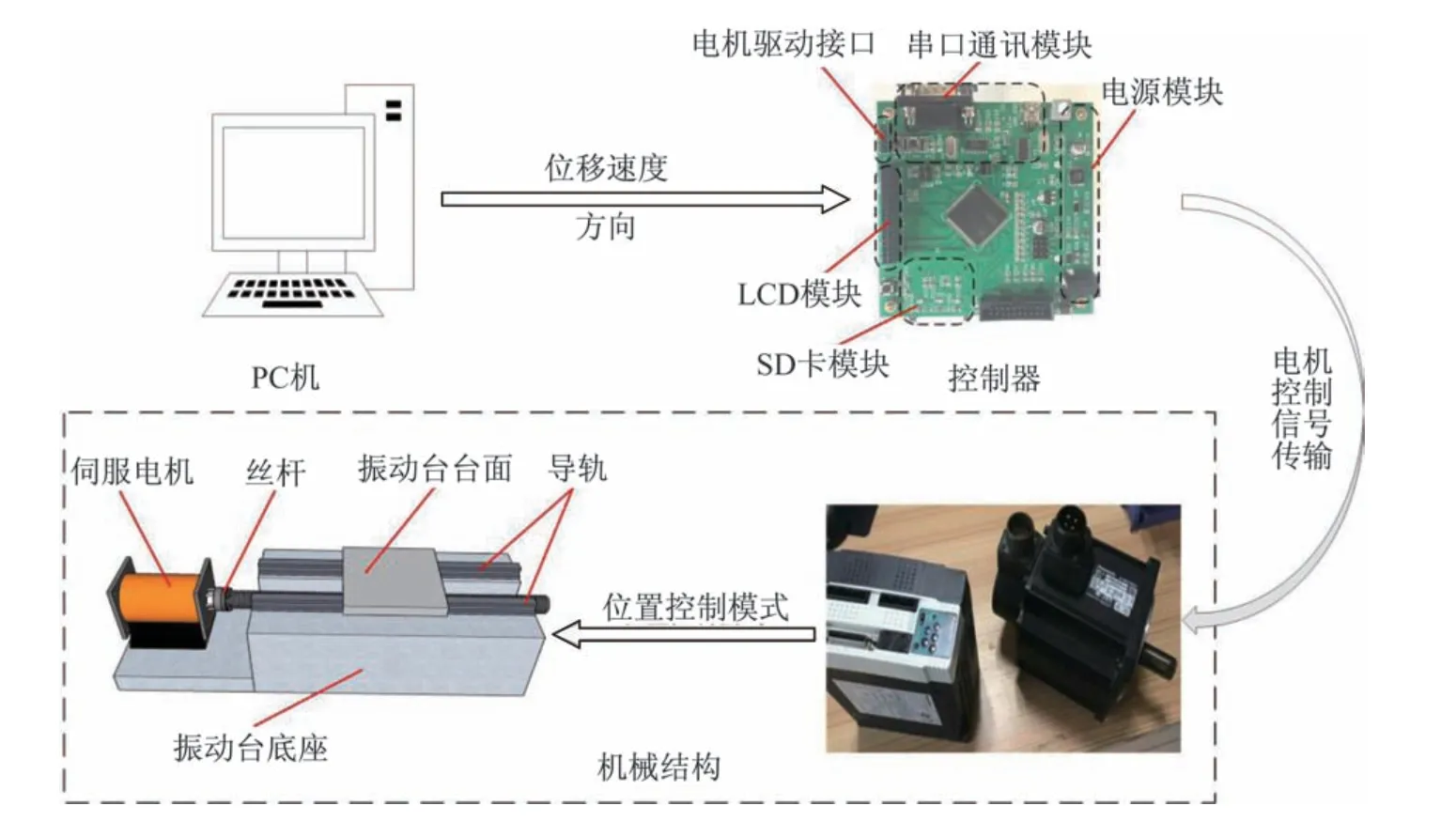
图4 振动台结构简图Fig.4 Vibration table structure diagram
根据实际设计要求,确定振动台尺寸,其主要组成部分尺寸见表1。以伺服电机及其驱动器为激励源,将丝杆与伺服电机的电机轴固接,使伺服电机的转动转换成平动,同时将丝杆螺纹与振动台面螺纹对接,实现对振动台面及其上的试验结构的激励,完成动力的流畅传递和试验结构的加载。此外,伺服电机的驱动器选用位置控制模式并结合下位机控制器实现伺服电机准确运转,并且根据振动台实际试验要求,在振动台台面及其上的试验结构进行包括位移、力、加速度在内的多种数据采集,以便后期对试验结构进行性能分析。
2.2.2 控制器
选用以STM32 为基础的嵌入式最小系统,搭载振动台控制系统所需功能要求所设计的一系列外围电路。将电机控制状态通过串口及时反馈给上位PC 机,构建上位PC 机与被控对象之间的数据通信,完成对上位PC 机数据的接收和SD 卡中文件数据的读取,并将所读取的数据转换成对伺服电机的精确PWM(Pulse Width Modulation)控制信号输出,从而完成对振动台控制系统的控制任务。

表1 振动台装置尺寸Tab.1 Dimensions of shaking table apparatus mm
基于位置控制模式下,控制器与机械结构之间的数据转换原理如图5 所示。控制器向驱动器发送脉冲位置指令,脉冲位置经驱动器控制电机转动,电机带动编码器转动,编码器将采集到的角位移信号处理后得到的反馈脉冲数送至驱动器,从而形成局部位置闭环控制,同时电机转动带动丝杆以一定速度旋转,经齿轮后作用于振动台台面,此时丝杆的实际位移量M的表达式为
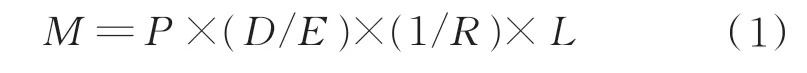
式中:P为控制丝杆移动位置的脉冲数量;D为指令分倍频比;E为编码器反馈脉冲数;R为减速比;L为丝杆螺距。
此时,与该脉冲频率所对应的电机转动速度V1和丝杆实际转动速度V2分别表示为
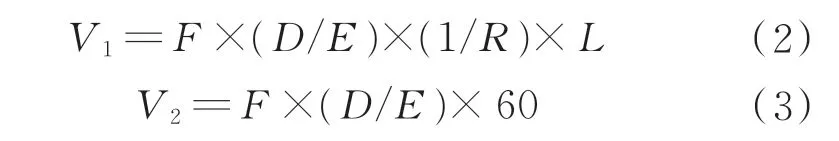
式中:F为控制电机移动速度的脉冲频率。
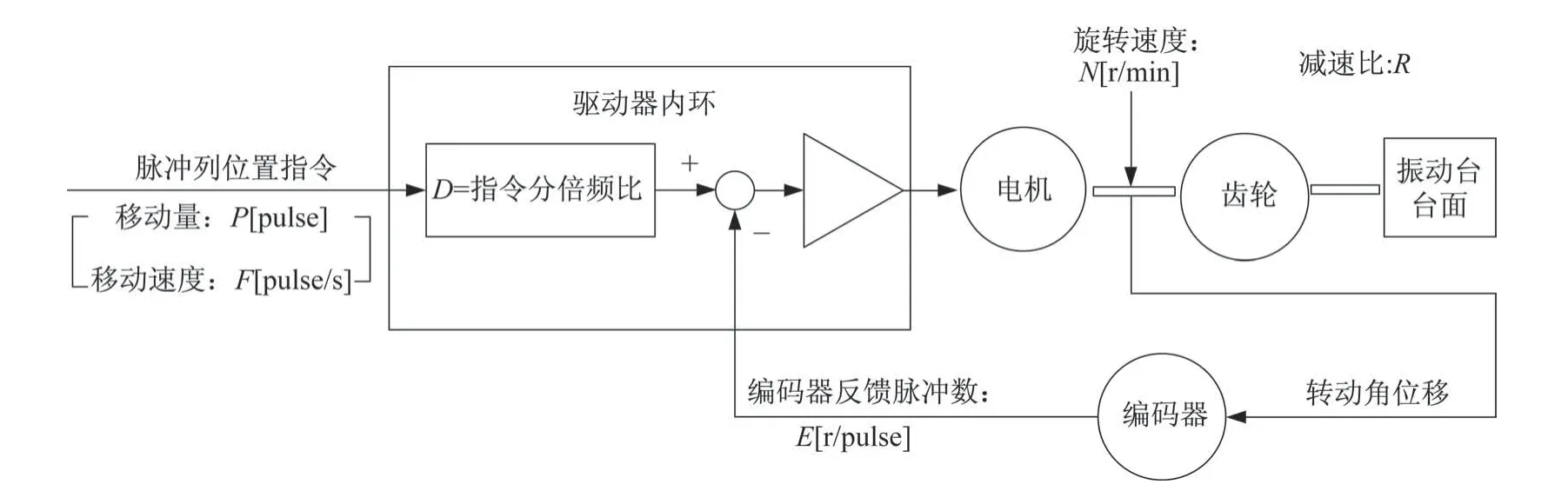
图5 位置控制模式下信号转换原理图Fig.5 Schematic diagram of signal conversion in position control mode
3 振动台性能分析试验
基于振动台的试验要求,完成各个模块的设计,搭建完整的振动台试验系统,其具体试验装置如图6所示。为了验证振动台的波形复现能力,以真实的地震波加速度信号为试验测试加载信号,针对振动台控制系统各个关键环节进行性能分析试验。

图6 振动台试验系统实物图Fig.6 Physical image of shaking table test system
3.1 系统硬件性能试验
振动台控制系统是整个振动台系统的核心,系统硬件的性能是整个系统是否稳定可靠的关键因素之一。为了验证振动台系统硬件的稳定性和准确性,设计如下试验:截取一段振动台控制模块处理后的电机控制信号作为下位机控制器的输入,其具体数据片段见表2。下位机控制器根据输入完成对SD 卡的文件检索及数据读取功能,整个数据读取过程耗时在1 s 以内,满足振动台控制的要求。同时,控制器对输入数据进行处理分析运算出与电机控制相关的位置、方向和速度信号,并通过LCD 显示具体数值,将读取结果(如图7 所示)的显示数据与测试数据进行对比发现完全一致,验证了串口通讯的稳定性和SD 卡读取的准确性。
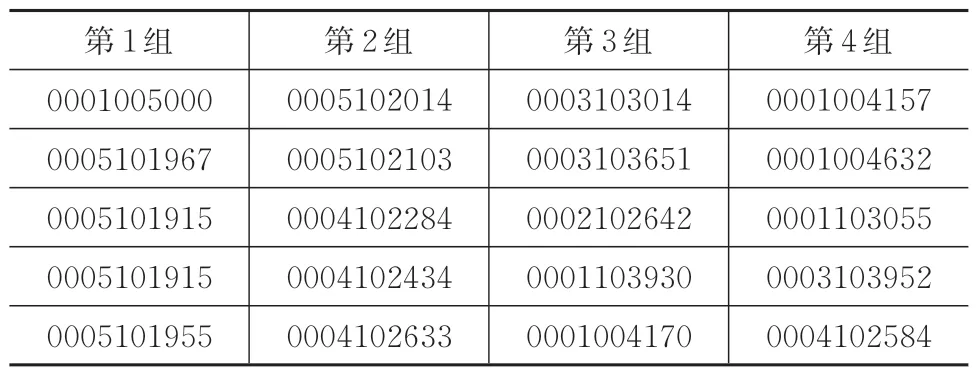
表2 系统硬件性能测试数据Tab.2 Performance test data of system hardware
3.2 伺服电机控制试验
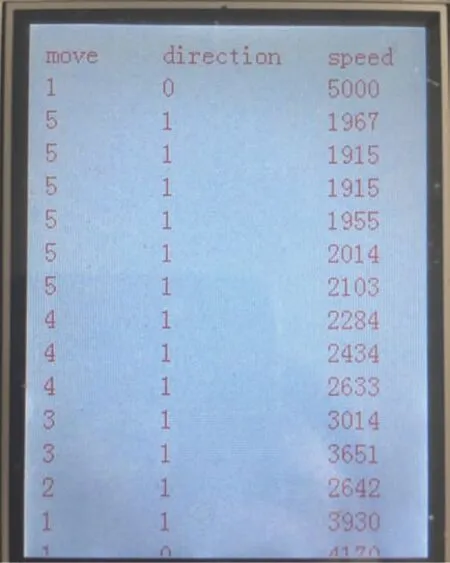
图7 测试数据LCD 显示结果Fig.7 Test data LCD display results
伺服电机的控制效果直接影响到整个振动台控制系统的控制精度,对伺服电机的精确控制,是系统正常运行的保障,也是最为重要的一环。综合考虑主控芯片控制能力,拟采用位置控制模式作为控制器对于伺服电机的主要控制思路。为验证位置控制精确性,设计如下试验:通过上位机向下位机控制器发送连续位移阶跃的电机控制信号,以5 mm 作为阶跃幅值,利用位移传感器实现对振动台面位置信号的采集。试验结果如图8 所示,最大误差为2%,考虑到位移传感器采集的一定误差,采用伺服电机位置控制时,控制精确很高,其控制精度可达0.1 mm,足以胜任振动台位置控制精度要求。
3.3 空载振动台面波形复现试验
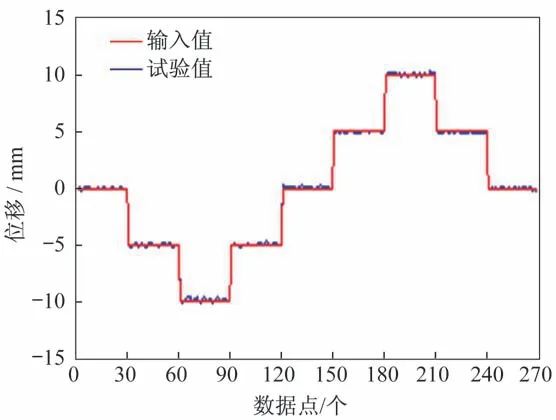
图8 位置控制阶跃输入试验结果Fig.8 Step input test results of position control
完成了振动台试验系统各个关键环节的有效性和可靠性验证,从试验的角度证实了本文所设计的振动台控制系统的可行性。在此基础上,以400 gal的真实Taft 地震波加速度信号作为振动台输入激励,采用高精度加速度传感器完成对振动台面实时加速度数据的采集,试验结果如图9 所示,试验曲线与理论的输入曲线基本吻合。输入值峰值加速度为400 gal,出现在3.7 s 处,试验值峰值加速度为388 gal,出现在3.68 s 处,峰值加速度同样很好再现。输入值与试验值最大误差出现在7.54 s 处,为68 gal,最大误差为27.3%。在试验过程中,加速度试验值呈现良好的跟随性,加速度再现结果基本满足要求。同时考虑试验过程中的试验误差以及硬件性能等因素,误差在允许的范围内。本试验验证了所设计的振动台系统在波形复现时的可行性与可靠性。
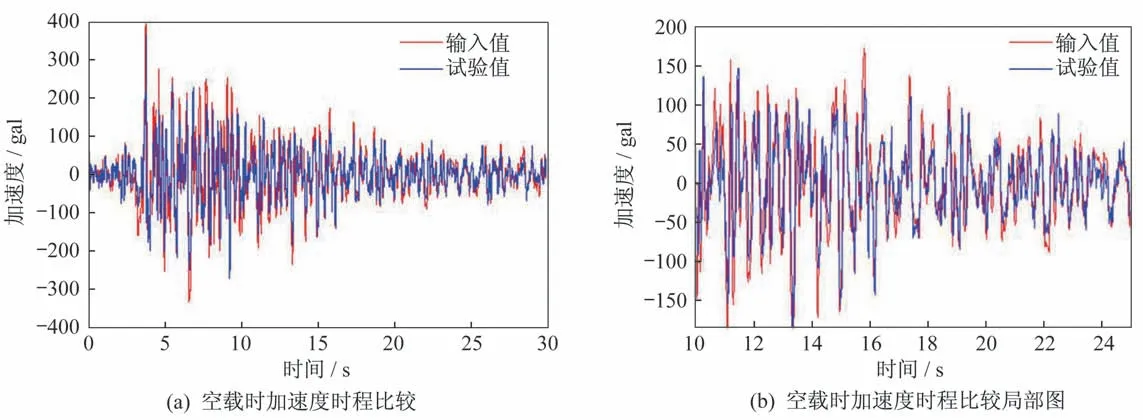
图9 Taft 波作用下空载时振动台的输入值和试验值的结果对比图Fig.9 Comparison of results between the input value and test value of the shaker table under no load Taft wave
3.4 负载振动台面波形复现试验
基于振动台在空载时良好的波形复现性能,为了检验振动台在实际负载试验情况下波形的复现精度,采用质量为93.77 kg 的Q235 型三层钢板结构作为试验负载,其负载实物如图10 所示。此次负载试验仍然沿用400 gal 的Taft 波作为振动台的激励,以便进行横向对比分析,其试验结果如图11所示。根据振动台面所测得加速度与试验输入值400 gal 的Taft 波之间的对比图可知,试验值最大峰值出现在3.68 s 处,为380 gal,而输入值出现在3.70 s 处,其值为400 gal。同时,两曲线最大误差出现于4.20 s 处,其值为69 gal,最大误差27.3%,试验值呈现很好的跟随性及还原性,负载时振动台的波形复现精度基本符合工程要求。为了进一步对比振动台在空载和负载状态下波形复现状态,当采用相同的400 gal的Taft 波作为激励加载时,台面加速度试验值之间的对比如图12 所示。

图10 振动台负载波形复现试验Fig.10 Reproduction test of shaking table load waveform
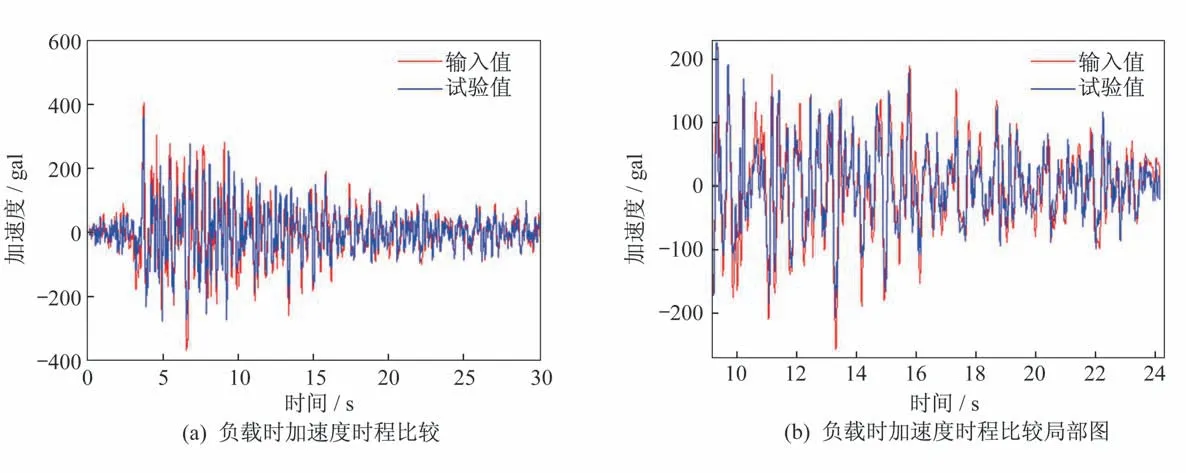
图11 Taft 波作用下负载时振动台的输入值和试验值结果对比图Fig.11 Comparison of results between the input value and test value of the shaker under load Taft wave
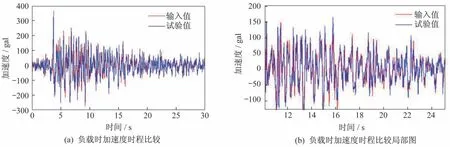
图12 Taft 波作用下负载与空载试验值结果对比图Fig.12 Comparison of the results between load and no-load test under Taft wave
根据对比图可知:在两种工况下峰值加速度都出现在3.68 s 处,峰值相差15 gal,空载情况下稍大;最大误差出现在15.80 s 处,为21 gal,最大误差为14.8%,但是总体上空载和负载状态下加速度试验值基本呈现吻合状态,具有很好的同步性。由于因负载变化而导致控制精度的变化在工程试验的允许范围之内,所以设计的振动台符合大多数工程振动测试试验要求。
4 结束语
本文以电动伺服系统为激振源,结合计算机控制技术和嵌入式控制技术,研制了一套完全自主知识产权的振动台系统,并对研制的振动台进行了关键性能测试。对系统的通讯和SD 卡文件数据读取进行测试,验证了数据通讯的准确性和快速性;在位置控制模式下对伺服电机控制效果进行测试,验证了采用位置控制模式的伺服电机控制思路的可行性;以真实激励信号作为输入,对振动台在空载和负载不同工况下波形复现精度进行测试,验证了整个系统波形复现良好,表明了设计的科学性和适用性,并且两种不同工况下波形复现误差较小,进一步验证了振动台系统的稳定性。针对振动台试验误差来源进行分析,空载时的试验误差主要来源于硬件结构连接之间的摩擦能量损耗、检测设备存在的信号干扰和振动台面高速运动时的惯性干扰等系统误差;负载时的试验误差还可能包括负载的固定情况及其试验中的振动造成的影响。为此,在后期深入研究过程中考虑引入迭代学习等智能控制策略,以完善振动台控制系统,进一步提高振动台波形复现精度。总之,本文设计的中小型振动台系统具有结构精巧、性价比高、控制精度高等优点,在实际振动台应用领域具有较高的推广价值,并且为未来中小型振动台研究提供一定的技术支持和借鉴意义。

