从数学抽象的角度审视相似形概念的教学
韩诗贵


摘 要:数学概念是抽象的,概念教学是数学教学的基石,在概念教学中发展学生的数学抽象素养是概念学习的需要,也是数学学习的需要. 文章结合相似形概念的教学,从概念的弱抽象、强抽象,以及抽象的形式化、具体化等角度进行剖析,尝试理清数学概念形成中的不同抽象形式及过程,以期在概念教学中发展学生的数学抽象素养.
关键词:相似形;弱抽象;强抽象;形式化;具体化
在《普通高中数学课程标准(2017年版)》中,数学抽象位于六大数学学科核心素养之首,是数学学习需要具备的关键能力之一. 数学抽象是数学的基本思想,反映了数学的本质特征,是形成理性思维的重要基础,贯穿于数学知识产生、发展、应用的整个过程.
众所周知,数学概念是抽象的,是抽取出事物的本质属性,舍弃其非本质属性,使人们的认识从感性的具体进入理性的抽象. 如何在概念教学中发展学生的数学抽象素养?章建跃教授认为,要选取学生熟悉的典型事例,提供丰富的材料,让学生经历完整的数学抽象过程,熟悉数学抽象的“基本套路”,在概念学习中学会数学抽象. 在概念教学中发展学生的数学抽象是概念学习的需要,也是数学学习的需要. 笔者结合苏科版《义务教育教科书·数学》九年级下册“6.3 相似图形”一课的设计与实施片断,谈一谈对培养学生数学抽象思维能力的实践与思考.
一、教学片断简述
教学片断1:相似形概念的教学.
问题1:教师手中的这两块三角板有什么共同特征?(均是含有45°角的三角板,一块是教师教学用的大三角板,一块是学生作图用的小三角板.)
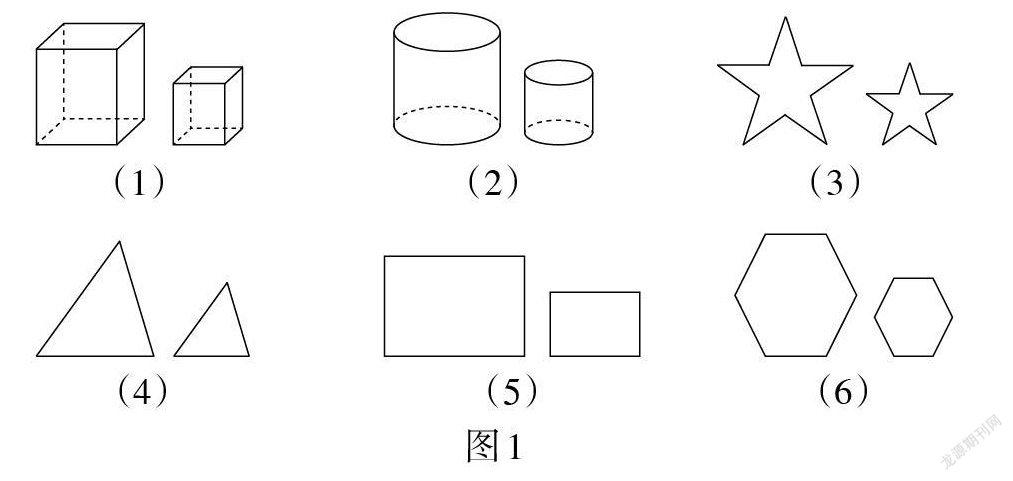
问题2:图1中各组图形有什么共同特征?
【说明】在新课导入时,选取学生熟悉的三角板等生活中常见的物品,长方体、圆柱体等常见的立体图形,以及五角星、三角形等常见的平面图形,创设有利于学生积极思考的情境,提出指向数学本质的问题. 让学生观察具有典型特征的图例,经历抽象概括的思维过程,提炼相似形的概念.
教学片断2:相似多边形概念的教学.
(1)引发认知冲突,促进思考.
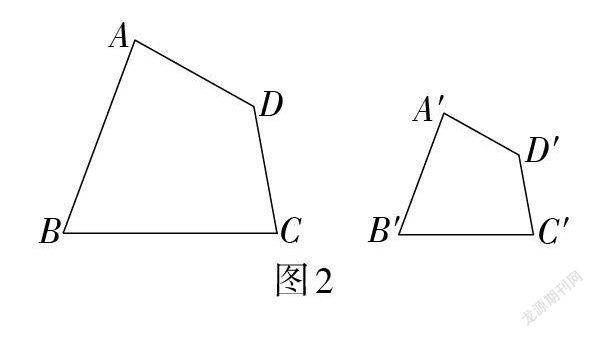
问题3:如图2,四边形ABCD与四边形[A′B′C′D′]相似吗?
师:在几何画板软件中对应调整点B和点[B′]的位置后,四边形ABCD与四边形[A′B′C′D′]还相似吗?
【说明】前一环节设置了相似的辨别练习,进一步巩固从“形”的角度理解概念. 然后通过图形的变化引起认知冲突,实现从“形”到“数”的角度研究相似多边形概念的自然过渡. 同时,认知冲突也在一定程度上激发了学生的探究欲望,以及钻研的积极性.
(2)列举反例,辨析概念.
师:仅根据“形状相同”常常难以判断两个多边形是否相似. 若要进行准确的判断,你觉得需要哪些条件?
师:首先,这两个多边形边数应该相同,对吗?
学生表示认同.
师:边数相同的两个多边形具备怎样的条件就会相似呢?
生1:各角分别相等,两个多边形相似.
生2:各边成比例,两个多边形相似.
生3:只有角相等的两个多边形不一定相似.
师:为什么?
生3:一个正方形,一个矩形,它们的四个角都是90°,但它们不相似.
师:非常好!这个反例十分典型,一个正方形和一个矩形满足四个角分别相等,但这样的两个四边形不一定相似. 那么,各边成比例,两个多边形是不是就一定相似呢?
生4:不一定相似. 正方形和菱形的各边成比例,但是不相似.
师:说说你的理由.
生4:可以设正方形的边长为a,菱形的边长为b,则正方形的四条边与菱形的四条边的比都是[ab.]
师:显然,正方形和菱形不相似. 可见,仅有各边对应成比例的两个多边形也不一定相似. 在数学上,我们这样定义相似多边形:各角分别相等,各边成比例的两个多边形,它们的形状相同,称为相似多边形.
【说明】学习本节知识之前,学生已经经历了三角形和四边形的学习,对从边和角的元素研究图形有深刻的体会,能自然联想到从边和角两个方面定义相似多边形. 而学习两个三角形全等的判定时,只需要边和角的部分元素,在这样的知识储备下,学生可能会认为各边成比例或各角分别相等就能确定两个多边形相似. 举反例有助于学生总结相似多边形的概念,理解概念的抽象定义.
(3)證明相似,理解概念.
师:在图2中,当四边形ABCD与四边形[A′B′C′D′]相似时,记作四边形ABCD ∽ 四边形[A′B′C′D′.] 同理,若△ABC与[△A′B′C′]的三个角分别相等,且三边成比例,则△ABC与[△A′B′C′]相似,记作△ABC ∽ [△A′B′C′.] 试根据相似形的定义画两个相似的三角形,并说明理由. 画好之后,先在小组内交流,然后全班展示.
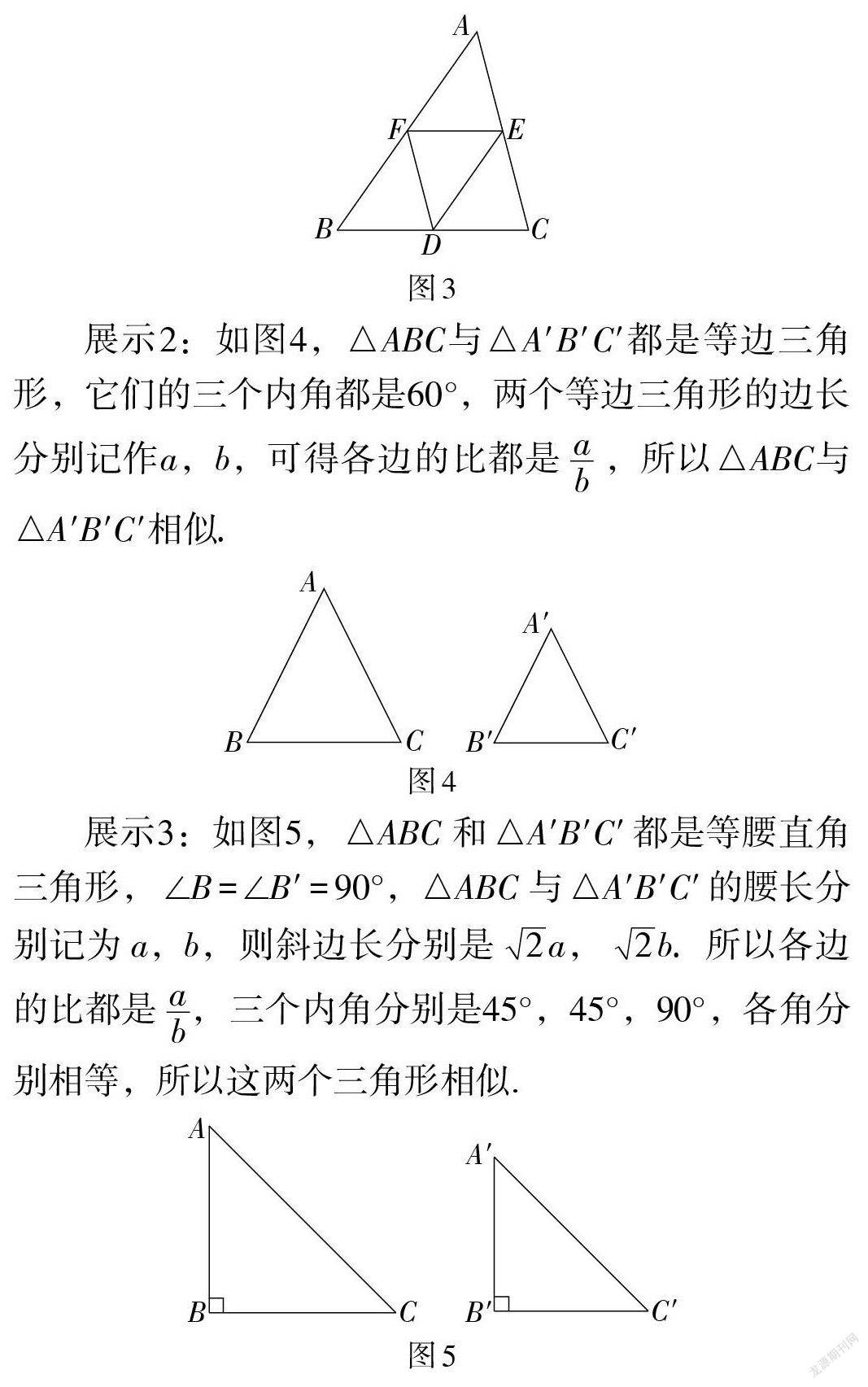
展示1:如图3,在△ABC中,分别取各边中点D,E,F,构成△DEF,根据三角形中位线的性质,可以得到△DEF和△ABC各边的比都是[12.] 又可以证得四边形BDEF、四边形CDFE、四边形AEDF均为平行四边形. 所以△DEF和△ABC的各角分别相等. 所以△DEF和△ABC相似.
展示2:如图4,△ABC与△A′B′C′都是等边三角形,它们的三个内角都是60°,两个等边三角形的边长分别记作a,b,可得各边的比都是[ab],所以△ABC与△A′B′C′相似.
展示3:如图5,[△ABC]和[△A′B′C′]都是等腰直角三角形,[∠B=∠B′=90°,△ABC]与[△A′B′C′]的腰长分别记为[a,b,] 则斜边长分别是[2a, 2b.] 所以各边的比都是[ab,] 三个内角分别是45°,45°,90°,各角分别相等,所以这两个三角形相似.
展示4:如图6,△ABC与△DEF的形状完全相同,它们的各角分别相等,各边的比都等于1,所以△ABC和△DEF相似.
【说明】例子在概念教学中至关重要,一个好的例子胜过千万条说教. 在教学中,得出相似形的概念之后,让学生举例,并推理论证,这是理解概念和运用概念的过程,也是概念从理性的抽象走向理性的具体,从形式化抽象走向形式化具体的过程.
二、从数学抽象的角度审视教学
数学学习是一个抽象的过程,大到一个数学体系的公理化,解决实际问题的模型化,小到一个概念的定义,一个证明技巧的发现等都需要数学抽象. 正如史宁中教授所说,数学在本质上研究的是抽象的东西,数学发展所依赖的最重要的基本思想也是抽象. 上述案例中,相似形概念形成、理解与应用的过程,其实就是一个数学抽象的过程.
1. 求同舍异——概念的弱抽象
在数学思想活动中,有一类方法是在同类的事物中抽取关于数量、空间形式或结构关系方面的共同属性,舍弃其他的特征,从而形成新的数学概念. 这种舍弃一部分属性保留共同属性的抽象过程称之为“弱抽象”. 例如,在教学片断1中,“形状相同”是不同图形的共同属性,而三角板、正方体等名称,以及大小相等或大小不等,立体或平面等,都是不同属性而被舍弃. 也就是说,相似形概念的形成过程正是弱抽象的过程.
在初中数学的概念教学中,弱抽象非常普遍. 弱抽象形成概念的关键是归纳概括. 因此,在教学中,教师首先应该提供丰富的、典型的事例;其次,要给予学生充分的时间观察、比较、交流,这是培养学生归纳概括能力的过程. 在“相似形”一课的教学中,教师提供了学生熟悉的图形,这些图形从生活到数学,从立体到平面,从不全等到全等,丰富而典型. 在一系列活动的基础上,通过师生交流、生生交流,最后提炼“形状相同”的共同属性. 这正是积累数学抽象活动经验,发展数学核心素养的过程.
2. 增添内涵——概念的强抽象
在数学思想活动中,有一类方法是将新的特征或属性添加到已有的数学结构中,从而形成新的数学概念. 这种通过在原有数学结构中增添新的性质来获得新的数学概念的过程,称之为“强抽象”. 例如,边数相同的多边形增加“各角分别相等和各边成比例”的条件属性,从而形成相似多边形的概念. 随着内涵的增加,外延随之缩小. 由此可见,相似多边形概念的形成正是数学强抽象的结果.
强抽象在初中数学概念的教学中十分常见. 强抽象使原有数学对象的内涵更加丰富,但这种丰富不是具体的,而是抽象的. 鉴于上述特点,教学中为了帮助学生理解概念,首先,应提供丰富而具体的事例. 在教学片断2中,学生列举了大量的例子,先是举反例,如“各角分别相等的四边形不一定相似”“各边成比例的四边形不一定相似”,然后举正例,如展示1、展示2、展示3、展示4. 具体的事例有助于学生深刻理解相似多边形的概念. 其次,因为增加了内涵条件才有了新概念,才有了新概念的外延和性质,所以新增的内涵条件应该是教学的重点,抓住新增的内涵条件也就抓住了新、旧概念之间的关系,也就能够实现有意义的知识建构. 教学中,学生所列举的例子都是围绕各角分别相等和各边成比例来证明图形不相似或相似,有效促进了学生对新的抽象概念的理解.
3. 引进符号——抽象的形式化
数学对象不仅是抽象的思想材料,还是形式化的思想材料. 所谓形式化,是指这些抽象的思想材料是用数学符号语言组织起来的,当人们面对一系列数学材料时,看到的仅仅是材料的形式,其所包含的真正内容却是抽象的思想隐藏在形式之中. 例如,从直观上看,“∽”就是一个符号,但它在数学中的真实含义是指两个图形之间满足如下关系:图形的形状相同(定性);或者是边数相同的多边形,各角分别相等,各边成比例(定量). 但是单从符号的形式上看不到它的真实含义,这一点也正说明了符号的抽象性.
数学符号是在数学抽象的基础上逐步引入的,并以此为基础把数学对象的研究转化为数学符号的研究. 数学符号是数学抽象的产物,同时也使数学更加抽象. 史宁中教授认为抽象有两个层次:一是直观描述;二是符号表达. 数学概念需要用文字语言阐述,数学概念通常也会用简约的符号语言表述,使数学抽象走向形式化,这是数学的特点,贯穿于数学学习的始终. 而理解这种形式化正是进一步学习数学的基础. 上述案例中,教师在引入符号“∽”时,介绍了“∽”的历史,以及“∽”与“≌”的关系,明确了“∽”的意義. 并以三角形相似进行举例:在[△ABC]和[△A′B′C′]中,因为[∠A=∠A′,∠B=∠B′,∠C=∠C′, ABA′B′=BCB′C′=][CAC′A′,] 所以[△ABC∽△A′B′C′,] 反之亦然. 将“∽”与[∠A=∠A′,][∠B=∠B′,∠C=∠C′]等已有的符号之间建立联系,有利于学生理解相似符号“∽”的形式化意义.
4. 有效联系——抽象的具体化
数学概念是抽象的,数学概念的抽象性增加了它的理解难度,也成为数学学习的障碍. 其实,数学概念也是具体的. 首先,数学概念定义的对象是具体的,它是对客观世界数量关系和空间形式的表述;其次,任何一个数学概念都是用具体的语言描述的. 也就是说,数学概念其实是抽象与具体的统一. 例如,相似的概念是抽象的,但相似的内容是用具体的语言描述的,相似的图形也是具体存在的.
对学生而言,如果新的概念始终停留在抽象层面,很难说他已经理解了概念,只有当新概念从抽象走向具体,学生才是真正接受它,并能灵活运用它,才能成为学习更抽象知识的基础. 否则,只会是机械模仿、生搬硬套. 如何使新的概念从抽象走向具体?笔者认为通常有两条路径:建立新概念与现实世界之间的联系;建立新概念与旧知识体系之间的联系. 而举例与推理是建立这种联系的常用方法. 在上述案例中,相似形概念的形成基于观察典型的例子,然后教师又安排了一组围绕“形状相同”的图形特征的练习,在图形的观察与辨析中理解相似;而在相似多边形的概念教学中,学生列举了4个典型的例子. 在教学中,这样的具体例子能帮助学生理解概念,感受相似的具体存在,在新概念与现实世界之间建立有效联系. 在证明多边形相似的推理论证中,相似与边和角、相似与全等等原有知识之间建立了有意义的联系. 这是应用概念的过程,是理解概念的过程,更是相似形的概念从抽象走向具体的过程. 可以说,举例与推理使新概念从理性的抽象走向理性的具体,在两者之间建立了有效的联系.
概念教学是数学教学的基石,而形成概念的过程正是数学抽象的过程. 理清数学概念形成中的不同抽象形式及过程,才能在教学中有的放矢,培养学生的数学抽象能力才能从不自觉走向自觉.
参考文献:
[1]中华人民共和国教育部制定. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2018.
[2]涂荣豹. 数学教学认识论[M]. 南京:南京师范大学出版社,2003.
[3]涂荣豹,王光明,宁连华. 新编数学教学论[M]. 上海:华东师范大学出版社,2006.
[4]郑正亚. 数学抽象概念教学随笔[J]. 数学教育学报,1999,8(1):75-78.
[5]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[6]史宁中. 数学基本思想18讲[M]. 北京:北京师范大学出版社,2016.

