基于范希尔理论的教学分析与设计

孙凯

摘  要：范希尔理论的核心内容是几何思维的五个水平及与之对应的五个教学阶段. 以“轴对称图形”章头导学为例，基于对范希尔理论的理解，在章头导学中设计“欣赏感悟、操作探究、作图描述、应用延伸、创意设计”等阶段性活动，有助于发展学生对应的几何思维水平.

关键词：范希尔理论;章头导学;设计意图;几何思维

苏科版初中数学教材在每个章节的起始位置都设计了章头图和章引言（以下统称“章头材料”）. 章头材料由丰富多彩的图表和言简意赅的文字组成，它是对整章内容的高度概括，在渗透德育、连接前后知识、激发学习兴趣、发展认知结构等方面有重要作用. 章头导学是指以章头材料为内容、以知识为载体、以结构为目标的课堂教学形态，是对全章教学内容的浓缩，起到了引导、简介、导览的作用，帮助学生在最短的时间内了解内容的本质. 对章头材料教育教学价值的挖掘与利用，能帮助学生了解整章学习的内容和结构，明晰所学内容的“来龙去脉”，掌握学习的具体方法，发展学生的数学思维能力. 基于范希尔理论的内涵分析，下面以“轴对称图形”章头导学为例，阐释理论运用于教学实践的分析与设计.

一、范希尔理论的内涵

荷兰教育家范希尔夫妇（Pierre Van Hiele&Dina Van Hiele）曾在几何教学中遇到一些普遍性的问题，在皮亚杰的认知理论影响下，结合自身的教学实践，研究并提出几何思维的五个水平及与之对应的五个教学阶段，被称为范希尔理论（几何思维水平理论）. 五个几何思维水平分别是水平0（视觉）、水平1（分析）、水平2（非形式化的演绎）、水平3（形式的演绎）、水平4（严密性）;对应的五个几何教学阶段分别是阶段1（提供信息）、阶段2（特定方向）、阶段3（解释）、阶段4（自由探索）、阶段5（整合）. 几何思维水平理论可以用来诊断学生的几何思维水平，也可以用于教学活动的设计. 在初中几何教学中，五个几何教学阶段分别对应“整体地认识几何对象、分析几何对象的要素与特征、通过幾何性质认识几何对象、利用演绎推理证明几何关系、归纳描述几何对象”五个方面.

二、教学分析

1. 教学内容分析

“轴对称图形”是苏科版《义务教育教科书·数学》八年级上册第二章的内容，其章头材料由4幅图片、2段引言和2个活动要求构成.

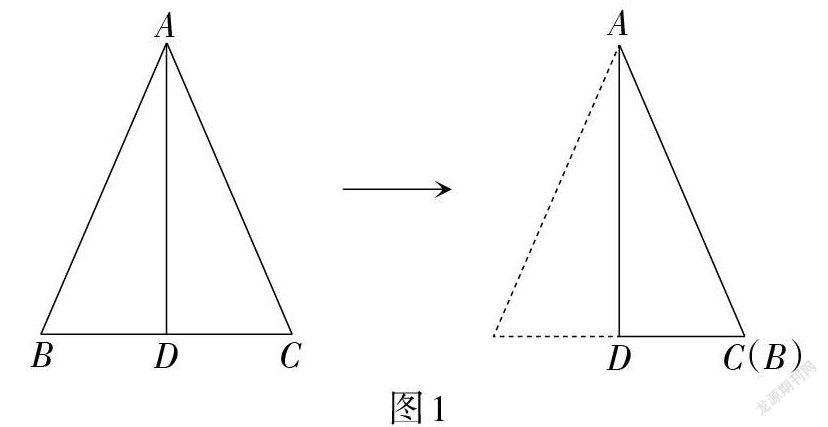
图1为等腰三角形ABC，根据图形可知，△ABC沿AD折叠后点B与点C重合，进一步可得AD⊥BC，BD = CD. 此图意在引导学生通过折叠思考AD⊥BC，BD = CD的依据是什么，既能引发学生对轴对称图形特征与性质的思考，又能引导学生感受利用轴对称性探索并证明图形的性质是本章学习探索的基本路径与方法.

图2是北京天坛，运用美轮美奂的古代建筑引导学生欣赏轴对称之美，使学生学会用数学的眼光观察和欣赏生活，传播数学文化，挖掘数学的育人功能.

学生通过活动1中的观察、折叠、剪纸等活动，经历从空间想象到直观操作的活动过程，感受轴对称图形的共同特征，给出轴对称图形的概念. 活动2是让学生按活动操作，探索、归纳轴对称图形的性质. 引言部分指出生活中的轴对称之美及探索轴对称图形性质的具体方法，指明本章主要学习的内容.

章头材料提供的信息基本蕴含了为什么学、怎么学、学什么的核心内容. 范希尔理论启示我们，学生几何思维水平的发展具有次序性和进阶性等特点. 因此，教学内容的编排与教学活动的组织应与几何思维水平的层级相对应，使学生的几何思维水平由低向高呈螺旋式发展.

2. 学生学情分析

在小学学段，学生已经学习过轴对称图形的相关知识，现在我们对三个学段中关于轴对称图形的内容进行简单的分析. 根据《义务教育数学课程标准（2011年版）》的要求，在第一学段（1 ～ 3年级），主要是通过生活实例感受轴对称现象;在第二学段（4 ～ 6年级），通过观察、操作等活动，进一步认识轴对称图形及其对称轴，能在方格纸上画出轴对称图形的对称轴，能在方格纸上补全一个简单的轴对称图形;在第三学段（7 ～ 9年级），通过具体实例了解轴对称的概念，探索它的基本性质，能画出简单平面图形关于给定对称轴的对称图形，了解轴对称图形的概念，探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质. 三个学段分别使用了“感受、认识、探索”三个关键词进行表述，由此对三个学段的学习要求有了清晰的认识. 从范希尔理论的视角分析可知，初中阶段的学生已初步具备几何思维水平0、水平1，即能通过整体轮廓辨认图形，能在方格纸上补全图形，能用图形的特性解决简单的几何问题.

3. 目标及目标解析

本节课的教学目标设计如下.

（1）欣赏现实生活中的轴对称现象和轴对称图形，感受轴对称之美;

（2）在操作活动中了解轴对称图形的概念，会确定对称轴，通过操作探索轴对称图形的性质，感悟轴对称性;

（3）能画出简单平面图形（点、线段、直线、三角形）关于给定对称轴的对称图形;

（4）运用轴对称的性质解决简单的几何问题;

（5）利用轴对称设计简单的图案.

目标解析：章头导学的核心任务是导学，具体目标包含整章知识结构与内容，使学生通过学习了解整章知识体系与要求，在具体的问题情境中了解研究对象及研究方法，为后续学习做好铺垫. 教学目标的设计要充分尊重学生的几何思维水平，由低到高、由易到难、循序渐进，逐层提高，符合学生的认知发展规律.

三、教学价值取向分析

1. 合理设计活动阶段，发展几何思维

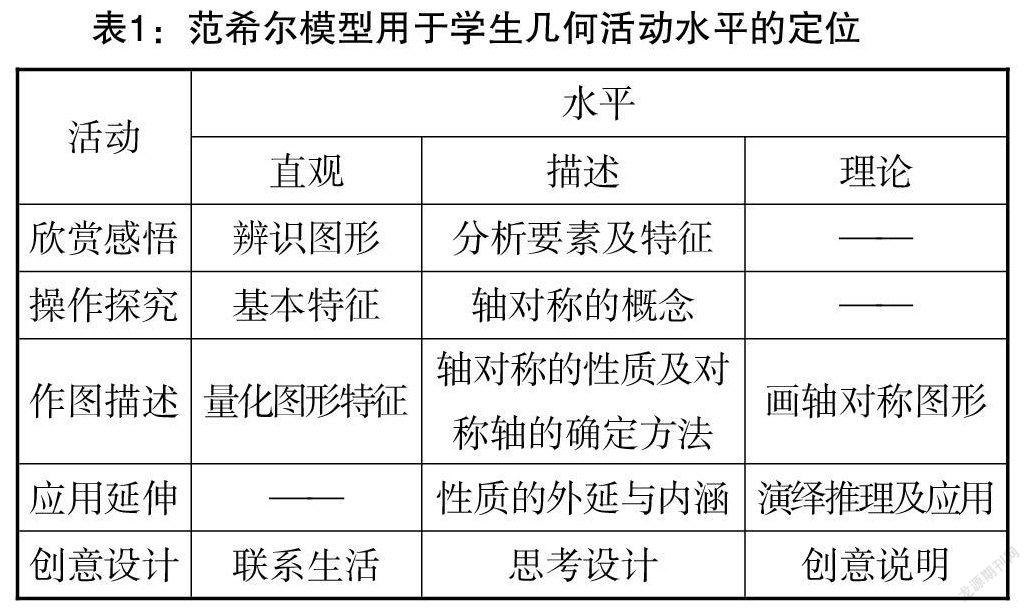
在有关学生几何概念发展与学习的研究中，范希尔的几何思维水平体系是最具影响力的理论之一. 范希尔对几何思维水平的分类一般分为“五水平分类法”和“三水平分类法”（直观、描述、理论），虽分类结果不同，但其本质是相同的. 基于学生的几何思维特征及教学设计需要，本文中的范希尔模型采用了“三水平分类法”分析，五个教学活动阶段则采用了“五水平分类法”阐释. 在章头导学教学中，如何设计阶段性教学活动取决于学生的几何思维水平发展定位，阶段性教学活动应与几何思维水平的层级相对应，活动的目的是适当引发学生的思维危机，使学生的几何思维水平由低向高螺旋式提升. 因此，将“轴对称图形”一课的教学活动设计为如表1所示的五个阶段：提供信息的活动（欣赏感悟）、特定方向的活动（操作探究）、解释活动（作图描述）、自由探索活动（应用延伸）、整合活动（创意设计）.

2. 合理设计问题情境，发展探究能力

导学有度是章头导学课的基本追求. 所谓“有度”，指的是适可而止，尊重学生学习的认知规律，问题情境合理有效，紧贴最近发展区. 基于对章头材料的研读与理解，结合范希尔理论，确定“轴对称图形”一课导学的主要任务有三个：一是在提供信息的问题活动中引导学生欣赏轴对称图案，感受数学有用、数学很美;二是引导学生在特定方向和解释的问题活动中经历折叠、剪纸、折纸、扎孔等操作活动，了解轴对称图形的概念，初步探索线段、角、等腰三角形等轴对称图形的性质;三是在自由探索和整合活动中以问题为主线，引导学生运用轴对称性质探索并解决经典的几何图形问题. 其中，利用轴对称性探索与证明相关性质是导学的核心. 在教学中，教师应引导学生初步探索相关性质，使学生“既见树木，又见森林”，优化学生的认知结构，布局整章知识网络. 在探索轴对称图形性质的活动中，应把握好导学的度，适可而止，不必深究，引导学生理解掌握探索问题的基本策略与方法是关键.

3. 合理设计操作活动，发展直观想象素养

范希尔理论启示我们，几何教学离不开直观形象的操作活动，亲身经历操作活动对学生几何思维的发展至关重要. 在课堂教学中，教师对电脑、白板、课件、互联网等多媒体的依赖越来越严重，甚至出现不用多媒体不知道如何上课的怪现象. 多媒体教学推动了数学教学的改革与发展，其积极意义毋庸置疑，但是过度依赖也会产生一些负面影响. 因为人的学习是有快慢之分的，单纯依赖技术性的快不一定符合学生的认知规律，学生自主学习获取知识的能力是技术过程代替不了的. 初中数学知识大多来源于几千年来人类的生产、生活实践，运用实践操作的方式学习数学知识具有重要意义. 正所谓：纸上得来终觉浅，绝知此事要躬行. 学生只有亲历实践操作过程，才会深刻感受轴对称图形的特征，给出的概念才有“物质”基础，性质探索的路径和方法才会明晰，几何思维水平的发展才会水到渠成. 因此，章头导学设计应基于学生的认知规律，合理设计手脑结合的操作实践活动，搭建自主学习的平臺，发展学生的直观想象素养.

四、教学活动设计

教师引言：小学阶段我们学习过轴对称图形的相关知识，在生活中存在很多轴对称现象或轴对称图形，你能举几个例子吗？

1. 欣赏感悟（提供信息的活动）

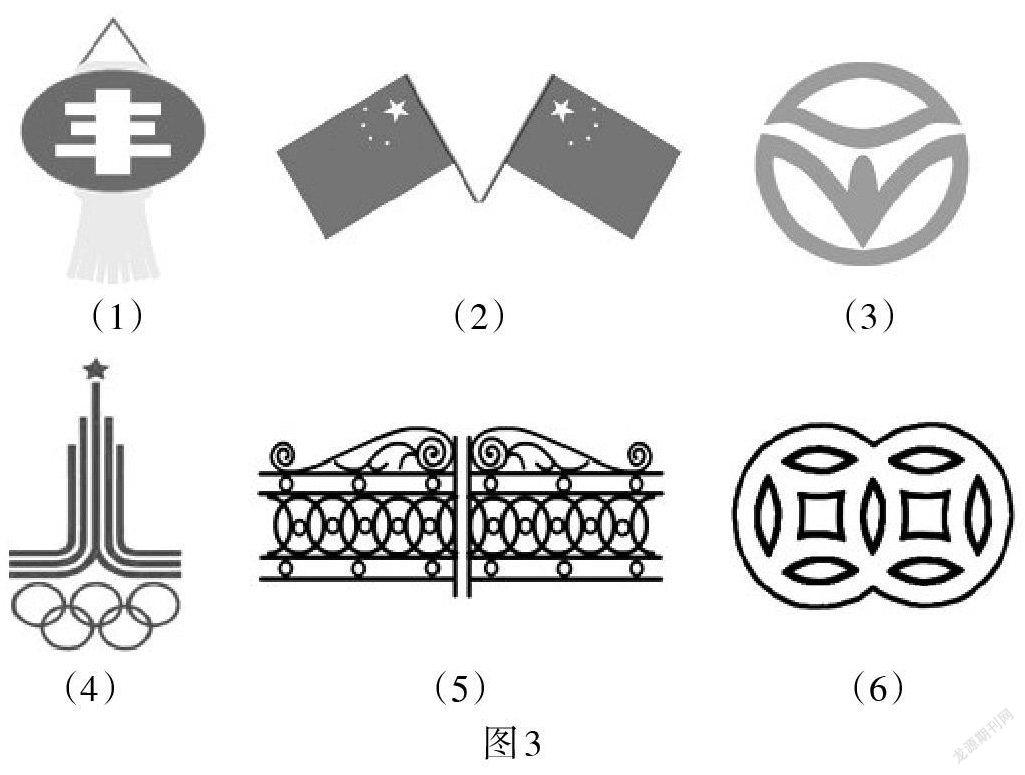
欣赏图3中的图形，观察并归纳图形特征.

【设计意图】为学生提供丰富的生活图形信息，刺激视觉，展示轴对称之美，引导学生切身感受数学是有用的、数学来源于生活，激发学生的学习兴趣，引导学生初步感悟轴对称图形的基本特征，发展视觉思维.

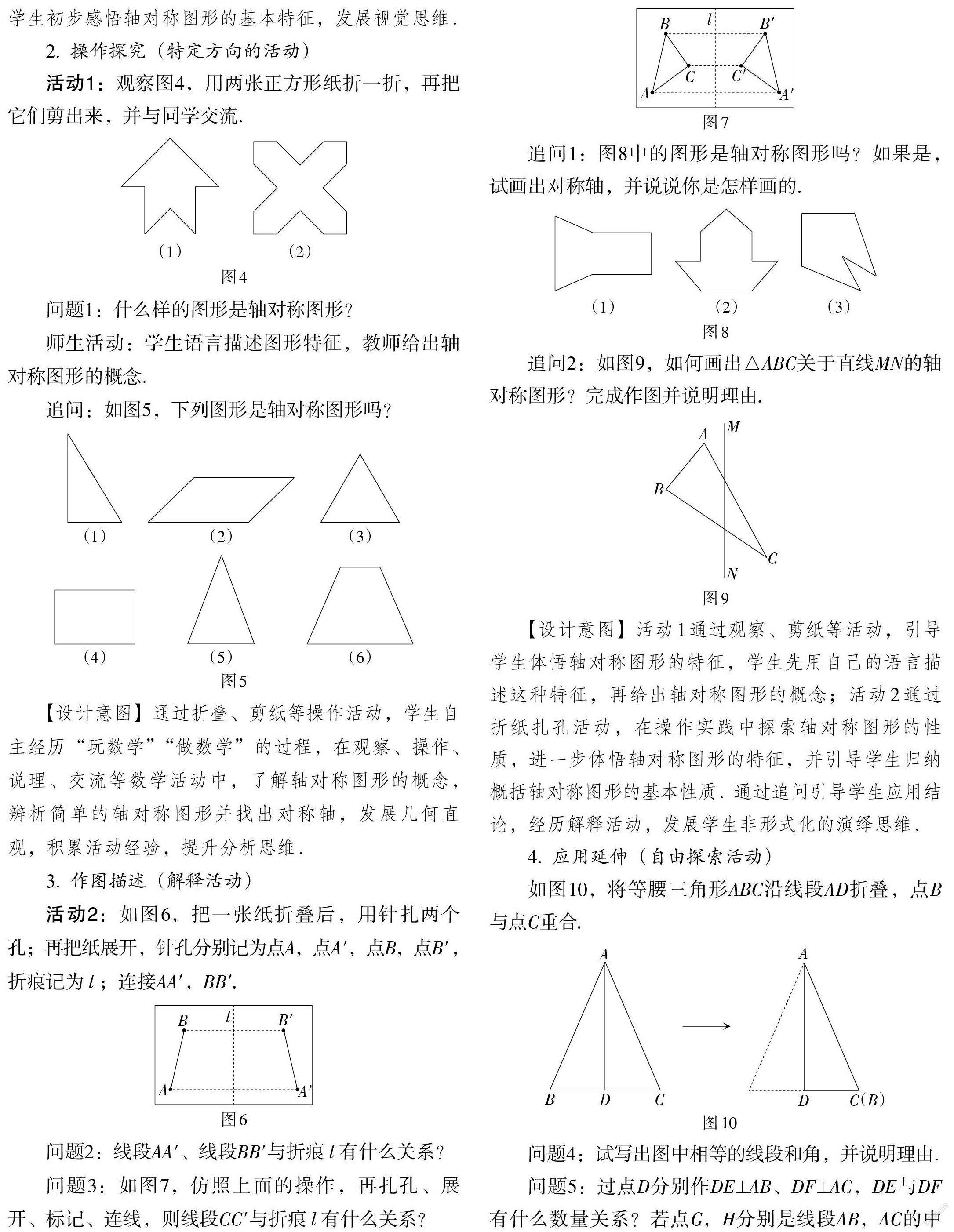
2. 操作探究（特定方向的活动）

活动1：观察图4，用两张正方形纸折一折，再把它们剪出来，并与同学交流.

问题1：什么样的图形是轴对称图形？

师生活动：学生语言描述图形特征，教师给出轴对称图形的概念.

追问：如图5，下列图形是轴对称图形吗？

【设计意图】通过折叠、剪纸等操作活动，学生自主经历“玩数学”“做数学”的过程，在观察、操作、说理、交流等数学活动中，了解轴对称图形的概念，辨析简单的轴对称图形并找出对称轴，发展几何直观，积累活动经验，提升分析思维.

3. 作图描述（解释活动）

活动2：如图6，把一张纸折叠后，用针扎两个孔;再把纸展开，针孔分别记为点A，点A′，点B，点B′，折痕记为[l];连接AA′，BB′.

问题2：线段AA′、线段BB′与折痕[l]有什么关系？

问题3：如图7，仿照上面的操作，再扎孔、展开、标记、连线，则线段CC′与折痕[l]有什么关系？

追问1：图8中的图形是轴对称图形吗？如果是，试画出对称轴，并说说你是怎样画的.

追问2：如图9，如何画出△ABC关于直线MN的轴对称图形？完成作图并说明理由.

【设计意图】活动1通过观察、剪纸等活动，引导学生体悟轴对称图形的特征，学生先用自己的语言描述这种特征，再给出轴对称图形的概念;活动2通过折纸扎孔活动，在操作实践中探索轴对称图形的性质，进一步体悟轴对称图形的特征，并引导学生归纳概括轴对称图形的基本性质. 通过追问引导学生应用结论，经历解释活动，发展学生非形式化的演绎思维.

4. 应用延伸（自由探索活动）

如图10，将等腰三角形ABC沿线段AD折叠，点B与点C重合.

问题4：试写出图中相等的线段和角，并说明理由.

问题5：过点D分别作DE⊥AB、DF⊥AC，DE与DF有什么数量关系？若点G，H分别是线段AB，AC的中点，则DG与DH有什么数量关系？

问题6：若在线段AD上任取一点P，连接PB，PC，则PB与PC相等吗？为什么？

追问：如图11，等腰三角形ABC沿线段AD折叠，点B与点C重合，若AE = AF，则DE与DF相等吗？

【设计意图】本环节借助章头材料中给出的图1设计层层递进的问题串，驱动学生自主探索相关线段、角之间的数量关系，经历利用轴对称性探索并证明图形的性质的活动过程，帮助学生进一步理解轴对称图形的轴对称性，积累宝贵的数学活动经验，发展形式的演绎思维，也为后续整章学习打下良好基础.

5. 创意设计（整合活动）

试利用轴对称的性质设计一幅作品.

【设计意图】运用所学轴对称知识自主整合创作，通过动手画图发展学生的作图技能、创新意识、应用意识，发展学生思维的严密性，提升学生的数学素养，使学生逐步形成研究几何图形的基本思路，即“概念—判定—性质—应用”.

总之，范希尔理论与几何章头导学的结合，使教学形式更灵活、教学活动更高效、教学效果更显著. 对范希尔几何思维水平理论的教学研究有助于提升学生的思维水平，更有助于提升教师的几何教学设计水准.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]鲍建生，周超. 数学学习的心理基础与过程[M]. 上海：上海教育出版社，2009.

[3]曾友良，贠朝栋. 范希尔理论的几何思维水平研究综述及启示[J]. 当代教育理论与实践，2017，9（5）：12-16.

[4]丁保媛，刘咏梅. 范·希尔理论指导下的函数概念教学[J]. 中学数学研究，2013（3）：1-3.