高中数学解题错因分析及对策
阮莲花

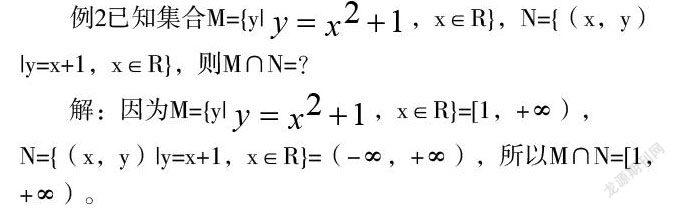




摘要:学生做题时产生错误的原因可能有多种。主要分为智力因素和非智力因素两大类。如对一些概念性质模糊,忽视了一些公式定理成立的条件,违反了证明规则。不能正确的运用数学思想方法如分类讨论考虑不全面;审题不清,由于惯性思维对题目主观臆断[1];对公式机械记忆导致混淆错误运用;由于粗心大意导致的错误。本文通过一些典型的例题对应分析学生做题产生的错误原因并提出纠错策略,以帮助学生找到薄弱点提高数学成绩和为教师教学提供一点启示。
关键词:数学解题;错因分析;纠错策略
引言
数学以其特有的思维性,令许多学生望而生畏,尤其是高中数学。但是其实不管什么学科,都有一定的方法蕴含其中,只要理解掌握了,数学可以成为你的优势学科,数学能通过人的逻辑推理和分析思维能力,学好数学也有助于学好物理和化学。在解题中,一道题中可能涉及了一些数学思想方法及一系列的定理公式和概念性质的应用。很多人不停地刷题锻炼自己的能力,事实上大部人做完成堆的题效果并不明显,是因为他们抓不住重难点,没有真正理解和掌握总结,刷再多题也是无用功,题不在于多而在于精。学好数学重要是方法和知识体系的前后联系,学会总结反思,把一些题和方法归类,深入理解和巩固。在学习和做题中反思分析错题错因是很有必要的,对于学生而言可以找到自己的薄弱点,对症下药;对于教师可以发现学生的错误反思和改进教学,充分备课。下面结合自己的实践体验分析一些易错题的错因及相应的教学改进策略。
一、对一些概念性质模糊导致的错误
这是学生学习过程中出错的一个重要原因,学习概念时没有理解概念的内涵和外延,不能把握准概念。一些看似简单的题目,稍微变式一下,做题就感到模棱两可,所以一定要深入理解概念。
例1设M={1、2、3},N={e、g、h},从M至N的四种对应方式,其中是从M到N的映射是(B)
错因分析:本题考查映射的概念和特点,学生出现错误的原因是对映射的概念和特点不清楚,以及与函数概念的联系和区别模糊。对映射是否能一对多还是多对一混淆。根据映射的特点不能“一对多”:A中不能有剩余元素,B中可以有剩余元素。所以A、B、D都错误;只有C完全满足映射与函数〈特殊对应)的全部5个特点。
教师在讲解概念和这类题目时应举一些例子,使学生在完全掌握概念的基础上,灵活掌握变型题。并且讲清楚映射和函数的联系和区别以及各自的特点,引导学生观察对比区别他们的不同之处,深入理解记忆。函数是特殊的映射,是数集到数集的映射,映射是函数概念的扩展,映射不一定是函数。映射与函数(特殊对应)的共同特点:可以是“一对一”;可以是“多对一”;不能“一对多”。
错因分析:出现错误的原因是没有注意到构成两个集合的元素是不同的,即集合M是数集,而集合N是点集,两个集合是性质完全不同的集合,不能做运算。
因为集合N是一个点集,不是数集,即集合N表示直线y=x+1上所有的点,而不是(一∞,+∞)。所以集合M∩N=0。
集合的概念是高中数学最基础的概念,集合知识是为后续学习做准备的基础知识。教师在讲解集合知识的时候,应着重讲解集合的性质,特别需要教师强调的是构成集合元素的特征。
二、对于一些公式定理理解不清或混淆而导致的错误
没有注意公式定理的前提条件,从而扩大其使用范围等,都可能导致解题出错。如利用均值不等式求最值时,对一正二定三相等的条件理解不透彻,忽略了求最值的法则及不等式成立的条件而导致错误结果[2]。学生往往会因为忽视这三个条件中的某个而出错。
学生1:因为|a-b|=|b|,所以a-b=b或a-b=-b,故a=2b或a=0(舍去),所以|a-2b|=0,由于b是非零向量,所以|2b|>0,故|2b|>|a-2b|,选A。
学生2:因为|a-b|=|b|,所以(a-b)(a-b)=b·b,a·a-2a·b+b·b=b·b,
所以a·a=2a·b,所以a=2b,故|a-2b|=0。由于b是非零向量,所以|2b|>0,故|2b|>|a-2b|.選A。
教师在讲解该内容时可以引导学生画图,数形结合可以使学生更直观的理解和比较大小关系。说明向量运算与实数运算的本质区别,向量运算不仅涉及向量的长度,还涉及向量的方向。在实数运算中,若a≠0且ab=0则b=0。但在向量运算中若a≠0且ab=0则有两种情况b=0或a⊥b[3]。
三、运用数学思想方法如分类讨论考虑不全面
分类讨论是解决问题的一种逻辑方法,也是一种数学思想,这种思想对于简化研究对象,发展人的思维有着重要帮助。分类讨论是具有较高的逻辑性及很强的综合性,培养学生思维的条理性,缜密性,科学性,所以在数学解题中占有重要的位置。分类原则:分类对象确定,标准统一,不重复,不遗漏,分层次,不越级讨论[4]。但是在解题中学生容易因为分类标准和层次不清楚而导致一些错误。
错因分析:该学生没有考虑直线L的斜率不存在的情况。可能出现的原因有以下几点:①该学生忽略了直线点斜式方程的局限性(点斜式方程不能表示斜率不存在的直线);②该学生对分类讨论思想的运用不熟练:③该学生对圆与直线的位置关系考虑得不全面。
正确解法:①当直线L的斜率不存在时,根据题意所求直线l的方程为x=2;②当直线L的斜率存在且设为k时,方法如上。综上,所求直线L的方程为x=2或4x-3y+1=0
教师应该根据该题的教学步骤,在教学过程中,采取相应策略设置问题。
教师提出问题,“过圆外一点能作几条圆的切线”,让学生画出该题相关的图像,“直线L与圆相切有几种情况?”引导学生根据直线斜率的存在情况运用分类讨论思想解题,可设置问题如“当斜率存在时,直线L的方程如何求得?”当斜率不存在时,直线L的方程是什么?
四、审题不清,由于惯性思维对题目主观臆断;对公式机械记忆导致混淆错误运用;由于粗心大意导致的错误
例7已知双曲线的右准线为x=4,右焦点F(10,0),离心率e=2,求双曲线的方程。
五、总结
总的来说,我认为教师可以从以下几点着手①在新知识的教学时注重突出基础知识、基本概念,在学生知识和思维的薄弱点设置教学环节,说明相关概念之间的联系和区别,加入适当的变式练习,帮助学生真正掌握知识点。深入理解公式定理的成立条件和证明过程,不能停留在机械表面的记忆层面。②在日常学习、练习中养成正确的学习习惯和思维习惯。比如,整洁的草稿纸是理性思维的外在表象。做题时不是一味求快,要认真仔细,适当的时候“瞻前顾后”,把握整体,对已知条件、已得结论、所求结果等统筹把握,而不是想到什么写什么。在易错点、特殊点处能重点对待,引导学生总结反思,及时纠正错误。③养成良好的心态。考试中由于紧张的气氛和时间的限制会出现-些“粗心”,会把“+”误写成“一”,“<”误写成“>”等。因此,在日常学习中养成良好的心态也是减少做题出错的关键。
参考文献:
[1]刘发.初中数学易错题错因分析及纠错策略[J].数学教学通讯,2015(000)004.
[2]何彩云.用基本不等式求最值的常见错误例析[J].教育科学,2014(01)
[3]徐静.高中数学解题错误的原因分析及对策[J].数理化学习,2018(11)
[4]赵新五.浅谈高中数学分类讨论中的易错点[J].试题与研究,2011(10)

