基于Matlab的曲柄摇杆机构参数化设计

李世文 王力强 潘鑫 谭积明 翰林 李国和

摘要：本文通过一个设计案例，论述如何利用Matlab 进行机构的参数化设计，并应用于实际作品中。理论联系实践，首先进行机构整体设计，用数学公式推理出各参数的关系，再进行数学建模，综合考虑各参数对运动的影响，进行合理优化，完成参数化设计。

关键词：曲柄摇杆;参数化设计;数学建模;实践

中图分类号：U463                                     文献标识码：A                                文章编号：1674-957X（2021）05-0204-03

0  引言

Matlab是美国MathWorks公司出品的商业数学软件，用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人、控制系统等领域，应用十分广泛。对于产品设计，通常需要结合实践经验进行总体设计，选择合理的机构、传动形式、运动部件等，对于零部件具体尺寸、传动比等则需要经过准确的计算。对于同系列同类型的设计通常采用一个方案，对其中部分零件做优化设计，从而满足不同场合，不同条件下的应用。比如大家熟悉的曲柄摇杆机构，通过改变其中一个杆长或几个杆长同时改变，其输出轨迹会有很大差异。而这些杆长微小的变化不能全靠经验，需要进行准确的计算，并进行轨迹验证，这就需要利用一款分析计算软件结合设计实践经验，进行合理的优化设计。本文以一个实际案例介绍其具体应用。

1  总体设计

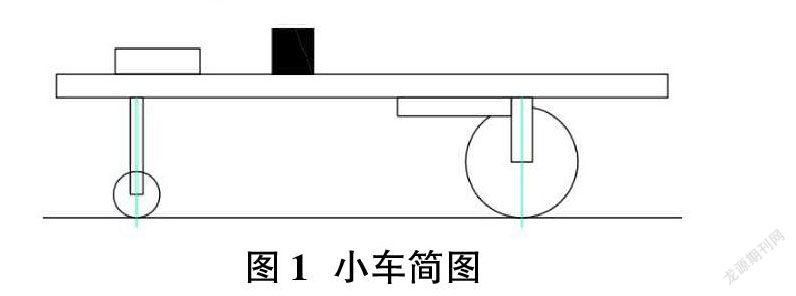
总体设计就是结合实际需要实现相应功能，设计及选择合理的机械结构，组合成一个完整的运动机构。本案例中需要设计一款纯机械的三轮可越障的小车，要求小车有转向功能，对比几种常用机构，选择曲柄摇杆机构作为转向机构，如图1所示。

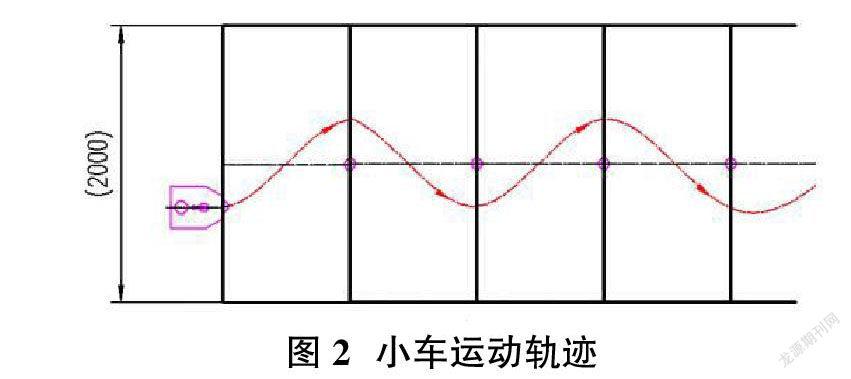
小车前轮为转向轮，后轮为驱动轮，假设小车为一个质点，其在固定驱动力作用下做周期运动，如图2所示。

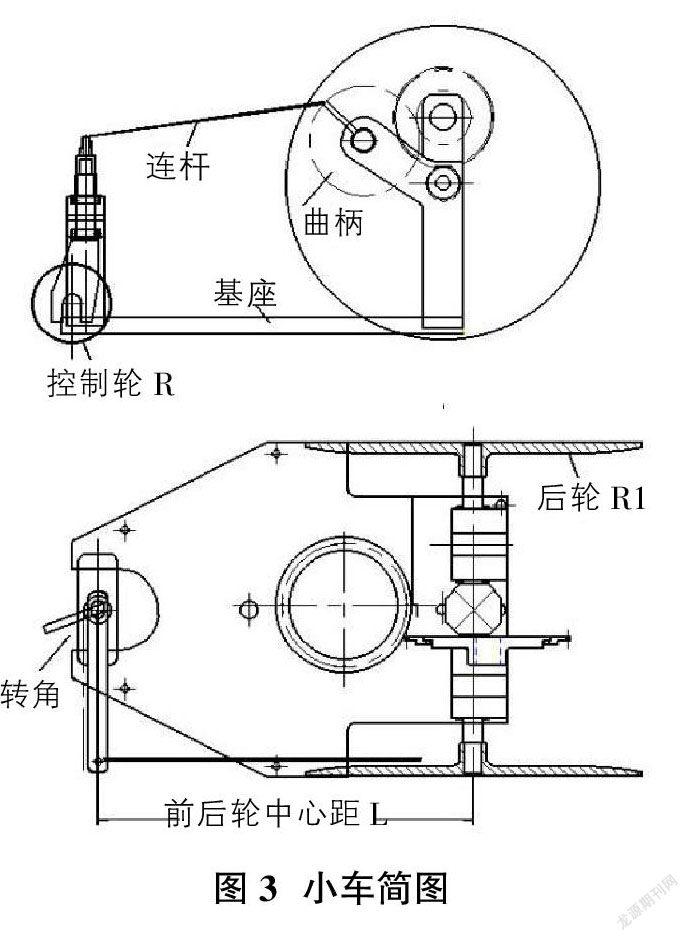
从图2可以发现，其轨迹近似为正弦曲线，小车能够通过方向控制机构-曲柄摇杆机构控制前轮周期性转向，从而绕过图中方格交点位置的障碍物。障碍物之间的间距是变化的，从700-1300mm。根据小车整体结构的需要，根据经验总体设计一部三轮小车，其简图如图3所示。

图3中各零件尺寸需根据小车运动情況及绕过障碍物的间距的变化而变化，需要进行优化。首先明确可调整部件及其运动关系，再用公式表达，用数据表达运动构件之间的关系，就可以进行优化了。从小车简图中可以发现，核心的机构就是一个曲柄摇杆机构，小车底盘与立柱组成支架，为固定件，曲柄长度与连杆长度可以调节，它们决定了摇杆也就是前轮的摆角。前轮为转向轮，控制整个小车的运动轨迹，所以需要对这个曲柄摇杆机构进行建模，通过计算进行优化。

2  轨迹分析及数学建模

根据设计方案，假设小车为一个质点，则根据平面内质点运动规律。假设xOy平面内的质点P在t=0时刻的位置为;在任意时刻t速度矢量已知，为。如何确定质点运动轨迹呢？小车近似看作自行车，若自行车前进方向不变，则前后轮都沿直线运动，二者轨迹（即车轮与地面接触点的轨迹）在同一直线上;若自行车前进时前轮左右摆动，则前后轮轨迹不同。自行车前轮与后轮大小若相同，两轮子轴的距离为定值L，即前后轮与地面接触点之间的距离大小相同。后轮为主动轮，前轮可左右摆动，t时刻与后轮的夹角为？兹（t），左转角度为正，右转角度为负。在xOy平面内，后轮在t时刻的位置用X（t）表示，前轮在t时刻的位置表示。自行车后轮旋转线速度为定值，设为1，这里需要考虑几种情况：

①在t时刻，前后轮的位置有何关系？写出方程。

②在t时刻，用？琢（t）表示后轮运动方向与X轴正向的夹角，前轮运动方向与X轴的夹角如何表示？前后轮的速度矢量的关系是什么？前轮旋转线速度多大？

③将前后轮的位置函数X（t），Y（t），与方向角？琢（t），？兹（t）等建立微分关系。

④假设t=0时，后轮的位置为X（0）=[0，0]T，后轮方向角？琢（0）=0;前轮方向角与时间的函数已知为？兹（t）=sint，t？叟0，L=1，研究前后车轮与平地接触点的轨迹，给定初始位置和每一时刻车头（前轮）相对车身的角度。

这里需要注意，车轮方向与轨迹切线方向相同，设后轮轨迹曲线X（s），参数为该曲线的弧长参数，故切线方向为X（s），已单位化，也是后轮的方向;按理说对时间求导才能用点，我这里为图个方便前轮轨迹Y（s），它的切线方向，这里要单位化，因为参数只是与后轮轨迹弧长有关。这样得到一个几何位置关系：

其中L表示前后轮之间的距离，这是由自行车决定的，

令表示后轮与前轮的方向，则有姿势关系：（1）

其中，？兹（s）表示后轮在s 时，前轮的偏转角，左转为正，右转为负。

根据式（1）、式（2）两方程就能决定车轮的运动轨迹。用角度表示方向，？茁（s）表示后轮的角度，？兹（s）表示前轮相对偏转角，则前轮角度？茁+？兹，

基本微分方程：

（2）

后轮速度（3）

前轮速度，为单位向量（4）

其中，对（2）再求导，得即

求得此可得解几个微分方程组成的方程组得到如下关系式：R：控制轮半径，l：连杆长，r：曲柄长，R1：后轮半径，W1=S/R1后轮转角，W=W1 /（2.52·R1），控制轮转动角度

3  参数化设计

根据求得的参数表达式，编写程序，用Matlab进行仿真优化，程序如下。

function f=fun（s，X） % X=[x1，x2，y1，y2 beta]

global L  %L;%车前后轮距离

beta=X（5）;

V1=[cos（beta）;sin（beta）];%后轮方向

V2=[cos（beta+theta（s））;sin（beta+theta（s））];%前轮方向

T1=V2/cos（theta（s））;   %推導出来的

if abs（beta）<1e-1

T2=1/（L*cos（beta））*（T1（2）-V1（2））;

else

T2=1/（-L*sin（beta））*（T1（1）-V1（1））;

end

f=[V1; T1;T2];

function [Z，X]=funrtoz（RR）

global R L

zhuangju=900;%需要的桩距，调整

R=RR;

L=162;%前后轮中心线切点距离

X=[0;0];% X=[x1，x2，y1，y2 beta]

beta=0;

V1=[cos（beta）;sin（beta）];%后轮方向

Y=X+L*V1;

chuzhi=[X;Y;beta];

sspan=0：0.2：3000;

[s，X]=ode45（@fun，sspan，chuzhi）;

[Mp，t]=max（X（：，2））;

Z=X（t，1）-zhuangju;

function y=theta（s）  %车头拐角

global R  % R 控制轮半径

R1=139.69/2;%后轮半径

r=64.76;%摇杆

%R=24;%控制轮半径，待定

alpha=s/6/R1;

y=asin（R/r*cos（alpha））;%正号向左拐

global L

%L=162;%前后轮中心线切点距离

X=[0;0];% X=[x1，x2，y1，y2 beta]

beta=0;

V1=[cos（beta）;sin（beta）];%后轮方向

Y=X+L*V1;

chuzhi=[X;Y;beta];

sspan=0：0.2：3000;

[s，X]=ode45（@fun，sspan，chuzhi）;

plot（X（：，1），X（：，2），'b'，X（：，3），X（：，4），'r'）;

%z 控制轮半径

global R L

L=162;%前后轮中心线切点距离

[RR，fz]=fzero（@funrtoz，30）;

[fz，X]=funrtoz（RR）;

[Mp，t]=max（X（：，2））;

DS=t*0.2'振幅：'

Mp/2'控制轮半径：'

R=RR

将程序导入软件中，运行并仿真，如图4所示。

通过运行程序，可以绘制出小车运动轨迹图形，结合实际运动情况，综合考虑振幅的大小选择300-400mm，振幅过大，可以有效躲避中间的障碍物，但能量相同的情况下，绕过的障碍物就会减少。同理，振幅减小，绕过障碍物会增加，但会更容易撞到障碍物，所以也要结合实际经验合理优化。仿真运动轨迹如图5所示。

障碍物间距范围从700-1300mm，范围很广，如果全部按照一个参数选择，个别部件尺寸会很极端，调整困难，参考普通车床变数箱工作原理，把一段范围的桩距划分为一组，使用相同的传动比，曲柄变为可调节的几档，这样就可以解决这个问题了。因机构中有齿轮传动，所以传动比为两个整数的比，振幅在一定范围内，这样就得到了这组数据。如表1所示小车参数表。

根据数据表中参数进行加工制作，装配调试，完成小车的设计制作，如图6所示。小车中三档对应的三组传动比，可以绕过不同间距的障碍桩，这个小车经过不断优化，参见了3届全国大学生工程训练比赛，获得三个全一等奖，2019年经过优化已经可以绕过60余个障碍桩，获得国赛特等奖第一名，可见优化设计的重要性。

4  总结

本文通过一个设计案例，论述如何利用Matlab进行机构的参数化设计，并应用于实际设计中。首先通过前期设计，明确基本设计方案，根据方案中各运动部件之间的运动关系，进行数学建模，编写程序。Matlab编写的程序可以方便的对机构中变量进行修改，通过仿真绘图直观地观察运动情况。再结合机构运动情况，确定各结构部件实际尺寸对整体结构运动的影响，最优化选择。理论设计结合实际应用，即不会让设计停留在电脑上的设计图，也不会花很多时间与经费反复的去试做实物验证。灵活合理的使用一个软件工具，可以让设计变得事半功倍，这种方法在参数化设计中有非常高的应用和推广价值。

参考文献：

[1]李京虎，付国强，武斌.两段式仿生扑翼机构设计及仿真分析[J].机床与液压，2020，02（05）：144-148.

[2]冯立艳，耿浩，王文华，梁会硕，蔡敬宇.再现运动规律的曲柄摇杆机构运动与传力性能优化[J].机械设计，2020，3：63-67.

[3]姜森，郝永平，李伦，郭梦辉.基于空间连杆机构实现“8”字形运动的扑翼机的设计[J].机床与液压，2019，47（13）：76-80.

[4]高蕾娜，张钰粮，喻洪平，刘银.平面铰链四杆机构优化问题的建模与求解[J].装备制造与教育，2019，33（03）：24-27.

[5]孙付春，李玉龙.基于MATLAB/GUI的GUSA无级变速器的运动研究[J].机床与液压，2013，41（05）：164-166.

[6]冯慧娟，苗青，樊胜秋，王海龙，王伟.工业机器人机械结构模块化参数化设计[J].机床与液压，2019，47（21）：60-63.