螺纹GFRP筋与混凝土黏结性能试验与理论计算

宋泽鹏, 陆春华, 宣广宇, 蔡启明, 步森壮

(江苏大学 土木工程与力学学院, 江苏 镇江 212013)

在服役环境下,混凝土内部的钢筋由于遭受侵蚀介质的作用而发生锈蚀,导致结构耐久性不足.纤维增强复合材料(FRP)是将纤维材料与基体材料进行复合而制成的高性能材料,因其重度低、抗拉强度高且具有耐腐蚀等优良特性,可成为替代普通钢筋服役于各种侵蚀环境下的理想材料,在土木工程中有着广阔的应用前景[1-2].其中,玻璃纤维增强复合材料(GFRP)筋材就是一种应用较广的FRP筋材.

与钢筋一样,FRP筋与混凝土能否有效协同工作的基础就是两者之间的黏结性能,这也是此类筋材能否在混凝土结构中成功应用的最重要依据[3].因此,GFRP筋与混凝土的黏结性能已成为国内外学者十分关注的课题.由于GFRP筋的生产工艺、表面构造及力学性能与钢筋存在差异,故其与混凝土之间的相互作用和黏结性能也明显不同于钢筋[4].表面处理方式不同时,GFRP筋的黏结性能也有所差异[5-7]：粘砂GFRP筋、加肋GFRP筋和加肋粘砂GFRP筋的黏结强度明显高于表面未经处理的GFRP筋.另外,混凝土强度[8-9]与厚度[10]、筋材直径[11-12]与埋深[13]等都会对GFRP筋的黏结性能产生影响.因此,有必要对不同类型(以表面处理方式和直径为主要因素)GFRP筋与混凝土的黏结性能进行深入研究.

本文选取3种直径的螺纹GFRP筋,制备3组拉拔试件,对比分析筋材直径不同的拉拔试件黏结应力-滑移曲线及其破坏特征.同时,基于弹性力学厚壁圆筒模型,提出螺纹GFRP筋与混凝土黏结强度计算公式,并通过对比各国学者开展的相关试验结果,验证了本文所推导公式的准确性.

1 试验方案

1.1 试验材料

本文采用的3种直径螺纹GFRP筋(G1、G2、G3)均由南京锋晖复合材料有限公司生产,组成为乙烯基酯树脂与玻璃纤维,纤维含量(质量分数,本文涉及的含量等均为质量分数)均为64%.GFRP筋尺寸参数及力学性能见表1.

表1 GFRP筋尺寸参数和力学性能

1.2 试件设计

混凝土设计强度等级为C30,其配合比为m(水泥)∶m(石)∶m(砂)∶m(水)=1.000∶2.838∶

1.274∶0.400,实测28d平均立方体抗压强度fcu为36.94MPa.根据JG/T 406—2013《土木工程用玻璃纤维增强筋》的要求,每种直径的GFRP筋各制备5个标准拉拔试件,如图1所示.其中,混凝土部分的尺寸为150mm×150mm×150mm;黏结区设置在试件中心,黏结区内GFRP筋的有效黏结长度为5d(d为筋材直径),其余部分加设PVC套管.为防止拉拔过程中由于应力集中导致筋材损坏,在加载端处200mm长度内设置钢套管,并使用环氧树脂胶进行锚固.试件养护28d后进行拉拔试验,每组拉拔试件取3个有效试验结果.

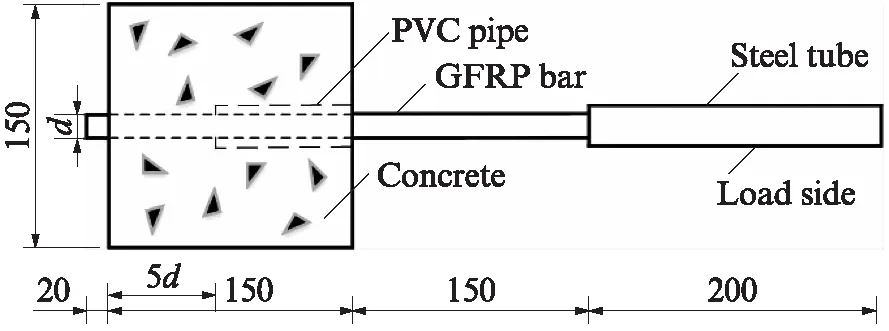
图1 试件示意图Fig.1 Schematic diagram of specimen(size:mm)

1.3 拉拔试验方案

依据JG/T 406—2013,采用UTM5305型电子万能试验机进行拉拔试验.在拉拔试件自由端(预留20mm,见图1)布置精度为0.001mm的位移传感器,加载端放置最大量程为30mm的电子数显百分表,采用位移控制的方式连续加载,速率为1mm/min,直至试件破坏.试验过程中,测量并记录拉拔试件的实时荷载、加载端及自由端位移.

2 试验现象及结果

2.1 破坏形式

与普通钢筋类似,GFRP筋与混凝土之间的黏结力主要来源于3个方面[14]：(1)GFRP筋与混凝土接触面上的胶结力;(2)混凝土握裹GFRP筋而产生的摩阻力;(3)GFRP筋表面肋与混凝土产生的机械咬合力.从拉拔试件的失效结果来看,本文3组拉拔试件的黏结破坏呈现以下2种典型形式[15-16]：

(1)筋材拔出破坏：随着荷载的增大,筋材周围混凝土逐渐产生径向裂缝,在裂缝穿透保护层前,肋间混凝土被压碎,GFRP筋被逐渐拔出,发生筋材拔出破坏.该破坏能够较好地发挥GFRP筋与混凝土的黏结性能,准确反映二者的黏结-滑移全过程,其破坏结果见图2(a).

(2)混凝土劈裂破坏：拉拔过程中,上述径向裂缝迅速开展并穿透保护层,筋材尚未被明显拔出时,混凝土即被完全劈裂导致锚固失效,其破坏结果见图2(b).

图2 试件典型破坏形式Fig.2 Typical damage modes of specimen

试验中,筋材直径8、12mm的拉拔试件主要发生筋材拔出破坏,而直径16mm的拉拔试件均发生混凝土劈裂破坏.这是由于加载过程中,筋材表面横肋对混凝土产生挤压力,其径向应力使混凝土产生环向拉应力;当混凝土保护层厚度与筋材直径之比较大(如直径为8、12mm的筋材)时,所产生的环向拉应力尚未使混凝土完全开裂,GFRP筋表面横肋与混凝土的黏结界面就已发生破坏,相应黏结强度达到最大值,发生筋材拔出破坏[15].当混凝土保护层厚度与筋材直径之比较小(如直径为16mm的筋材)时,所产生的环向拉应力大于混凝土抗拉强度,使整个拉拔试件发生混凝土劈裂破坏;此时,拉拔试件的黏结强度仅与混凝土抗拉强度有关[16].由此可见,随着GFRP筋直径的增大(即混凝土保护层厚度与筋材直径的比值减小),拉拔试件的破坏形式由筋材拔出破坏逐步转变为混凝土劈裂破坏,这与文献[15]的试验结果一致.

2.2 拉拔试件的黏结应力-滑移曲线

拉拔过程中,试件的黏结应力τ可按式(1)计算[10]：

(1)

式中：F为拉拔试件的荷载实测值;d、lemb分别为筋材直径和黏结段长度.

式(1)计算的是筋材沿埋长方向的平均黏结应力,当外荷载达到最大时,对应的黏结应力即为黏结强度τu.此外,本试验中发现拉拔试件自由端滑移存在滞后现象,拟采用加载端位移实测值作sm为其黏结段筋材滑移值.但由于GFRP筋弹性模量较低,在荷载作用下会发生一定的拉伸变形,因此该滑移值应当考虑筋材的拉伸量,这样得到的黏结应力-滑移曲线更加准确.从加载端的位移测试结果来看,GFRP筋的伸长变形包括未黏结段GFRP筋伸长变形和黏结段GFRP筋伸长变形两部分;由于黏结段GFRP筋的周围有黏结力的存在,筋材自身所受的拉力不是很大且不均匀,所以此部分的伸长变形可忽略不计.这里,需要重点考虑未黏结段GFRP筋在拉拔过程中的伸长变形.此时,拉拔试件黏结段实际滑移值s可按式(2)计算[10]：

s=sm-δe

(2)

式中：δe为荷载作用下,未黏结段筋材的伸长量,可按式(3)计算：

(3)

式中：Eg为筋材弹性模量;Ag为筋材横截面面积;l为未黏结段筋材长度,本试验中取l=300-lemb.

根据式(1)～(3),将拉拔试件加载端实际的荷载-位移曲线转化为τ-s曲线,结果如图3所示.

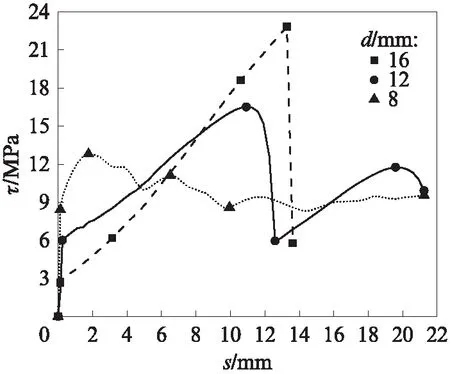
图3 GFRP筋拉拔试件的黏结应力-滑移曲线Fig.3 Bonding stress-slip curves of GFRP bars pullout specimens

由图3可见：3组拉拔试件的τ-s曲线在最初的上升段基本呈线性关系,但之后存在较大差异；筋材直径8mm拉拔试件的τ-s曲线呈来回波动趋势,黏结应力随滑移量的增加基本维持在固定值;筋材直径12mm拉拔试件的黏结应力在上升至最高点后,表现为下降后又上升的双曲线模式;筋材直径16mm 拉拔试件的黏结应力在上升到最高点后迅速下降.

根据图3中3组拉拔试件的τ-s曲线特征,可将该曲线分为4个阶段：

(1)微滑移段：此时GFRP筋与混凝土的黏结力主要来自于二者之间的胶结力,τ-s曲线表现为线弹性,滑移自加载端向自由端传递,但尚未达到自由端.随着GFRP筋直径的增大,筋材表面混凝土的泌水现象逐渐严重,导致混凝土与筋材表面不能充分黏结,二者之间的胶结力降低,因此筋材直径较大的拉拔试件微滑移段黏结应力较小[17].

(2)滑移段：拉拔试件自由端开始发生滑移,表明胶结力退出工作.τ-s曲线呈非线性变化,滑移量增长加快.此时黏结力主要由混凝土握裹GFRP筋产生的摩阻力和筋材表面肋与混凝土产生的机械咬合力提供.拉拔试件加载至接近极限荷载时,其加载端和自由端的滑移加快,裂缝发展至拉拔试件表面,筋材所受径向约束刚度减小,GFRP筋产生较大滑移,黏结应力达到最大值.

(3)下降段：此阶段内黏结应力迅速下降,拉拔试件自由端和加载端的滑移量迅速增加.

(4)残余段：黏结应力保持在一个范围内,波动下降,直至筋材被徐徐拔出.部分拉拔试件因受荷载作用,其筋材表面横肋的尺寸发生变化,导致接触面上混凝土与肋的受压作用不同步,致使拉拔试件自由端附近肋受到的挤压作用逐渐增大,拉拔试件的黏结应力有所回升,此时黏结力主要由摩擦力和部分变形肋的机械咬合力组成.

2.3 黏结强度理论模型

式(1)给出的是实测情况下GFRP筋与混凝土的黏结应力,其考虑因素较为单一,不能从黏结机理上分析两者之间的黏结性能.因此,本文从螺纹GFRP筋的受力破坏机理出发,借助弹性力学中受内压均匀作用的厚壁圆筒模型,研究拉拔荷载下GFRP筋与混凝土的黏结性能,从而建立两者间黏结强度的理论计算模型.GFRP筋与混凝土的厚壁圆筒模型如图4所示,图中e为GFRP筋中心到开裂混凝土边缘的距离;c为混凝土保护层厚度.设GFRP筋与混凝土接触面间的均匀压应力(径向应力)为p;完好混凝土内表面受到的均匀压应力为f.

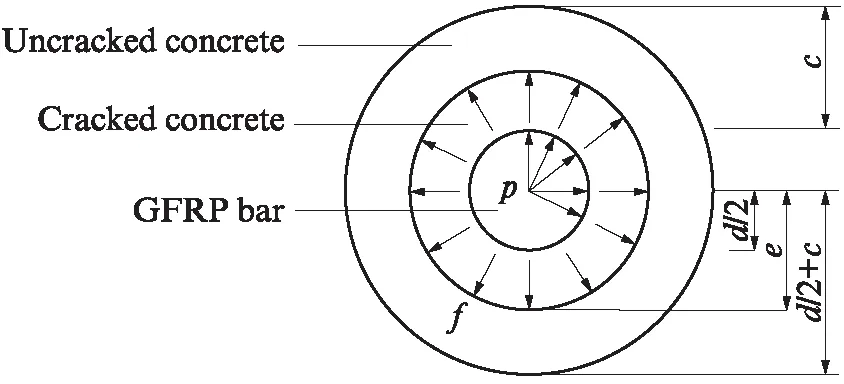
图4 厚壁圆筒模型Fig.4 Thick-walled cylinder model

取螺纹GFRP筋的某个肋及其周围混凝土作为受力分析单元,如图5所示.设GFRP筋与混凝土破坏面的夹角为θ;在破坏面上,GFRP筋对混凝土挤压力为t;设摩擦系数为μ,则黏结摩擦力为μt.将t和μt分解为切向应力和径向应力,切向应力之和为螺纹GFRP筋与混凝土间的黏结应力τ,径向应力之和为压应力p.由弹性力学可知：

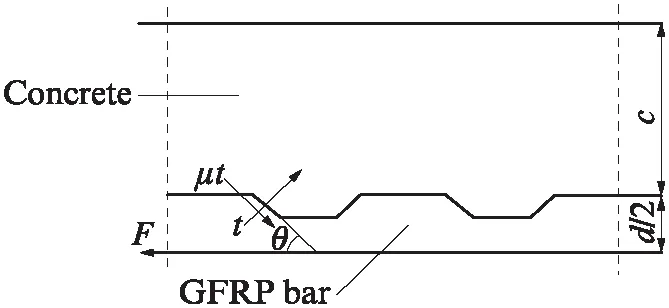
图5 受力分析单元Fig.5 Unit of stress analysis

(4)

p=tcosθ-μtsinθ

(5)

在图4中,根据静力平衡关系,压应力p和f的关系可表示为：

d·πp=2e·πf

(6)

结合式(5)、(6),可得均匀压应力f为：

(7)

未开裂部分混凝土相当于一个均匀受压的厚壁圆筒,由弹性力学可得其环向拉应力σθ为：

(8)

式中：r为试件任一点到试件中心的距离.

在r=e处环向拉应力达到最大值σθmax：

(9)

环向拉应力的最大值即为混凝土抗拉强度：

σθmax=ft

(10)

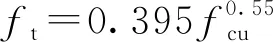
将式(10)代入式(9),并对e求导,可得e的最大值emax为：

emax=0.486(c+d/2)

(11)

联立式(7)～(11),解得对应挤压力t的最大值tmax为:

(12)

将式(12)代入式(4),即得GFRP筋与混凝土的黏结强度τu,c理论计算公式：

(13)

式(13)中，螺纹GFRP筋与混凝土的摩擦系数μ以及两者破坏面夹角θ是2个待定参数.一般认为表面处理方式相同的GFRP筋,其摩擦系数μ也基本相同,基于文献[6]的研究成果,此处μ取为0.5;破坏面夹角θ因筋材直径不同(主要是肋参数不同,见表1)而产生较大差异.一般情况下,螺纹钢筋与混凝土间的黏结破坏面夹角θ为15°～45°,对于本试验所用的螺纹GFRP筋,初步认为其破坏面夹角也在此范围内.然而,需要指出的是,当GFRP筋试件发生劈裂破坏时,由于是混凝土锚固失效导致GFRP筋与混凝土黏结界面尚未破坏即丧失黏结强度[20],故其破坏面夹角可能与GFRP筋的实际黏结性能无关.这里,在探讨螺纹GFRP筋与混凝土黏结破坏面夹角时,姑且假设试件均发生拔出破坏,最后从预测精度上来确定公式的适用条件.为确定不同直径螺纹GFRP筋对应的θ值,从相关文献[8、14-15、21-35]中选取103组螺纹GFRP筋拉拔试件的试验结果(见表2),分别取θ为20°、30°和40°,对比分析式(13)计算得到的理论值τu,c与实测值τu,t的关系,结果如图6所示.

表2 螺纹GFRP筋拉拔试件的黏结强度试验数据

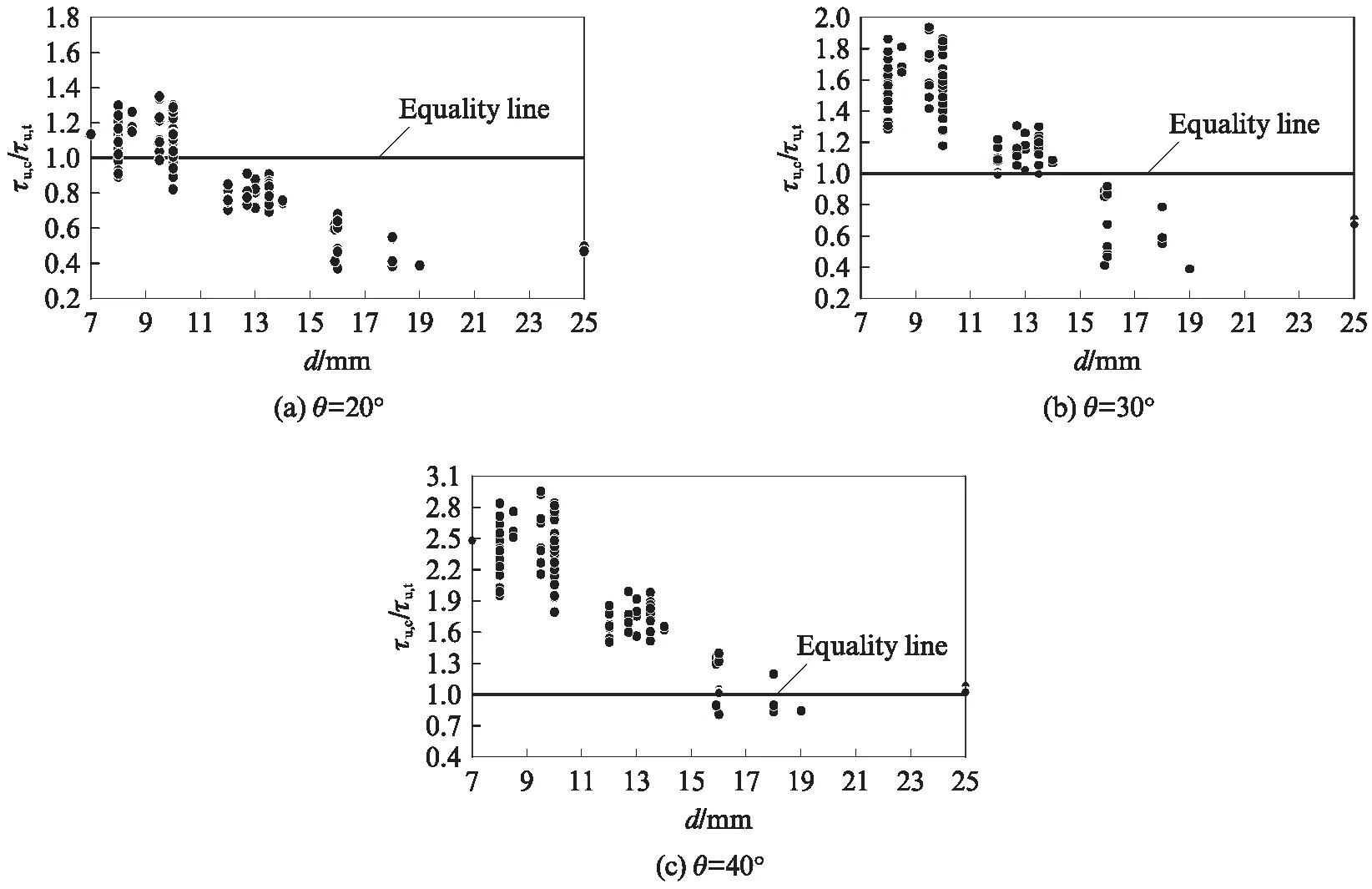
图6 GFRP筋拉拔试件的黏结强度理论值与实测值对比Fig.6 Comparison of theoretical and measured values of bond strength of GFRP bar pullout specimens

图6中,取τu,c/τu,t=1.0作为参考直线,各数据点越靠近参考直线,则表明式(13)越具有准确性.从图6(a)、(b)可以看出,当夹角θ取为20°和30°时,直径7～11mm以及11～15mm GFRP筋拉拔试件的黏结强度理论值与实测值最为接近,故对于该直径范围内的螺纹GFRP筋,其黏结破坏面夹角可分别取为20°和30°.由图6(c)可以看出,直径15mm以上GFRP筋拉拔试件的数据点基本在参考直线的两侧,表明式(13)同样适用于对直径15mm以上螺纹GFRP筋拉拔试件黏结强度的预测,此时黏结破坏面夹角可取为40°.需要指出的是,目前对直径7～15mm螺纹GFRP筋拉拔试件黏结性能的研究较多(见表2),而对直径大于15mm 螺纹GFRP筋拉拔试件黏结性能的研究相对较少,且试验结果存在一定离散性;此外,随着螺纹GFRP筋直径的增大,其拉拔试件易发生劈裂破坏,此时其黏结强度主要取决于混凝土抗拉强度,不能充分发挥两者的黏结性能,导致其黏结强度理论值与实测值存在偏差;上述2个因素导致图6(c) 中数据点具有一定离散性.

2.4 黏结强度实测值与理论值对比

结合本文试验结果以及国内外学者[8,14-15,21-35]的相关试验数据,对螺纹GFRP筋拉拔试件的黏结强度实测值τu,t与模型公式(13)得到的黏结强度理论值τu,c进行对比分析,结果见图7(a).此外,为了进一步验证本文给出的模型公式的准确性,选取文献[24]提出的GFRP筋与混凝土黏结强度计算公式(见式(14))进行同样的预测分析,结果见图7(b).

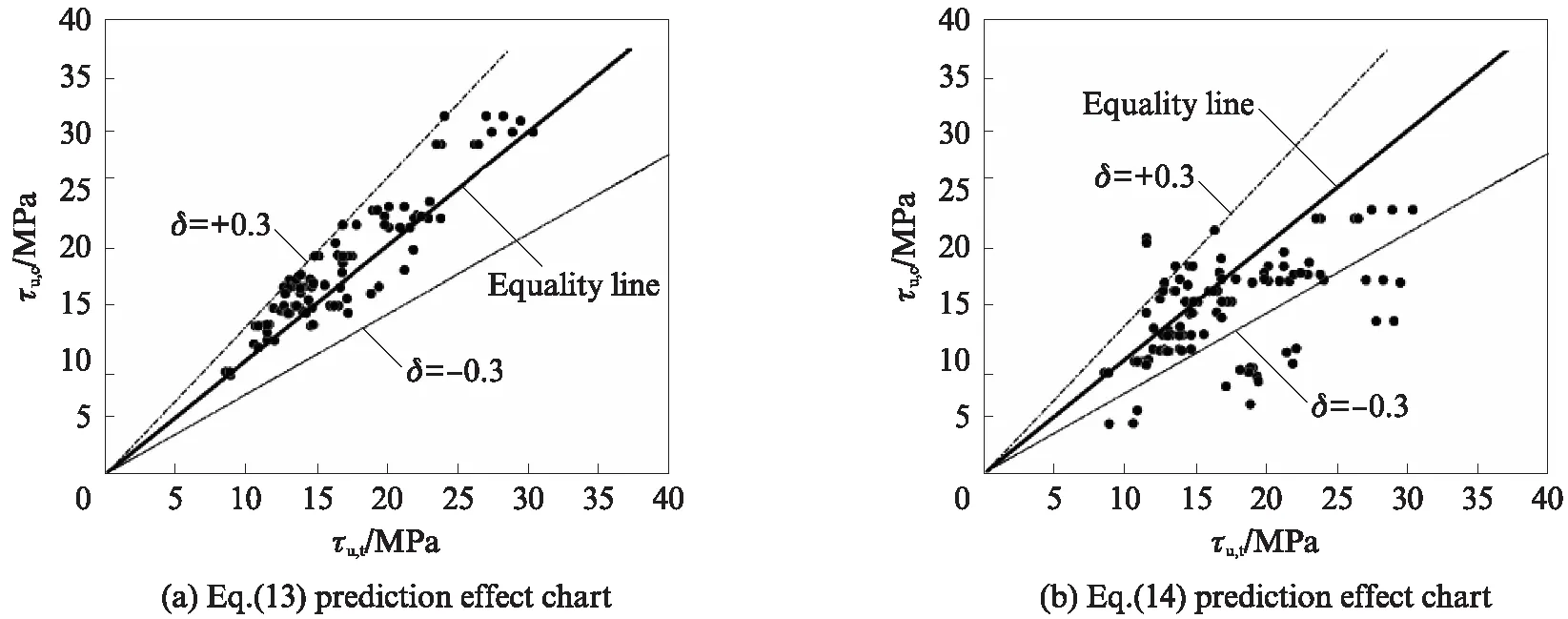
图7 GFRP筋拉拔试件黏结强度实测值与理论值的对比Fig.7 Comparison of measured and theoretical bond strength of GFRP bar pullout specimens

(14)

由图7(a)可知,公式(13)计算所得理论值τu,c与实测值τu,t具有较好的相关性,相对误差δ=±0.3;但随着筋材直径和失效模式的变化,其预测精度也存在一定差异.对于直径较小的GFRP筋(7～15mm)拉拔试件,黏结强度理论值τu,c和实测值τu,t的比值均值为1.086;而对直径较大的GFRP筋(15mm 及以上)拉拔试件,该比值均值为1.186.由此可见,公式(13)对直径较小且发生拔出破坏的螺纹GFRP筋拉拔试件的黏结强度有较好预测精度;对直径较大或发生劈裂破坏的拉拔试件其预测精度略有降低,这一点也与图6(c)中数据离散较大相一致.对比图7(a)、(b)的预测结果来看,本文提出的模型公式(13)较公式(14)具有更好的准确性.因此,在分析螺纹GFRP筋与混凝土的黏结强度时,对于发生拔出破坏的试件,建议采用模型公式(13)进行预测分析.

3 结论

(1)不同直径GFRP筋拉拔试件的破坏模式和黏结应力-滑移曲线在不断变化.当GFRP筋直径较小(8、12mm)时,拉拔试件主要发生筋材拔出破坏,但其黏结应力-滑移曲线存在较大差异.在弹性上升段后,GFRP筋直径8mm的拉拔试件黏结应力-滑移曲线呈来回波动趋势,且黏结应力随着滑移量的增加基本维持在固定值;GFRP筋直径12mm的拉拔试件黏结应力在上升至最高点后,其黏结应力-滑移曲线表现为下降后又上升的双曲线模式;GFRP筋直径较大(16mm)时的拉拔试件在黏结应力上升到最高点时发生劈裂破坏,黏结应力迅速下降.

(2)螺纹GFRP筋的直径显著影响其与混凝土的黏结强度,其黏结强度随着筋材直径的增大而增大.

(3)建立了GFRP筋与混凝土黏结强度的理论计算模型,并通过本文及已有研究结果的对比分析,给出了不同直径螺纹GFRP筋的黏结破坏面夹角θ建议值;对比现有公式,本文给出的螺纹GFRP筋与混凝土黏结强度计算公式具有更好的预测精度,尤其是对于发生筋材拔出破坏情况,其理论值与实测值吻合良好,在此类问题中更具有应用价值.