软土地层中分隔型基坑变形特性及应力路径
李 航,廖少明,2,汤永净,3,申明亮
(1.同济大学土木工程学院,上海 200092;2.同济大学岩土及地下工程教育部重点实验室,上海200092;3.同济大学浙江学院土木工程系,浙江嘉兴 314051;4.上海建工集团股份有限公司总承包部,上海 200080)
随着地下空间的大规模开发和利用,地下开挖对周边环境影响问题日益突出。Tan等[1-2]通过对上海地区多个超大基坑的现场实测数据研究表明,平面尺寸为30 000~50 000 m2的基坑,其围护结构最大侧向变形可达面积小于6 000 m2基坑的3~5倍,对周边环境的影响也更为显著。可见地下开挖所引起的基坑变形和地层运动与基坑尺度(即基坑的开挖深度和平面尺寸)密切相关。在此情形下,常见保护措施,如土体加固、增加围护结构刚度等辅助性方法已无法适应超大深基坑施工的变形控制要求。Tan等[3]对苏州黏土地层中邻近敏感地铁隧道的超大基坑施工案例进行了研究,结果表明采用分区开挖的施工方法并结合常规保护措施可有效控制邻近保护对象侧围护结构的侧向变形。近年来,基于软土地区时空效应理论的基坑分区施工技术和基坑群施工技术已广泛应用于我国上海等软土地区的基坑工程实践中[4-6],成为控制大尺度深基坑变形的有效手段之一。深大基坑在平面上被划分成多个相互关联的子基坑,其中分隔型基坑是基坑群划分的主要形式之一,它将单个基坑划分成紧邻保护对象的狭窄基坑和远离保护对象的较大基坑,常用于基坑附近存在既有历史建筑、地铁隧道等复杂环境。褚峰等[7]利用二维有限元模型研究施工顺序对分隔型基坑变形的影响,验证了小应变硬化土模型(hardening soil model with small-strain stiffness,HSS)在计算模型中的适用性,得到较优的基坑开挖顺序;但其采用简化后的平面应变模型,因此未能有效体现基坑群空间效应和基坑间相互影响,且缺乏定量分析,对工程指导性不强。黄沛等[8]利用二维有限元模型对分隔型基坑开挖顺序和小基坑分区宽度进行了参数分析和优化,但其数值计算结果缺乏实测数据验证。范凡等[9]通过上海航空服务中心工程的实测数据统计分析和数值计算,比较分隔型基坑在控制围护结构变形和地层变形上与常规单个基坑的差异,研究分隔带宽度对紧邻保护对象侧围护结构变形的影响,但未就其变形控制机理作进一步的讨论和分析。
本文依托紧邻敏感历史建筑的上海中心城区超大地下综合体施工案例,建立考虑土体小应变特性的三维有限元数值模型,在将现场实测数据和数值结果进行验证的基础上,以土体应力状态和边界条件动态变化过程为切入点,研究探讨多种影响因素下分隔型基坑变形特性和土体应力路径,以期为类似工程提供理论支撑和工程实践参考。
1 工程概况
1.1 工程背景
本工程位于上海市黄浦区,拟建设成为集办公、商业、酒店及住宅为一体的综合体建筑群,包括两幢高度为300和150 m的超高层建筑和两幢高层建筑,以及深度在14.9~25.6 m的二层至四层地下室。为顺利实施这一项目,需要进行东西向长约500 m,南北向宽约240 m,平面面积约为74 000 m2的超大基坑的开挖(图1)。
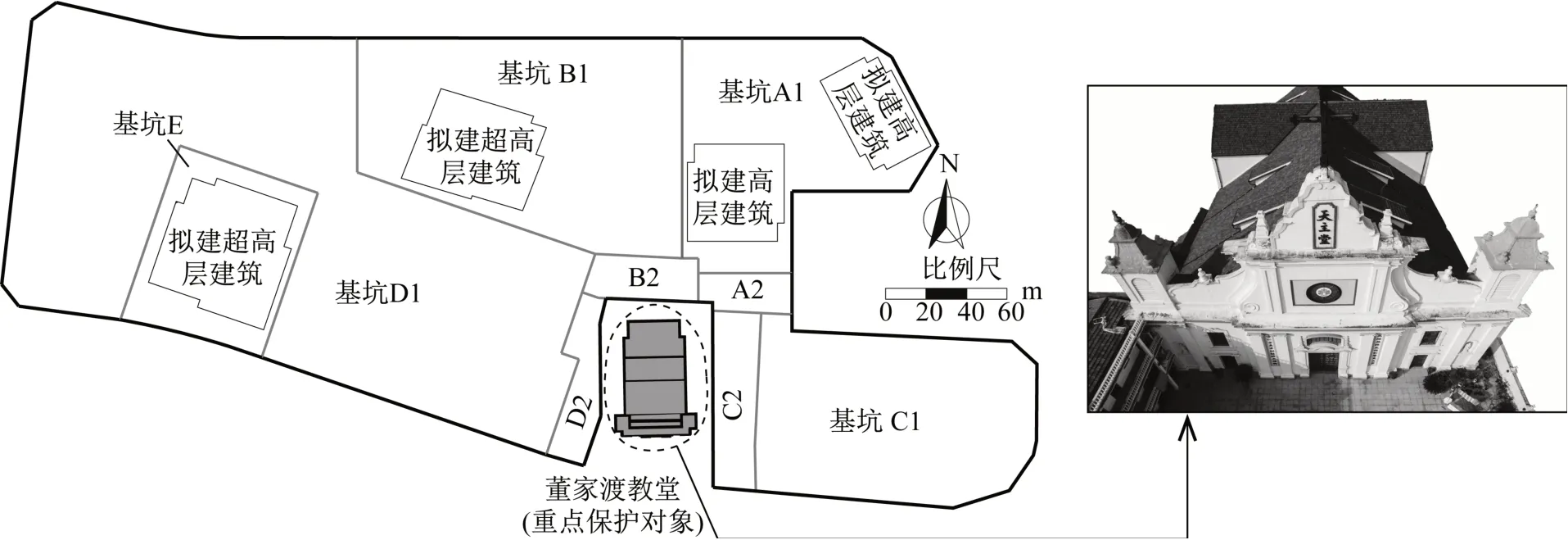
图1 基坑群平面图Fig.1 Plan of foundation pit group
场地内坐落着一处历史保护建筑——董家渡天主教堂,该教堂建成于1853年,为浅基础砖木结构建筑,基础埋深约为0.7 m,结构自重约为1万t。由图1可知,教堂的东西北三面均紧邻基坑,到基坑边缘的距离仅为7.7~12.8 m,可以预见教堂很可能会由于开挖引起的地层运动而产生显著变形,从而导致结构损伤。因此,本项目采用基坑分区施工技术,以减小土体大范围卸荷对教堂及周边环境的不利影响。在基坑群的分区上,教堂东、西、北三面被划分为4组分隔型基坑,分别为基坑A1和A2、B1和B2、C1和C2,以及D1和D2。基坑群的施工顺序如表1所示,先行施工远离教堂的A1和E基坑;在4组分隔型基坑中,先施工小基坑D2和C2基坑,然后施工紧邻大基坑C1;另外两组小基坑A2和B2则在大基坑施工完成后进行开挖。就C1和C2基坑的位置关系,前者位于相对独立的位置,受平行基坑D1和D2开挖影响可能性较大,但由于D2基坑平面尺寸小、D2和C2基坑间距大于2倍开挖深度,且D1基坑最后施工,因此可以推断C2和C1基坑在其开挖阶段受其他基坑影响较小。本文选取位于教堂东侧由基坑C1和基坑C2组成的分隔型基坑为研究对象,其原因为基坑C1和C2共同墙长度最大且形状规则;两个基坑均采用顺作法,在开挖结束后进行支撑拆除,进而完成地下结构回筑,该施工工序在工程实践中更为普遍。
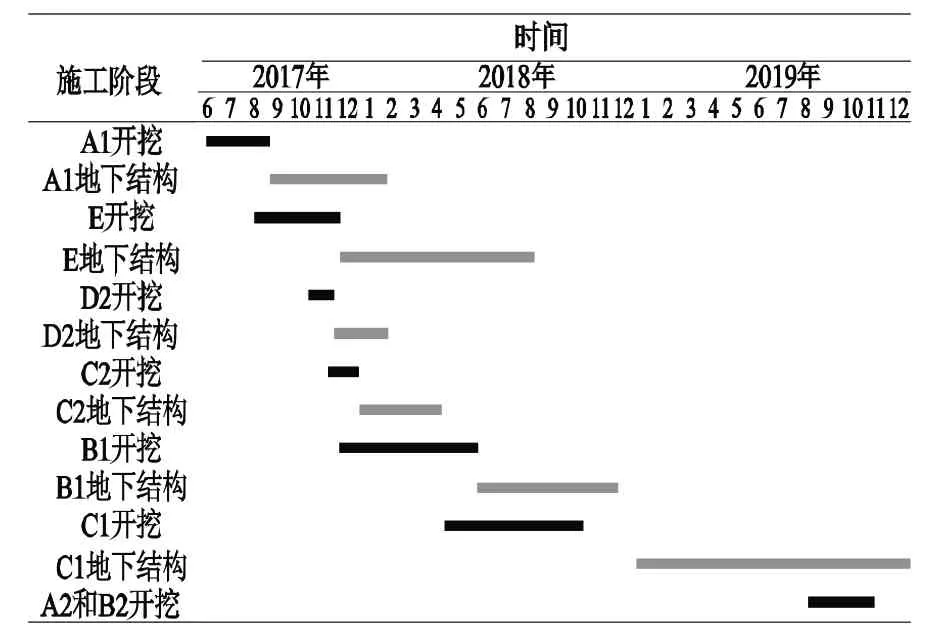
表1 基坑群施工顺序Tab.1 Construction sequence of the foundation pit group
图2a为基坑C1和C2的支护结构平面图,保护对象位于基坑C2左侧。围护结构均采用刚度较大的地下连续墙,紧靠教堂一侧的地下连续墙厚度为1.2 m,其余地下连续墙均为1.0 m。两基坑开挖深度均为18.5 m,地下室层数均为三层。小基坑C2采用一道钢筋混凝土支撑+四道钢支撑,钢支撑采用伺服式系统,自主调控钢支撑预应力;基坑C2分六层土方开挖,开挖结束后施作底板及地下结构。大基坑C1采用四道钢筋混凝土支撑,分五层土方开挖(图2b)。在C1基坑底板浇筑完成并形成一定强度后,进行换撑和拆撑,然后施作地下结构。利用底板和各道楼板作为支撑点,通过临时支撑将作用在围护结构上的水平力传递给底板或楼板,待每层地下结构施作完成并达到一定强度后,拆除临时支撑,直到完成整个地下结构。
1.2 水文地质条件
根据工程地勘报告,场地内地基土体60 m范围内主要由饱和粘性土、粉性土以及砂土组成。基坑C1和C2开挖范围内,分布有①3层、④层、⑤1-1层粘土,其中①3层以粘质粉土为主夹杂淤泥质粉质黏土,该土层渗透性较好,地基承载力相对较高;而第④层淤泥质黏土层和⑤1-1粘土层土性很差,抗剪强度低、压缩性高、呈流塑状,且均属于高灵敏度软土层。场地内各层土体物理力学参数见表2。场地内含水层为浅层的潜水层,水位埋深约为1.5 m;承压含水层位于第⑦层土,其水位不稳定,呈周期性变化,水位埋深均值约为7.0 m,;按照该水位计算,在基坑C1和C2开挖过程中产生突涌的可能性小。
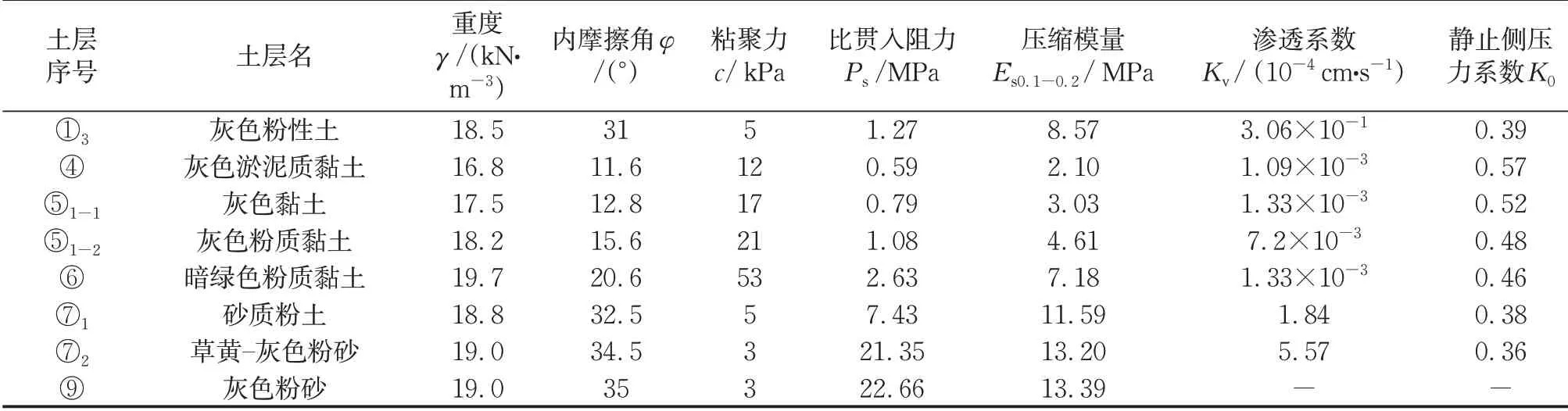
表2 土层基本物理力学参数Tab.2 Basic mechanical parameters of soil layers at the site
2 三维数值计算结果与现场实测数据验证
本节利用岩土有限元分析软件Plaxis3D(v2016),建立三维有限元数值模型,通过现场实测数据与有限元数值计算结果验证数值模型的合理性,为后续进行多工况下的计算和分析奠定基础。土体本构模型采用HSS小应变硬化土模型,该本构模型在敏感环境下的软土基坑数值分析中适用性强[10-11],主要参数包括有效内摩擦角(φ')、有效粘聚力(c')、常规三轴固结排水割线刚度(Eref50)、主固结加载的切线刚度(Erefoed)、卸载及加载弹性模量(Erefur)、与应力水平相关的指数m、破坏比Rf、界面折减系数Rinter,以及小应变参数Gref0和γ0.7,Gref0为小应变刚度试验的参考初始模量,γ0.7为割线剪切模量衰减到初始剪切模量70%时所对应的剪应变。各参数具体含义和取值方法可参见文献[12]和文献[13]。本文HSS模型参数取值参考了文献[10]、[11]和文献[14]中上海地区相关实践经验和试验成果,具体见表3。
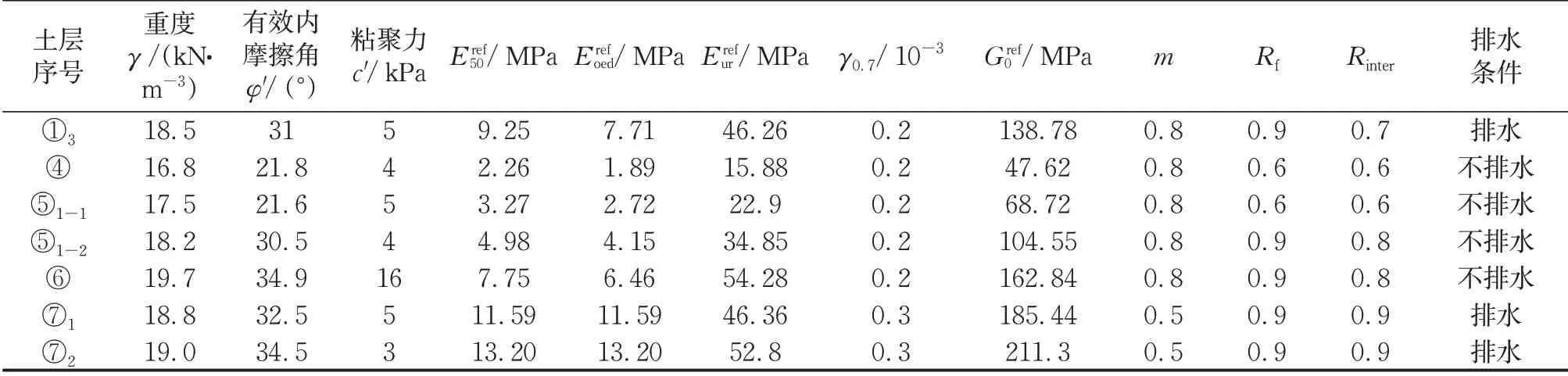
表3 小应变硬化土模型主要参数取值Tab.3 Main parameters of HSSmodel of soil layers at the site
地下连续墙采用线弹性板单元模拟,弹性模量取值为30 GPa;混凝土支撑及围檩采用线弹性梁单元模拟,弹性模量取值为30 GPa,各道混凝土支撑的截面尺寸见图2b;基坑C2中钢支撑直径为609 mm,壁厚为16 mm,采用杆单元模拟。根据基坑开挖影响区域的划分[15-17],为减小模型边界对计算结果的影响,在平面上取基坑边缘到模型边界的尺寸为4倍开挖深度;在深度上基坑坑底到模型底部的距离超过3倍开挖深度。模型尺寸长×宽×高=305 m×242 m×80 m,网格划分如图3所示,在该图中标记了模型典型剖面处位于C2坑内和坑外的分析应力点。数值模型计算工序与现场实际施工一致:地应力平衡→激活地下连续墙→位移清零→基坑C2基坑开挖至-1.8 m→基坑C2第一道混凝土支撑及基坑开挖至-5.8 m→逐层安装钢支撑并施加预应力(-2 300 kN)并开挖至基坑C2坑底→基坑C2地下结构施工→基坑C1开挖至-1.8 m→逐层施作混凝土支撑并开挖至基坑C1坑底。其中C2基坑中钢支撑水平间距为2 m,各道钢支撑预应力控制值为2 300 kN,通过在每个分析步中调整杆单元预应力值可达到开挖阶段钢支撑轴力保持不变的目的。此外,基坑坑内降水将使坑内土体有效应力增加,对土体抗剪强度参数有所影响;在数值计算过程中,本文只考虑坑内土体降水引起的有效应力变化的影响,不对坑内土体强度参数进行调整。

图2 分隔型基坑C1和C2的基本信息Fig.2 General information of divided foundation pit C1 and C2

图3 三维有限元模型网格划分及选取的应力点(单位:m)Fig.3 Mesh of 3D finite element model and the location of selected stress points(unit:m)
选取分隔型基坑C1和C2中L侧(测斜点CX23)、M侧(测斜点CX28)和长边(测斜点TX5-6)地下连续墙的水平位移与实测结果进行比较,测点位置见图2a。图4为按照实际施工顺序计算得到的以上三个测点地下连续墙侧向变形与实测数据曲线,可以看出三维有限元数值计算结果与实测值较为一致。由于小基坑C2采用伺服式预应力钢支撑,在开挖面以上一定范围内的墙体随基坑开挖深度增加产生朝向坑外的变形,呈现“S”型曲线的特点。基于此模型,进行如表4所示多种工况的计算,并对其结果进行比较分析。
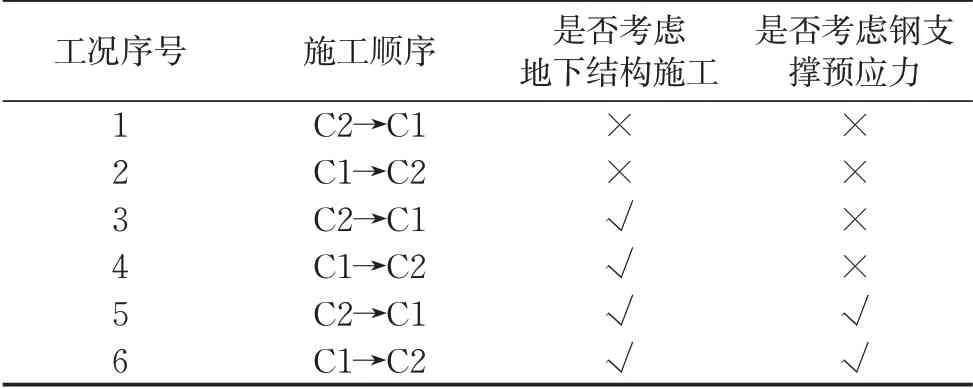
表4 有限元模型计算工况Tab.4 Typical cases of 3D finite element analysis

图4 基于数值计算与实测数据的模型验证Fig.4 Validation of numerical results and measured data
3 计算结果分析和讨论
3.1 开挖顺序对基坑变形及土体应力路径影响
图5为分隔型基坑在不同开挖顺序下,典型剖面处地下连续墙侧向变形(δh)及地表沉降曲线。S为坑外地表到基坑围护结构外边缘的距离,He为基坑最终开挖深度。如图5所示,不同开挖顺序对C2基坑中紧邻保护对象的L侧地连墙和基坑C1和C2共同墙(M侧)的侧向变形有显著影响,而对远端地连墙(R侧)变化不明显。工况2中基坑C1和C2开挖完成时,L墙最大侧向变形δhm为52 mm,较工况1(δhm=60 mm)减小13.3%;地表沉降由49.1 mm减小到44.8 mm,减小幅度为8.6%,因此,在仅考虑基坑开挖顺序时,先开挖大基坑C1,后开挖小基坑C2对于紧邻保护对象侧的墙体变形控制更有利。
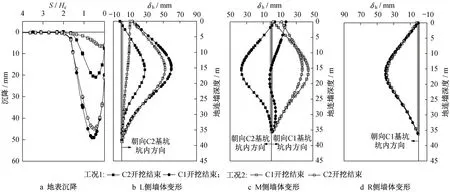
图5 不同施工顺序围护结构变形和地表沉降(工况1和工况2)Fig.5 Wall deflection and surface settlement profile of different construction sequences(Cases1 and 2)
开挖顺序引起的基坑变形差异与土体应力路径和应力状态变化有关。在不同开挖顺序下,土体卸荷方式不同:对于工况1,C2坑内土体先经历C2开挖引起的竖向卸荷,再经历由基坑C1开挖引起的侧向卸荷;与之相反,工况2中C2坑内土体先经历基坑C1引起的侧向卸荷,再经历基坑C2开挖引起的竖向卸荷。图6为不同开挖顺序下,靠近L侧地下连续墙坑外P3点和基坑C2坑底P4与P5点(图3)在p'-q平面上的有效应力路径,横坐标p'为平均有效应力,纵坐标q为偏应力。其中p'=(σ'1+σ'2+σ'3)/3,q=|σ'1-σ'3|,式中σ'1、σ'2、σ'3分别为大主有效应力、中主有效应力和小主有效应力,各主应力为负值时表示受压。整体来看,各应力点的有效应路径以偏应力q变化为主,平均有效应力p'变化不明显。仔细观察可以发现,不同开挖顺序下,坑内、外土体有效应力路径不同。在工况1中,P3点有效应力路径连续经历两次先向上、后向下的动态变化;而在工况2开挖顺序下,P3点有效应力路径在整个开挖过程中先不断朝上而后朝下发展。对于C2坑底土体,在工况1中,P4点有效应力路径在基坑C2开挖阶段先朝下、后朝上,在后续基坑C1开挖阶段,P4点有效应力路径则变化较小;在工况2中C1坑开挖阶段,P4点有效应力路径先向下、后向上;在C2坑开挖阶段,其有效应力路径与前C1坑开挖时类似,但偏应力q变化幅度较大。对于靠近共同墙的P5点,其应力路径既存在与C2坑内土开挖卸荷相同的应力路径,也表现出与坑外P3点相似的应力路径变化特点。可以看出,与普通单个基坑相比,分隔型基坑土体应力路径更为复杂多样。

图6 点P3~P5中有效应力路径(工况1和工况2)Fig.6 Effective stress path at P3 to P5 in Cases 1 and 2
为更好地理解上述各点应力路径,图7a~图7c分别描述了P3~P5点的主有效应力路径和笛卡尔有效应力路径,其中横坐标中σ'x、σ'y和纵坐标中σ'z分别表示笛卡尔坐标系中平面内、外土体侧向应力和竖向应力。以P3点为例(图7a),对于工况1,基坑C2开挖引起坑外土体侧向卸荷,此时平面内水平有效应力σ'x先减小,在开挖最后两层土方时又小幅度增大。其原因是在不排水条件下,墙体水平变形既会引起坑外土体侧向应力释放,也会导致土体产生负的超静孔隙水压力,因此位于坑外与坑底齐平位置的P3点,在基坑C2开挖深度较小时以侧向卸荷为主,此时超静孔隙水压力减小所引起的有效应力增加不足以抵消P3点由于侧向卸荷引起的水平向应力释放;但随着开挖深度增加而接近坑底,由于卸荷引起的负超静孔隙水压力超过侧向卸荷引起的水平应力下降,导致σ'x呈现小幅度增加。随后在基坑C1开挖过程中,P3点有效应力路径与基坑C2开挖时所呈现的应力路径相似,表明P3点受基坑C1开挖影响依然明显,具有多次卸荷效应,故P3点σ'x会经历如上所述的应力变化。对于竖向有效应力σ'z在基坑C2开挖阶段先增大后减小,可解释为在基坑C2开挖深度较小时,σ'z增加主要由负的孔隙水压力引起,但随着开挖深度的增加,该点主应力方向发生小角度偏转,导致σ'z减小。另外,P3点主应力路径与笛卡尔应力路径相似,也即P3点σ'z是大主应力σ'1,而σ'x为小主应力σ'3,这解释了图6中P3在p'-q平面上有效应力路径走向。
对于坑内P4和P5点,其应力路径也有所不同。如图7b和7c,在工况1中基坑C2开挖阶段,由于坑内土体竖向卸荷,P4和P5点竖向有效应力均表现为不断减小的趋势,而由于坑内土体受到墙体侧向变形的挤压,水平有效应力不断增加,此时平面外应力几乎不变,于是水平应力逐渐转变为大主应力,竖向应力变为小主应力,主应力轴随之发生90°偏转,这与P4和P5点主有效应力路径先向下后转而向上以及图6中有效应力路径均吻合。比较工况1和工况2,特征点P3~P5在不同工况下土体应力路径的走向造成土体塑性变形的发展不同,反过来又会影响包括土体刚度等参数,最终表现为围护结构和地层变形差异。

图7 P3~P5点主有效应力和笛卡尔有效应力路径(工况1和工况2)Fig.7 Principle and Cartesian effective stress path at P3 to P5 in Cases 1 and 2
3.2 地下结构施工对基坑变形和应力路径影响
图8 反映了地下结构回筑对分隔型基坑变形性状的影响;图9为L地墙最大侧向变形δhm随施工步序发展情况。比较工况1和工况3可知,当基坑C2开挖结束并完成底板及地下结构后,基坑C1开挖对L墙影响明显减小且最大侧向变形δhm增长速率放缓;基坑开挖全部结束时L墙δhm为36.5 mm,较工况1减小近30%。对于工况4,基坑C1地下结构的施工并未对基坑C2开挖形成有利影响,在基坑C2开挖时L墙最大侧向变形δhm的变化速率与工况2接近;开挖至坑底时,L墙δhm较工况2中有少量增加,为基坑C1地下结构施工和拆撑所致。
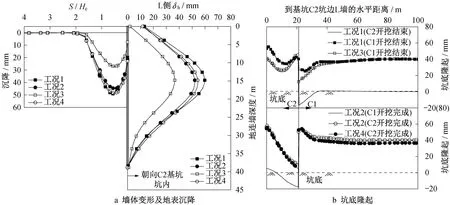
图8 考虑地下结构施工的基坑变形和地表沉降Fig.8 Deformation of foundation pit and surface settlement profile considering construction of underground structures

图9 考虑地下结构施工时围护结构最大侧向变形的发展Fig.9 Maximum wall deflection with excavation depth considering construction of underground structures
通过对比可知,工况3对应的施工工序对紧邻保护对象侧地连墙变形最为有利,而工况4中先期施工的C1基坑地下结构无法对C2基坑,尤其是无法对坑内靠近L墙处的坑底隆起形成有效地抑制作用(图8b)。从P3和P4点的有效应力路径来看,工况3中C2坑内外土体塑性变形发展要小于工况1(图10a)。由于受到底板限制,P4点的偏应力q朝下发展进入弹性区域;而在工况2和工况4条件下,P3点和P4点有效应力路径几乎相同(图10b)。因此,可以看出基坑C2底板及地下结构限制了基坑C2坑底土体的隆起,抑制了坑底土体剪切变形,同时已施工完成的地下结构形成了大刚度结构体,能够进一步限制基坑C1坑内土体卸荷对基坑C2的影响。
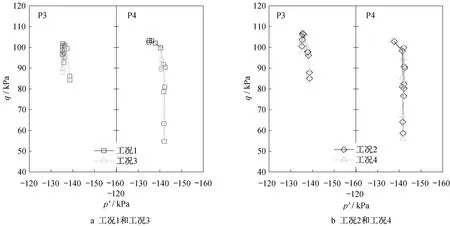
图10 点P3和P4有效应力路径对比(工况1~工况4)Fig.10 Comparison of effective stress path at P3 and P4 in Cases 1 to 4
3.3 钢支撑预应力对基坑变形控制及应力路径影响
在本工程中,狭小基坑C2采用一道混凝土支撑加4道钢支撑的支护体系,在开挖过程中对钢支撑施加预应力并利用伺服式系统进行调整,进一步控制邻近保护对象侧墙体变形。该支护体系常用于邻近敏感建构筑物的地铁车站等狭长型基坑的施工,其效果随地质条件、施工质量、预应力控制等因素而异[18]。图11为考虑伺服式预应力钢支撑时基坑变形和地表沉降计算结果。对于工况5,在基坑C2开挖结束时L墙的侧向变形曲线呈“S”型,并伴随有朝向坑外的变形,这体现了伺服式预应力钢支撑对墙体变形的调控作用;基坑C2和基坑C1开挖至坑底时,δhm分别为9和15.3 mm,分别对应0.05%He和0.08%He。类似地,在工况6中对钢支撑施加与工况5相同的预应力,基坑C2开挖结束时L墙的最大侧向变形δhm为19 mm(0.1%He)。

图11 伺服式预应力钢支撑对围护结构侧向变形和地表沉降的影响Fig.11 Effect of servo prestressed steel supports on wall deflection and ground surface settlement
可见,不论何种施工顺序,对小基坑C2中采用伺服式系统对钢支撑施加合理的预应力,均可显著改善紧靠保护对象侧L墙的侧向变形。但由于工况6中基坑C1先期开挖和地下结构施工的影响,墙体最大侧向变形所处深度及墙顶位移均较工况5大,坑外地表沉降相应增加;最终,工况6地表沉降最大值约为与工况5的2倍。总体来看,工况5和工况6施工过程中都小于相关规范中保护等级为一级(0.14%He[19]和0.18%He[20])时所对应的围护结构水平变形控制要求。
图12为工况3~工况6中P1~P3点在p'-q平面的有效应力路径。
图13 为P1~P3点的笛卡尔和主有效应力路径。将工况3和工况工况5、工况4和工况6进行横向对比,可以发现坑外土体应力路径表现为在基坑浅层土体开挖时,土体水平卸荷引起水平有效应力σ'x减小;在开挖达到一定深度后,在各道伺服式钢支撑的协同作用下,σ'x显著增加。这是由于钢支撑作用在围护结构上的水平推力导致围护结构产生朝向坑外变形(图11),坑外局部土体被水平挤压。当σ'x因过度挤压而超过σ'y时,σ'y变为小主应力,σ'x变为中主应力,最终在p'-q平面的有效应力路径表现为工况5、工况6中偏应力q朝下变化的量值要显著高于工况3和工况4(图12)。可见在伺服式钢支撑轴力作用下,中主应力的变化对土体有效应力路径影响显著。
此外,由于P1应力点位于透水性较好的①3层土,不产生超静孔隙水压力,其有效应力路径与P2、P3明显不同,主要表现为P1点平均有效应力p'的变化范围明显大于P2和P3点。具体来讲,与工况3或工况4相比,工况5和工况6中P1点有效应力路径先朝向左下方运动,而后朝向右下方(图12a和12d)。
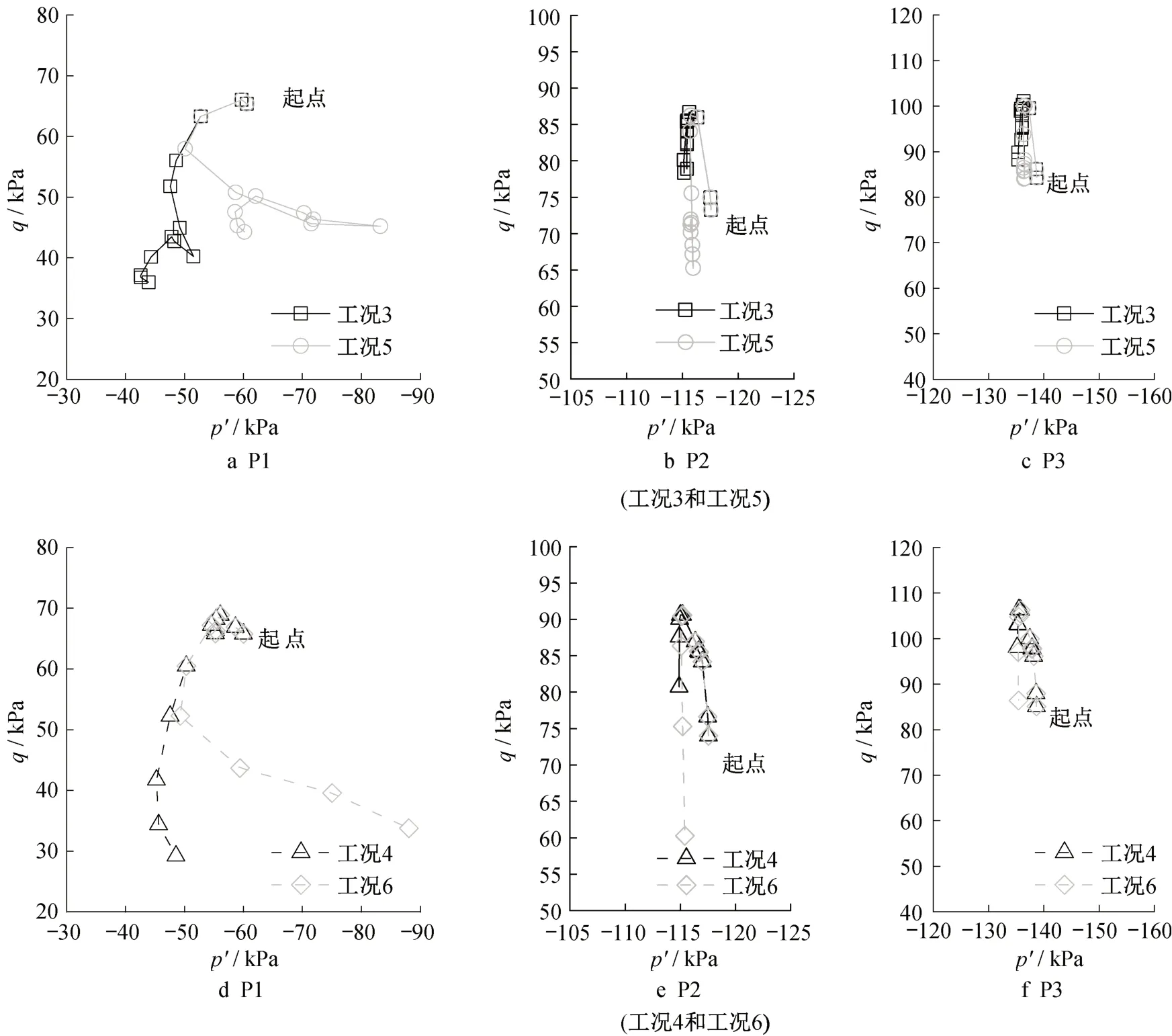
图12 P1~P3点土体有效应力路径(工况3~工况6)Fig.12 Effective stress path at P1 to P3 in Cases 3 to 6
观察图13a中工况5,在C2基坑开挖后,P1点平面内有效应力σ'x和σ'z均减小,这是水平卸荷和应力轴旋转的结果;在C2基坑开挖第四~六层土方过程中,由于各道伺服式钢支撑的作用,σ'x和σ'z均呈上升趋势,且平面外有效应力σ'y也随之增加,在此情形下平均有效应力p'显著增加;在C1基坑开挖过程中,P1又经历一轮水平卸荷,但平均有效应力p'总体上呈逐渐减小的趋势。工况6中P1点应力路径分析与该节中前述工况5分析类似。综上所述,排水条件对土体应力路径起到了不可忽视的作用。

图13 P1~P3点主有效应力和笛卡尔有效应力路径(工况3~工况6)Fig.13 Principle and Cartesian effective stress path at P1 to P3 in Cases 3 to 6
4 结论
本文通过三维有限元数值模型计算分析和实测数据相结合,探讨了不同因素影响下的分隔型基坑变形特性及土体有效应力路径,得到以下几点结论和建议:
(1)受土体卸荷应力路径和边界条件的影响,分隔型基坑的开挖顺序和地下结构的回筑对分隔型基坑变形特性有显著影响,而仅靠优化基坑开挖顺序来达到控制基坑变形目的,其作用有限且不全面。
(2)仅考虑基坑开挖时,先施工大基坑,再施工小基坑的开挖顺序对紧邻保护对象侧的墙体侧向变形控制更为有利,较“先大后小”的开挖顺序,墙体侧向变形和地表沉降分别降低13%和9%。在不同开挖顺序下,坑外土体有效应力路径呈现同一模式的往复变化特点,坑底附近土体则表现出不同应力路径模式,其原因在于分隔型基坑先后施工所产生的多次卸荷效应和不同施工顺序导致的卸荷方式差异。
(3)当考虑基坑地下结构回筑时,先开挖小基坑,然后施作其地下结构,最后施工大基坑为最优方案,其综合效果较仅考虑开挖顺序时所得到的结果显著提高,较不利工况围护结构侧向变形降低30%。
(4)采用伺服式预应力钢支撑能够有效控制分隔型基坑墙体侧向变形;在开挖较深层土体时,各道伺服式钢支撑协同作用使得围护结构产生朝向坑外水平位移,坑外土体先水平卸荷后挤压,抑制了坑外土体塑性变形发展。多种计算工况结果表明,在伺服式钢支撑控制作用下,可将保护对象侧围护结构变形控制在0.1%He范围内,适用于对围护结构变形控制极为严格的复杂环境。
作者贡献说明:
李航:搜集整理实测数据,建模和数据分析,论文撰写和返修。
廖少明:总体思路和研究方法把控,论文审阅和修改。
汤永净:论文审阅、修改和润色。
申明亮:协助进行现场调研,提供相关资料和数据。

