后结合预应力组合梁桥的混凝土预应力实效测试与分析

苏庆田，邹迪升，张龙伟，陶仙玲，黄 超

（1.同济大学土木工程学院，上海 200092；2.台州市交通勘察设计院有限公司，浙江台州 318000；3.台州高速公路建设指挥部，浙江台州 317000；4.杭州市市政工程集团有限公司，浙江杭州 310006）

钢混组合梁桥是一种通过剪力连接件将钢梁和混凝土桥面板结合成一体，并共同承担作用的梁式桥。在正弯矩作用下组合梁桥中的钢材和混凝土优势互补，材料各自的力学性能得到了充分的发挥，但是在负弯矩作用下容易出现钢梁受压失稳和混凝土桥面板受拉开裂［1］。目前大跨径连续钢混组合梁桥成为实际工程中跨越线路和路口位置处比较合理的结构形式。连续组合梁桥最突出的问题是负弯矩区混凝土桥面板受拉开裂，从而降低其使用性能和耐久性能［2］。

提高负弯矩区桥面板抗裂性能的方法一般可归纳于三类：第一类是减少混凝土桥面板在使用过程中承担的拉应力，常用的方法有在负弯矩区钢梁底板上浇筑混凝土［3］、降低负弯矩区钢梁与混凝土桥面板之间连接程度［4］、改变全桥混凝土桥面板浇筑顺序［5］等；第二类是增加桥面板内的预压应力储备，常用的方法有常规预应力法［6］、调整中支点高度法［7］以及预加荷载法等；第三类是提高混凝土材料自身的抗力，选择抗拉性能更好的混凝土材料［8］。

上述方法在工程中均有使用，其中预应力法使用较为广泛。但是在钢梁与混凝土板形成组合截面后再施加预应力，会把预应力也施加到钢梁上。特别是随着桥梁跨度的增大，钢梁在组合截面中所占刚度比例在增加，导致常规预应力方法的混凝土预应力效率降低。文献［9］提出了后结合预应力方法，在混凝土板和钢梁没有形成组合截面之前仅对混凝土板施加预应力。为了研究后结合预应力组合梁负弯矩区的力学性能，刘思维［10］、郭瑞［11］、陈德宝［12］等开展了模型加载试验，证明后结合预应力组合梁可以有效提高负弯矩区混凝土桥面板的开裂荷载，并限制裂缝的出现和发展。胡一鸣［13］采用数值方法对后结合大跨径连续组合梁桥进行了不同跨径组合梁桥的截面尺寸优化。目前，基于后结合预应力法的研究仅局限于数值分析和模型试验，还未对实际桥梁的运用效果进行测试评估，也没有分析比较后结合法的适用范围。鉴于后结合预应力法开始在工程中运用，非常有必要结合实际工程的现场测试检验后结合预应力方法的效果，并对理论方法进行校验。因此本文首先基于换算截面法推导了后结合法和常规预应力法的中支点截面应力计算公式，然后对国内首次采用后结合预应力法的大跨度组合梁桥进行实桥实测，对比分析后结合预应力法和常规预应力法在组合梁负弯矩区产生的预压应力效果，进一步对不同跨径连续组合梁桥的后结合桥面板提出合理的配束方案，为以后的组合梁桥设计提供参考依据。

1 后结合预应力法的理论效果

为了分析后结合预应力法的理论效果，分别计算后结合预应力组合梁和常规预应力组合梁负弯矩区截面的受力状态。简化的截面计算图示如图1所示，图中A、E和I分别代表面积、弹性模量和惯性矩，对应下标s、c、r、p和o分别代表钢梁、混凝土板、普通钢筋、预应力钢筋和组合截面，钢梁和混凝土板的高度分别为hs和hc，各部分形心到钢梁上顶缘的距离为y。通过换算截面法［14］计算钢梁和混凝土的应力，采用如下基本假定：①组合梁中钢梁和混凝土之间的滑移忽略不计，②钢混组合截面的变形符合平截面假定，③截面在使用过程中处于线弹性状态，应力状态可以线性叠加，④不考虑群钉孔对桥面板的削弱作用。

在后结合预应力组合梁桥的施工和使用过程中，中支点截面的受力状态可分为三个阶段，如图2所示，设钢梁和混凝土桥面板作用于中支点截面的一期恒载弯矩为M1，二期恒载和使用荷载作用于中支点截面的弯矩为M2。

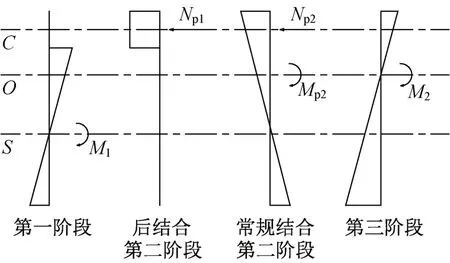
图2 各阶段荷载作用下的组合梁中支点全截面弹性应变分布Fig.2 Elastic section strain distribution at the intermediate support of composite beam under each construction stage

图中第一阶段仅由钢梁承担一期恒载产生的内力；第二阶段仅由混凝土桥面板承担预应力钢束产生的内力，可将施加的后结合有效预应力Np1视为外荷载直接作用于混凝土板；第三阶段由钢混组合截面共同承担二期恒载和使用荷载产生的内力。由上述受力过程可以推导出后结合组合梁中支点截面处钢梁上缘应力σPst，钢梁下缘应力σPsb和混凝土桥面板上表面应力σPct。其中压应力为正、拉应力为负，上标括号内的数字代表受力阶段编号。

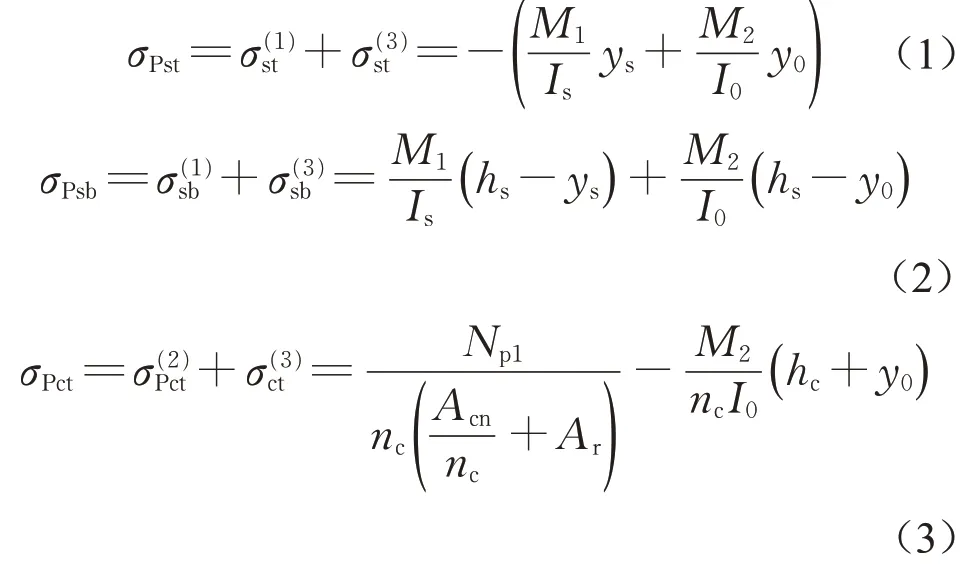
式中：nc为弹性模量比，nc=EsEc；Acn为扣除预应力管道面积的混凝土净截面面积。

常规预应力组合梁在张拉预应力前，混凝土板就已经和钢梁结合在一起。在第二阶段中可将施加的常规结合有效预应力Np2视为外荷载作用于组合截面，同时要考虑预应力次效应在中支点截面处产生的赘余弯矩Mp2。常规预应力组合梁中支点截面处钢梁上缘应力σNst，钢梁下缘应力σNsb和混凝土桥面板上表面应力σNct可按照式（4）～（6）计算。

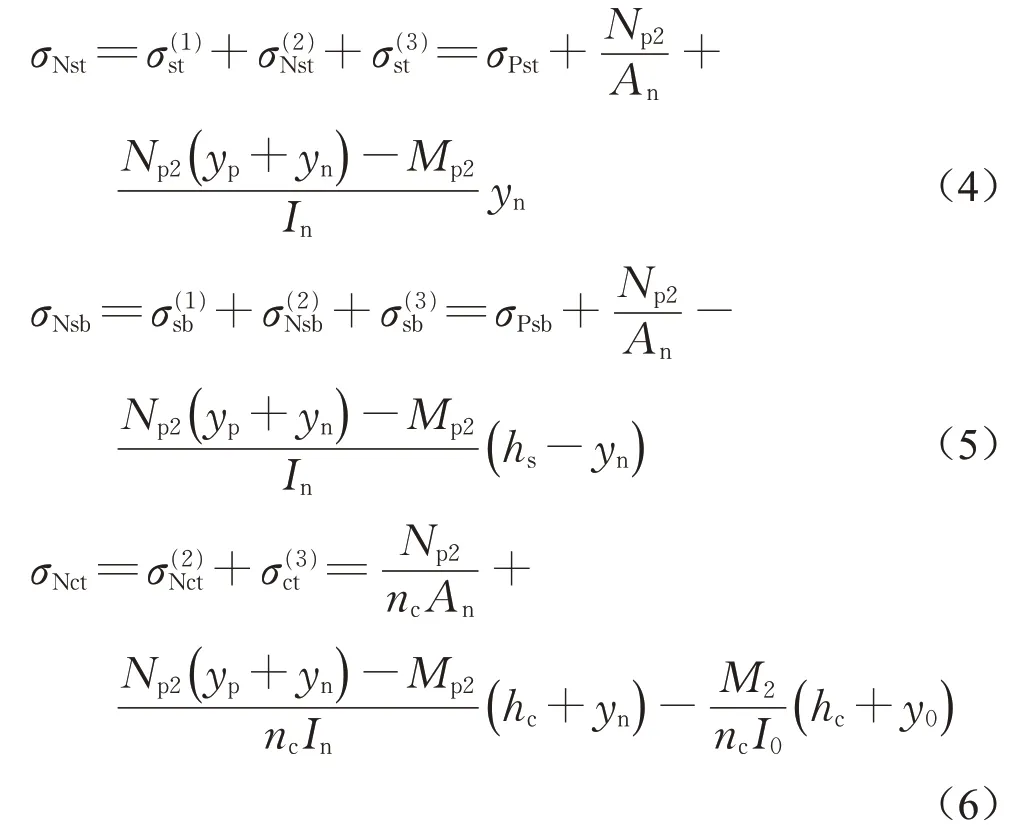
式中：An，In为换算组合截面的几何特性，其中混凝土采用扣除预应力管道面积的净截面计算；yn为换算组合净截面形心到钢梁上顶缘的距离。

从式（4）～（5）可以看出，常规预应力组合梁中的钢梁应力比后结合多出一项，该项应力是由第二阶段的有效预应力Np2和赘余弯矩Mp2共同作用于组合截面中产生的。从式（3）、式（6）可以看出，混凝土板上表面应力σPct和σNct的区别仅体现于两者分别获得不同的预压应力σ(2)Pct和σ(2)Nct。常规预应力组合梁存在由预应力次效应产生的赘余弯矩Mp2，该弯矩在混凝土桥面板的上表面产生拉应力，一定程度上降低了预应力张拉效果。

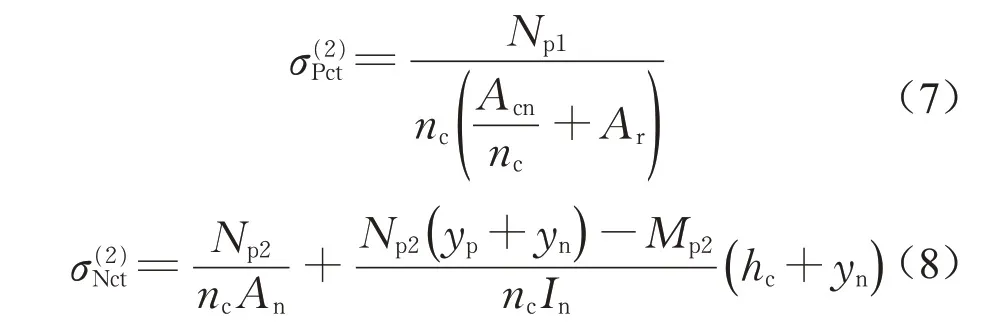
为了定量比较后结合预应力法的理论效果，以浙江省台州市一跨径为36 m+60 m+36 m大跨度组合梁为背景工程，取6个组合箱梁中一根主梁进行简化，简化的中支点截面如图3所示。为了计算常规结合中的赘余弯矩Mp2，将三跨连续梁简化成半结构计算（图4）。

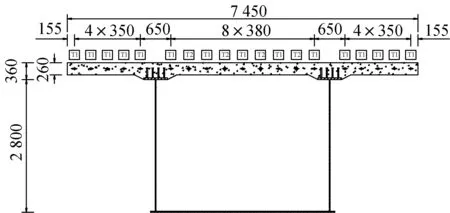
图3 实桥中支点截面的简化图示（单位：mm）Fig.3 Simplified diagram of intermediate support section of the bridge(unit:mm)

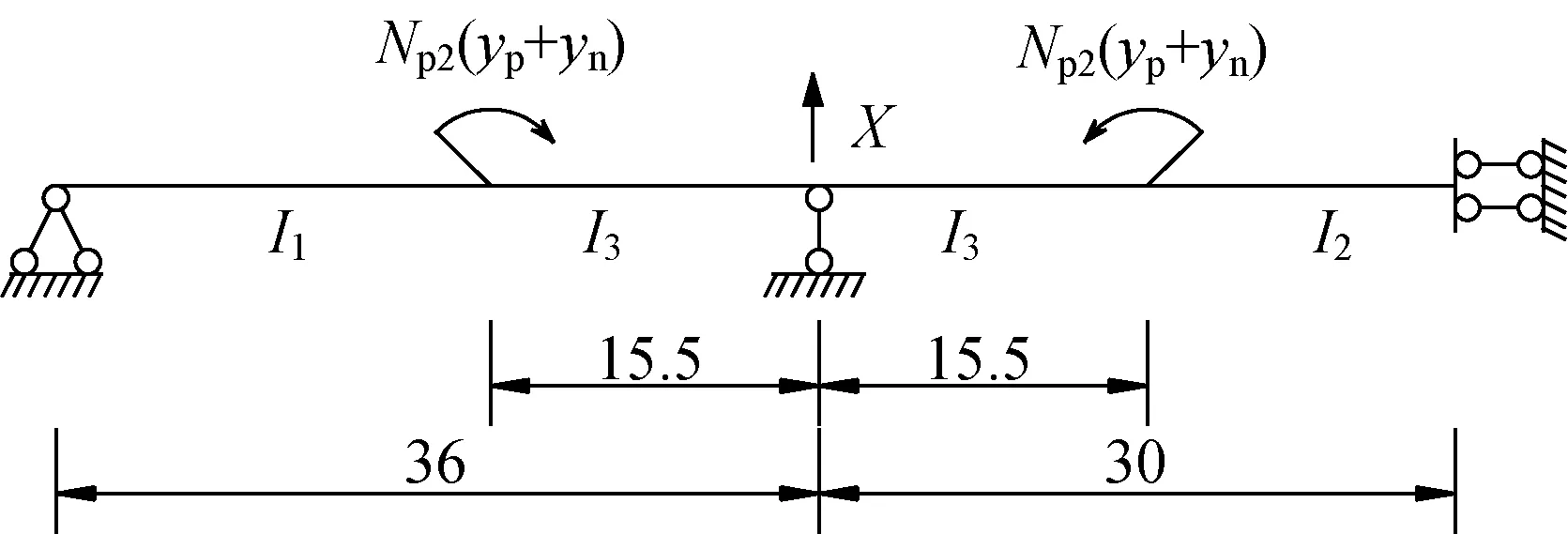
图4 常规预应力法的实桥半结构力学模型（单位：m）Fig.4 Half structure mechanical model of real bridge based on the conventional prestressing method(unit:m)

后结合的桥面板有效预压应力σ(2)Pct只取决于桥面板的构造形式。已知桥面板纵向普通钢筋的直径为16 mm，间距100 mm双层布置。预应力钢绞线的直径为15.2 mm，共103根，预应力张拉控制应力为1 534 MPa。假设考虑短期预应力损失度为17%［14］，预应力全部作用于混凝土形心处。将以上参数代入式（7）计算可得σ(2)Pct为8.86 MPa。

常规结合的桥面板有效预压应力σ(2)Nct取决于组合截面的几何特性，以及结构产生的次效应。根据力法原理，令中支点反力为赘余力X，列出力法方程式（9）～（11）。

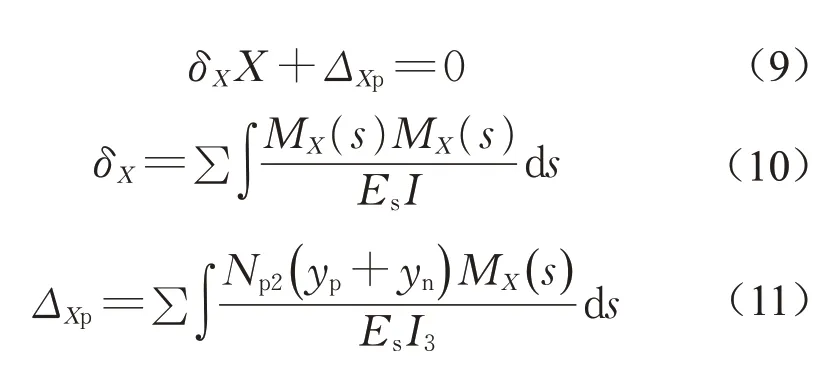
按《公路钢混组合桥梁设计与施工规范》（JTG D64-01—2015）［15］第5.3.2条考虑剪力滞效应的影响，边跨惯性矩I1、主跨惯性矩I2和负弯矩区惯性矩I3分别为0.320、0.430和0.842 m4。假设考虑17%的短期预应力损失，Np2的值与Np1的值相同，则求解出赘余反力X和赘余弯矩MX分别为193 kN和6 961 kN.m，预应力次效应占主效应的15.51%。将以上参数代入式（8）计算可得σ(2)Nct为6.77 MPa。

综上计算结果表明，相比于常规预应力法，后结合预应力法显著提高了预应力张拉效率。对于本背景工程中的组合梁，后结合桥面板上表面获得的预压应力比常规结合桥面板增加了30.9%。值得关注的是常规结合桥面板的预压应力沿着高度方向递减分布，混凝土板底面的预压应力更小，而后结合桥面板在混凝土全截面都能维持相同的预压应力水平。

2 后结合预应力组合梁桥的现场实测效果

2.1 工程概述

本文背景工程为浙江省台金高速东延台州市区连接线36 m+60 m+36 m连续槽形钢-混凝土组合梁桥，桥面板宽度为44 m，横向由6个箱室构成。主梁负弯矩区采用变高度截面，总梁高从2.35 m均匀变化成3.22 m，桥面板一般厚度为260 mm，加腋处厚度为360 mm。本工程为了提高负弯矩区混凝土桥面板在使用过程中的抗裂性能，采用后结合预应力法增加桥面板的预压应力储备。施工中的关键步骤如表1所示。

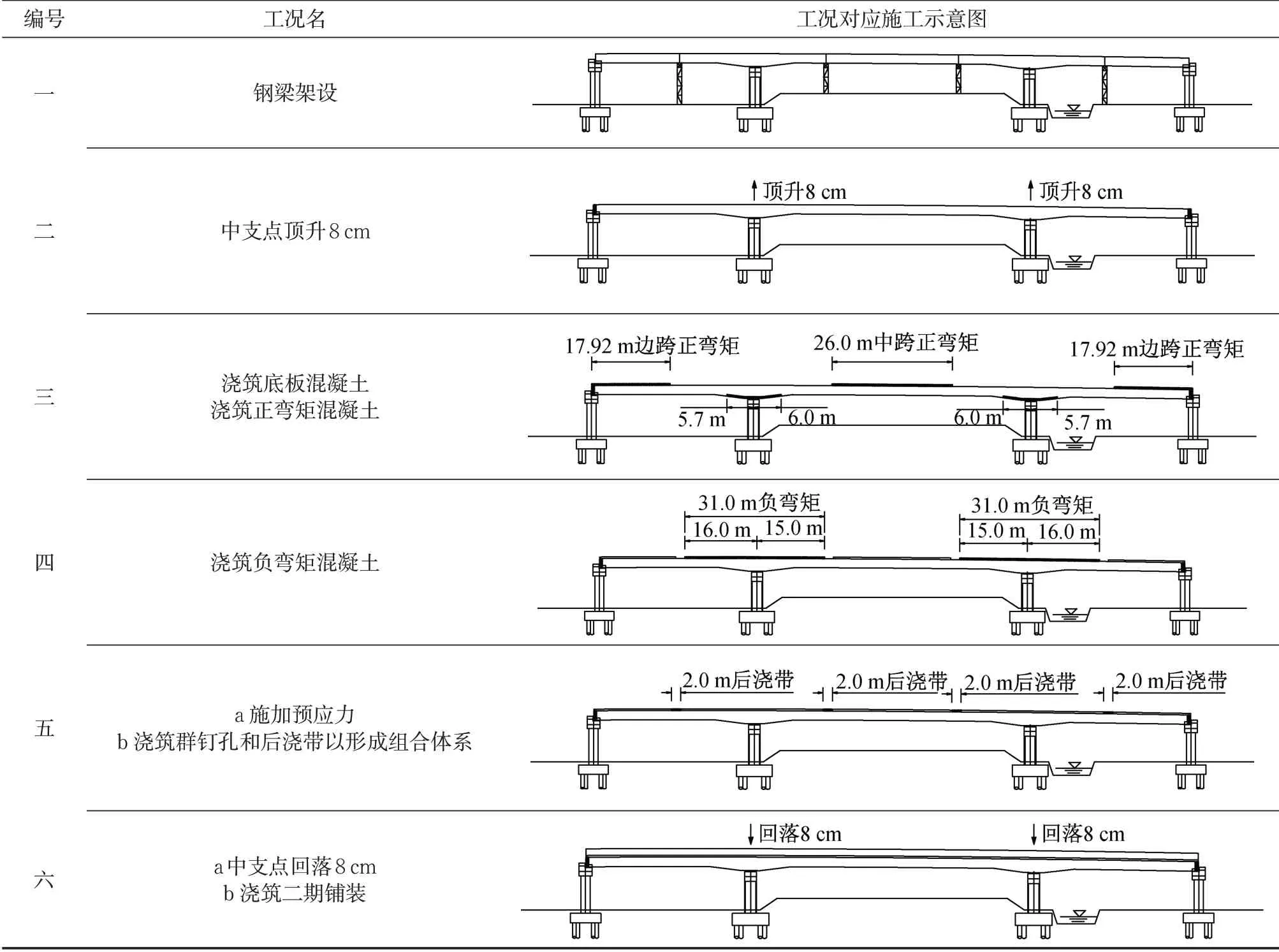
表1 后结合预应力组合梁施工关键步骤Tab.1 Critical construction stage of the post-combined prestressing composite bridge

背景工程在主梁负弯矩区采用了带钢套箱的新型群钉连接构造（图5和图6）以实现后结合预应力技术，在钢梁上翼缘顶部铺设油毛毡隔离钢梁与混凝土，放置钢套箱并制作钢筋网。钢套箱的尺寸为450 mm×550 mm×330 mm，套在4×5布局的群钉外作为浇筑混凝土的群钉孔内模，防止混凝土在浇筑过程中和焊钉根部连为一体。张拉完预应力钢束后，在钢套箱内浇筑自密实高强砂浆，从而形成组合体系共同受力。

图5 钢套箱群钉构造Fig.5 Group studs with steel casing

图6 浇筑负弯矩桥面板Fig.6 Casting of negative moment zone

2.2 测试方案

为了检测后结合预应力法在实际桥梁中的使用效果，本工程在负弯矩区中支点截面布置了若干应变测点测量各施工阶段中钢主梁和混凝土桥面板的应力。选取南侧中支点靠边的三个箱室作为应力测试截面，截面的应变计编号如图7b所示。图中，C、T、L分别代表混凝土桥面板、钢梁上翼缘、钢梁底板的应变计测点。

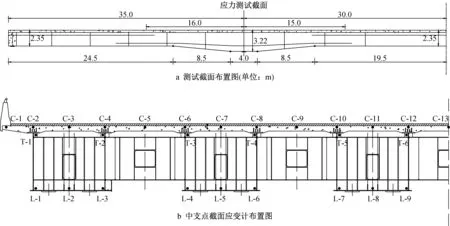
图7 测点布置图Fig.7 Configuration of field test positions

2.3 钢梁应力测试结果

将实桥中测得的同一箱室的钢梁上翼缘应力和底板应力分别取平均值，随着施工的不断进行，应力平均值的变化如图8、图9所示。同时建立全桥的板壳实体有限元模型，并分析施工过程中钢梁的受力状况，提取测点位置处的计算结果。从图8中可以看出，不同箱室上翼缘的实测结果反映出了相同的变化规律，钢梁上翼缘的应力在前4个工况中增长显著，而在张拉预应力过程基本没有发生变化。从图9中可以看出，在预应力张拉过程中钢梁底板的应力几乎没有发生变化。以上测试结果表明实桥中采用后结合预应力方法不会把预应力转移到钢梁上。

图8 中支点钢梁上翼缘应力测试结果Fig.8 Measured stress in the steel top flange of the intermediate support

图9 中支点钢梁底板应力测试结果Fig.9 Measured stress in the steel bottom plate of the intermediate support

2.4 混凝土应力测试结果

负弯矩区混凝土桥面板的预压应力储备主要来自于张拉预应力钢束。图10为张拉预应力钢束后桥面板实测预压应力的横向分布图，总体规律为靠近内护栏箱室的混凝土应力大于靠近边护栏箱室。位于钢梁上翼缘之间的混凝土桥面板平均获得10.49 MPa的预压应力，位于钢梁上翼缘顶部的混凝土桥面板仅平均获得1.76 MPa的预压应力，两者相差近6.0倍。该现象说明群钉孔构造削弱了桥面板的整体性，预压应力无法传递到纵向两个群钉孔之间的混凝土中。为了评价后结合桥面板在张拉钢束后平均获得的预压应力，将桥面板横截面按图11编号，并划分成两种区域，有群钉孔的区域为低预压应力区，无群钉孔的区域为高预压应力区。按面积比例得到每个区域的测试权重，采用式（12）得到测试结果的加权平均值为9.14 MPa，与第1节的理论计算结果8.86 MPa比较接近，说明第1节的理论计算方法可以较好地预测后结合预应力的实施效果。

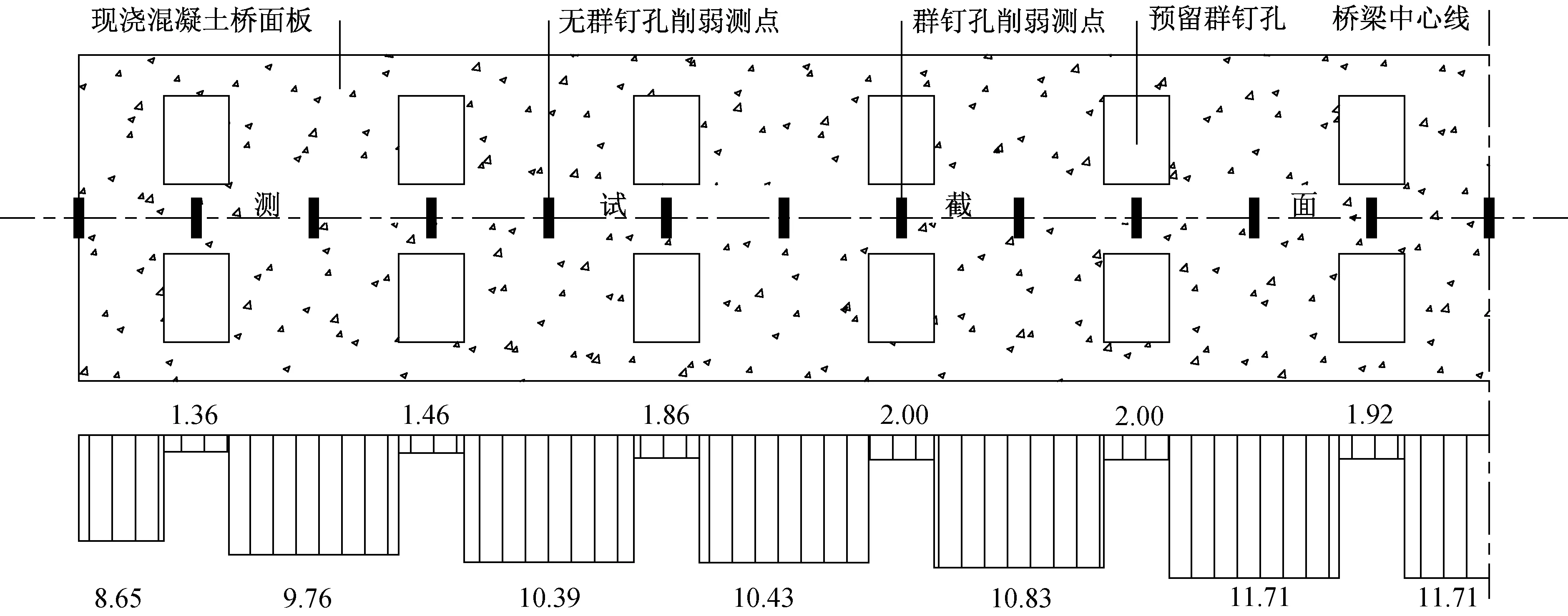
图10 张拉预应力钢束后桥面板实测预压应力横向分布图（单位：MPa）Fig.10 Transverse distribution of the pre-compression stress measured in the bridge deck after prestressing(unit：MPa)

图11 后结合桥面板平均预压应力计算示意图Fig.11 Calculation diagram of mean pre-compression stress in the post-combined deck

同时采用全桥的板壳实体有限元模型，计算了混凝土桥面板在张拉预应力时的应力分布。各测点预压应力的平均值为10.15 MPa，与实测值相差11%。主要是在有限元模型中忽略普通钢筋、群钉孔和预应力管道的影响及测试误差造成的。此外，采用有限元方法分析常规预应力法在桥面板内产生的预压应力，各测点应力的平均值为7.65 MPa。将有限元和理论计算结果汇总于表2，可以看出：相较于常规预应力法，本背景工程采用后结合预应力法可以使桥面板的预压应力提升30%，后结合预应力法相比于常规预应力方法具有更高的预应力施加效率。

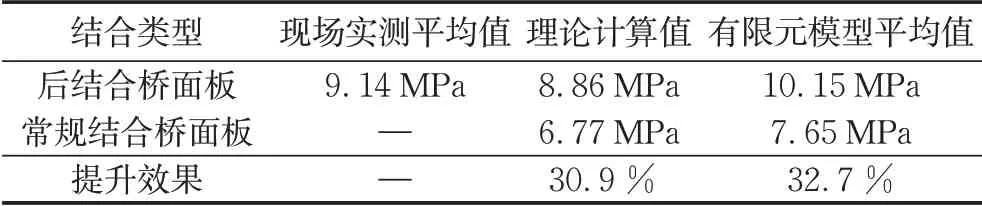
表2 张拉预应力钢束后后结合和常规结合桥面板预压应力比较Tab.2 Comparison of pre-compression stress in the post-combined deck and the conventional pre-combined deck after prestressing

3 后结合预应力法和常规预应力法比较分析

为了更广泛地比较后结合预应力法和常规预应力法在负弯矩区桥面板内产生的预压应力效果，基于文献［13］中优化的中大跨径（主跨40～120 m）后结合预应力连续槽型钢箱组合梁桥进行简化分析。按照常见的高速公路双向四车道布置，单个槽型箱室对应的混凝土板宽度为6 800 mm，厚度随跨径从260 mm增加至300 mm。

在主跨40～70 m的后结合预应力组合梁中，桥面板可以按照全预应力方案进行配束，然而对于主跨70 m以上的组合梁桥面板，由于受到尺寸限制，在考虑构造因素的情况下最多只能布置125根预应力钢束。假设预应力张拉控制应力为1 534 MPa，短期预应力损失为17%，预应力全部作用于混凝土形心处。分别按照式（7）和式（8）计算后结合预应力法和常规预应力法在桥面板上表面产生的预压应力储备，计算结果如图12所示。从图中可以看出，主跨跨径从40 m增加到120 m，相比常规预应力方法，后结合方法桥面板的预应力提升效率从11%增加到52%。后结合桥面板获得的预压应力只取决于桥面板的尺寸和预应力配束方案，预压应力水平在主跨70 m以下随钢束的增加而变大，在主跨70 m以上随桥面板的增厚而降低。对于常规结合桥面板，跨径越大则组合梁截面等效抗弯惯性矩也越大，预应力偏心弯矩在组合截面顶部产生的预压应力越小，因此常规结合桥面板上表面获得的预压应力水平显著降低，更多的预压应力为钢主梁所承担。分析结果表明，后结合预应力法在主跨50 m以上的连续组合梁中具有较高的应用价值，相较于常规预应力法，在相同配束条件下，后结合桥面板能始终获得较高的预压应力储备，且不会在钢主梁中引入多余的压应力使得钢梁底板和腹板受压屈曲。然而后结合桥面板需要预留群钉孔，施工过程较常规预应力法更加复杂，因此在主跨40 m以下的连续组合梁中，常规预应力法仍具有较高的竞争优势。

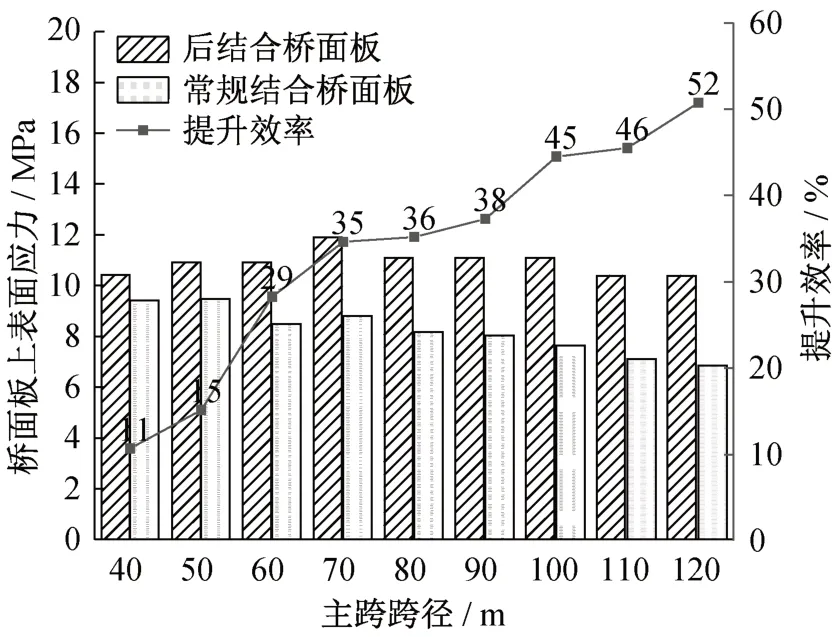
图12 后结合和常规结合桥面板上表面应力计算结果Fig.12 Calculation result of up surface stress in the post-combined deck and the conventional precombined deck

4 后结合预应力法的应用方案

针对组合梁负弯矩区顶板混凝土受力的不利情况，目前工程上采用了三种设计准则［14］设计混凝土桥面板：①混凝土始终处于受压状态的全预应力构件，②混凝土允许受拉但不允许开裂的A类构件，③混凝土受拉允许开裂，但严格控制裂缝宽度的B类构件。

为了得到不同跨径后结合预应力组合梁的合理钢束布置方案，在第3节的研究基础上，计算频域组合和准永久组合作用下中支点桥面板上表面的拉应力。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）［16］给出了全预应力构件和部分预应力的A类构件需要满足的条件，表3列出了不同设计准则下，后结合和常规结合桥面板分别所需的钢束数量。以预应力钢束最低布置为限制条件，对于宽度为6 800 mm的桥面板，预制后结合桥面板最多可以布置125根钢束，现浇桥面板最多可以布置115根钢束。从表中可以看出，后结合预应力组合梁在负弯矩区桥面板内配置较少的预应力钢束就能达到常规预应力组合梁相同的效果。常规结合桥面板在主跨40 m以上无法满足全预应力构件要求，在主跨70 m以上无法满足部分预应力A类要求。后结合桥面板在主跨70 m以下都能满足全预应力构件要求，在主跨110 m以下都能满足部分预应力A类要求，说明后结合预应力法可以提高预应力使用效率，进一步改善桥面板的抗裂性能。

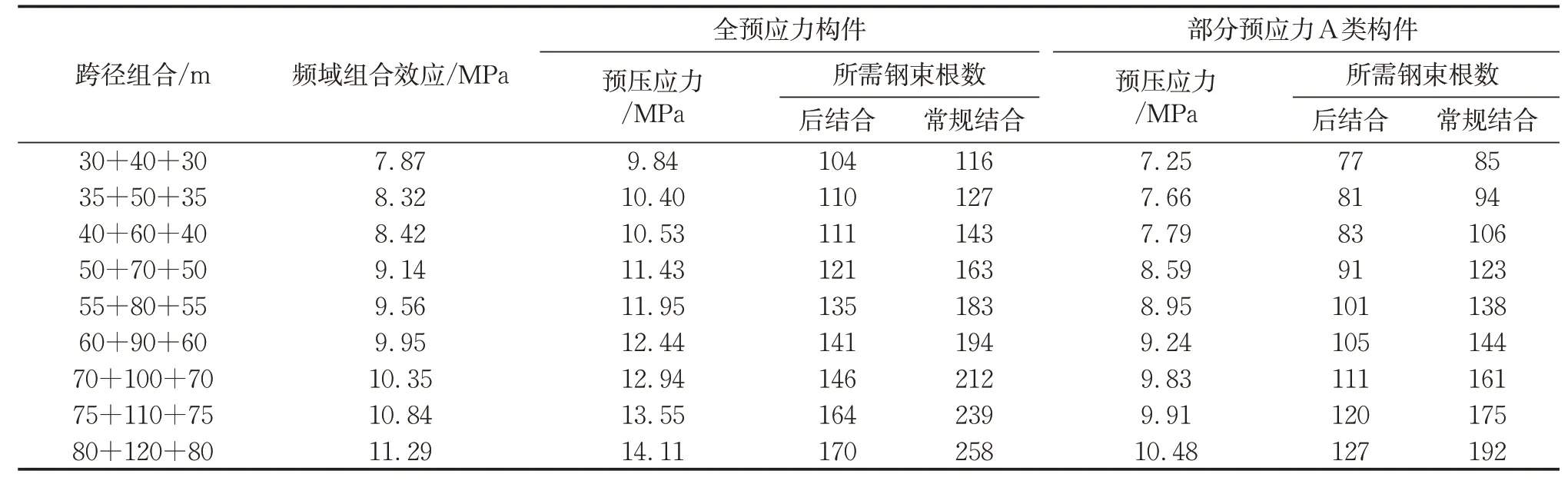
表3 不同设计准则下桥面板所需钢束数量Tab.3 Required number of prestress strands for the bridge deck under different design principles

5 结语

本文通过对首次采用后结合预应力法的一大跨度连续组合梁桥进行实桥测试，结合理论和有限元分析，进一步研究了后结合预应力技术在钢混组合梁桥中合理的适用范围，得出如下结论：

（1）现场测试结果表明，对于采用钢套箱群钉连接件的后结合预应力组合梁，在张拉预应力前，负弯矩区钢主梁和混凝土桥面板可以完全分离，预应力仅施加于混凝土桥面板内，不会在钢梁上产生压应力，后结合预应力组合梁提高了预应力张拉效率，进而提高了负弯矩区桥面板的预应力储备。

（2）背景工程中，后结合法产生的预压应力效果比常规预应力法提高了30%。分析表明：在主跨50 m以上的连续组合梁中选择后结合法具有明显的优势，但是在主跨40 m以下选择常规预应力法仍具有较高的性价比。

（3）后结合预应力组合梁在主跨50～70 m中可以实现全预应力配束方案，在80～110 m中可以将桥面板设计成部分预应力A类构件，在120 m以上只能将桥面板设计成部分预应力B类构件。

作者贡献说明：

苏庆田：构思论文框架，指导试验设计、数据分析、论文写作与修改。

邹迪升：参与试验设计、完成数据分析及论文初稿的写作与修改。

张龙伟：参与实桥设计与数值分析，论文写作与修改。

陶仙玲：参与实桥测试。

黄超：参与实桥测试。