抗剪连接程度对组合梁受力性能影响

黄 侨，郑 兴，李文贤

（1.东南大学交通学院，南京 211189；2.江苏省交通工程建设局，南京 210004）

钢-混凝土组合梁是桥梁工程中常用的一种主梁形式，它合理地利用钢材和混凝土不同的受力特性，兼具有钢结构和混凝土结构的优点。在设计钢-混凝土组合梁时，为防止钢梁与混凝土翼缘板间出现过大的界面滑移，在混凝土翼缘板和钢梁之间需布置连接件，确保两者共同受力。根据连接件布置数量的多少，组合梁可以分为部分连接组合梁和完全连接组合梁。文献［1］中按照式（1）对抗剪连接程度η进行定量计算。

式中：n为连接件的数量；As和Ac分别为断面上钢梁和混凝土的面积；fd和fcd分别为钢和混凝土的设计强度；Ncv为单个连接件的抗剪承载力。在此，连接程度η可定义为在一个剪跨范围内实际的连接件数量与抗弯极限状态下所需的连接件数量之比。

自从Newmark［2］最早提出了考虑部分抗剪连接的组合梁的弹性分析理论之后，许多国内外学者都对抗剪连接程度对组合梁产生的影响开展了理论和试验研究。Ranzi和Zona［3］对部分连接组合梁进行研究时，推导了将混凝土板视为欧拉梁，钢梁视为铁木辛柯梁，再将二者耦合在一起的计算方法。荣学亮［4］进行了钢-混组合梁中的焊钉连接件的锈蚀疲劳试验研究。汪炳［5］开展试验，对焊钉连接件和开孔钢板连接件的滑移量进行了对比分析。Wang等［6］对不同连接程度的组合梁进行疲劳试验，对组合梁的疲劳寿命进行分析和预测。黄侨等［7］进行理论推导，得到了考虑界面滑移和剪切变形时组合梁下挠和截面应力的解析解，并通过试验验证了结果的正确性。

近年来，随着数值模拟方法的发展，有限元计算成为了除理论推导和实验研究外，分析复杂结构受力状态的重要方法之一。Queiroz等［8］采用ANSYS有限元软件，对完全连接组合梁和部分连接组合梁的荷载-滑移曲线、纵向界面滑移、焊钉剪力分布和破坏形态等进行了研究。Xing等［9］建立了钢-橡胶填充混凝土部分连接组合梁的有限元模型并进行参数分析。Classen等［10］采用有限元方法对钢-高强混凝土组合梁滑移不超过限值时的最小抗剪连接程度进行计算，随后针对T型钢梁的部分连接组合梁，研究了设计该类组合梁时应满足的要求［11］。Ozturk等［12］基于OpenSees软件平台建立了槽钢-混凝土部分组合梁的非线性纤维有限元模型。Zheng等［13］对有限元模拟组合梁受力状况时采用的建模方法和细节进行了讨论。

有限元计算的广泛应用有效节约了以往进行试验所需要耗费的成本和时间。采用有限元模型的数值模拟方法可以更加方便地对组合梁承载力和界面滑移等重要指标进行参数分析。然而，若将精细化模型计算至结构破坏，进行多因素、多水平的参数分析时，计算规模将会过于庞大。为此，可以采用正交设计，达到以部分试验代替全面试验的效果，随后对部分试验的结果进行数据分析，即可了解全面试验的情况［14］。

另外，研究钢-混组合梁抗剪连接程度对结构承载力和界面滑移的影响时，在参考现有计算公式形式的基础上［15］，可以将试验数据和有限元模型的计算结果进行公式拟合，从而得到能够更加有效和准确地预测组合梁承载力和界面滑移的计算方法，为组合梁设计提供参考。

为对不同抗剪连接程度的组合梁的受力状况进行研究，本文首先建立了4个布置不同数量焊钉的组合梁有限元模型，并进行梁式试验，通过将两者的结果进行对比，检验了有限元模型的正确性。随后基于ABAQUS软件的二次开发，实现了参数化建模，并针对焊钉数量、直径、长度和材料强度等因素，进行了正交设计和参数分析。最后，对抗剪连接程度对组合梁受力的影响展开讨论，拟合得到了不同抗剪连接程度的组合梁承载力和梁端滑移的计算公式。

1 建立有限元模型

1.1 几何模型

运用大型通用有限元软件ABAQUS，建立4个不同焊钉间距的钢-混凝土简支组合梁的有限元模型，分别编号为SCB-1至SBC-4。简支梁计算跨径为3.0 m，在建模时考虑到模型受力的对称性，为减小计算耗时，仅建立二分之一模型，并相应在跨中处设置对称边界约束。工字形钢梁的上翼缘板宽度为120 mm，下翼缘板宽度为160 mm，腹板高度为150 mm。翼板和腹板厚度均为10 mm。混凝土翼缘板断面尺寸为宽300 mm、高80 mm。按照构造要求，在混凝土板中共设置6根Φ6纵向钢筋和间距200mm的Φ6箍筋。组合梁的立面构造图及横断面图如图1所示。

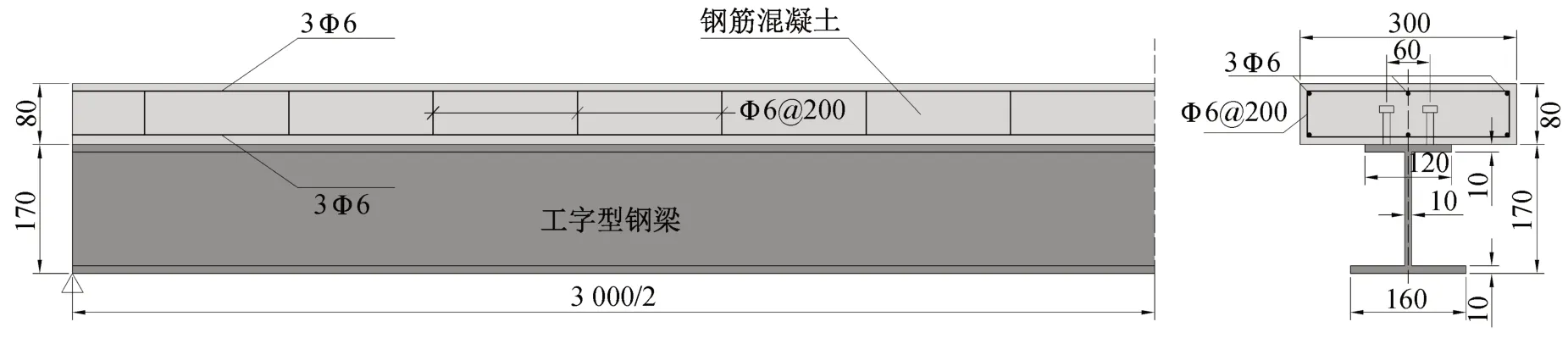
图1 组合梁构造图（单位：mm）Fig.1 General layout of composite beams(unit:mm)

抗剪连接程度η是本文中主要研究的对比参数。模型中采用双排布置的Φ13×60焊钉，横向间距为60 mm。模型SCB-1为完全抗剪连接（η=1），SCB-2和SCB-3设计为部分抗剪连接（η＜1），SCB-4则布置数量多于SCB-1的焊钉（η＞1）。4个模型的焊钉布置情况见表1。

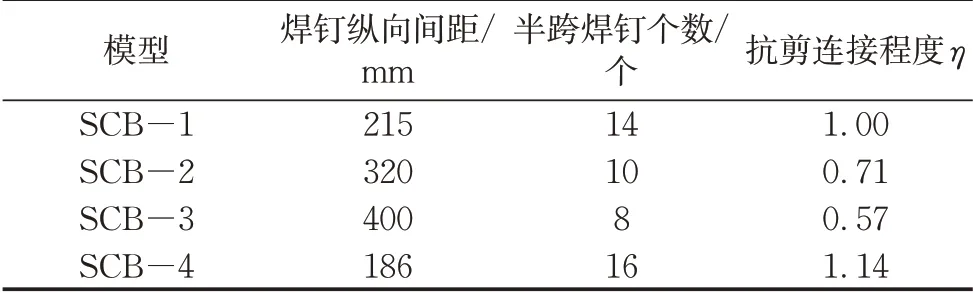
表1 焊钉布置情况表Tab.1 Distribution of studs

1.2 建模方法

为较准确地模拟混凝土板、工字钢梁和焊钉之间的接触，因此混凝土板、钢梁和焊钉均采用C3D8R实体单元，纵向钢筋和箍筋采用T 3D2桁架单元。为了更好地模拟焊钉及周边混凝土的受力状态，在焊钉附近对网格尺寸进行局部加密。划分网格后的有限元模型（以SCB-4为例）如图2所示。

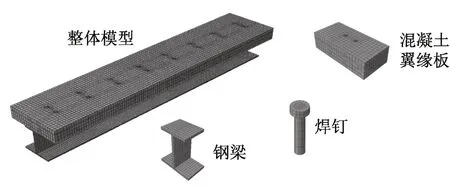
图2 有限元模型图Fig.2 Finite element model

根据材料试验结果［16］，得知混凝土抗压强度为38.5 MPa，并由此确定混凝土应力-应变曲线，在ABAQUS中定义了相应的混凝土本构模型。钢梁弹性模量为2.06×105MPa，屈服强度为352 MPa，钢筋弹性模量为2.0×105MPa，屈服强度为365 MPa，应力-应变曲线用双折线模型模拟。通过焊钉推出试验，得到焊钉的弹性模量为2.0×105MPa，极限强度为525 MPa。

在各个构件之间的接触设置上，ABAQUS提供了多种接触关系，结合模型试算和试验研究［13］，模型中主要采用的接触设置如表2所示。

表2 模型接触关系Tab.2 Contact relationship in models

在模型的支座位置，按照简支梁边界条件进行约束，跨中位置施加对称边界约束。加载时，在简支梁跨中的上方设置一个参考点，并对其施加竖直向下的位移。通过将参考点与混凝土顶面的一块区域进行耦合，使参考点的位移刚性地传递至混凝土顶面。

2 有限元模型的试验验证

2.1 试验布置

为验证ABAQUS有限元模型的有效性和正确性，对试件SCB-1至SCB-4均进行了跨中加载的梁式试验。加载前期以10 kN·min-1的速率进行荷载控制，当加载至弹性极限荷载后，改为0.5 mm·min-1的位移控制加载直至破坏，得到其抗弯承载力。加载时对梁端的混凝土板底面和钢梁顶面的纵向位移分别进行观测，可得到梁端的荷载-滑移曲线。试验装置如图3所示。

图3 梁式试验装置图Fig.3 Setup of beam test

2.2 模型有效性验证

将有限元模型对试件SCB-1至SCB-4的计算抗弯承载力与其试验结果进行对比，如表3所示。结果表明，布置焊钉的数量对组合梁的抗弯承载力有明显的影响，即截面抗弯承载力随着连接程度的增加而略有提高。4个模型的有限元计算值和试验结果较为接近，其误差均不超过3%，同时也验证了有限元模型的有效性和正确性。

表3 跨中截面抗弯承载力计算结果及对比Tab.3 Results of bending capacity

将有限元计算结果与梁式试验得到的荷载-滑移曲线的全过程进行对比，如图4所示。图中可以看出，相对于抗弯承载力而言，抗剪连接程度对荷载-滑移曲线具有更为显著的影响，即滑移曲线随着连接程度的增加而明显延长。有限元模型和试验得到的荷载-滑移曲线趋势相同，结果基本吻合，说明本文有限元模型能够较为准确地模拟不同连接程度组合梁的界面滑移全过程。试验结果和模拟计算表明，当连接程度η=0.57～1.14时，承载能力极限状态下的界面滑移范围远超过1 mm，此时的滑移量较大恰恰是截面塑性抗弯承载力计算的必要条件。

图4 荷载-滑移曲线Fig.4 Curves of load-slip

3 参数分析

3.1 参数设置

为研究不同的焊钉数量（半跨）、长度、直径和材料强度对组合梁受力状态的影响，本文进行了主要影响因素的参数分析。相较于ABAQUS/CAE进行建模的方法，基于Python语言，利用ABAQUS脚本接口进行二次开发能够更加方便地实现参数化建模及分析。本文针对上述参数编写了Python脚本程序，实现参数化建模。分析中考虑的各因素及水平如表4所示。半跨的焊钉个数设置了6个水平，其余参数均设置3个水平。

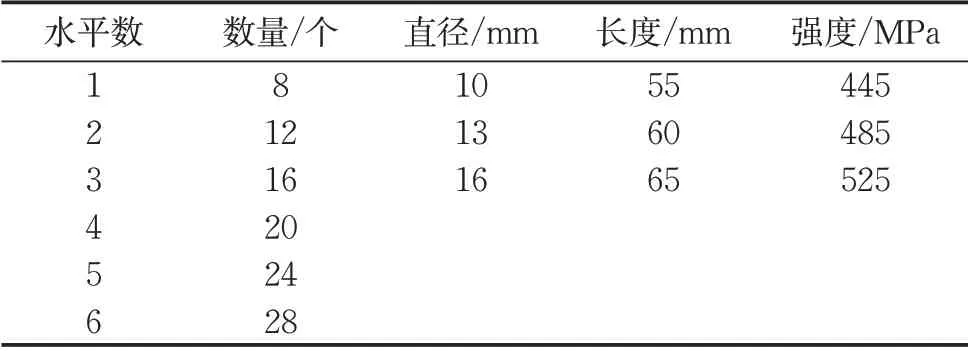
表4 各因素水平表Tab.4 Levels of different factors

若将所有参数水平组合全部进行计算所需要的计算代价太大，因此可采用正交设计，将各个因素的各个水平的组合进行合理的分配，实现因素和水平的整齐可比性和均匀分散性，从而达到用部分模型代替全面模型来了解各参数对结果影响情况的目的［14］。表5中给出了基于正交设计制定的混合水平正交表，并针对18个参数化模型分别进行有限元计算。例如表5中试验序号为1号的模型，其焊钉数量为8个（半跨内）、焊钉直径为10 mm、焊钉长度为55 mm、焊钉材料的极限强度为445 MPa。

表5 正交设计计算方案表Tab.5 Calculation scheme of orthogonal design

3.2 计算结果和数据分析

针对正常使用极限状态，《公路钢混组合桥梁设计与施工规范》（JTG/T D64-01—2015）［17］中要求结合面最大滑移小于等于0.2 mm。对于桥梁结构，正常使用极限状态下对应的荷载效应约为承载能力极限状态的0.55至0.65倍。因此，对正交设计有限元模型的0.6倍承载力下梁端滑移量进行数值模拟研究。对18个正交设计参数化有限元模型的计算结果如表6所示。

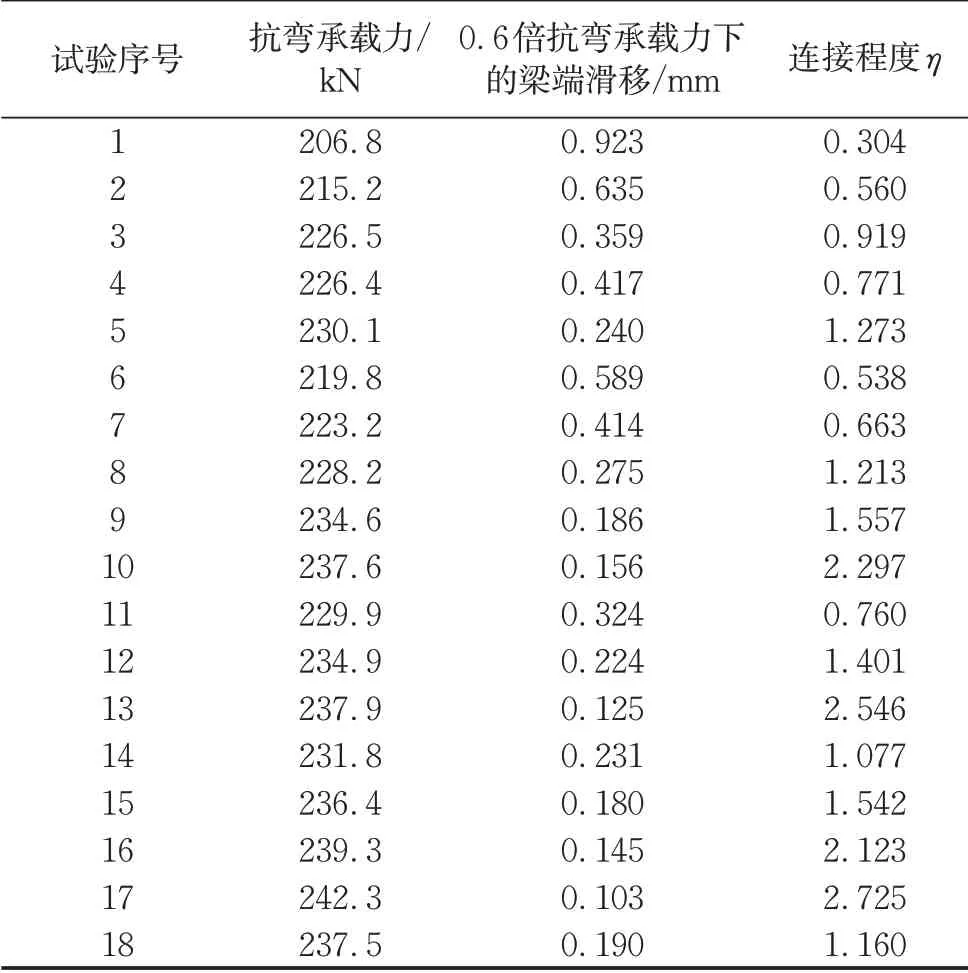
表6 基于正交设计的有限元模型抗弯承载力计算结果Tab.6 Results of finite element models in orthogonal test

在对抗弯承载力计算结果进行数据分析时，首先计算各因素下承载力的极差，判断各因素的总体影响程度。随后在方差分析中，对各列因素偏差平方和进行计算，并与误差偏差平方和进行对比，构造F统计量进行F检验，检验各个因素影响程度的显著性［14］，计算结果如表7所示。

表7中，Kij为第j列因素在i水平时对应的试验指标之和，kij为第j列因素在i水平时对应的试验指标平均值。分析表明，焊钉数量和直径对于钢-混组合梁抗弯承载力的影响最大，而焊钉长度和材料强度在考虑范围内影响甚微。这是由于在本文研究的范围内，焊钉数量和焊钉直径对组合梁的连接程度具有最直接的影响。更多的焊钉数量和更大的焊钉直径能够使组合梁具有更高的连接程度，加强钢梁与混凝土翼缘板之间受力的整体性，防止混凝土翼板的掀起和焊钉的断裂，从而使得组合梁具有更高的承载力。

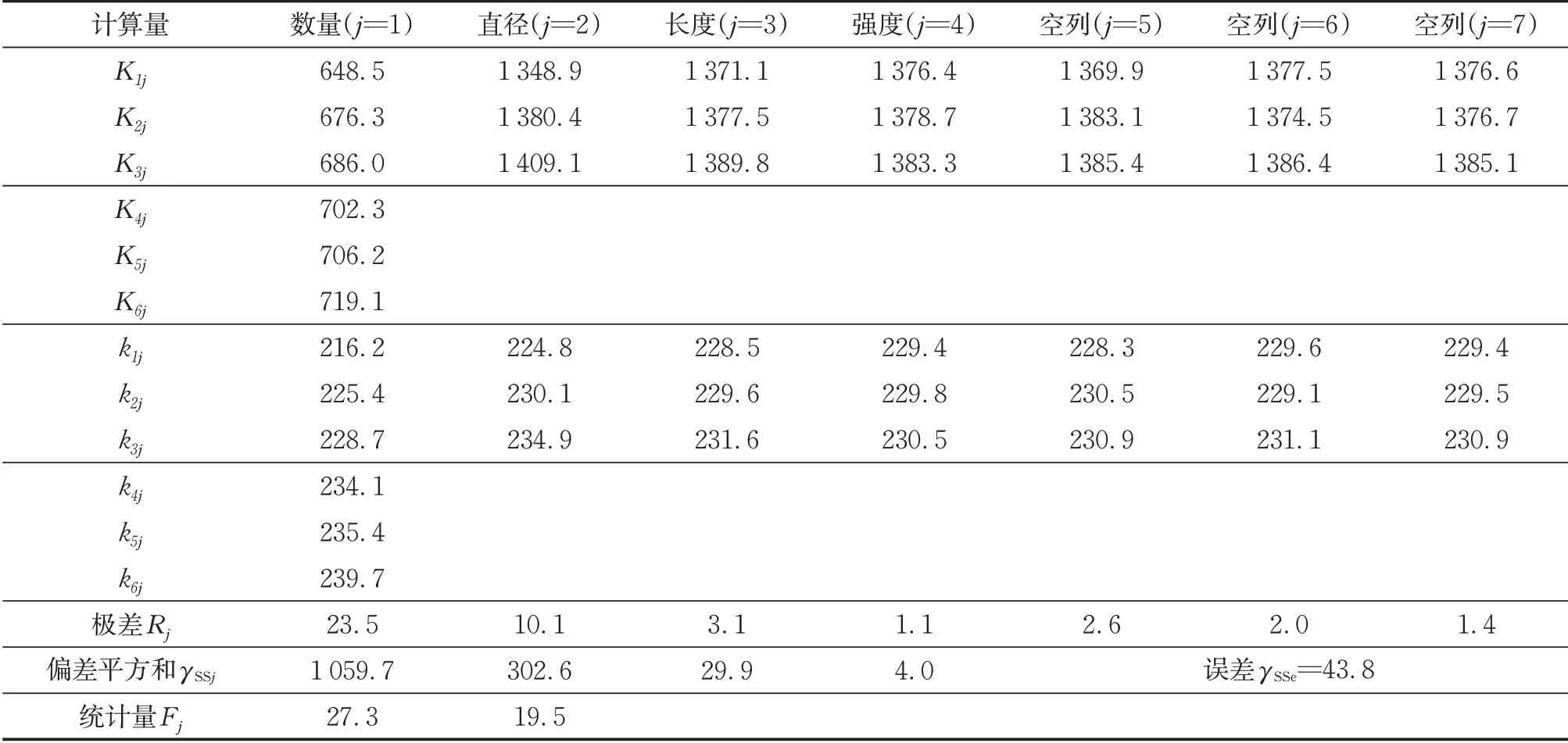
表7 抗弯承载力数据分析表Tab.7 Data analysis of bending capacity

在F检验时，仅对焊钉数量和直径的影响程度显著性进行检验。经检验，焊钉数量和直径的影响均在α=0.005水平显著，焊钉数量的影响尤为明显。各因素对组合梁承载力的影响如图5所示。

图5 各因素对抗弯承载力影响Fig.5 Influence of factors on bending capacity

按照同样方法对各个模型中0.6倍抗弯承载力时的梁端滑移计算值进行分析，结果如表8所示。

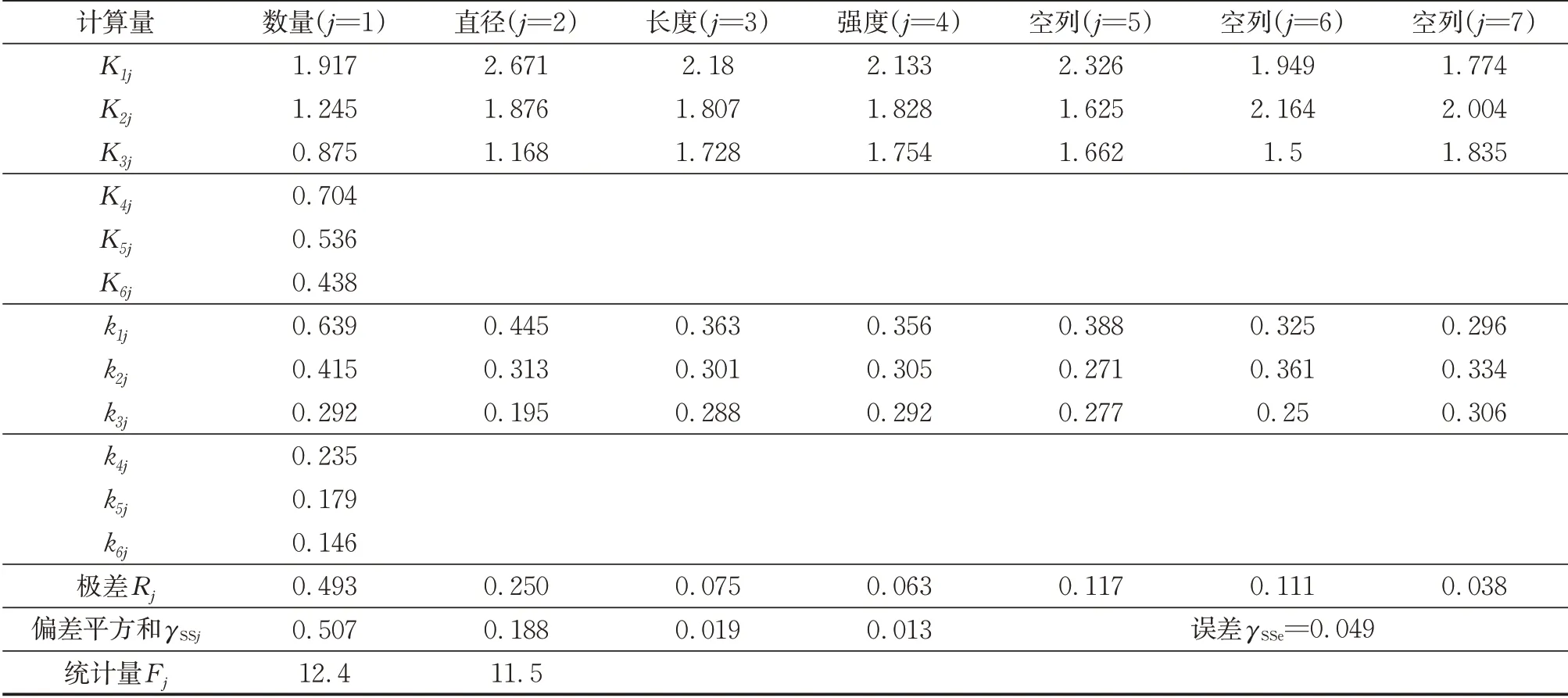
表8 梁端滑移数据分析表Tab.8 Data analysis of beam end slip

图6 为各因素对承载力的影响。图中可见各因素与组合梁梁端滑移均呈负相关。结合图6和表8可以发现，4个因素中，焊钉数量的影响最大，焊钉直径次之，而焊钉的长度与材料强度对正常使用极限状态下的组合梁滑移影响较小。焊钉数量对滑移的影响呈现出非线性，焊钉数量较少时，其对梁端滑移的影响相对更加明显。

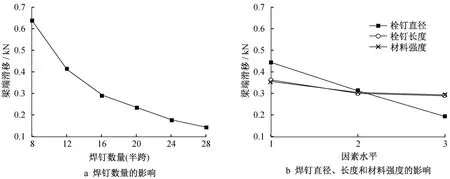
图6 各因素对梁端滑移影响Fig.6 Influence of factors on beam end slip

4 抗剪连接程度的影响分析

4.1 对承载力的影响

根据有限元计算的结果，可以通过公式拟合得到抗剪连接程度对钢-混组合梁抗弯承载力的影响。

对抗剪连接程度η不小于1.0的完全组合梁，一般认为其连接程度对承载力的影响不大。文献［18］认为完全连接组合梁的承载力与塑性抗弯承载力公式的计算结果较为吻合。完全连接组合梁的延性较高，在极限状态下，钢梁的下翼缘和部分腹板已进入强化阶段，界面滑移效应对抗弯承载力的影响较小。《钢-混凝土组合桥梁设计规范》（GB 50917—2013）［19］中，按照塑性设计方法，计算正弯矩作用下组合梁的抗弯承载力M的公式如式（2）～（3）所示。

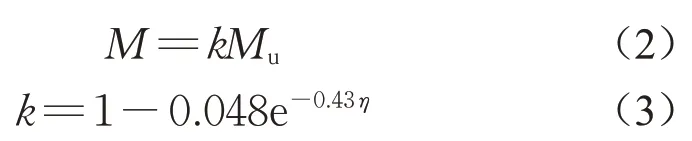
式中：k为考虑滑移效应的拟合系数；Mu为按照混凝土板与钢梁刚接计算的组合梁塑性承载力，即不考虑界面滑移的计算结果。当η=1.0时，k=0.96，即认为完全抗剪连接时，滑移效应对组合梁承载力的影响不大。

而部分连接组合梁的承载力通常由钢梁承载力Ms和完全连接组合梁承载力Mu内插得到，文献［15］和文献［20］分别采用式（4）的线性和式（5）的非线性内插进行计算。

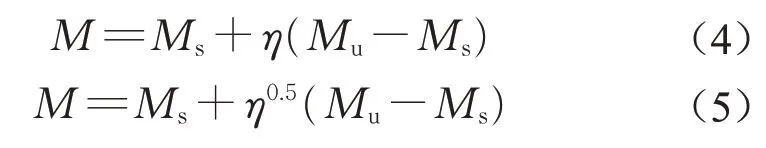
对正交设计的有限元模型计算中组合梁的连接程度与其抗弯承载力进行拟合，得到类似形式的拟合计算公式。对η≥1.0的完全连接组合梁，拟合公式如式（6），11个正交设计模型的拟合优度R2=0.60，精度可以接受。

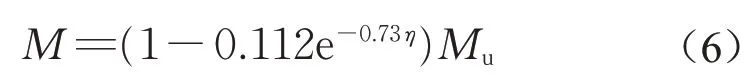
对η＜1.0的部分连接组合梁，拟合公式如式（7），7个正交设计模型的拟合优度R2=0.87，精度较高。

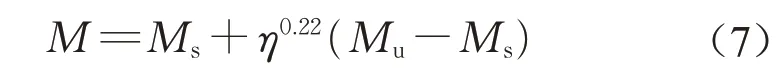
钢-混组合梁抗剪连接程度对抗弯承载力的影响及各公式的计算结果如图7所示。可以看出，采用线性内插式（4）计算部分连接组合梁的承载力将略偏于保守，本文拟合式（7）和非线性内插式（5）的曲线相对更符合有限元计算和梁式实验的结果。而对于完全连接组合梁，当1.0≤η＜1.5时，有限元的计算结果与式（2）和式（6）的计算结果吻合较好，误差均不超过5%，当连接程度大于1.5时，各计算公式和有限元模拟结果则几乎完全吻合。

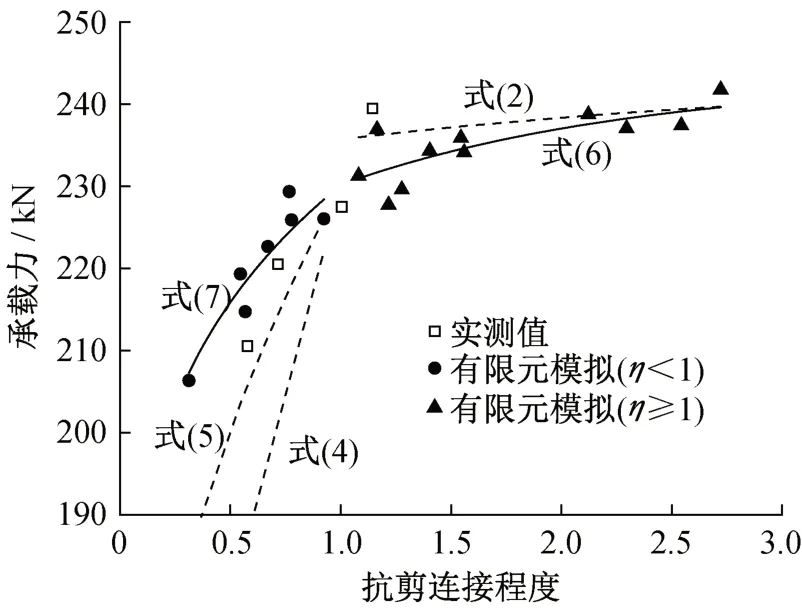
图7 抗剪连接程度对承载力的影响Fig.7 Influence of shear connection degree on bearing capacity

4.2 对梁端滑移的影响

图8 给出了18个正交设计模型在0.6倍抗弯承载力时梁端滑移值与梁式试验实测值的比较。两者的分布规律大致相同，随着抗剪连接程度的增加，梁端滑移将逐渐减少，并趋于稳定。对有限元模型计算得到的数值进行数据拟合（图8中的曲线），可以得到：

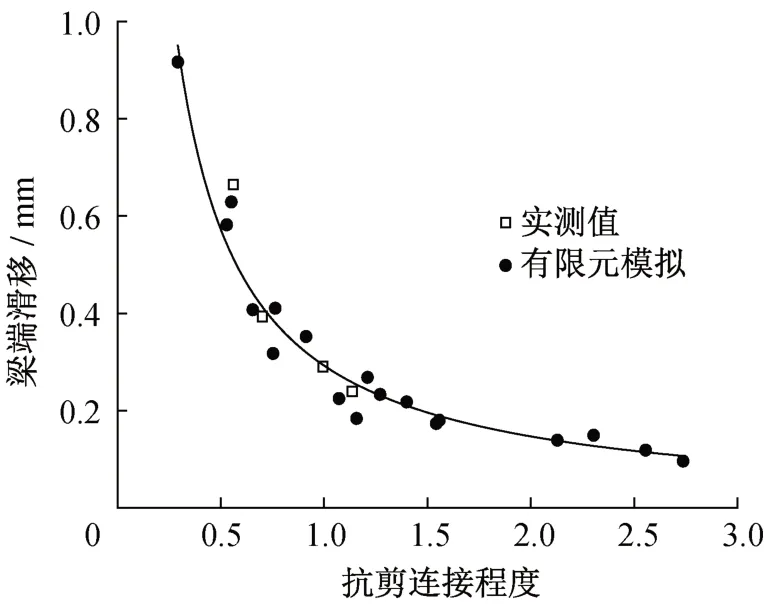
图8 抗剪连接程度对梁端滑移的影响Fig.8 Influence of shear connection degree on beam end slip

18个正交设计模型的拟合优度R2=0.96，拟合程度很好。此时将s=0.2 mm代入，可得η=1.5，即当抗剪连接程度大于1.5时，钢-混组合梁的梁端滑移量将小于0.2 mm。

抗剪连接程度是一个基于连接件布置的相对指标，而规范中焊钉抗剪承载力的设计值往往比实际值偏低，因此组合梁的连接程度往往偏安全地被低估。同时，在实际桥梁工程中，根据《公路钢混组合桥梁设计与施工规范》（JTG/T D64-01—2015）［17］的构造要求，出于抗疲劳、耐久性及密实混凝土的考虑，焊钉连接件的间距通常取100～300 mm，且横向可布置2～6列，此时连接件的布置已较为密集，钢-混组合梁抗剪连接程度一般远大于1.0。所以在正常使用极限状态下，规范［17］中针对连接件的“结合面最大滑移小于等于0.2 mm”的要求一般不控制设计。

5 结论

对不同抗剪连接程度的钢-混凝土组合梁进行有限元模拟和梁式试验，针对其承载力和界面滑移等问题展开研究，并进行基于正交设计的参数分析，进一步讨论了抗剪连接程度对组合梁受力的影响，可供钢-混凝土组合梁桥设计参考。本文研究得出的主要结论如下：

（1）通过将有限元模型计算结果与梁式实验结果进行对比，可以发现有限元模型不仅可以较为精确地对组合梁进行承载力计算，还可以模拟不同抗剪连接程度时组合梁界面滑移全过程的发展情况。

（2）利用正交设计和参数化有限元计算方法研究组合梁中配置的焊钉数量、长度、直径和材料强度等因素对组合梁抗弯承载力和梁端滑移的影响。结果表明，焊钉数量对组合梁的受力状态影响最大，其次是焊钉直径，而焊钉长度和焊钉材料强度在本文研究的范围内影响相对较小。

（3）在钢-混组合梁的承载力计算中，需对部分连接组合梁和完全连接组合梁分别讨论。部分连接组合梁的承载力应由钢梁承载力和完全刚性连接的组合梁承载力非线性内插得到，文中式（7）的拟合效果较好。连接程度η≥1.0时对组合梁的抗弯承载力影响很小，或可选用文中拟合式（6）或规范中采用的式（2）进行计算，均可得到较为准确的结果。

（4）若偏安全地采用组合梁承受0.6倍抗弯承载力时的梁端滑移量来考虑桥梁在正常使用极限状态下的滑移，式（8）可以较好地拟合组合梁抗剪连接程度与梁端滑移之间的关系。当抗剪连接程度η大于1.5时，0.6倍承载力下梁端滑移即可小于0.2 mm。

作者贡献说明：

黄侨：研究选题，提供研究思路和技术指导，论文审定。

郑兴：有限元计算，数据处理与论文撰写。

李文贤：有限元建模与正交设计。