纵向数据缺失和辅助信息下分位数回归模型的估计

张雨婷,罗双华,张成毅

(1.西安工程大学 理学院,陕西 西安 710048; 2.西安交通大学 经济与金融学院,陕西 西安 710049)

0 引 言

在抽样调查、人口普查、生物医学、计量经济学等研究领域，经常产生大量的纵向数据。然而，在纵向数据的研究中时常会遇到数据的缺失，因此处理完整观测数据的传统推断方法将不再适用。例如，随机区组、重复测量设计以及大型数据回归分析等都要求数据完整。对于这些缺失数据，如果剔除缺失的部分数据而仅用完全观测到的数据进行统计推断，那么所得到的估计往往产生偏差。因此，如何对纵向数据缺失进行有效的统计分析和推断，已成为该领域的研究热点，取得了众多的研究成果[1-4]。

变量随机缺失下的分位数回归模型在经济学、金融学、医学和生态学等领域应用广泛，目前已有大量研究[5-8]。OWEN提出的经验似然法是在完全样本下的一种非参数统计推断方法[9]。由于其具有自动确定置信域形状和方向的优点，许多学者在处理缺失数据的问题上应用了经验似然方法[10-14]。为了提高估计效率，WHANG和OTSU引入了光滑方法,研究分位数模型的经验似然估计[15-16]。这种光滑经验似然方法是很有意义的，迄今已有大量研究[17-20]。在上述研究基础上，通过加入辅助信息可以提高估计的有效性[21-24]。其中，TANG等首次在正态逼近的基础上应用逆概率加权方法，研究了含有辅助信息的线性分位数模型的经验似然估计[21]。但其方法在进行推理时须估计复杂的协方差矩阵。此外，WHANG认为标准的Bootstrap理论不能直接推理分位数回归模型的估计[15]。故在此基础上，LYU等提出了基于光滑经验似然方法研究辅助信息下分位数模型的参数估计问题，不仅包含了辅助信息，而且避免了估计复杂的协方差矩阵[22]。

综上所述，基于纵向数据缺失且具有辅助信息的线性分位数回归模型的统计推断还有很多问题值得讨论。因此，本文在纵向数据响应变量随机缺失的情形下，运用辅助信息下分位数回归模型的经验似然方法给出了参数估计，并在一定条件下证明了所得估计的大样本性质。

1 似然估计及主要结果

1.1 纵向数据缺失下的经验似然估计

考虑如下纵向数据线性分位数回归模型：

(1)

式中：Yij为第i个个体的第j次观测值；Xij为已知的p维设计点列向量；β是p维未知回归系数向量；εij是随机误差且满足P(εij<0|Xij)=τ，这里τ∈(0,1)是分位数水平。记εi=(εi1,εi2,…,εini)T，那么{εi,i=1,2,…,n}相互独立，但对同一个i(i=1,2,…,n)，εij1和εij2(j1≠j2)不独立。

在数据没有缺失时，模型(1)定义线性分位数回归估计为

(2)

式中：B为参数空间；ρτ(u)=u{τ-I(u<0)}是分位数损失函数。

当模型(1)中响应变量Yij缺失时，引入变量δij表示Yij可观测到的示性函数，即Yij可观测到时δij=1，否则δij=0。假设MAR缺失机制可表示为

P(δij=1|Yij,Xij)=P(δij=1|Xij)=π(Xij)

(3)

式中：π(Xij)=P(δij=1|Xij)为选择概率函数。由于在实际问题中，π(Xij)往往是未知的，因此，采用核估计方法进行估计，可以得到

式中：K(·)被称为核函数；hn为窗宽。则模型(1)在响应变量缺失下的加权分位数回归估计为

在以上的模型假设下，β满足如下估计方程：

(4)

式中：ψ(Y,X,β)=I(XTβ-Y)-τ是分位数得分函数，I(·)为示性函数。

定义Xi=(Xi1,Xi2,…,Xini)T为第i个个体的ni×p设计矩阵，

Xj=(X1j,X2j,…,Xnij)T,

Yi=(Yi1,Yi2,…,Yinj)T

ψi(β)=ψi(Yi,Xi,β)=

(ψ(Yi1,Xi1,β),ψ(Yi2,Xi2,β),…,

ψ(Yini,Xini,β))T

根据式(4)可定义,β的估计方程为

(5)

(6)

根据Lagrange乘子法计算可得β的对数经验似然比为

(7)

其中λ=σ(β)是方程

(8)

的解。进而可以得到β的经验似然估计

(9)

1.2 具有辅助信息的经验似然估计

在实际的统计推断中，关于协变量的辅助信息是可用的。通过

E(g(Ui,θ))=0

考虑模型的辅助信息,称g(Ui,θ)为模型的辅助信息量函数。其中，g(Ui,θ)∈Rr，θ为辅助信息量函数的参数，θ∈Rp且r≥p，Ui表示可以观测到的样本。g(Ui,θ)包含了可以从Ui的概率分布知识中推导出来的一大类信息，从而可以提高估计的有效性。

为了使用辅助信息，定义如下经验似然函数:

(10)

用Lagrange乘子法，求出权重ωi的估计：

(11)

其中γ是方程

(12)

的解。

(13)

(14)

(15)

1.3主要结果

设s是大于或等于2的整数，定义g(Xij)为Xij的密度函数，F(u1,u2,…,um|x)为εi=(εi1,εi2,…,εim)T的联合分布函数，Fj(uj|x)为当Xi=x时εij的边缘分布函数。在Legbesgue测度下，设f(u1,u2,…,um|x)为εi的联合概率密度，fj(uj|x)为εij的边缘密度。 令

f(u|x)=diag[f1(u1|x),f2(u2|X),…,

fm(um|x)]

在证明本文的主要结果之前，给出所需要的一些正则化条件：

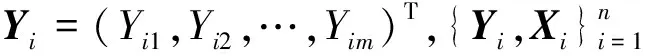
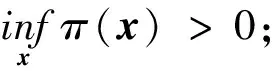
A3：K(·)是一个s(s>1)阶核函数，它有界且有紧支撑[-1,1]，且存在正常数C1,C2和ρ，满足C1I{|u|≤ρ}≤K(u)≤C2I{|u|≤ρ};

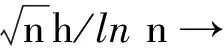
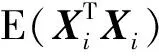
A6：函数g(Ui,θ)是有界的，矩阵S,B正定。

定理1 假设条件A1～A6成立，则有

定理2 假设条件A1～A6成立，则有

其中，χ2(p)表示自由度为p的卡方分布。

2 定理的证明

2.1引理

首先给出一些引理，再给出定理1、2的证明。

引理1 假设条件A1～A5成立，则有

证明类似于文献[6]中的引理6.7，从略。

引理2 设

rn=(lnn/(nh))1/2+hs，gn(x)=

在条件A2、A3成立下，若lnn/(nh)→0，则有

证明类似于文献[6]中的引理6.1，从略。

引理3 设条件A5～A6成立，则有

其中θ=E(g2(Ui,θ))。

证明类似于文献[6]中的引理6.4，从略。

引理4 设条件A6成立，则有

‖γ‖=Op(n-1/2)

证明类似于文献[6]中的引理6.5，从略。

引理5 假设条件A1～A6成立，则有

证明由引理4，可得γTg(Ui,θ)=op(1)，根据式(11)和(12)以及引理3易得nωi=1-γTg(Ui,θ)(1+op(1))，则有

(16)

由引理2以及Taylor展开式,易得

(17)

根据条件A4，A5以及式(17)得

由条件A6和式(16)以及引理4得

(π(Xij))-1ψi(β0)=

由γTg(Ui,θ)=op(1)，使用相同的计算过程得

根据条件A6和式(16)以及引理4，使用相同的计算过程可得，

因此，

其中，

根据中心极限定理以及大数定律，引理5得证。

2.2 定理1的证明

将式(14)进行Taylor展开,得

由引理5可得，

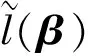
类似可推导出，

由中心极限定理可得

与文献[16]中式(28)～(30)证明类似，有

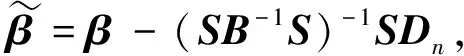
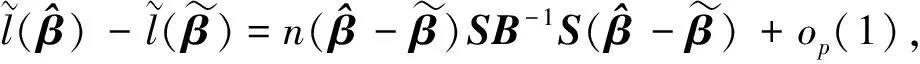
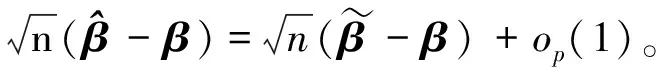
定理1得证。

2.3定理2的证明

即

(18)

由引理1可得，

则式(18)可变形为

即

(19)

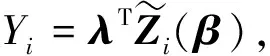
记

则有

因此式(19)第3项的上界为

即式(19)可改写成，

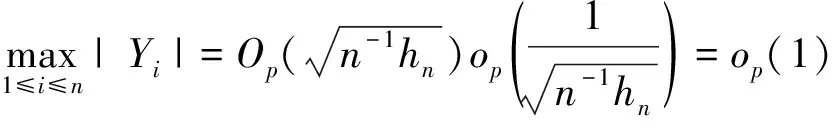
A-1(β)B2(β)+op(1)

其中，

根据引理1和引理5，定理2得证。

3 数值模拟

通过数值模拟实验验证所提出方法的有限样本性。考虑模型(1)

式中：协变量X的观测值Xij来源于N(0,1)分布，εij来自于正态分布N(0,1)，取β=1p。在模拟研究中，取τ=0.5,0.8，且对于不同的样本量n=100,200,300，基于3种选择概率函数分别产生2 000个随机样本：

π3(x)=0.6,x∈R

以上3种选择概率函数对应的平均缺失率分别约为0.07、0.26和0.40。选取核函数

表1 置信水平为0.95的置信区间的覆盖概率

表2 置信水平为0.95的置信区间的平均区间长度

由表1～2可以看出：

1) 对于选择概率π1(x)，WAQEL方法比NAQEL方法、CAQEL方法和NA方法得到更高的覆盖概率，但有更长的置信区间；对于选择概率π2(x)和π3(x)，WAQEL方法比NAQEL方法、CAQEL方法和NA方法都好，因为它得到更短的置信区间和更高的覆盖概率。表明当缺失概率比较大时，分位数加权十分必要。对3种选择概率，WAQEL方法得到的覆盖概率和区间长度和NAQEL方法得到的几乎接近，说明加权分位数且具有辅助信息的经验似然方法的效果较好。

3) 对于每一种缺失率，随着n增加，置信区间长度减小并且收敛概率增加。显然，当样本个数不变时，缺失率也影响置信区间长度和收敛概率。一般而言，当缺失率增加时，区间长度增加且覆盖概率减小。

可见，对于模型(1)，WAQEL方法表现出较好的结果。

4 结 语

本文应用逆概率加权方法和辅助信息下的经验似然方法相结合，给出了纵向数据响应变量随机缺失下线性分位数回归模型参数估计。在一定正则条件下，证明了所得估计量的渐近正态性。同时，用辅助信息下加权的经验似然方法减小了参数估计的方差，提高了估计效率。