考虑三源不确定性的Wiener过程航空发动机剩余使用寿命预测
赵广社,赵春涛
(1.西安工程大学 电子信息学院,陕西 西安 710048;2.西安交通大学 电子与信息学部,陕西 西安 710049)
0 引 言
航空发动机作为飞机的核心部件,其可靠性和安全性至关重要。但是,航空发动机不仅结构复杂,而且运行环境复杂多变,因而航空发动机的故障具有易发生、模式多、多故障模式同时存在等特点。预测与健康管理(prognostics and health management, PHM)是一种降低故障率、保证飞行安全的有效方法[1],其中RUL预测是PHM中的关键技术之一。RUL可以定义为系统或部件可继续正常使用的时间长度[2],即当前时刻与失效时刻之间的时间间隔。RUL预测通过分析监测数据或建立合适的性能退化模型对系统或部件的RUL进行预测。
现有RUL预测方法分为3类:基于经验的预测方法[3]、数据驱动的预测方法[4]和基于物理失效模型的预测方法[5]。基于经验的预测方法易理解、易实现[6],但其预测精度有限,并且依赖大量历史数据。基于物理失效模型的预测方法具有预测精度高的优点[7],但需要构建准确的物理失效模型,对航空发动机这种复杂系统来说极难实现。基于数据驱动的预测方法通过挖掘退化数据内在的信息[8],以表现系统自身变化及工作环境影响导致的系统失效,它避免了复杂的物理失效模型的构建过程,且准确率较高。因此,本文主要研究的是基于数据驱动的航空发动机RUL预测。
目前,基于数据驱动的RUL预测是研究的热门,并且拥有大量成熟的退化模型,如随机系数模型[9]、随机过程模型[10]和滤波模型[11]等。在基于随机过程的退化模型中,常常采用Wiener过程退化模型。WANG提出了基于EM算法的退化模型未知参数估计方法[12]。刘君强等通过实验证明了航空发动机的退化过程可以划分为几个不同的退化阶段[13]。黄亮等建立了多阶段Wiener过程性能退化模型,并实现航空发动机的RUL预测[14]。然而,对于发动机这种复杂系统,在退化过程中还普遍存在三源不确定性,即时变不确定性[15]、个体差异不确定性[16]、测量不确定性[17]。现有关于三源不确定性的文献较少。ZHENG等首次将三源不确定性引入到线性Wiener过程退化模型中[18],然而,该文献并没有考虑退化过程中的非线性性,WANG等同时考虑了非线性性和三源不确定性,并且证明了考虑三源不确定性可以有效提高预测精度[19]。DONG等利用粒子滤波实现了对锂电池的RUL预测[20]。王玺等同时考虑三源不确定性和非线性实现对航空发动机排气温度裕度的预测[21]。然而,上述考虑三源不确定性的研究中,在考虑测量不确定性时都假设测量误差服从正态分布,但正态分布不适合用来描述极端值(测量误差较大)出现概率较大的情况。
对于目前航空发动机RUL预测存在的问题,本文建立了考虑三源不确定性的非线性Wiener过程性能退化模型,将三源不确定性引入退化模型并且假设测量误差服从Logistic分布。提出一种基于最大熵无迹粒子滤波和条件期望最大化算法的参数估计方法。最后,采用大型涡轮风扇发动机数据集C-MAPSS进行仿真实验,验证本文方法的有效性。
1 三源不确定性的剩余寿命预测方法
1.1 模型描述
性能退化过程{X(t),t>0}被标准Brown运动B(t)驱动,那么一般的非线性Wiener过程可表示为
(1)
式中:λ为漂移系数;σB为扩散系数;ρ(τ,θ)为时间t的非线性函数;θ为未知参数;x0为初始退化状态,x0=0。如果ρ(τ,θ)=ρ那么该式就变成线性退化模型,可见该退化模型不失一般性。
从实际角度出发,个体差异不确定性是指同型号同批次的航空发动机,受到不同的外部工作环境和内部因素的影响,不同个体的性能退化过程也是存在差异的。因此,在退化模型中引入个体差异不确定性是必要的。根据文献[22],假设漂移系数λ为随机参数,来表现个体间差异的不确定性,建立参数λ的更新机制为
λn=λn-1+γ
(2)
受到传感器精度、外部运行环境噪声等因素的影响,测量误差是不可避免的。因此,有必要在建立退化模型时引入测量误差不确定性。为了表示这种测量误差,令测量过程{Y(t),t>0}为
Y(t)=X(t)+ε
(3)
式中:ε为测量误差。为了更好地拟合测量误差极端值出现概率较大情况下的退化过程,假设ε服从Logistic分布。
Logistic分布与正态分布形状相似,其概率密度函数为
(4)
式中:v为位置参数;s为尺度参数。由式(4)可以算出Logistic分布的超额峰度系数为1.2。通过超额峰度系数可知Logistic分布具有尖峰、厚尾的特征,因此Logistic分布比正态分布适合描述测量误差极端值出现概率较大的情况,Logistic分布也就常被用来在统计推断中增加推断的可靠性。同时,假设ε、λ和B(t)是相互独立的。
可以得出性能退化数据X(x1,x2,…,xn)的考虑三源不确定性的非线性Wiener过程性能退化模型的状态空间模型为
(5)
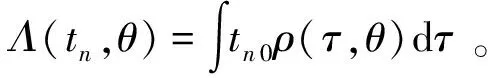
至此,已经在非线性退化模型中引入了三源不确定性。将性能退化状态xn和随机参数λn作为“隐含”状态,进一步整理式(5)可得退化模型的状态空间模型:
(6)
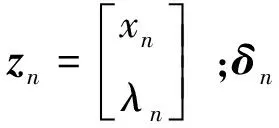
1.2 关键检测参数选取
实际上,每一个监测参数对退化过程造成的影响不同,为了进行准确的RUL预测,要筛选出对退化过程影响大的监测参数[23]。航空发动机的退化过程是必然发生且不可逆转的,对发动机退化过程贡献大的参数应具有单调性的特点。文献[24-25]采用定性分析监测参数的单调性来筛选关键参数,但该方法只是定性分析,并没有对参数的变化趋势进行量化,不能区分不同参数的变化程度。因此,采用Spearman系数计算各个监测参数的单调趋势,可表示为
(7)

由式(7)可以看出,Spearman系数的取值范围为[-1,1]。当参数值是常数或者随时间变化随机变化时,那么Spearman系数值为0;参数值随时间变化增加时,Spearman系数值大于0,参数值随时间变化的单调增加趋势越,Spearman系数值越接近于1,当参数值随时间完全单调增加时,Spearman系数值为1 ;参数值随时间变化的单调减少趋势越明显,Spearman系数值越接近于-1,当参数值随时间完全单调减少时,Spearman系数值为-1。
基于上述分析,为了使选取的监测参数拥有明显的单调性同时能够尽量全面地表现航空发动机的退化过程,选取趋势值超过阈值0.5的参数进行后续的航空发动机RUL预测。
1.3 最大熵无迹粒子滤波算法
用监测数据Y0:n估计的zn的期望和协方差分别为
(8)
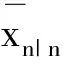
一步前向的期望和方差为
(9)
根据上述假设,可以用最大熵无迹粒子滤波算法联合估计性能退化正态和随机参数组成的zn。
根据式(6),基于监测数据Y0:n,RUL的概率密度函数可表示为
(10)
式中:
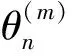
2 实例验证
2.1 数据来源
为验证所提方法的有效性,在C-MAPSS数据集上进行航空发动机RUL预测实验。该数据集是美国航空航天局预测中心提供的一组C-MAPSS工具模拟产生的由正常运行到失效的过程数据集。该数据集包含4组不同工作环境与不同故障模式下的数据集,包括引擎单元号、时间戳、3种配置以及 21 个传感器读取的数据,其中21个传感器数据和3个工作环境配置参数用来记录发动机的整个性能退化过程。每个数据集包括训练集、测试集和RUL预测子集。第1组训练集数据是在同一种运行环境下发生的单一故障的集合,包含100个发动机的监测样本,本文选取单一故障模式的第1组数据进行后续实验。
2.2 关键参数选取
根据1.2的分析,选择FD001中监测数据样本进行实验,计算Spearman系数得到如图1所示的参数变化趋势结果图。
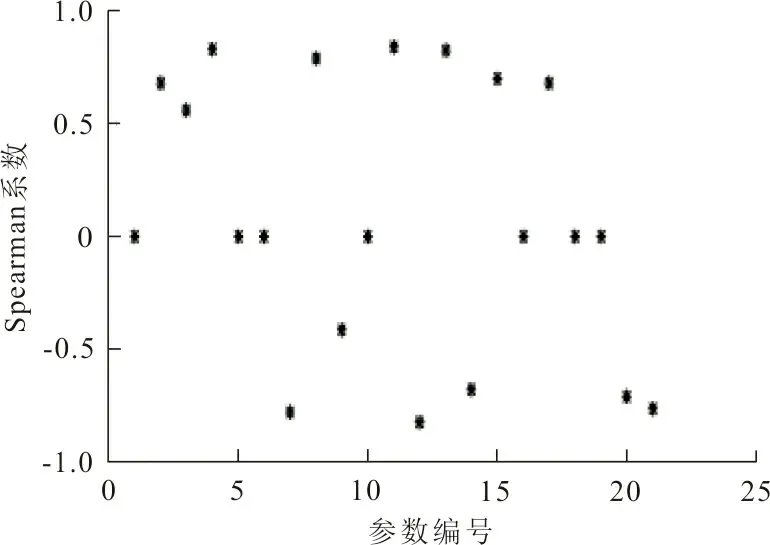
图 1 参数变化趋势Fig.1 Parameter variation trend
从图1可以看出,数据集里的21个传感器参数有常数(Spearman系数为0)、单调增加(Spearman系数为正)与单调减少(Spearman系数为负)3种情况。为便于后续计算,选取拥有单调递增趋势的参数,但本文方法不会受到监测数据单调趋势的影响。符合单调递增的参数序号为2、3、4、8、11、13、15、17,其趋势值如表1所示。
2.3 航空发动机RUL预测
由航空发动机的历史性能退化数据建立考虑三源不确定性的航空发动机性能退化模型。首先,利用Spearman系数对21个监测参数进行筛选。其次,在确定了关键参数的基础上,利用最大熵无迹粒子滤波和ECM算法,进行参数先验分布的估计。最后,在获得新的性能退化数据后通过模型参数的在线更新得到参数后验分布。RUL预测的具体步骤如图2 所示。

图 2 RUL预测流程图Fig.2 Flow chart of remaining useful life time prediction
为验证所提方法的有效性,选取M1方法进行对比实验[19],实验分为3个方面进行:首先,将本文方法与M1方法分别对航空发动机性能退化数据进行RUL预测,对比2种预测方法的预测精度;然后,使用M1中卡尔曼滤波与ECM算法相结合的模型参数估计方法估计模型的未知参数,分别采用本文模型与M1模型进行航空发动机RUL预测;最后,分别用最大熵无迹粒子滤波与ECM算法相结合的参数估计方法和M1中卡尔曼滤波与ECM算法相结合的参数估计方法对退化模型的未知参数进行估计,使用本文模型作为航发动机的退化模型进行航空发动机RUL预测对比实验。
M1方法:同时考虑三源不确定性和非线性性,但其假设测量误差服从正态分布,不能很好地反应测量出现极端值的情况。并且,在参数估计过程中,模型参数一旦确定,就不会再随退化数据的累积而更新。
为更好地衡量比较结果,本文选取RUL预测领域常用的MSE作为指标,该指标可以很好地表现RUL预测的精度和不确定性,计算公式为
(11)
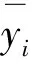
图3给出了2种预测方法在航空发动机从出厂到失效的所有观察点的MSE对比结果。
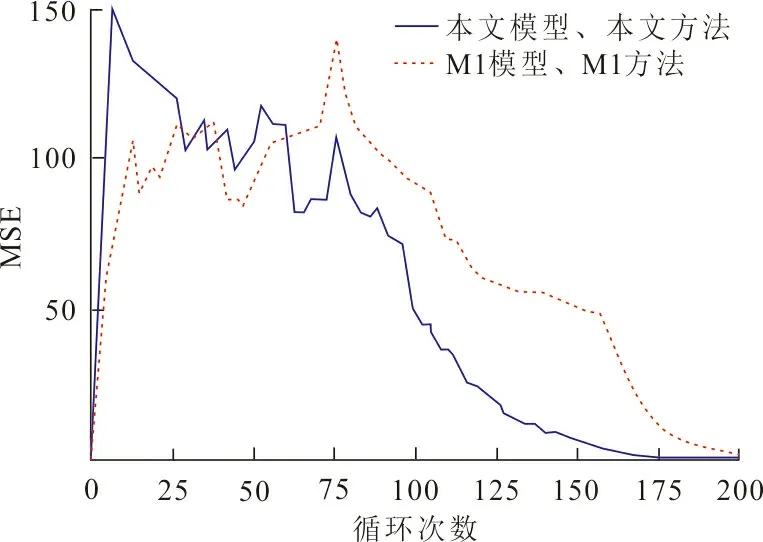
图 3 本文方法与M1方法的MSE对比图Fig.3 MSE comparison between the method in this paper and the M1 method
从图3可以看出,在25个飞行循环之前本文预测方法的误差明显高于M1方法。这是因为,由于本文方法退化模型的初始参数是随机的,因此在监测初期性能退化数据较少时,本文方法的MSE高于M1。在第25个飞行循环与第60个飞行循环之间,本文预测方法的MSE值与M1方法的MSE值接近。这是因为,随着飞行循环的增加、监测数据的增多,本文预方法的模型参数自适应更新使模型参数更加贴合实际情况。在过了65个飞行循环之后本文预测方法的预测误差明显低于M1预测方法,整体上看,本文预测方法的MSE值为13.25,M1预测方法的MSE值为16.12,说明本文预测方法有更高的预测精度,验证了它的有效性。
在此基础上,为验证所提模型的有效性,在2种模型上均采用M1方法估计未知参数,并进行航空发动机RUL预测,实验结果如图4所示。
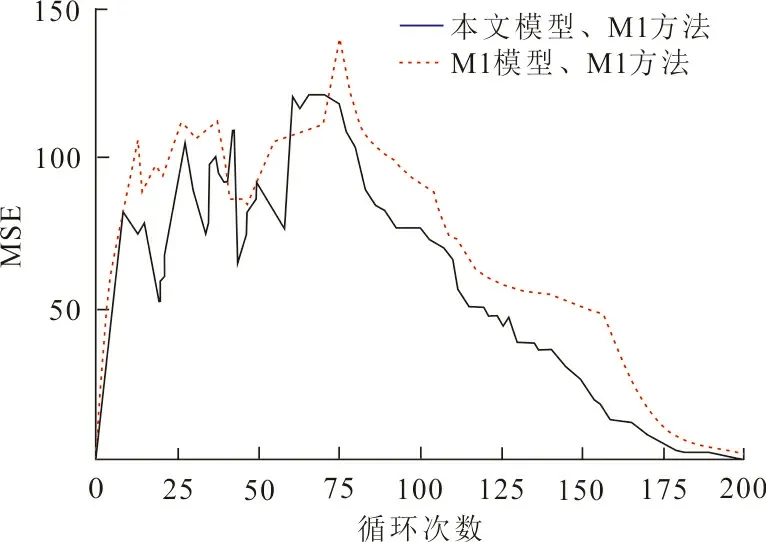
图 4 方法相同时2种模型的MSE对比图Fig.4 MSE comparison diagram of the twomodels when the methods are the same
从图4可以看出,在前10个飞行循环2种模型的预测精度接近,但10个飞行循环之后本文退化模型比M1模型具有更好的预测效果。应注意的是,在75个飞行循环附近,2种模型的预测误差均出现了上升趋势,这是因为在75个飞行循环附近,监测数据出现了异常值,影响了预测精度。但本文模型的预测精度高于M1模型的预测精度,说明本文模型能够有效地减弱监测数据异常值对预测精度的影响。从整体来看,本文模型比M1模型具有更高的预测精度,说明本文模型可以有效提高预测准确性。
接下来,为验证本文参数估计方法的优越性,采用本文模型作为退化模型,参数估计方法分别采用M1方法和本文方法,实验结果如图5所示。
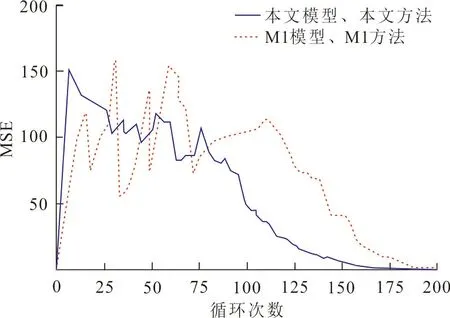
图 5 模型相同时2种参数估计方法的MSE对比图Fig.5 MSE comparison diagram of the twoparameter estimation methods when the models are the same
从图5可以看出,在退化模型相同时,使用本文参数估计方法进行RUL预测,具有更高的预测精度,同时,可看出本文参数估计方法可以提高预测模型的收敛速度和鲁棒性。
3 结 语
本文提出了一种考虑三源不确定性的Wiener过程航空发动机RUL预测方法。该方法将三源不确定性引入退化模型,且假设测量误差服从Logistics分布,能对测量误差较大的情况进行更好的拟合。在进行航空发动机RUL预测时,使用基于Spearman系数的关键参数筛选方法,筛选出对退化过程贡献更大的参数。然后,将基于最大熵无迹粒子滤波与ECM算法结合估计模型参数。在C-MAPSS数据集上的仿真实验,证明了该方法可以提高预测的准确性,可以提高航空发动机的使用率和可靠性。航空发动机的退化过程不仅普遍存在三源不确定性和非线性性,还存在多阶段的特点,在下一步研究中,应考虑航空发动机退化过程的多阶段性。

