Galerkin-Ivanov 变换的碰撞振动系统混沌运动
陈越超,冯进钤,王晓敏
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
非光滑动力系统是近年来国内外学者密切关注的问题之一,其中碰撞振动系统是常见的一类非光滑动力系统。在力学、机械学及机电工程、航空航天技术等实际系统中存在非光滑因素[1],例如电路系统的开关装置、机构运动的碰撞和干摩擦问题[2-3],走路机器[4]和状态反馈控制问题[5]等。以此建立的数学模型会表现出不连续或不可微的非线性动力学行为[6-7],比如系统的分岔和混沌运动[8-10]。 由于光滑动力系统理论无法应用于非光滑动力系统中,因此,对非光滑动力系统理论与近似方法的研究,是人们解决非光滑动力系统问题的有效途径。
HOLMES首次在碰撞振动系统中应用现代动力系统理论[11],随后SHAW等利用中心流形定理分析了碰撞振动系统的分岔现象[12]。文献[13]通过讨论Hopf分岔和不同形式的异宿轨道,分析了碰撞振动系统的混沌运动。混沌是非线性系统复杂性的重要特征之一,Lyapunov指数[14-16]是判别混沌运动的数值方法之一,而Melnikov、Shilnikov方法是研究混沌运动的2种解析法。 最初Melnikov方法主要用于光滑系统,后来DU等将Melnikov方法应用于倒立摆模型,进而将Melnikov函数推广到高阶[17]。 CAO等命名了SD振子,并通过Melnikov方法分析了系统的分岔和混沌现象[18]。 Melnikov方法通过计算稳定流形和不稳定流形之间的距离函数,得到系统存在简单零点的必要条件;根据Smale-Binkhoff定理,若存在简单零点,则系统具有Smale马蹄性质,从而可能出现混沌现象[19]。
本文用Melnikov方法研究一般的单边碰撞振动系统。首先利用Galerkin-Ivanov变换将系统模型转换为具有对称结构的光滑系统,然后通过光滑系统的Melnikov方法得到此系统出现Smale 马蹄混沌的必要条件,最后结合仿真实例验证了解析结果的正确性。
1 单边碰撞振动系统的Melnikov函数
考虑一般的单边碰撞振动系统,系统模型满足如下方程:
(1)
式中X>0。当X=0时,系统的状态满足如下离散映射:
(2)
式中:X和Y分别表示广义位移和速度;ε是一个小尺度参数;c(X,Y)表示系统的阻尼,b(X,Y,t)表示外激励;下标“+”和“-”分别表示碰撞前和碰撞后的时刻;r表示碰撞恢复系数,通常满足0≤r<1。令碰撞时刻为t*,则有Y±=Y(t*±0)。
引入Galerkin-Ivanov变换
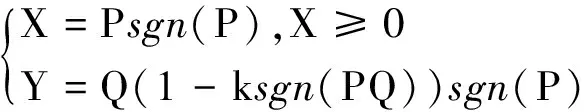
(3)
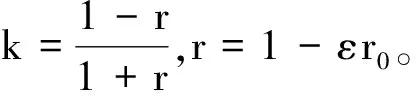
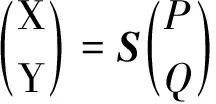
(4)
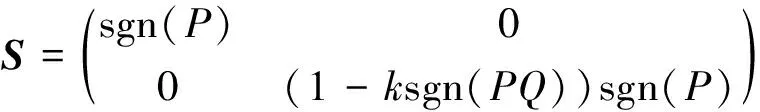
式(4)变形,得
(5)
将式(1)和(3)代入式(5),可得等价系统
(6)
当ε→0时,r→1,k→0,由Taylor公式展开,得
(1-ksgn(PQ))-1=1+εe+O(ε2)
(7)
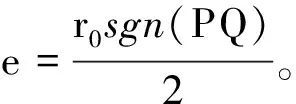
(8)
假设系统存在连接鞍点的同宿轨道Γ(t),其向量表示记为Γ(t)=(P(t),Q(t))T。由文献[20-21]知,等价系统的Melnikov函数可近似为
M(t)=-D1+D2-D3
(9)
式中:
sgn-1(P)|P=P(t),Q=Q(t)dt
(10)
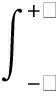
sgn-1(P)|P=P(t),Q=Q(t)dt
(11)
(12)
式中:D1为阻尼部分;D2为外激励部分;D3为碰撞部分。根据Smale-Binkhoff定理知,当Melnikov函数存在简单零点时,临界条件为
(13)
2 应用实例
考虑单边碰撞振动系统,系统满足方程
(14)
式中:X>0;β为系统的阻尼系数,f为外激励的幅值。
当X=0时,系统的离散碰撞映射为
(15)
基于式(3)中的Galerkin-Ivanov变换,将式(14)代入式(8),得到系统(14)的近似等价方程
(16)
当ε=0时,系统(16)为一个未扰系统
(17)
当P>0时,未扰系统(17)的势函数和Hamilton函数分别为
(18)
(19)
由动力学稳定性理论知,此时未扰系统(17)存在一个中心S(0,0)和一个鞍点S1(1,0)。 连接鞍点S1(1,0)的同宿轨为
Γ+(t)=(P+(t),Q+(t))T
其表达式为
Γ+(t)=(P+(t),Q+(t))T=
(20)
其中
(21)
(22)
当P<0时,同理,未扰系统(17)的势函数和Hamilton函数分别为
(23)
(24)
同理可知,系统有一个中心S(0,0)和一个鞍点S2(-1,0)。 连接鞍点S2(-1,0)的同宿轨为
Γ-(t)=(P-(t),Q-(t))T
其表达式为
(25)
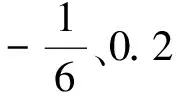
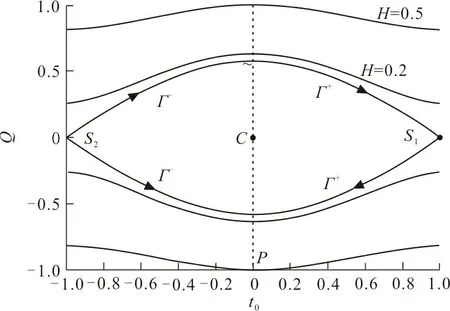
图 1 未扰系统的同宿轨Fig.1 The homoclinic orbits of the unperturbed system
由文献[20-21]可知,系统Melnikov函数的一阶近似式为
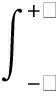
sin(ωt+ωt0)+
e(P2sgn(P)-P)]|P=P±(t),Q=Q±(t)dt
(26)
分2种情况讨论系统的Melnikov函数。当P>0时,由式(10)~(12)得
(27)
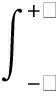
Q|P=P+(t),Q=Q+(t)dt=
f[cos(ωT0)Z1(ω)-
sin(ωT0)Z2(ω)]cos(ωt0)
(28)
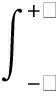
(29)
其中
(30)
(31)
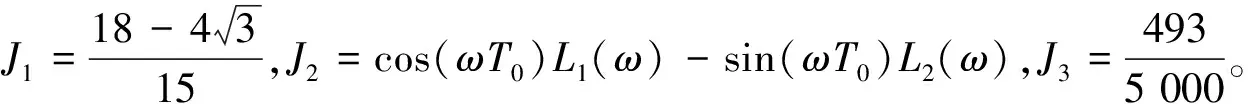
M1(t0)=-βJ1+fJ2cos(ωt0)+r0J3
(32)
同理,当P<0时,由式(10)~(12)得
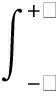
(33)
(34)
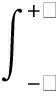
(493/5 000)r0
(35)
系统的Melnikov函数一阶近似式为
M2(t0)=βJ1-fJ2cos(ωt0)-r0J3
(36)
根据式(32)和(36)知,M2(t0)=-M1(t0),故系统(1)出现Smale马蹄混沌的必要条件为
f≥(βJ1-r0J3)/J2
(37)
3 数值仿真
利用数据仿真直观的说明式(32)和(36)结论的正确性。由于系统是对称的,只讨论M1(t0),同理可以仿真M2(t0)。固系统参数ω=1,β=0.6,ε=0.1,r0=1.55,当式(37)取等号时得到阈值f~≈0.268,M1(t0)的函数曲线如图2所示。将M1(t0)的函数曲线局部放大得到图3。在图3中,3条曲线f1、f2、f3取值分别为f1=0.2
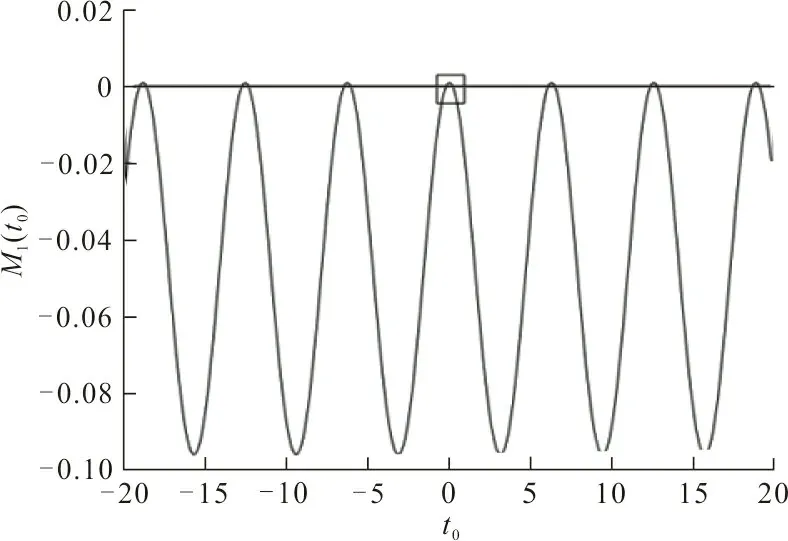
图 2 M1(t0)随时间t0变化的函数曲线Fig.2 Function curve of M1(t0) with time t0
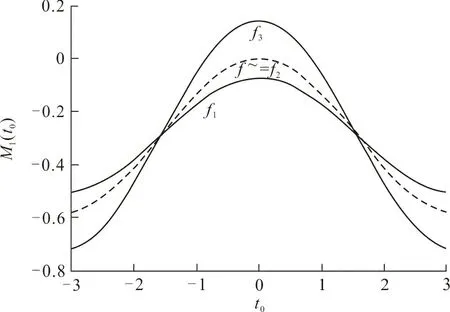
图 3 f取不同值时对应的M1(t0)函数曲线Fig.3 Function curve of M1(t0) when f takes different values
从图3可以看出:当f1=0.2
进一步验证式(37)的解析结果。 当式(37)取等号时,得出系统(14)出现混沌的临界线,如图4所示。图4中,线下表示非混沌区域,线上表示可能的混沌区域。
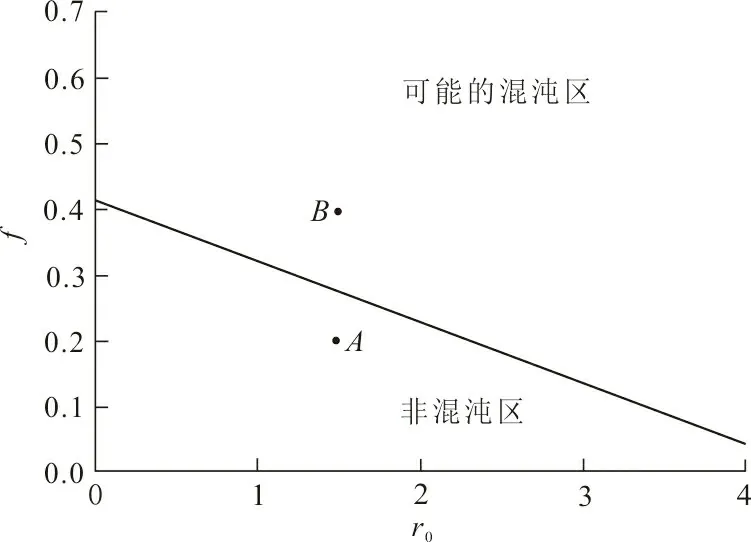
图 4 f随r0变化的Melnikov临界线Fig.4 Melnikov critical boundary of fvarying with r0
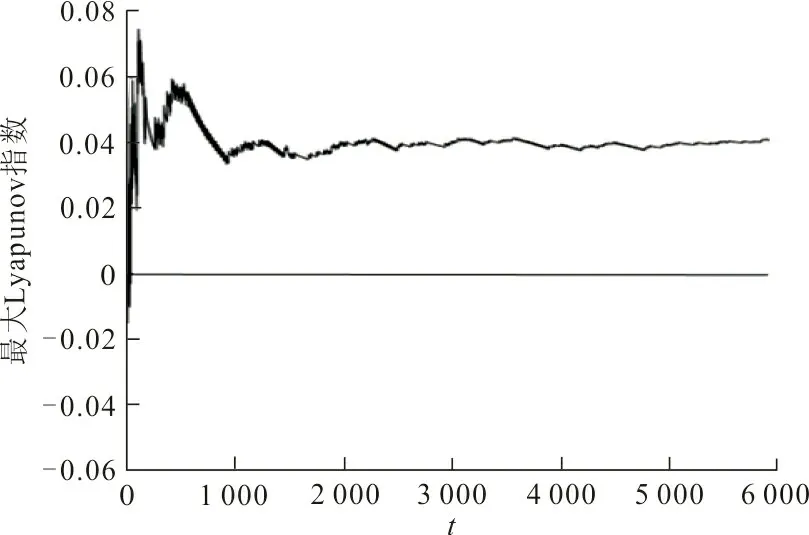
取临界点(r0,f~)以下的点A(1.55,0.2)及临界点以上的点B(1.55,0.4)进行仿真验证,结果如图5、6所示。
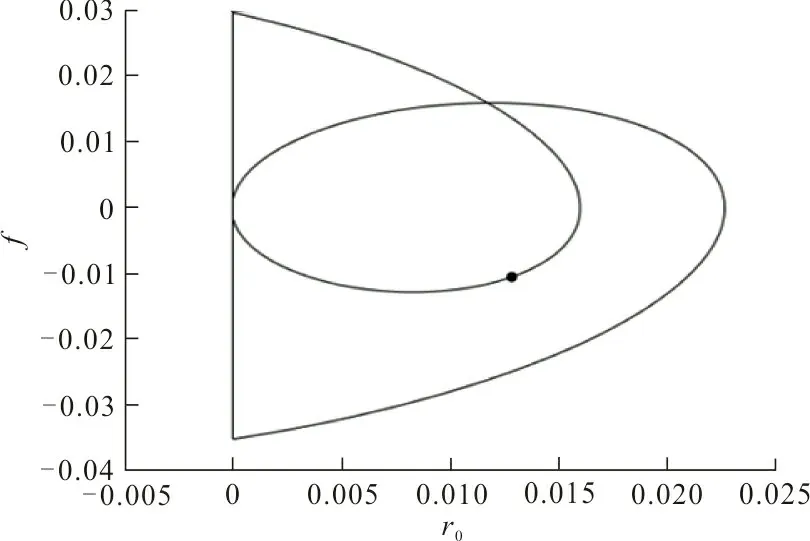
(a) 相图、Poincare截面图
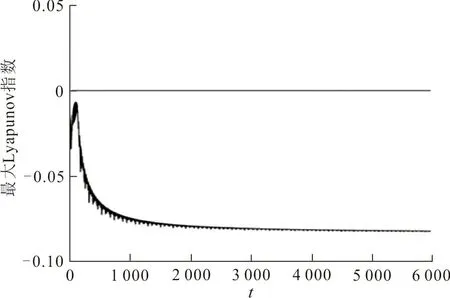
(b) 最大Lyapunov指数序列图 5 f=0.2时的相图、Poincare截面图及最大Lyapunov指数序列Fig.5 Phase diagram,Poincare section and sequence diagram of maximum Lyapunov exponent (f=0.2)
当f1=0.2 同样由Melnikov理论知,当f=0.4>f~时,对应图4中的B点,图6(a)给出了系统的相图、Poincare截面图。从图6(a)中可以看出,此时系统的运动变得杂乱无序,并计算其对应的最大Lyapunov指数λB≈0.28>0,见图6(b)。进一步表明在B点参数情况下系统作混沌运动,同样与图4所示结果一致。 (a) 相图、Poincare截面图 (b) 最大Lyapunov指数序列图 6 f=0.4时的相图、Poincare截面图及最大Lyapunov指数序列Fig.6 Phase diagram,Poincare section and sequence diagram of maximum Lyapunov exponent (f=0.4) 本文通过Galerkin-Ivanov变换将碰撞振动系统转化为等价的光滑系统,并基于光滑系统的Melnikov方法判断非光滑系统的混沌运动。然后,以单势阱碰撞振动系统为研究实例,基于Galerkin-Ivanov变换构建了系统的Melnikov方法,得到了系统出现Smale马蹄混沌的必要条件。通过数值仿真验证了解析结果的正确性,表明了该方法的有效性。为碰撞振动系统的混沌运动的研究提供有效途径。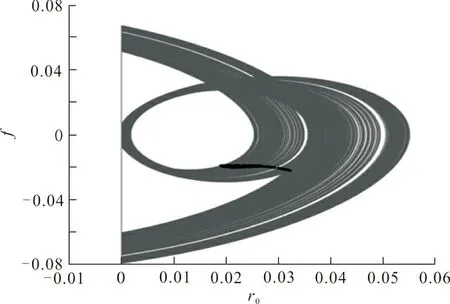
4 结 语

