战术无人机视距下行通信链路信道模型特性的研究
邓海峰,申江江,何勰,刘旭宁,吴一
(海军航空大学91206部队,山东 青岛 266000)
随着航空技术的高速进步和人工智能技术的发展,无人军事装备在现代战争及非战争军事行动中应用越来越广泛,在作战侦察及反恐等领域获得了长足的发展。无人机(Unmanned Aerial Vehicle,UAV)凭借其灵活性高、使用方便、机载配置多样化等特点得到了越来越多的应用和重视。随着目前无人机搭载侦查设备日渐多样化,载荷不断提高,其下行通信链路需要传输的信息种类不断增多,对其数据传输速率提出了更高的要求。为了提高无人机数据传输速率,必须对其通信链路进行分析,通信链路信道特性是提高通信传输速度的基础问题[1-3]。无人机下行链路信道除了具有无线通信基本特点之外,兼具低仰角地空通信链路信道和移动通信信道特点,比一般的无线信道更加复杂,研究战术无人机下行链路的信道特征,进而建立准确的信道模型,对于提高战术无人机作战使用效能具有重要作用[4-5]。
1 无人机无线移动信道的传播特性
无人机移动信道本身属于无线电波,在空中传播过程中受到空间环境各种因素的影响,表现出多种衰落特征,比如收发两端带来的路径损耗,信号传输中会受到反射及散射等影响,一般可以将对信道的影响区分为大规模衰落和小规模衰落[6]。
1.1 无线信道大规模衰落模型
大规模衰落通常表现为通信目标大范围移动造成的路径衰落和平均信号能量的衰减,这是无线通信领域中最普遍的损耗形式。Hata根据Okumura的应用测量结果,总结出了路径损失的参数方程,根据不同的应用场景选择其数学表达式可以表示为[7]:
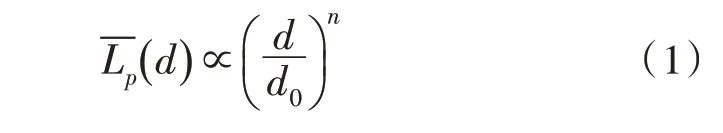
按照dB形式可以写为:
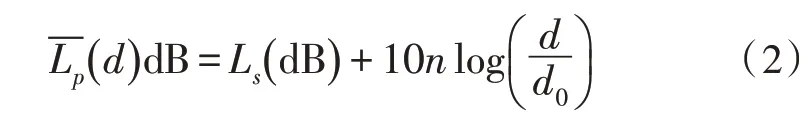
其中,d为信号传输距离,d0为参考距离(远离发射天线的一个位置和天线之间的距离,可选1 km、100 m、1 m)。路径损耗指数n由信号频率、天线位置和传输的环境条件等决定,一般情况下当信号在空间中进行传播时n取2即可,如果信号在街道等可能存在波导现象的空间中传播时n可能会小于2,当传播路径中存在障碍物时n可能会增大。
1.2 无线信道小规模衰落模型
在工程实践中基站位置安排、发射功率设置等工作中小规模衰落是需要考虑的关键问题,研究调制方法的应用时主要关注点也在于小规模衰落。小规模衰落是信号在较小距离或较短时间内幅值、相位剧烈的动态变化,具体表现为两种形式:信号的时延扩展和信道的时变特性。信号时延扩展是由信道多径干扰引起的,信号传播过程中受到反射、散射等多种原因,到达接收端的时间不同,因此,接收端就会收到不同时延信号的叠加,由于不同反射路径的信号幅度、相位、入射角各有不同,使叠加而成的接收信号幅度、相位产生失真[8-11]。
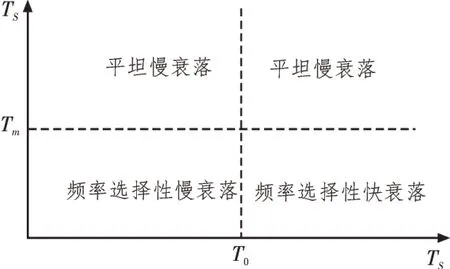
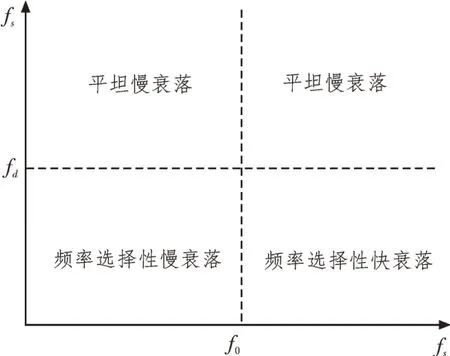
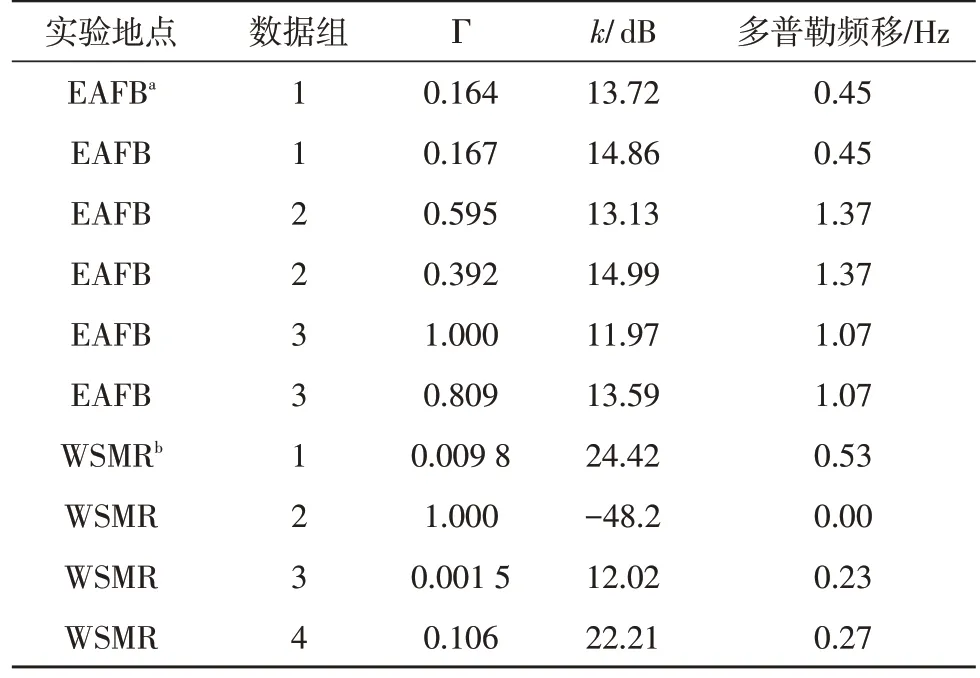
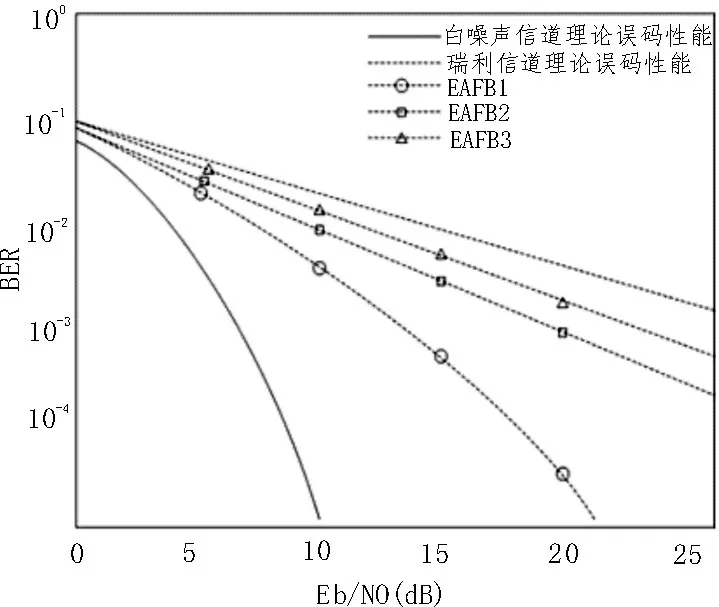
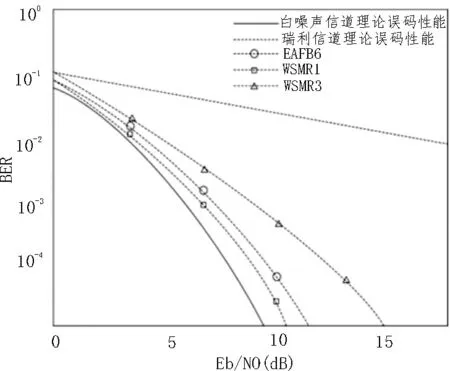
根据最大超量时延Tm和码元时间Ts的关系,时延扩展造成的性能下降分为频率选择性衰落(Frequency–selective Fading)和平坦衰落(Flat Fading)两种类型。若Tm 信道的时变性是由发射机与接收机相对移动或信道内物体的运动引起的,当发射机与接收机相对运动时,接收信号受多普勒效应的影响,产生频率偏移,多普勒效应产生的频率偏移表示为: 其中,fc是发射信号载频,v是发射机与接收机相对运动速度,φ为相对运动方向与电波入射方向夹角,c为光速。 根据多普勒频移fd与信号带宽fs的关系,可以将信道分为快衰落信道和慢衰落信道。当fs>fd时,信道呈现慢衰落特性,信道特性在一个码元持续时间里保持不变。当fs 由上述分析可知,为使信号在无线移动信道传输过程中不发生频率选择性失真和快衰落失真,必须综合考虑信号的时延扩展和信道的时变性。在时域表现为信号码元持续时间Ts时需满足Tm 图1 信道衰落特性随信道码元时间变化规律 图2 信道衰落特性随信道带宽变化规律 根据战术无人机平时执行任务要求,其飞行速度较低,容易满足Ts 由于战术无人机地面站设有高增益的定向天线,下行链路信道存在一个较强的直视信号。同时,信号传输过程中存在反射与散射现象,因此,战术无人机下行链路信道属于低测控仰角的航空信道。早期的航空信道研究并没有提出明确的数学模型,自Bello提出了多普勒频谱表达式后[12],相关的研究逐渐增多。文献[13]建立了航空下行通信链路的数学模型,其系统带宽为5 MHz,并且指出信道的莱斯因子介于2~20 dB之间。Hass E在总结前人工作基础上,针对航空信道建立了时域抽头延迟线模型,该航空信道模型由一个较强的直视分量和若干散射分量构成[11-15]。 无人机在起飞/降落时测控仰角较大,信号强度较大,多径干扰最小,信道近似为高斯白噪声,通信质量好。随着距离增大,测控仰角逐渐变小,进入接收端的地面反射波能量增大,由于定向天线的存在,信号包含直视分量,信号包络服从莱斯分布: 其中,直视分量与散射分量的能量比为莱斯因子k: 当测控仰角进一步减小,接收机就不会接收到明显的直视分量,信号包络会服从瑞利分布: 由上述分析可知,战术无人机下行链路信道随着无人机与地面站距离的增大,测控仰角逐渐减小,信道特性由高斯白噪声逐渐变化为瑞利信道。 莱斯在对不同场景信道参数进行实测的基础上,将信道模型具体为直视分量、反射分量、散射分量组成的三径模型[14],其冲击响应为: 式中,t、τ表示特定时刻和时间增量,a0、a1、ε(t)分别为直视分量、地面反射波分量和散射分量的幅度,Δθ1是反射分量相对视行分量的相移,Δωd1和Δωd2分别是反射分量和散射分量的多普勒频移。由于OFDM子载波信号带宽相对较小,一般而言小于信道相干带宽,属于窄带信号,而对窄带信号而言,式(7)可以化简为: 当a1=0时,信道简化为莱斯信道。该模型即可作为战术无人机下行链路信道模型,即无人机下行信道模型为加入反射分量的莱斯信道,相比两径模型,三径模型将地面强反射分量单独计算,更加符合低仰角的战术无人机信道模型。文献[14]给出了航空信道的两个重要参数k、Γ,用以描述信道反射分量与散射分量的大小,并对信道进行了实测,视行分量与散射分量能量的比值为莱斯因子k,参数Γ为反射分量与视行分量幅值比: 其中,δd为散射分量ε(t)的方差。 文献[14]对信道参数进行了测量,数据结果如表1所示(a为爱德华空军基地,b为白沙导弹试验场)。 表1 航空信道参数 由表1可知,Γ一般在0.2~0.8之间变化,k一般在10~20 dB之间变化。 无人机飞行过程分为3个主要状态,即起飞/降落状态、途中飞行状态和任务区域盘旋状态,不同飞行状态下信道参数的典型值如表2所示[10],文献[15]提出了一种最大时延扩展的估计方法,当飞行距离远大于飞行高度时,地空链路最大时延扩展近似为飞行高度与光速比值h/c。由于没有文献实测战术无人机飞行过程中的信道时延扩展值,该文以h/c为信道时延扩展值进行研究,战术无人机飞行高度一般在100~4 500 m间变化,可知多径时延变化范围约为0.33~15μs。 表2 不同飞行状态下信道参数 为研究反射分量对于信道特性的影响,以64点FFT(N=64)的OFDM系统为例,研究该系统通过航空下行信道后BER性能分析航空信道特性[16-18]。 首先选择散射分量能量接近、反射分量能量差距较大的EAFB数据组1、2、3进行研究,系统误码性能如图3所示。 图3 反射分量能量差距较大时误码性能比较 从图中可以看出,当散射分量相近、反射分量差距较大时,系统BER性能有明显差距,当反射分量幅值较大时系统性能接近瑞利信道理论值,当反射分量幅值较小时系统性能接近高斯白噪声信道理论值。 然后选择反射分量能量系数接近且幅值较小、散射分量能量差距较大的EAFB数据组6与WSMR数据组1、3进行研究,系统误码性能如图4所示。 图4 散射分量能量差距较大时误码性能比较 从图中可以看出,反射分量能量系数接近且幅值较小、散射分量能量差距较大时,系统误码性能区别并不明显,且误码性能接近高斯白噪声信道误码性能。 通过上述分析可知,航空下行传输信道主要受反射分量支配,当反射分量较大时,信道特性接近瑞利信道,反射分量较小时,信道特性接近高斯白噪声信道。相比之下,将反射分量单独描述的三径模型更能反应无人机下行链路信道特性,适合无人机下行链路信道建模。 该文分析了战术无人机无线移动信道的传播特点,对下行链路信道的几种典型衰落模型及其各自特点进行了分析。在信道研究基础上,以常见的OFDM通信系统为例,对实测航空信道参数进行误码性能分析,得出航空下行传输信道主要受反射分量支配的结论,当反射分量较大时,信道特性接近瑞利信道,反射分量较小时,信道特性接近高斯白噪声信道。通过上述分析为战术无人机信道建模提供了参考借鉴,对于建立准确的战术无人机下行信道模型,提高战术无人机作战效能具有重要作用[19-20]。
1.3 无线信道小规模衰落信道特性
2 战术无人机下行通信链路信道模型特性分析
2.1 战术无人机信道模型分析
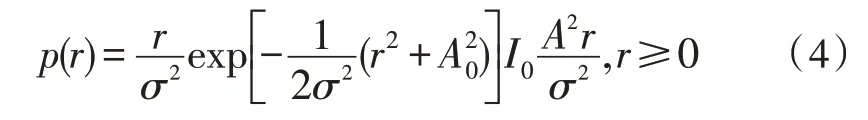

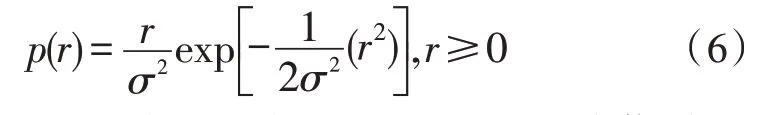
2.2 战术无人机下行信道模型
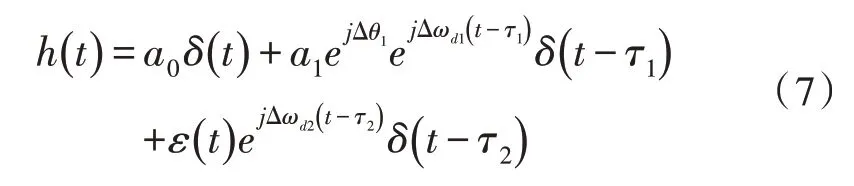
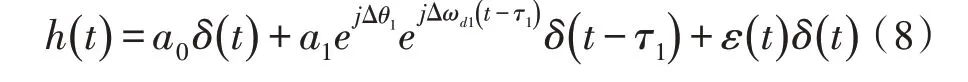
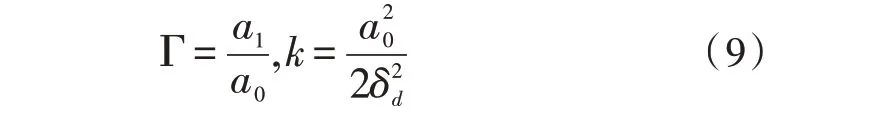

2.3 战术无人机信道模型分析
3 结束语

