基于定向变异遗传算法的智能组卷算法研究

胡新源，赵当丽，李 辉，张向波，韩振兴

（1.中国科学院国家授时中心，陕西 西安 710600；2.中国科学院大学，北京 100049；3.中国人民解放军63768部队，陕西 西安 710600）

随着在线考核在现代教学方式中占比逐渐增大，实现准确、高效的智能组卷算法已成为现代教育研究的一个热点。文献[1-2]对几种智能算法应用在组卷问题上的性能做出了比较，目前解决组卷问题主要依赖遗传算法[3-4（]Genetic Algorithm，GA），但是由于组卷问题数学模型较复杂，导致基于标准遗传算法（Standard Genetic Algorithm，SGA）的组卷算法存在明显寻优能力弱、易早熟收敛陷入局部最优等GA常见问题。文献[5]根据组卷约束条件人为选取初始种群，提高初始种群的适应度。文献[6-8]提出混合遗传算法以提升算法性能，文献[9]提出一种自适应遗传算法（Adaptive Genetic Algorithm，AGA），通过自适应调整交叉变异概率提升组卷效率。但是以上优化对于遗传算法的性能提升均有限。文献[10]提出一种定向变异遗传算法（Directional Variation Genetic Algorithm，DVGA）的思想，对算法性能提升取得较好的效果。为进一步改善GA的寻优能力，该文基于以上研究基础，结合组卷模型进一步加强算法的定向寻优能力，同时降低了组卷时间，具有良好的性能。

1 智能组卷数学模型构建

组卷算法的目的在于根据给出的限制条件，从题库中自动抽选符合条件的试题组卷，其数学本质是在多维约束条件下求全局最优解问题[11],。解决此类问题需要确定一个目标函数及多个约束条件，在组卷问题中，约束条件即为题目的各项属性，因此每道试题可以通过一维向量Q=(a1,a2,a3,…,an)来描述，n表示每道试题需要被约束的属性总数。包含m道试题的题库则构成一个m×n的矩阵D[12]，如下所示：

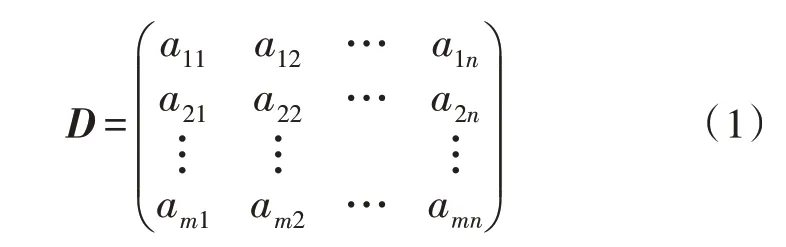
组卷的过程即为从题库矩阵D中选取一个满足各约束条件的子集矩阵的过程，该组卷模型将以难度、章节、曝光时间、题型、分数5个属性作为约束条件，各属性约束和目标函数的选取如下所示。

1）难度：试卷的难度约束应为试卷各试题的平均难度，用于区分考生水平。

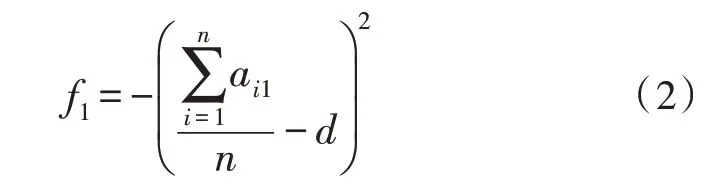
式（2）中，ai1表示第i题的难度值，d表示预期的试卷整体难度，n表示该试卷中题目总数。

2）章节：章节用于约束试卷考察知识范围，需对试卷逐题判断是否属于目标章节。

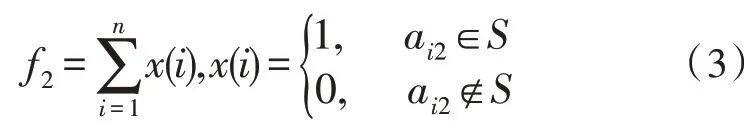
式（3）中，ai2代表第i题的考察章节，S代表指定的章节范围。

3）曝光时间：曝光时间表示该题目距离上次被抽取用于组卷的间隔时长，需逐题判断，用于避免题目频繁出现。

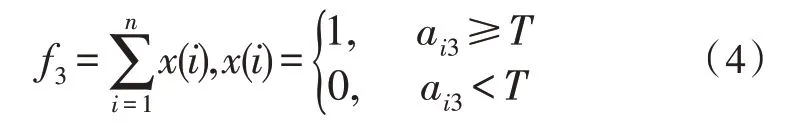
式（4）中，ai3表示第i题的曝光时间，T代表最低未被组卷使用的间隔次数。

4）题型：通常试卷的题型结构是固定且可枚举的，需逐题判断整卷的各题型是否符合指定数量。

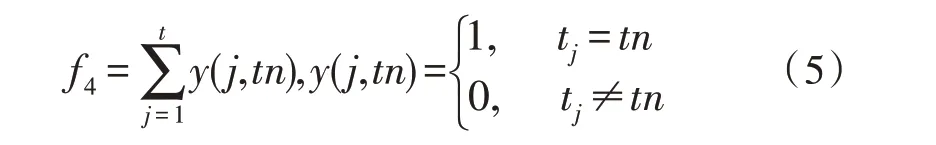
式（5）中，t代表试卷中总题型数，tn代表每个题型的预设数量，tj为形如f2的函数，用于统计试卷中各题型数量，tj中以ai4代表第i题的题型。

5）分数：分数属性需要统计整卷所有试题分数求和，且应允许一定的误差。

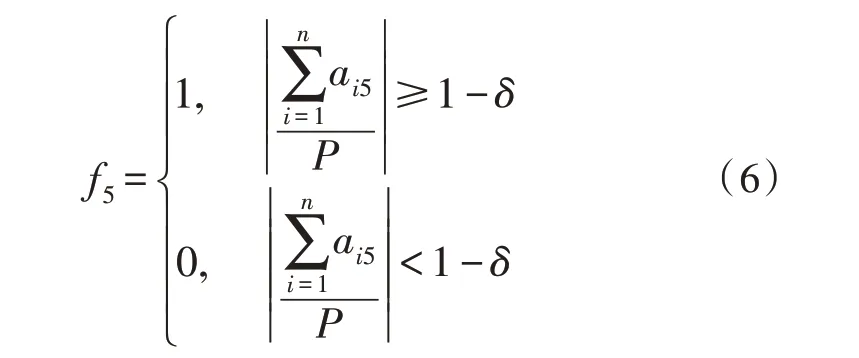
式（6）中，ai5代表第i题分数，其中P为预设试卷总分数，δ为可接受的误差范围。

2 基于遗传算法的组卷

GA被广泛应用在组卷问题中，具体思路为：针对组卷问题进行基因编码、适应度函数的设计，选取合适的遗传算子后即可抽取一定数量的试卷作为初始种群，进行选择交叉变异，直到种群中最优个体满足指定条件。种群中最优个体即为满足约束的目标试卷。

2.1 基因编码

GA中种群中的个体需用基因编码表示，通常采用二进制编码来描述个体[13]。当应用在组卷问题时，个体的基因编码即为试卷所包含的试题编号，若采用二进制编码时，题库中的每个题都需要出现在编码中，极大地浪费了编码效率。其次，在每次交叉变异的过程中需对试题题型进行判断，引入了大量计算。文献[14]提出一种实数分段式编码，以试题编号实数为基因，按试题题型分段编码，如下所示。

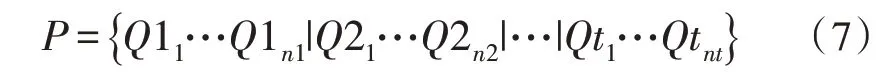
式（7）中，Qi表示试卷中的第i种题型，共计t种题型，每种题型ni道。采用实数分段式编码时，基因编码长度仅为试卷试题总数，极大提升了编码效率，且各题型在试卷染色体中位置固定，因此在交叉操作中可省略对题型的判断[15]，如图1所示。

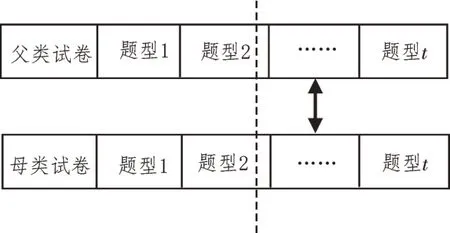
图1 采用实数分段式编码的交叉操作

2.2 适应度函数

适应度函数用来评判个体的优劣性，应满足单值、非负及合理反映个体优劣程度等要求，根据已建立的组卷模型可知适应度应为各项约束条件求加权和。

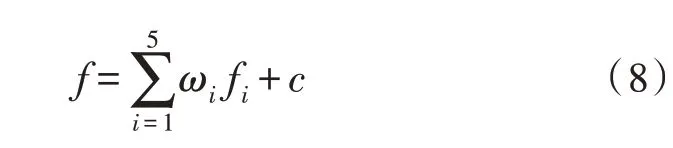
上式中，c用于保证目标函数的非负性，ωi表示各项约束条件在目标函数中的权重。其中，。

2.3 初始种群选取

根据已建立的组卷模型可知，组卷约束条件分为难度、题型、分数等需要统计整卷判断和章节、曝光时间等逐题判断两种类型。由于目标试卷中每道试题必定满足第二类需逐题判断的约束条件，因此当确定约束条件后，可根据指定的章节及曝光时间对题库进行筛选形成基因库G。结合编码结构的题型设置，从中抽取一定数量的试卷作为初始种群，可使得初始种群有一个较高的适应度，加速算法收敛。

2.4 遗传算子设计

GA中的遗传算子分为选择算子、交叉算子、变异算子三部分。

选择算子控制着进化过程中的筛选作用，为了符合优胜劣汰的规律同时又不丧失种群物种多样性，通常采用轮盘赌方法。同时为了避免最优个体在进化过程中丢失，采用精英策略保留当代最优个体，使最优个体无需经过选择交叉及变异直接进入下一代。

交叉算子用于模拟种群进化过程中的繁衍过程，通常采用单点交叉的方式，通过选择算子选取父母个体以交叉概率Pc进行交叉。

变异算子用来模拟种群进化过程中个体产生基因突变的情况，用于维持种群的多样性，决定了算法的搜索能力，通常采用单点变异，种群中个体以概率Pm进行变异，由于组卷模型存在题型约束，因此变异结果应从同题型试题中抽取。

2.5 终止条件

组卷即为求适应度函数最大值的过程，当种群中最优个体达到指定要求或达到指定的进化次数后停止进化，最优个体即为满足预设目标的试卷。

3 基于定向变异遗传算法的组卷

3.1 遗传算子的改进

GA中交叉概率Pc和变异概率Pm对于算法寻优能力和收敛速度有着重要影响，自AGA被提出以来，众多优秀的改进自适应遗传算法陆续被提出[16]，该文采用基于Sigmoid曲线改进的自适应遗传算子来进一步提升算法寻优能力。

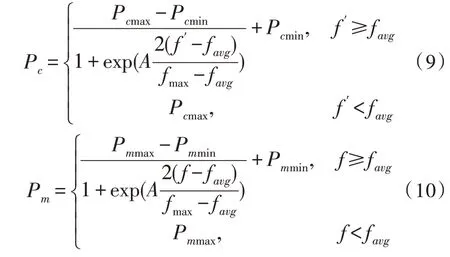
上式中，A=9.903 438，Pcmax、Pcmin表示交叉概率最大值及最小值，Pmmax、Pmmin表示变异概率最大值及最小值，f′表示进行交叉的父母个体中较大的适应度，favg表示当代种群平均适应度，fmax表示当代种群最大适应度，f表示发生变异个体的适应度。

3.2 变异操作的改进

根据前文实数分段式编码结构及GA流程可知，在一次完整的组卷过程中，交叉操作只会改变各试卷的试题组合，而不会从总题库中抽取新的试题，仅在变异操作过程中会引入新的试题。因此，从基因库G中抽取试题作为变异结果，可确保由变异操作产生的新试题，在章节及曝光时间等需逐题判断的约束条件下直接满足目标。且由于初始种群也在基因库G中选取，因此在一次完整的组卷过程中，种群个体的基因即各试题始终满足章节及曝光时间等需逐题判断的约束条件，适应度函数中关于章节及曝光时间的权重系数ω2、ω3可置为0，从而可以使得该组卷模型从五维约束条件简化为三维约束条件。

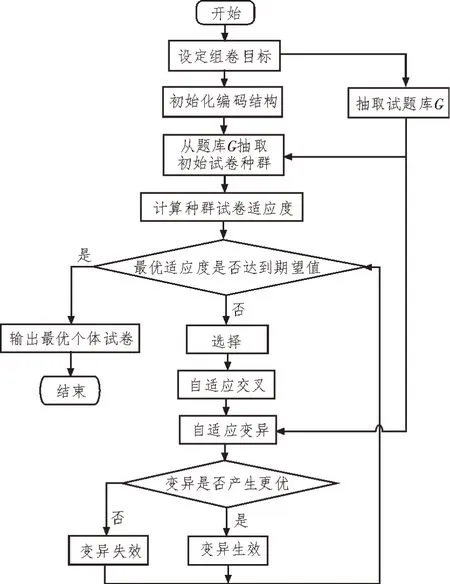
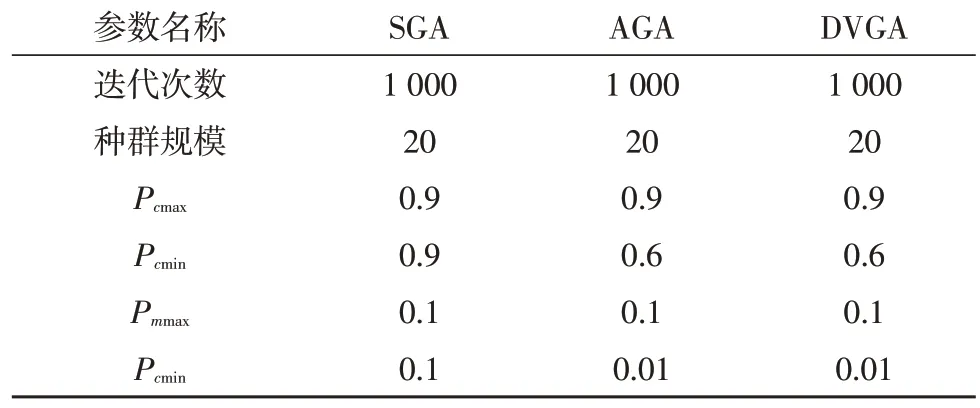
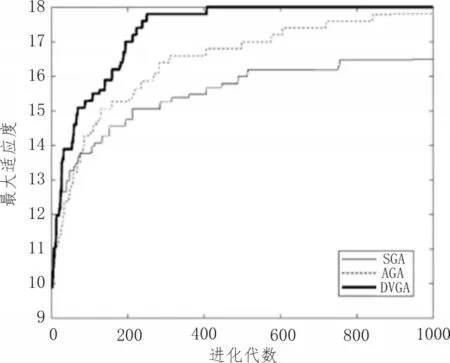
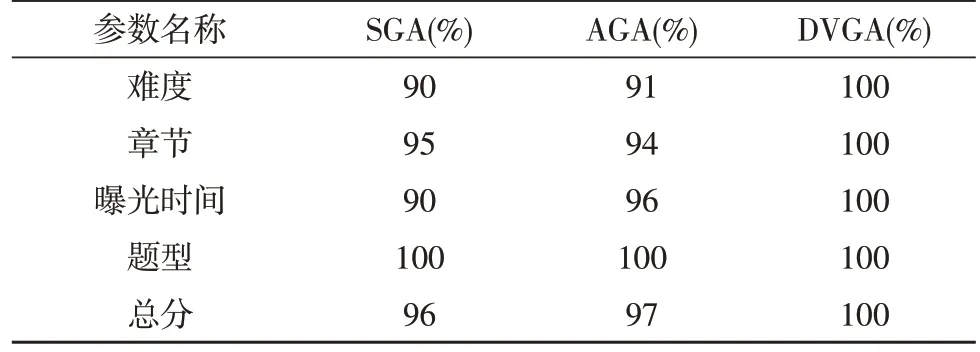
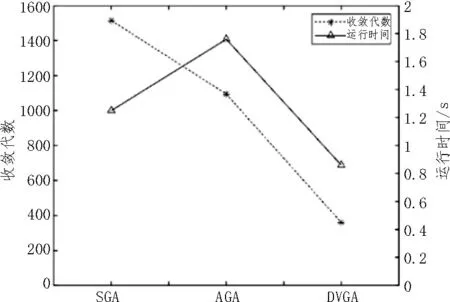
由于GA基于优胜劣汰的法则，当种群进化到中后期往往存在严重同化现象即陷入局部最优，此时由于种群同化严重，交叉操作已几乎不能产生新试卷个体，主要依赖变异产生优良试卷个体跳出局部最优，而随机变异会使得种群在长时间内无法跳出局部最优。因此需对变异方向加以控制，使其只能朝着更优定向变异。定向变异是指当发生变异时，计算发生变异个体变异前的适应度f(x)与变异后的适应度f′(x)，仅当f(x)

基于以上约束目标属性及适应度的DVGA的组卷算法，不仅缩小了组卷过程寻优的搜索空间，同时还限定了变异方向，使得个体只能朝着全局最优发生变异，种群更易跳出局部最优，极大地提升了算法的寻优能力，同时简化了组卷过程的计算量，从而提升了组卷效率。

3.3 改进遗传算法

基于上述对遗传算子和变异操作过程的改进，可得到基于DVGA的组卷算法流程如图2所示。

图2 基于DVGA的组卷算法流程

4 仿真验证

为了验证文中提出的基于DVGA的组卷算法对组卷性能的提升，进行如下实验，设置参数如表1所示。

表1 参数设置

结合上述流程图进行编程仿真，可以得到在相同条件下，各算法最大适应度如图3所示。

图3 3种算法种群最大适应度比较

同时，以表1条件进行20次试验，分别对SGA、AGA、DVGA平均组卷准确率、收敛代数及运行时间进行比较，可得到表2及图4结果。

表2 3种算法组卷准确率比较

图4 3种算法收敛代数及算法耗时

从图3可以看出，该文提出的DVGA相比于AGA及SGA，具有更强的寻优及跳出局部最优的能力。表2及图4表明，该文提出的DVGA准确率及组卷效率相较于SGA及AGA均取得较大的提升。

5 结束语

智能组卷问题本质是对多约束多目标的问题寻求最优解。该文充分利用组卷模型中约束条件的特性，优先筛选出带有部分最优特性的优良基因库，使变异从中产生且定向只可朝着最优变异，极大地缩短了组卷时间，提高了组卷效率。