行波效应下混凝土V形折板网壳地震响应分析
姜腾钊,张华刚*,魏威3,马克俭
(1.贵州大学空间结构研究中心, 贵州 贵阳 550003;2.贵州省结构工程重点实验室, 贵州 贵阳 550025;3.贵州建工监理咨询有限公司, 贵州 贵阳 550081)
0 引言
混凝土曲面壳施工时,节点坐标控制不准是引起结构几何初始缺陷的重要原因[1],因此张华刚等[2]将曲面壳与密肋平板结合,提出了混凝土折板式网壳结构,经工程实践证明,结构具有较好的技术经济指标[3]。考虑到我国是一个地震多发国家,并且随着城市化进程的加快和经济的高速发展,地震所造成的损失和影响在成倍增长[4]。国内一些学者对混凝土折板式网壳的动力特性和抗震性能进行了初步研究[5-7],但采用的是地面运动的一致输入,而对于大跨度结构,地震动的空间变异性对结构的影响不容忽视[8-10],其中行波效应对结构影响更为显著[11],因此一致输入下的地震反应分析难以对结构的抗震性能进行充分的估计,本文采用有限元大质量法[12],考虑行波效应,对混凝土折板式网壳进行了X向地震激励和三向地震激励下结构的地震反应分析,揭示了结构在行波效应的影响下内力分布的特点,旨在定量分析行波效应对结构受力性能的影响。
1 结构模型概况

1.密肋梁;2.横向脊线拱;3.横向谷线拱;4.纵向脊线拱;5.屋面板;6.空腹桁架上弦;7.空腹桁架腹杆;8.空腹桁架下弦;9.纵向框架柱;10.抗推结构;11.山墙框架柱;12.山墙框架梁;13.天沟图1 结构形式Fig.1 Structure form
结构形式如图1所示,主结构由横向脊(谷)线拱和纵向脊线拱构成,密肋平板支承在主结构上,纵向脊线拱为多折拱。纵向框架柱顶需设空腹桁架等边缘结构封闭拱脚,山墙处可设框架结构支承屋盖。由于本文仅分析屋盖自身的地震响应,因此不计天沟、支座抗推结构及山墙框架的影响。
本文算例的基本情况如图2所示,结构跨度为52.00 m,纵向长度为54.00 m,支座间距为18.00 m,每块密肋平板的周边均沿屋盖跨度方向等分为8个网格、纵向等分为5个网格,结构平面布置如图2(a)所示。密肋平板斜放,网格构造如图2(b)所示。拱脚处设空腹桁架,如图2(c)所示,顶点高度即结构纵向矢高为f2=2.00 m。屋盖剖面如图2(d)所示,结构横向矢高为f1=9.00 m。纵向脊线拱截面尺寸为0.30 m×0.55 m,横向脊(谷)线拱截面尺寸为0.40 m×0.60 m,V形拱脚空腹桁架腹杆、下弦杆截面尺寸均为0.40 m×0.40 m,空腹桁架上弦截面尺寸为0.40 m×0.50 m,密肋梁截面尺寸为0.25 m×0.35 m,屋面板厚度取为0.10 m 。有限元建模按自然节点划分单元,屋面板为空间板壳单元,除屋面板外的构件均采用空间梁单元。计算时混凝土的弹性模量取为E=3×104N/mm2,泊松比为v=0.2。阻尼采用瑞雷阻尼,结构阻尼比取为0.05,并假定结构所处地区的抗震设防烈度为7°,地震分组为第二组,场地类别为Ⅱ类。

(a) 结构平面图
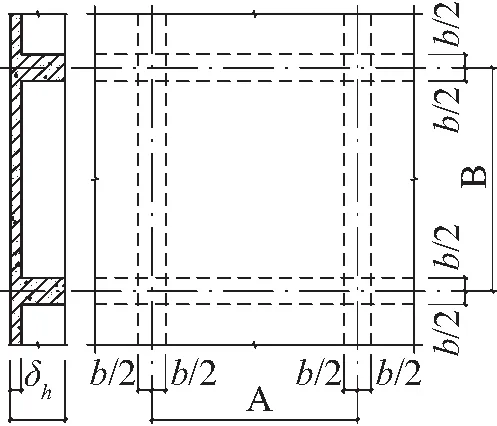
(b) 密肋板网格构造

(c) A-A视图

(d) B-B剖面图
2 模态分析及地震波的选取
利用商业有限元软件,对结构进行模态分析,得到结构前10阶自振频率见表1,结构的前6阶振型如图3所示。由图3可以发现,1至6阶振型表现为集中于横向拱的振动,且山墙处的振型位移相较于其他区域的振型位移更为明显,而工程应用时,此处至少有山墙框架与屋盖柔性连接,结构的薄弱位置已得到加强;地震波采用适用于中软场地的El-Centro波[13],结构的基本周期约为0.5 s,时间步长取为0.02 s,持时取14 s,为结构基本周期的28倍,已满足地震波时长要求。依据结构所处位置为7°区,对El-Centro波加速度时程曲线进行等比例缩放,调整后的地震加速度时程曲线峰值为35 cm/s2。进行三向地震激励输入时,按1(水平主向X)∶0.85(水平次向Y)∶0.65(竖向)的比例进行调幅[14],同时假定地震波沿结构X正方向传播。

(a) 第1阶

(b) 第2阶

(c) 第3阶

(d) 第4阶

(e) 第5阶
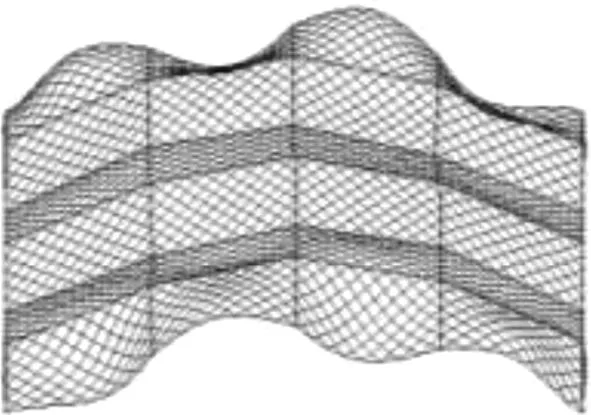
(f) 第6阶
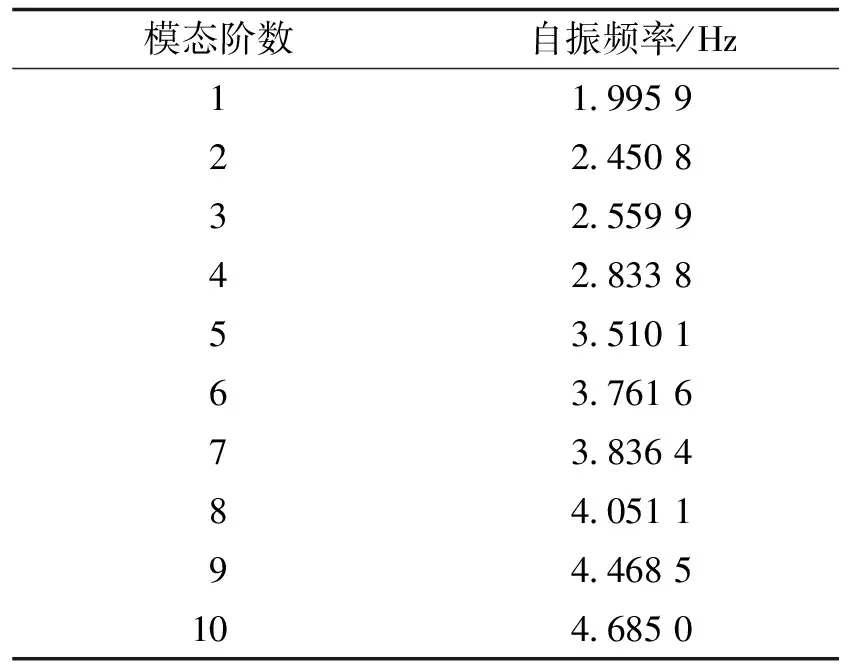
表1 结构前10阶自振频率Tab.1 Top 10 natural frequencies of structure
3 结构的地震反应分析
采用大质量法对结构进行一致地震输入和考虑行波效应的多点地震输入的地震响应分析,通过对不同视波速下的结构内力进行对比,来探讨行波效应对混凝土V形折板网壳的影响,并定义地震输入影响系数[15]ε为
(1)
式中,Nt为行波输入下的构件内力;Nc为一致输入下的构件内力。结果讨论时,将忽略由于杆件自身动内力较小而导致ε值过大的截面。由于结构构件数量较多,同种构件仅选取具有代表性的构件进行分析,选取的构件及截面编号于图2(a)标出,纵向脊线拱与空腹桁架上弦截面编号相同。Ⅱ类场地视波速V的范围为100~500 m/s[16],因此在进行计算时,分为4种工况,分别为:视波速100 m/s,视波速200 m/s,视波速500 m/s,一致输入。
3.1 X向地震激励
图4为横向谷线拱L3在不同视波速下的弯矩分布图,由图4可以看出,行波输入下横向谷线拱梁支座附近和弯折处的弯矩明显大于一致输入,当视波速为200 m/s和500 m/s时,ε值较为接近,介于1.1~1.6,当视波速为100 m/s时,弯矩会急剧增大,ε值介于2.1~3,表明横向谷线拱与纵向脊线拱交点位置受行波效应的影响较为显著。横向谷线拱的其他位置则受行波效应的影响相对较小,3种视波速下的ε值集中于0.9~1.6,其中当视波速为200 m/s时,行波效应使横向谷线拱跨中区域的弯矩小幅降低。
图5为纵向脊线拱L2在不同视波速下的弯矩分布图,从图5可以发现,纵向脊线拱在靠近横向谷线拱区域及跨中区域受行波效应影响较小,视波速为100 m/s时,ε值在1~1.6;视波速为200 m/s时,ε值在0.6~1;视波速为500 m/s时,ε值在0.9~1.7。而靠近横向脊线拱区域受行波效应影响明显,视波速为100 m/s时,ε值在1.9~2.3;视波速为200 m/s时,ε值在1~2;视波速为500 m/s时,ε值达到了1.3~1.8。综上所述,当视波速较低时,行波效应对构件的影响会更为显著。

图4 横向谷线拱L3的弯矩分布Fig.4 Bending moment distribution of main arch
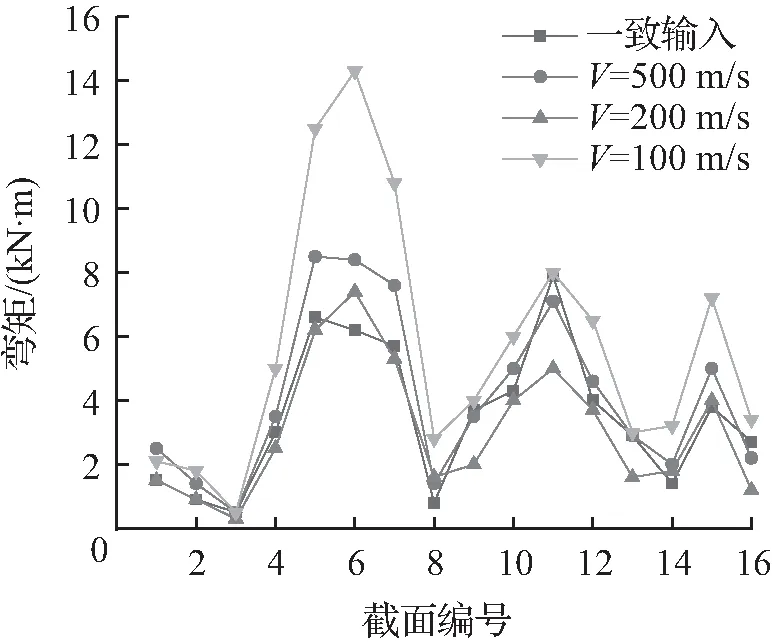
图5 纵向脊线拱L2的弯矩分布Fig.5 Bending moment distribution of ridge
密肋梁和空腹桁架上弦的弯矩分布情况分别如图6和图7所示。从图6中可以看出,密肋梁靠近支座位置的截面,在视波速为100 m/s时的弯矩明显大于一致输入下的弯矩,ε值在2~3.1,视波速为200 m/s和500 m/s时,ε值在1~1.6,其他截面的ε值在3种视波速下差值不大,集中在0.4~1.3;从图7中可以看出,空腹桁架上弦与支座相连区域受行波效应影响明显,ε值在1~5.7,其他截面在几种工况下弯矩非常接近,ε值介于0.7~1.2。

图6 密肋梁L4的弯矩分布Fig.6 Bending moment distribution of rib

图7 空腹桁架上弦L1的弯矩分布Fig.7 Bending moment distribution of side beam
图8为横向谷线拱L3在不同视波速下的轴力分布图,由图8可知,横向谷线拱的所有截面在行波输入下的轴力均大于一致输入下的轴力并且行波效应对横向谷线拱两端的影响相较于跨中位置更为明显。其中视波速为200 m/s和500 m/s时,构件的轴力较为接近,端部区域大部分截面的ε值在1.1~1.7,当视波速降低至100 m/s时与一致输入的差异明显增大,ε值达到了2.3~3.1,而越靠近跨中位置,3种视波速下的轴力越接近,说明横向谷线拱的跨中位置对视波速的改变并不敏感。
图9为纵向脊线拱L2在不同视波速下的轴力分布图,从图9中可以发现,在视波速为200 m/s时纵向脊线拱的轴力均小于一致输入时构件的轴力。与横向谷线拱相交区域的轴力接近一致输入下构件的轴力,ε值在0.5~1.3,纵向脊线拱和横向脊线拱相交区域的轴力与一致输入下构件的轴力相差较大,ε值处于0.6~1.7。

图8 横向谷线拱L3的轴力分布Fig.8 Axial force distribution of main arch

图9 纵向脊线拱L2的轴力分布Fig.9 Axial force distribution of ridge
图10为密肋梁在不同视波速下轴力的分布情况,从图10中可以看出,视波速为100 m/s时,密肋梁的轴力最大,而视波速为200 m/s和500 m/s时,轴力与一致输入工况相比差距较小。视波速为100 m/s时,支座附近截面的轴力在明显大于一致输入,ε值在2.5~2.7,但越靠近横向脊线拱位置,与一致输入的差值逐渐减小,ε值介于1.2~1.7。视波速为200 m/s和500 m/s时,支座附近截面的轴力略大于一致输入,ε介于1.1~1.5,与横向脊线拱相接位置的轴力小于一致输入下构件的轴力,ε值介于0.4~1.0。
图11为空腹桁架上弦在不同视波速下轴力的分布情况,支座附近的构件截面受行波效应影响明显,随着视波速的降低,与一致输入结果的差值增加,但ε值的分布没有规律,1#至6#截面和10#、11#截面在3种视波速下的ε值集中在1~2.9,轴力大于一致输入的情况。其余截面在3种视波速下的ε值集中在0.4~1,轴力小于一致输入工况。

图10 密肋梁L4的轴力分布Fig.10 Axial force distribution of rib

图11 空腹桁架上弦L1的轴力分布Fig.11 Axial force distribution of side beam
综合上述分析可以发现,随着视波速的降低,构件的内力先减小后增大,且当视波速较低时,行波效应对结构的地震响应影响更为显著。行波效应对结构的影响主要集中在支座附近、纵向脊线拱与横向脊线拱的交汇位置,而越远离上述区域,行波效应的影响越弱。此外受行波效应影响较小的区域对视波速的变化也不敏感。行波效应对结构动力响应的影响因区域而异,部分区域内力增大,部分区域内力减小。
3.2 三向地震激励
通过对三向地震激励和X向地震激励下4种类型的构件的弯矩分布情况进行对比可以发现,两种情况下行波效应对结构的影响情况基本相同,同样表现为:支座附近位置、纵向脊线拱与横向脊线拱的交汇位置以及横向谷线拱的跨的弯折部位,在行波输入下的内力明显大于一致地震输入,受行波效应影响显著,越远离上述区域,在行波输入下的内力越接近一致地震输入的内力,受行波效应影响相对较小。视波速为100 m/s时构件的内力最大,与一致输入的情况差异最为明显,表明视波速较低时,行波效应对结构的影响最为显著。在行波效应的影响下,部分区域的内力会增加,部分区域的内力会降低。
两者差异则表现为:4种类型的构件在三向地震激励时的弯矩均大于水平地震作用下的弯矩,但差异不大。与X向地震激励的情况相比,4种类型的构件在三向地震激励下受行波效应影响更为显著。例如从图12至图15中可以发现,横向谷线拱支座附近和弯折位置的地震输入影响系数ε在视波速200 m/s和500 m/s时,范围为1.3~2,当视波速为100 m/s时,ε值则达到了2.4~3.2。横向谷线拱的其他位置在3种视波速下的ε值集中在0.7~1.7;当视波速为100 m/s和500 m/s时,纵向脊线拱与横向谷线拱相交区域的ε值在0.9~1.7,而与横向脊线拱相交区域的ε则达到了1.9~2.3;当视波速为200 m/s时,与横向谷线拱相交区域的ε值在0.6~1.2,与横向脊线拱相交区域的ε值在1.1~2.3。密肋梁与支座相连位置截面的ε值在1.1~3.3,其余截面的ε值介于1.2~2.4;空腹桁架上弦与支座相连位置受行波效应影响较为显著,地震输入影响系数ε值在1.3~6.9,明显大于一致输入的情况,其余受行波效应影响较弱区域的地震输入影响系数ε在0.8~1.8。

图12 横向谷线拱L3的弯矩分布Fig.12 Bending moment distribution of main arch
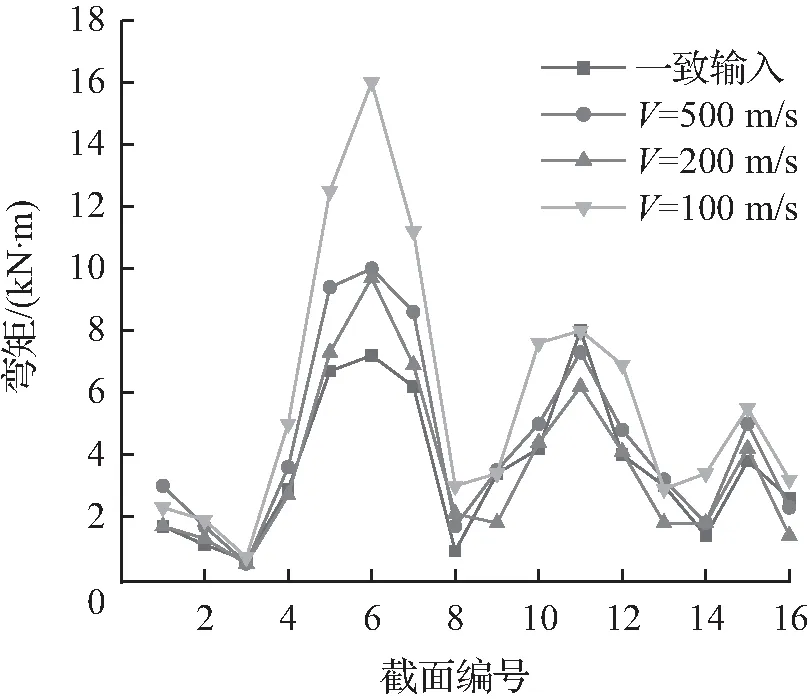
图13 纵向脊线拱L2的弯矩分布Fig.13 Bending moment distribution of ridge

图14 密肋梁L4的弯矩分布Fig.14 Bending moment distribution of rib

图15 空腹桁架上弦L1的弯矩分布Fig.15 Bending moment distribution of side beam
对比图8与图16可知,在X向地震激励下与三向地震激励下,横向谷线拱在4种不同工况下的轴力分布情况类似,但横向谷线拱的轴力在三向地震激励下更大,支座位置的差异尤其明显,当视波速为100 m/s时,横向谷线拱的ε值达到了1.7~3.5,当视波速为200 m/s和500 m/s时,ε值则在1.1 ~2.6。与X向地震激励相比,随着视波速的降低,ε增加更为明显,说明在三向地震激励下,行波效应对横向谷线拱的影响更为显著。
通过对比图9和图17可以发现,纵向脊线拱在X向地震激励下与三向地震激励下的轴力值和分布情况均非常接近。纵向脊线拱与横向谷线拱相交区域的轴力接近一致输入下构件的轴力,ε值在0.6~1.4,纵向脊线拱与横向脊线拱相交区域的轴力与一致输入下构件的轴力相差较大,ε处于0.7~1.8,两种地震激励下的地震输入影响系数基本相等。由此说明,两种不同方向的地震输入下,对构件的轴力几乎没有影响,并且行波效应对纵向脊线拱影响程度相同。
图18为密肋梁在三向地震激励下4种工况的轴力分布情况,与X向地震激励时的轴力分布情况基本相同,但行波效应的影响程度有差异。当视波速为100 m/s时,支座附近区域的地震输入影响系数明显小于X向地震激励的情况,ε值在1.8~2。视波速为200 m/s和500 m/s时的地震输入影响系数则在1.0~1.4,与X向地震激励时的ε值较为接近。当视波速为100 m/s时,与横向脊线拱相接位置的ε值在1.4~1.5;当视波速为200 m/s及500 m/s时,靠近横向脊线拱的位置,ε值在0.6~1.1。与X向地震激励对比可以看出,三向地震激励下,视波速为100 m/s的地震输入影响系数明显小于X向地震激励的情况,与其他类型的构件情况相反。
图19为空腹桁架上弦在三向地震激励下4种工况的轴力分布情况,与X向地震激励时的轴力分布情况基本相同,但三向地震激励下构件的轴力明显大于X向地震激励时的轴力。1#~6#截面和10#、11#截面在3种视波速下的ε值集中在0.9~3,与X向地震激励相比差异较大,其余截面在3种视波速下的ε值集中在0.5~1,轴力小于一致输入的情况,与X向地震激励时的地震输入影响系数基本相同。
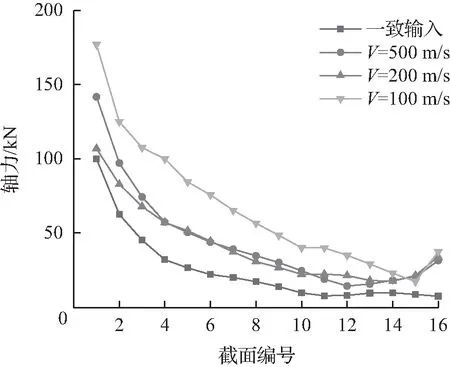
图16 横向谷线拱L3的轴力分布Fig.16 Axial force distribution of main arch

图17 纵向脊线拱L2的轴力分布Fig.17 Axial force distribution of ridge

图18 密肋梁L4的轴力分布Fig.18 Axial force distribution of rib

图19 空腹桁架上弦L1的轴力分布Fig.19 Axial force distribution of side beam
综合上述分析,在三向地震激励下,行波效应对结构的影响与在X向地震激励下的情况基本相同,但也存在差异,其不同点在于,三向地震激励下构件的内力略大于X向地震激励下构件的内力,并且除密肋梁外,构件在三向地震激励下受行波效应影响更为显著。
4 结论
选用El-Centro波,对混凝土V形折板网壳结构分别进行了X向地震激励和三向地震激励下的地震反应计算,对两种情况进行了对比,揭示了混凝土V形折板网壳受行波效应影响的特点,并对不同视波速下构件节点的内力结果进行了讨论,可得到以下结论:
① 随着视波速的降低,构件的内力呈先减小后增大的趋势。
② 视波速较低时,行波效应对结构的影响更为显著。
③ 行波效应对结构的影响主要集中在支座附近和纵向脊线拱与横向脊线拱的交汇位置。在做抗震设计时可对不利区域截面的内力乘上地震输入影响系数。
④ 行波效应对结构动力响应的影响因区域而异,因此在做抗震设计时需要进行具体分析。
⑤ 三向地震激励下,行波效应对结构的影响与在X向地震激励下的整体趋势基本相同。
⑥ 三向地震激励下构件的内力大于X向地震激励下构件的内力,但差值较小,说明水平地震反应控制抗震设计,除密肋梁外,构件在三向地震激励下受行波效应影响更为显著。

