碳纳米管混凝土桥墩抗震性能有限元分析

李振东,孙敏

(苏州科技大学 土木工程学院， 江苏 苏州 215011)

0 引言

随着我国经济的稳步发展，各种中大型桥梁的建设在不断地进行，一旦发生地震，那么必将对桥梁结构，特别是对桥墩会带来很大的影响。碳纳米管作为纳米级纤维材料，加入到混凝土中制成的碳纳米管混凝土，不仅可以提升混凝土的自收缩和抗裂性能[1]，还可以提升混凝土材料的力学性能[2]。

近些年来，国内外很多学者对碳纳米管混凝土的性能进行了大量的研究。申若虚[3]系统地研究了不同掺量的碳纳米管水泥砂浆的性能，结果表明：各掺量的碳纳米管均可以提高水泥砂浆的抗压、抗折强度，且0.3%掺量的碳纳米管水泥砂浆性能达到最优。PARVEENS等[4]采用新型分散技术制备了碳纳米管增强水泥复合材料并进行了一系列试验，发现与普通砂浆相比，碳纳米管增强复合材料的缺口试件弯曲试验显示出更好的延性。为了进一步研究碳纳米管混凝土墩柱的性能，EFTEKHARI等[5]研究碳纳米管混凝土柱在服役荷载作用下的力学性能和延性，发现在混凝土柱中添加碳纳米管可以显著提高其吸能能力。PAPADOPOULOS等[6]对碳纳米管加固的混凝土的RVE分层结构进行了有限元模拟，实现碳纳米管混凝土模拟方法的改进，此外，所提出的计算多尺度分析策略可以准确有效地预测具有复杂微观结构的材料的行为，并且可以替代部分实验。由于碳纳米管的掺入，提高了混凝土材料的力学性能、延性等，但目前并没有将碳纳米管混凝土运用到具体结构并研究其抗震性能。为此，笔者通过有限元模拟的方法来研究碳纳米管混凝土桥墩抗震性能有着十分重要的意义。

1 碳纳米管混凝土本构关系

1.1 碳纳米管混凝土分析理论

目前，对纤维混凝土主要的分析方法有量子力学、分子动力学、连续介质力学。在连续介质力学基础发展而来的损伤理论[7-9]，主要研究内部裂缝发展对其本构关系的影响，该理论能够详细地描述混凝土材料的力学性能，进而估算出结构的使用寿命以及它的安全可靠性。因此，在有限元分析过程中，纤维混凝土本构模型[10]选用损伤本构模型[11]。

1.2 基于分子结构力学的等效连续体模型

碳纳米管作为纳米量级材料，自身尺度非常小，有限元模型的建立比较困难。相较于量子力学和分子动力方法[12]，连续介质力学的方法虽然没有考虑到原子尺度的影响，但是它不受尺度的限制，并且可以通过有限元软件来实现计算。

目前来说，常用的连续介质模型一般有梁模型、壳模型、桁架模型以及分子结构力学模型。LI等[13]利用分子结构力学模型建立了碳纳米管的有限元模型，并验证了该模型的可行性。但对于碳纳米管混凝土材料来说，这样的模型不能完全反映碳纳米管作为一种增强材料在水泥基材料中的作用机理，程远征[14]建立了碳纳米管材料的基于分子结构力学的等效力学模型，研究了更加复杂的碳纳米管力学性能，为连续介质模型模拟提供了可靠的参数依据。王德刚[15]根据分子结构力学模型计算模拟了碳纳米管的杨氏模量，并在此基础上将其等效为连续体，建立碳纳米管的等效连续体模型，并得出了等效连续体模型的弹性常数。本文选取其得到的弹性常数E=523.4 GPa，泊松比μ=0.165。

2 碳纳米管混凝土本构关系确定

2.1 混凝土塑性损伤参数

在进行ABAQUS数值模拟分析时，采用混凝土塑性损伤模型前要进行塑性损伤模型参数的确定，本文采用的C30混凝土ABAQUS塑性参数取值可以参考表1。

表1 C30混凝土塑性模型破坏准则参数Tab.1 C30 concrete plastic model failure criterion parameters

2.2 混凝土本构关系选取

本文采用与实例桥墩相同的C30混凝土，本构关系采用《混凝土结构设计规范》(GB 50010—2010)的混凝土本构关系。

2.3 碳纳米管混凝土代表体积单元

碳纳米管属于微观结构，若考虑整个碳纳米管混凝土模型，则计算量十分巨大，难以进行。为此相关学者引入了代表体积单元的概念，即选取一个微元代表整个结构，通过代表微元分析整个复合材料，代表体积单元的尺寸由增强相的选取数量及试件增强相与基体的体分比等确定。为了使选取的微元能够代表复合材料，需要保证微元的本构关系等价于复合材料的本构关系、微元内的增强相足够多，所以微元需要满足三个条件：①所选取的微元尺度要远远小于结构尺度；②选取的微元尺度要大于增强相的尺度；③微元内增强相的体分比要等于结构内增强相体分比。

碳纳米管采用多壁碳纳米管，主要参数见表2。

表2 碳纳米管主要物理参数Tab.2 Main physical parameters of carbon nanotubes

选取碳纳米管最优掺量[16]为0.3%，并换算成体分比为0.5%，微元内碳纳米管数量为5，碳纳米管直径为70 nm，长度为250 nm，经过计算得到微元长度为987 nm，利用多尺度非线性复合材料建模平台digimat建立微元模型，碳纳米管随机投放，并导入ABAQUS中，最后建立的碳纳米管混凝土代表体积单元模型如图1所示。

图1 碳纳米管混凝土代表体积单元Fig.1 Carbon nanotube concrete represents volume unit

2.4 碳纳米管混凝土单轴拉压模拟

对碳纳米管混凝土代表体积单元进行单轴受力模拟，得到其单轴拉伸应力-应变曲线和单轴压缩应力-应变曲线，如图2所示。

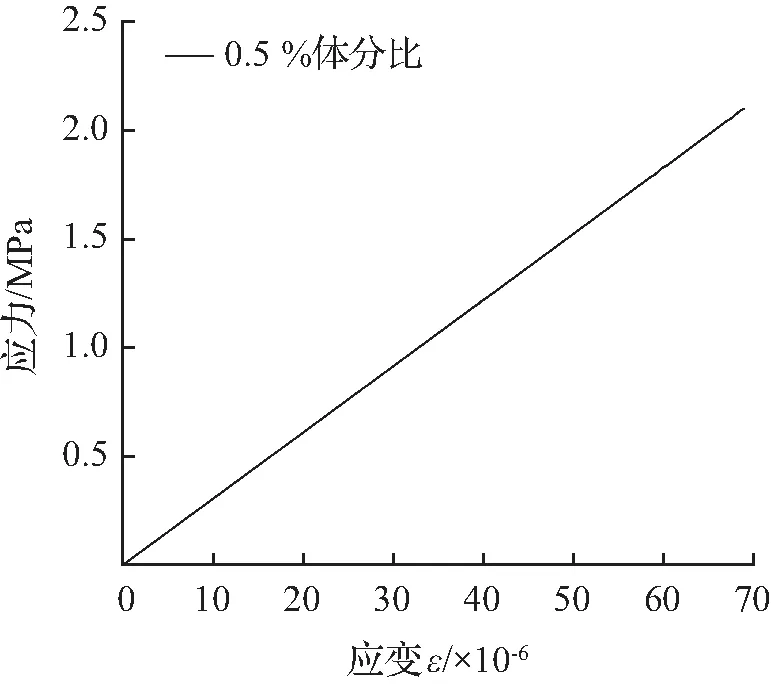
(a) 单轴拉伸应力-应变关系

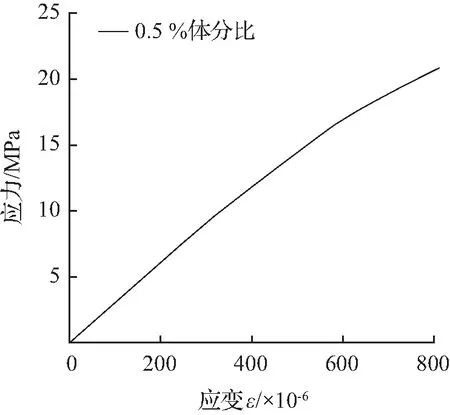
(b) 单轴压缩应力-应变关系

从图2(a)可知，碳纳米管混凝土抗拉强度极限值为2.1 MPa，相比于普通混凝土轴心抗拉强度极限值2.01 MPa，提高了4.5%。说明碳纳米管的掺入可以提高混凝土的抗拉强度，这是由于碳纳米管的抗拉性能高、延性好，在混凝土内部可以起到很好的桥联作用。从图2(b)可知，碳纳米管混凝土抗压强度极限值为20.85 MPa，相比于普通混凝土轴心抗压强度极限值20.1 MPa，提高了3.7%。说明碳纳米管的掺入可以提高混凝土的抗压强度，这是由于碳纳米管是纳米级，可以很好地减小混凝土内部的孔隙，使得混凝土更加密实。

2.5 碳纳米管混凝土本构关系公式

利用Origin软件将C30混凝土本构关系与碳纳米管混凝土单轴受力曲线进行拟合，对C30混凝土本构关系中的参数进行修改。

碳纳米管混凝土单轴受拉模型如下：

(1)

(2)

式中，

αt=0.312ft,r2;Ec为C30混凝土弹性模量;ft,r、εt,r分别为碳纳米管混凝土单轴抗拉强度和对应的混凝土峰值拉应变，取ft,r=2.1 MPa，εt,r=6.9×10-5。

碳纳米管混凝土单轴受压模型如下：

(3)

(4)

式中，

αc=0.157fc,r0.785-0.905;Ec为C30混凝土弹性模量;fc,r、εc,r分别为碳纳米管混凝土单轴抗压强度和对应的混凝土峰值压应变，取fc,r=20.85 MPa，εc,r=8.12×10-4。

对碳纳米管混凝土单轴受力曲线进行拟合，结果如图3所示。

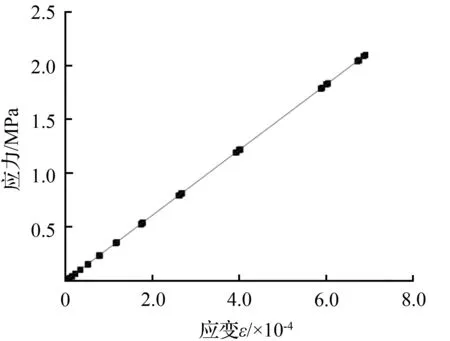
(a) 单轴受拉应力-应变曲线拟合

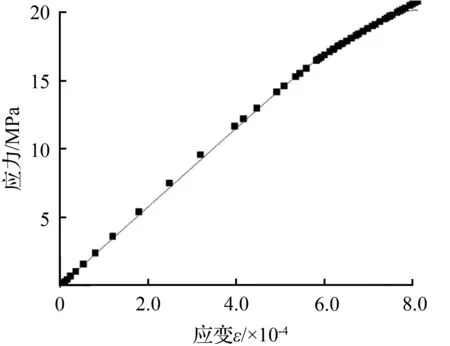
(b) 单轴受压应力-应变曲线拟合

通过曲线拟合，确定取参数A=1.5，B=0.002，得到碳纳米管混凝土单轴受拉损伤因子和应力-应变公式如下：

(5)

(6)

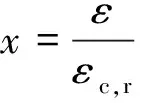
(7)

(8)

2.6 碳纳米管混凝土本构关系验证

为了进一步验证模拟得到的碳纳米管混凝土本构关系的正确性，现通过实际试验进行比较，实际案例选用同课题组0.3%掺量碳纳米管混凝土抗折试验。碳纳米管混凝土抗折试验仪器如图4所示，碳纳米管混凝土试块尺寸为100 mm×100 mm×400 mm。采用三组试块取其抗折强度平均值。

通过ABAQUS后处理得到碳纳米管混凝土抗折强度为5.13 MPa，试验得到的三组抗折强度平均值见表3，发现模拟值要小于试验值，两者误差为4.1%。所以通过ABAQUS模拟得到的碳纳米管混凝土本构关系具有一定的合理性。

图4 碳纳米管混凝土抗折试验Fig.4 Carbon nanotube concrete bending test

表3 碳纳米管混凝土试验抗折强度数据Tab.3 Flexural strength data of carbon nanotube concrete test

3 碳纳米管混凝土桥墩有限元模拟

3.1 桥墩有限元模型的建立

本文以宜兴市新渎港桥为例，该桥为一座三跨钢筋混凝土连续梁桥。选取全桥非线性较高的桥墩来进行有限元模拟分析，建立的桥墩模型如图5所示。混凝土桥墩采用实体单元C3D8R，钢筋采用桁架单元T3D2，二者通过相互作用模块中内置约束作用进行约束绑定。

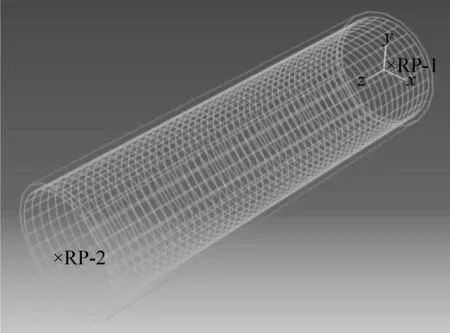
图5 实例桥墩有限元模型Fig.5 Example pier finite element model

3.2 材料参数的选取

混凝土参数选取实例桥墩采用的C30混凝土弹塑性参数见表1。实例C30普通混凝土桥墩本构关系采用C30混凝土塑性损伤本构模型，碳纳米管混凝土桥墩本构关系采用模拟验证得到的碳纳米管混凝土本构关系。钢筋选用实例桥墩采用的HRB400级，主筋直径为28 mm、螺旋箍筋直径为10 mm。钢筋本构模型采用双折线模型[17]。

图6 加载制度Fig.6 Loading system

3.3 定义分析步及加载制度

设置分析步定义模型的加载历程，具体步骤如下：

将模型底部完全固定的边界条件作为初始分析步，施加竖向荷载和水平反复荷载定位为step-1和step-2，分析步类型均为静力，通用。模型底部采用固定约束；顶部竖向施加集中荷载，大小为2.764 50×105N，横向采用位移加载，位移大小分别为0、1 、2、3 、4、6、 8、16、24、32、40、50、60 mm，每级循环一次，加载制度如图6所示。

4 碳纳米管混凝土桥墩抗震性能分析结果

4.1 滞回曲线分析

图7为普通混凝土桥墩与碳纳米管混凝土桥墩滞回曲线(PT为普通混凝土桥墩，CNT为碳纳米管混凝土桥墩)。由于未考虑钢筋与混凝土之间的相对滑移，滞回曲线没有出现捏拢效应。碳纳米管混凝土桥墩滞回曲线最后一个循环反向加载时，没有达到最大位移处，主要原因是由于网格划分精度不够，分析滞回曲线时，其影响可忽略不计。

从图7中可知：①相同循环荷载下，碳纳米管混凝土桥墩的承载能力、平均刚度都要大于普通混凝土桥墩，并且随着位移增大，两者逐渐接近达到同一水平。位移绝对值在0～0.04 m时，碳纳米管混凝土桥墩卸载时产生的塑性变形要略小于普通混凝土桥墩；位移绝对值在0.04～0.06 m时，碳纳米管混凝土桥墩卸载时产生的塑性变形要明显小于普通混凝土桥墩。②相同循环荷载下，当位移绝对值在0～0.04 m时，碳纳米管混凝土桥墩滞回环曲线包围的面积要大于普通混凝土桥墩；当位移绝对值在0.04～0.06 m时，碳纳米管混凝土桥墩滞回环曲线包围的面积要小于普通混凝土桥墩。这是由于本文提出的碳纳米管混凝土本构关系存在一定的误差，导致在位移过大时，表现出碳纳米管混凝土滞回环面积要小于普通混凝土桥墩的现象。

4.2 骨架曲线分析

图8为普通混凝土桥墩与碳纳米管混凝土桥墩骨架曲线(PT为普通混凝土桥墩，CNT为碳纳米管混凝土桥墩)。

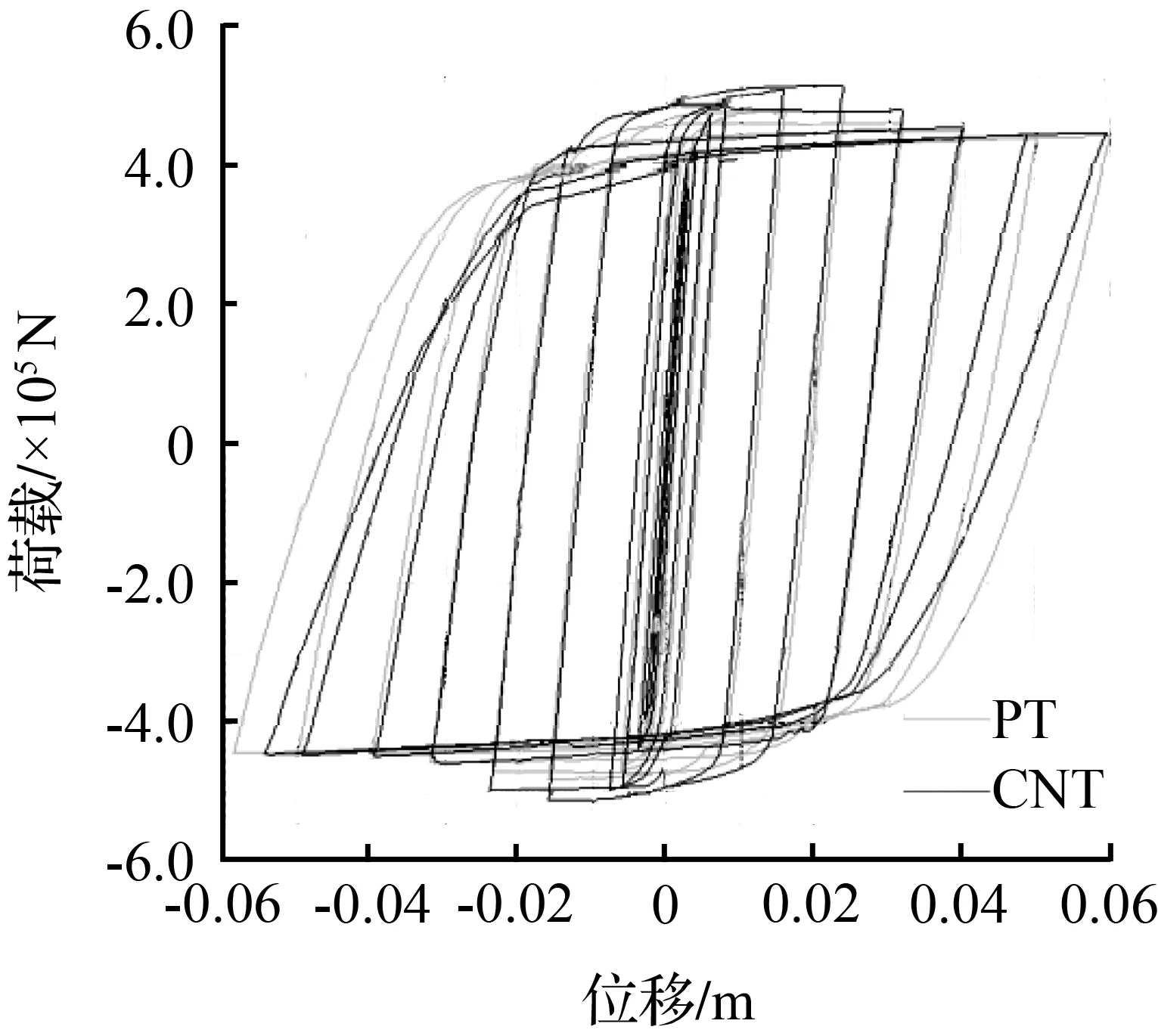
图7 滞回曲线比较Fig.7 Hysteresis curve comparison

图8 骨架曲线比较Fig.8 Skeleton curve comparison

从图8中可知：①弹性阶段内，两者曲线基本相同，位移较小，结构刚度比较大并且没有明显变化；屈服阶段内，随着位移的增加，结构的刚度急剧减小；破坏阶段内，碳纳米管混凝土桥墩下降较快，最后与普通混凝土处于同一水平保持不变。②碳纳米管混凝土桥墩的承载能力比普通混凝土桥墩高，并且极限承载能力相比于普通混凝土桥墩提高了7.3%，说明碳纳米管的掺入可以提升桥墩的承载能力。

4.3 位移延性系数

延性是指结构在进入屈服阶段直至破坏时的塑性变形能力。对于桥墩结构来说，一般采用位移延性系数μΔ来表示，可通过下列公式计算：

图9 骨架曲线极限位移确定Fig.9 Skeleton curve limit displacement determination

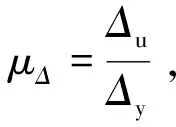
(9)

式中，Δu为桥墩墩顶的极限位移；Δy为桥墩的屈服位移。

上文已经得到了碳纳米管混凝土的骨架曲线，首先需要根据骨架曲线来确定桥墩的极限位移，如图9所示，根据文献[18-19]认为,当达到85%峰值荷载时桥墩达到破坏，破坏荷载所对应的位移即为极限位移。

本文通过能量等效法、作图法、R.Park法三种方法来计算碳纳米管混凝土桥墩的屈服位移并取其平均值，通过骨架曲线确定极限位移，最后计算出位移延性系数并与普通混凝土桥墩进行比较，计算过程与结果见表4。

从表4中可以看出，碳纳米管混凝土桥墩的位移延性系数相较于普通混凝土桥墩提升了11.5%，说明碳纳米管混凝土桥墩具有更好的延性。

表4 位移延性系数的计算结果Tab.4 Calculation result of displacement ductility coefficient

5 结论

本文主要利用ABAQUS有限元软件，建立了碳纳米管混凝土桥墩的有限元模型，分析了其在低周反复荷载作用下的抗震性能，并与普通混凝土桥墩进行比较，得到以下结论：

① 以分子动力学为基础，提出碳纳米管等效连续体模型和碳纳米管混凝土代表体积单元，通过模拟单轴受力试验拟合出碳纳米管混凝土本构关系公式，结合碳纳米管混凝土抗折试验，两者误差为4.1%，验证了公式的合理性。

② 碳纳米管混凝土桥墩的极限承载能力相比于普通混凝土桥墩提高了7.3%，且滞回环紧密饱满，表明其有良好的耗能性能。

③ 通过分析计算得到碳纳米管混凝土桥墩的位移延性系数为11.98，普通混凝土桥墩的位移延性系数为10.74，提升了11.5%，表明了碳纳米管混凝土桥墩具有更好的延性。