基于随机开裂理论的钢筋混凝土粘结损伤拉伸弹性性能

万里云彭聪张建常岩军123

(1.广西大学 土木建筑工程学院， 广西 南宁 530004；2.广西防灾减灾与工程安全重点实验室， 广西 南宁 530004；3.工程防灾与结构安全教育部重点实验室， 广西 南宁 530004)

0 引言

随着钢筋混凝土结构服役时间增加，其结构损伤和承载能力下降程度是结构安全服役评价的主要关注点，也一直是土木工程领域研究的热点之一。对于粘结损伤，一般的研究方法是通过大量拉拔试验拟合提出基于位置函数的粘结滑移本构模型[1]。当钢筋在复杂环境下产生锈蚀时，研究者也可以对不同锈蚀程度钢筋进行拔出试验，并基于试验数据分析锈蚀对钢筋混凝土粘结强度的影响，给出相应的粘结滑移本构关系[2]。而随着环保理念深入人心，新材料蓬勃发展，大量科研人员又开始了对于新型建筑材料粘结滑移性能的深入研究[3- 4]。这些以试验为基础的研究直观真实，但对于揭示更为细致深入的微观机理是有所不足。因此近年来，学者们开始从连续损伤理论、刚化效应等角度阐释钢筋混凝土的损伤本构关系[5]。

第一个试图去描述脆性基体复合材料应力应变关系的是AVESTON等[6-7]，并建立了ACK理论模型。然而ACK模型的主要的缺点是基体强度是一个确定的值[8-9]。针对脆性基体复合材料的应力应变关系，目前已经出现了一些类似的新理论，但由于其需要一些难以测量或获取的参数[10-11]，或会涉及一些复杂的断裂力学理论[12]，致使这些理论难以应用于实际情况。CUYPERS等[13]提出了基于Weibull随机开裂理论，用于研究E-glass(无碱玻璃纤维)增强IPC(无机磷酸盐水泥)材料。考虑随机开裂的ACK理论[6-7,14]能够用一些量化参数去模拟某种材料的应力应变行为，并且能够去预测脱粘段的摩擦剪应力。

考虑到实际钢筋混凝土性能损伤的复杂性，一则二者接触界面会同时存在脱粘段与粘结段，二则混凝土性能也具有随机分布特性。本文拟采用随机开裂的ACK理论建立钢筋混凝土单胞模型，探究在不同损伤阶段的单胞模型拉伸损伤等效弹性模量的变化规律。

1 ACK理论和随机开裂理论

1.1 ACK理论

ACK理论假设：

① 纤维仅承担轴向荷载，不考虑其抗弯，裂缝处轴向荷载全部由纤维承担；

② 在基体裂缝面附近，界面存在某一特定长度脱粘区域。脱粘界面剪应力τ0均匀分布;

③ 纤维与基体的泊松比影响不考虑；

④ 基体轴向正应力沿径向不变。

脱粘长度δ0可以通过基体受力平衡方程得到，可由下式计算：

(1)

式中，σm、Vm、Vf、r分别为基体内力、脱粘长度内基体体积、纤维体积和纤维半径。

WIDOM[15]通过理论推导，建立了脆性基体复合材料在轴向拉伸载荷作用下最终平均裂缝间距〈cs〉f与脱粘长度δ0的关系：

〈cs〉f=1.337δ0，

(2)

结合式(1)和式(2)，可计算出纤维和基体界面剪应力[10]：

(3)

ACK理论适合于脆性基体复合材料的损伤分析，其典型的的拉伸应力应变曲线根据非线性特征可以分成3段：第一段近似线性变化，该阶段基体开裂较少发生;第二段曲线的切线刚度不断下降，对应基体在多处开裂;第三阶段应力应变曲线切线刚度增大，出现硬化特征，对应基体裂纹数量增加减缓，裂纹密度趋于饱和。

1.2 随机开裂理论

由于受材料的制造工艺影响，基体的开裂应力具有一定分散性，需采用随机开裂理论，通过概率分布函数来描述其性能。裂缝能在多种应力水平下产生，当第一个裂缝产生时，纤维的桥联作用把裂缝两面连接起来，导致了在脱粘区域之外基体必须在更高应力水平下才能开裂，因此外部荷载能够继续增大。通过脆性基体材料试件三点弯试验[13]，发现两参数的Weibull分布适合用来描述脆性基体材料的拉伸强度随机性。在均匀拉伸荷载作用下，脆性基体失效概率的Weibull分布函数如下:

(4)

式中，P是失效概率;σCo是外加拉伸应力;σRe是参考应力;m是Weibull分布参数。

2 钢筋混凝土同心圆柱单胞模型随机开裂分析

混凝土是典型脆性基体，钢筋可类比为单纤维，由此建立基于考虑随机开裂的ACK理论的钢筋混凝土同心圆柱单胞模型(representative volume element, RVE)。随着外荷载的增大，混凝土裂缝依次产生并偏转到钢筋表面形成钢筋混凝土界面脱粘，裂缝面左右脱粘长度δ0为一定值，可由式(1)推导得到。钢筋混凝土单胞模型中钢筋和混凝土应力分布如图1所示，由图1(a)可知，当平均裂缝间距〈cs〉>2δ0时，混凝土应力曲线呈梯形状，应力峰值σcmax为一定值。由图1(b)可知，当〈cs〉<2δ0时，混凝土应力曲线呈三角形且应力峰值σcmax随着平均裂缝间距的不断减小而下降。基于上述分析，平均裂缝间距〈cs〉=2δ0，即为混凝土应力峰值变化与否的临界点，亦是反映裂缝宏观发展的程度的分界点。据此把钢筋混凝土单胞模型的损伤分成3个阶段，第一损伤阶段时混凝土材料内部无裂缝无脱粘，第二损伤阶段〈cs〉>2δ0，第三损伤阶段〈cs〉<2δ0。

基于随机开裂的ACK理论，当脆性开裂越充分直至稳定时，平均裂缝间距〈cs〉等于最终平均裂缝间距〈cs〉f。由式(2)和式(3)，钢筋混凝土单胞模型在某一轴向拉伸应力水平下的平均裂缝间距〈cs〉可由下式计算：

(5)

式中，σRVE为单胞模型总平均拉伸应力。

2.1 第一损伤阶段

此阶段中钢筋混凝土单胞中混凝土几乎没有开裂，钢筋和混凝土协同工作处于线弹性阶段。钢筋混凝土单胞模型的等效拉伸弹性模量为

ERVE=EsVs+EcVc，

(6)

式中，Es，Ec分别是钢筋和混凝土的弹量；Vs，Vc为二者体积分数。

此时在钢筋混凝土同心圆柱单胞模型中，钢筋和混凝土的轴向应力和轴向应变分别为σs，σc和εs，εc，单胞模型总应变εRVE。远场应力σs为σs0，应变εs0=εc0=ε0。

所以有

(7)

单胞平均应力σRVE即为

σRVE=σs0Vs+σc0Vc=(EsVs+EcVc)εs0。

(8)

2.2 第二损伤阶段

图1所示为在钢筋混凝土单胞模型中脱粘范围内混凝土和钢筋的应力变化情况。当混凝土裂缝产生并扩展到钢筋表面时，在裂缝处的钢筋承担所有轴向荷载，此处钢筋内力为最大值σsmax，混凝土内力为0。ACK理论中摩擦剪应力τ0规定均匀分布，因此钢筋和混凝土应力的变化形式在δ0内为线性。从原点位置起沿脱粘界面，钢筋受到混凝土传来的均匀不变的剪力τ0，应力线性减小。同时，混凝土内力也在τ0作用下线性升高。而二者的内力，在超出脱粘范围后保持恒定。

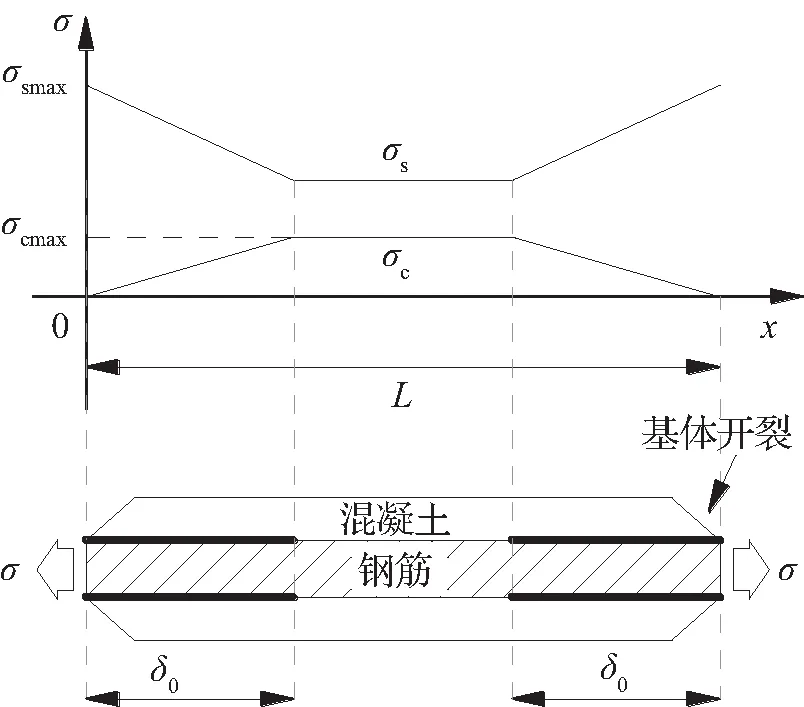
(a) 第二损伤阶段：〈cs〉>2δ0

(b) 第三损伤阶段：〈cs〉<2δ0

基于图1(a)中钢筋的应力变化曲线及胡克定律，用面积积分求值的方法计算钢筋的伸长量。为方便表达，令L=〈cs〉，钢筋的伸长量ΔL计算如下：

(9)

式中，混凝土开裂处钢筋内力σsmax为

(10)

把式(10)代入式(9)化简得

(11)

所以单胞模型的轴向平均应变为

(12)

在第二损伤阶段，单胞模型的等效弹性模量：

(13)

2.3 第三损伤阶段

当加载于单胞模型两端的轴向力逐渐增大，混凝土产生和延展了更多裂缝。此时裂缝开展逐渐充分，钢筋混凝土单胞模型进入第三损伤阶段，满足平均裂缝间距〈cs〉<2δ0，因推得钢筋和混凝土应力在脱粘段为线性变化，基于图1(b)中钢筋的应力变化曲线及胡克定律，用面积积分求值的方法计算钢筋的伸长量。为方便表达，令L=〈cs〉，钢筋的伸长量ΔL计算如下：

(14)

此时，混凝土开裂处钢筋内力σsmax为

(15)

把式(15)代入式(14)化简得

(16)

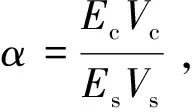
(17)

在第三损伤阶段，单胞模型的等效弹性模量：

(18)

3 参数影响分析

本节主要探究钢筋混凝土单胞模型中的钢筋和混凝土体积分数Vs、Vc，Weibull分布参数m，混凝土强度等级等参数对等效拉伸弹性模量的影响。基于上节内容，易建立等效弹性模量E与单胞拉伸应力σRVE之间的函数关系。图2描述了参数取值分别为Es=2×105MPa，Ec=3×104MPa，Vs=0.1， Vc=0.9，ftk=2.01 MPa，m=2时，等效弹性模量随单胞拉伸应力σRVE的变化过程，曲线分成3段，分别对应粘结损伤单胞分析模型的3个阶段。在第一损伤阶段钢筋和混凝土共同变形，无裂缝无脱粘，等效弹性模量为一定值。随着混凝土裂缝的产生与发展，模型内部脱粘损伤增多，等效模量在第二损伤阶段大幅下降。在第三损伤阶段，裂缝发育较完全，混凝土基本丧失持荷能力，因此等效模量趋于平稳。

3.1 钢筋和混凝土体积分数对等效模量E的影响

在图3中，3条曲线对应不同情况下的混凝土和钢筋体积分数，图3中虚线表示3条曲线具有相同的临界应力，该临界应力是第二、第三损伤阶段的分界。因〈cs〉=2δ0时，σRVE只与混凝土抗拉强度ftk，Weibull分布参数m有关。从曲线的间隔看，3条曲线的间隔较为均匀，这反映了两种材料体积取值的梯度性

3.2 Weibull分布参数m对等效模量E的影响

在图4中，随着Weibull分布参数m的变化，等效弹性模量E随σRVE的变化过程有了显著不同。m值存在于混凝土断裂强度分布状态函数中，由混凝土拉伸强度的分散性决定。从m=2变化到m=8的过程中，3条曲线在第二损伤阶段下降过程由缓变陡。这说明Weibull分布参数m对曲线下降的速率有影响，m的值越大，曲线下降越快，且越早达到稳定状态。图4中虚线代表了3条曲线的分段点处的等效模量相等，此时3条曲线对应的σRVE都满足〈cs〉=2δ0。

3.3 混凝土强度等级对等效模量E的影响

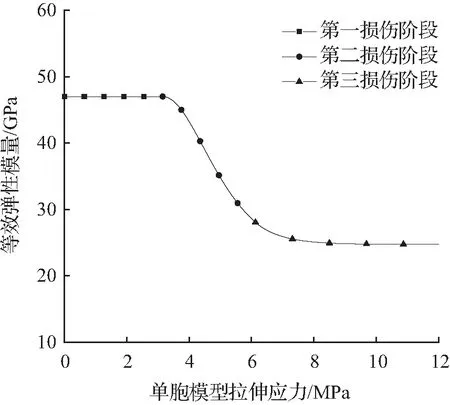
图2 等效弹性模量E随单胞拉应力σRVE变化曲线Fig.2 Equivalent elastic modulus E curve with the tensile stress of model

图3 不同体积分数下的等效弹性模量E变化曲线Fig.3 The curves of equivalent elastic modulus E for different values of volume fraction

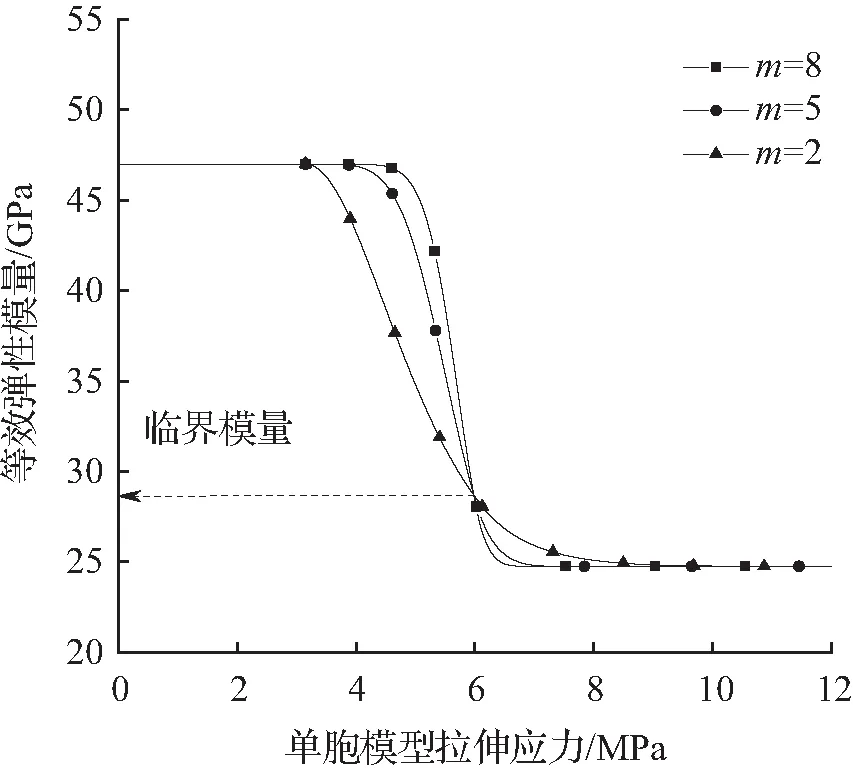
图4 不同m下的等效弹性模量E变化曲线Fig.4 Curves of equivalent elastic modulus E for different values of m

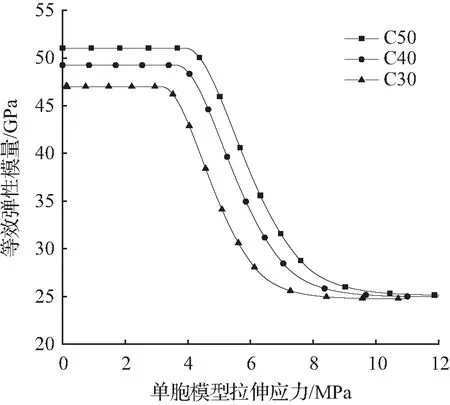
图5 不同混凝土强度等级的等效弹性模量E变化曲线Fig.5 Curves of equivalent elastic modulus E for different values of concrete strength

4 结论

本文基于随机开裂的ACK理论，建立了钢筋混凝土拉伸损伤单胞分析模型，推导出不同损伤状态下的等效弹性性能，得到如下结论：

① 第一损伤阶段钢筋混凝土材料处于线弹性范围，内部无裂纹无损伤，等效模量不变。第二损伤阶段混凝土裂缝密度逐渐增大，单胞承载力逐渐减弱，因此等效模量逐步减小。第三损伤阶段混凝土开裂趋于饱和，基本丧失承载能力，因此等效模量值主要受钢筋影响，并接近EsVs。

② 混凝土抗拉强度的分散性决定了其断裂强度的分布函数中m值的大小。m值越大，第二损伤阶段发生的应力区段宽度越小，曲线下降越急剧。

③ 混凝土强度等级越高，对应的弹性模量Ec越大，因此在拉伸损伤单胞模型的初始等效弹性模量的值越大。在第三损伤阶段，混凝土因开裂损伤严重，承载力贡献越来越小，此时等效弹性模量主要受钢筋模量和体积分数影响。

④ 随着钢筋混凝土单胞模型中钢筋体积分数Vs的增加，其等效弹性模量曲线整体升高。Vs的值取决于钢筋周围混凝土横向裂纹的扩展范围，其合理的取值还需进一步研究。