考虑轮载冲刷的水泥混凝土路面模型尺寸确定

224

(1.重庆交通大学 土木工程学院， 重庆 400074；2.重庆交通大学 交通土建工程材料国家地方联合工程实验室， 重庆 400074；3.中铁二院 重庆勘察设计研究院有限责任公司， 重庆 400023；4.重庆交通大学 山区桥梁结构与材料教育部工程研究中心， 重庆 400074)

0 引言

水泥混凝土路面板底接缝处的基层由于存在滞留水，在行车荷载作用下会产生严重的局部冲刷现象导致脱空、错台等病害[1]。因此有必要掌握水泥混凝土路面接缝处基层的冲刷过程及破坏情况。

目前国内多采用MTS冲刷试验设备模拟动水压力对基层试件来开展抗冲刷试验，但是此方法未实现存在面板参与的冲刷过程且难以考虑接缝对基层冲刷的影响。有研究人员采用车辙试验设备开展具有面层或覆盖层的基层轮载抗冲刷试验，其加载方式是循环往复式，与实际单向荷载作用存在差异，这与板底接缝处基层冲刷状况差异较大，因此考虑采用MMLS3加速加载设备开展冲刷试验，以期模拟较为真实的冲刷状况。

现有轮载加载冲刷试验中，JUNG等[2]使用汉堡车轮跟踪装置测试基层的抗冲刷性，圆柱形试件由25.4 mm(1 in)的面层、25.4 mm(1 in)的基层和9.5 mm(3/8 in)的底基层组成，其平面直径为153 mm(6 in)。高伟等[3]采用车辙试验机进行轮碾冲刷试验，试件尺寸为300 mm×300 mm×47 mm车辙板尺寸。目前，试件的形状和尺寸尚不统一并且无统一的选尺依据，现有研究较少有考虑缩尺和局部情况对冲刷的影响。党彦[4]分析道路面板不同尺寸试件的尺寸效应对应力、应变的影响，张颖[5]基于混凝土尺寸效应开展细观数值模拟、分析细观尺寸效应，李淑明等[6]基于MMLS3设备对沥青路面结构的尺寸开展研究，结果表明试件尺寸对试验结果有较大影响。苏志翔等[7]开展针对沥青路面结构的MMLS3室内加速加载试验模型的相似性设计。但鲜有研究针对水泥混凝土面板、半刚性基层开展研究，难以确定水泥混凝土路面半刚性基层冲刷试验合理尺寸。基于MMLS3设备开展水泥混凝土路面板底接缝处基层冲刷研究，需采用合理的试件尺寸，才能得到与实际较符的冲刷规律。

本文基于MMLS3加速加载设备试验条件，应用有限元方法建立足尺路面结构模型，基于相似理论和尺寸效应对局部缩尺模型进行合理尺寸设计，并采用拟合手段对足尺模型和局部缩尺模型开展相似性分析，分析足尺模型和局部缩尺模型相似性，为室内试验进一步开展提供依据。

1 模型分析思路及相似理论分析

1.1 模型分析思路

分析思路主要分为4个阶段：

阶段一：依据水泥稳定碎石基层水泥混凝土路面典型结构，基于圣维南原理和弹性半空间地基假设，选定面层、基层和土基的合适尺寸，采用计算结果趋于收敛的最优网格精度，建立足尺模型，验证模型正确性。

阶段二：结合足尺模型计算结果，以板底压应力为评价指标，考虑不同试件尺寸产生的应力应变响应，选取足尺模型面板横向接缝处的应力集中区域作为局部范围合理的尺寸，初步建立局部模型。

阶段三：在初步局部模型基础上，考虑加速加载条件，基于相似理论和弹性薄板小挠度理论，初步建立局部缩尺模型。

阶段四：以板底压应力作为分析指标，分析足尺模型和局部缩尺模型的计算结果的相关性，建立二者相似对应关系，从而确定模型合理尺寸。

1.2 相似理论基本原理

相似原理的理论基础由3个核心定理组成[8]。

① 相似第一定理(相似正定理)：相似系统(相似现象)的相似指标等于1或相似判据(相似准则)相等[8]。以相似第一定理作为指导，通过推导相似条件，并获取模型所需的物理量，通过相似推断原模型。

② 相似第二定理(π定理)：一个物理系统，若含有n个物理量，其中有k个物理量的量纲是相互独立的，则这n个物理量可表示成n-k个独立的相似准则π1,π2,…,πn-k之间的函数关系即y(π1,π2,…,πn-k)=0[8]。通过相似第二定理找出研究现象的物理规律性，规律性通常以物理量之间的函数关系表现出，各量纲的物理量取决于其的单位制。

③ 相似第三定理：对于同一类物理现象，即由文字结构相同的方程(组)所描述的物理现象，如果单值条件相似，而且由单值条件的物理量所组成的相似判据在数值上相等，则现象相似[8]。相似第三定理将具体现象与单值条件相联系，强调单值量相似，考虑到单值量的变化特征。

针对试验模型进行相似性分析，步骤如下：首先确定物理量和基础物理量进行量纲分析，依据量纲矩阵和量纲和谐原理得出相似准则，其次根据Buckingham π定理确定模型的相似指数，依据相似确定试件尺寸，最后建立经验公式。

1.3 相似分析

本文以水泥稳定碎石基层水泥混凝土路面结构为研究对象，确定各物理量的相似指标开展相似理论分析。

MMLS3加速加载条件的荷载属于动态荷载，因此在模型路面结构中采用子程序载入移动均布荷载的方式加以实现。

首先，将路面结构简化为3层结构，分别为面层、基层和土基。采用弹性层状体系作为力学分析基础理论，以双圆垂直均布荷载作用下的结构层的层底拉应力作为设计指标[9]，因此选取面层层底的拉应力、拉应变和路面整体弯沉作为相似模型设计的力学控制指标[7]。通过对该模型进行分析，表征该路面结构的物理量：结构层平面尺寸、接缝尺寸及车轮尺寸X；面层和基层的各参数，其中模量E1、E2，泊松比μ1、μ2，密度ρ1、ρ2，厚度h1、h2；荷载应力σ、应变ε；位移δ；轮载压力P。各主要物理量的量纲见表1，以质量M、长度L和时间T的单位作为基本量纲，将各物理量的单位转化为基本量纲的单位形式。

表1 各物理量的基本量纲Tab.1 Dimensions of each physical quantity

假定相似准则如下：

(1)

整个系统有13个物理量，组成量纲矩阵见表2。其中假定用a，b，c，…，l，m分别代表X，E1，E2，μ1，μ2，ρ1，ρ2，h1，h2，σ，ε，δ，P的指数。

表2 系统物理量的量纲矩阵Tab.2 Dimension matrix of system physical quantities

由上述量纲矩阵得出物理量间关系的联立方程：

b+c+f+g+j+m=0，

(2)

a-b-c-3f-3g+h+i-j+l+m=0，

(3)

-2b-2c-2j-2m=0。

(4)

表征水泥路面结构的物理量共13个，基本量纲有3个，根据Buckinghamπ定理，相似准则的个数为10个。3个方程无法求13个未知量，假设a，b，f是未知量，将其余未知量用表示：

a=-h-i-l-2m，

(5)

b=-c-j-m，

(6)

f=-g。

(7)

对上式进行线性变换，相应的π矩阵见表3。

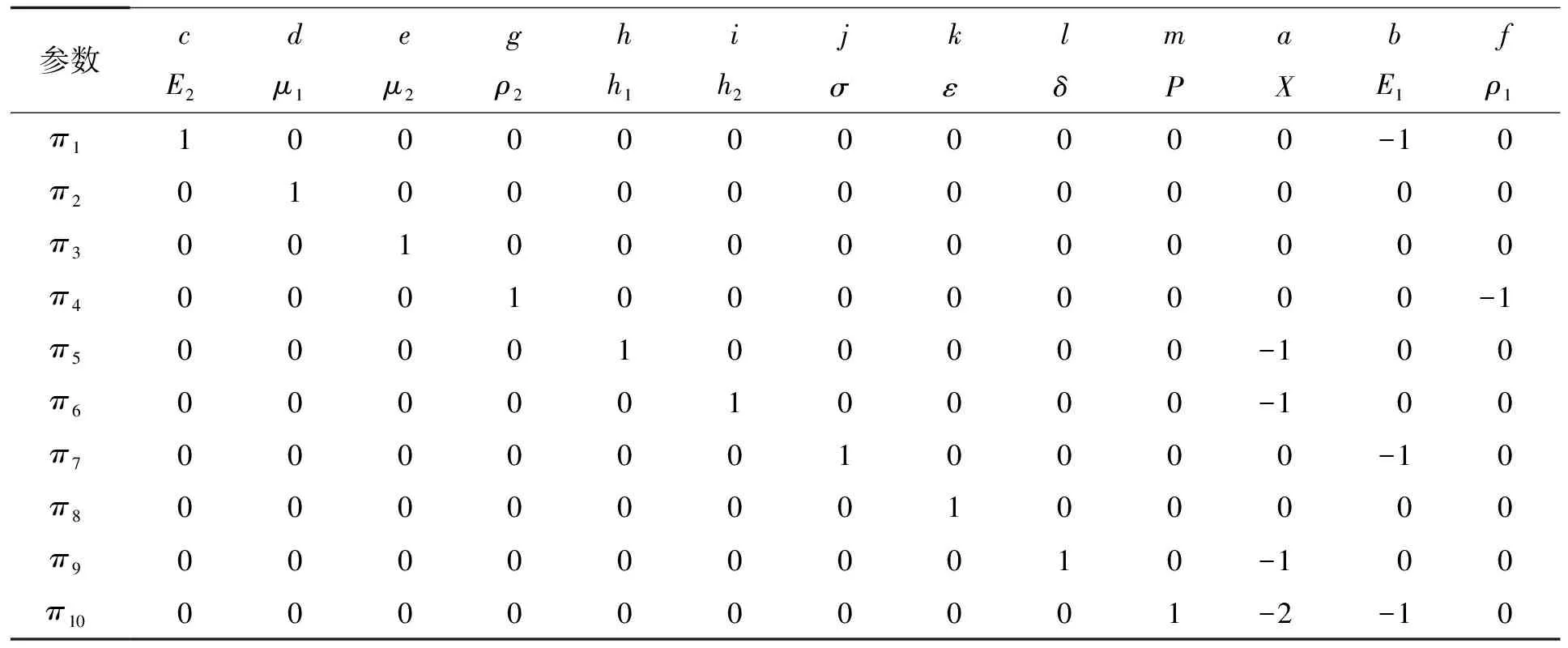
表3 π矩阵Tab.3 π matrix

由量纲矩阵和量纲和谐原理解得10个相似准则：π1=E2/E1，π2=μ1，π3=μ2，π4=ρ2/ρ1，π5=h1/X，π6=h2/X，π7=σ/E1，π8=ε，π9=δ/X，π10=P/X2E1。

根据相似定理的Buckingham π定理，由于现象相似对应的同名准则数值相同，可确定各参量的相似常数。可确定水泥路面模型的相似常数如下：

足尺路面和模型路面材料选取一致，面层材料的各参数的相似常数为CE1=Cμ1=Cρ1=1，可得出基层材料各参数的相似常数为CE2=Cμ2=Cρ2=1。

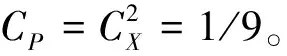
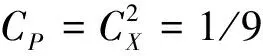
由以上可得出各系统物理量的相似常数，见表4。

表4 系统物理量的相似常数Tab.4 Similar constants of system physical quantities

2 足尺模型构建

实际路面结构在平面尺寸上属于无限体[6]，参考水泥混凝土路面典型结构，确定模型结构各层的材料和尺寸参数。为模拟行车荷载在路面上的实际情况，模型采用移动荷载模拟轮载条件。冲刷过程中基层顶面由于面板压力对水施加压力产生基层冲刷现象，因此以板底压应力作为分析指标分析模型应力应变响应，并探究网格精度对该模型数据的影响以求找出最优网格精度，并验证其正确性。

2.1 尺寸选定及依据

根据圣维南原理，采用有限元方法确定土基不受边界尺寸效应影响的合理尺寸，初步确定平面尺寸建立多组不同基层厚度模型，计算出合理地基尺寸为15.00 m×7.00 m×6.00 m。假定半刚性基层平面尺寸与地基一致，厚度取0.18 m。水泥混凝土路面典型平面尺寸为5.00 m×4.00 m，厚度取0.22 m。面层设有宽度为0.01 m的横向接缝[11]，此接缝形式是缩缝并考虑行车荷载和温度应力作用下贯穿，因此简化为贯穿缝。各结构层尺寸见表5。

表5 结构层尺寸Tab.5 Structural layer size

2.2 相关参数选定

2.2.1 材料参数

本文选取的各层材料参数[12]见表6，假定路面结构各层材料均为线弹性材料。

表6 材料参数Tab.6 Material parameters

2.2.2 边界条件和层间接触条件

假定面板四周无约束为自由边，基层和土基约束其法向位移，土基底面固定，各结构层层间接触条件、填缝料和面板的接触条件设为完全连续，即接触面完全接触[6,12]。

2.2.3 荷载条件

采用MMLS3加速加载仪的加载条件模拟移动荷载情况，假定车辆轮载为垂直均布矩形荷载，加载轮组为单轴单轮组，采用单次移动荷载形式，试验过程模拟轮胎单方向沿荷载移动带行驶两块面板并经过面板横向横缝。轮载加载速度为2.5 m/s，即9 km/h，接地压力为0.7 MPa，接地荷载面积为0.227 7 m×0.156 8 m[13]，即0.035 7 m2。

2.3 网格划分方法及影响

网格划分的精度对有限元计算结果存在影响，过粗网格会导致应力分布不均、变形量大，随着网格细化，单元精度提高，应力应变分布光滑，有限元解趋于收敛趋近于精确解，但是计算量随单元增多骤增。因此应合适的网格精度以满足计算的需要，实现精度与效率的最优组合[14]。为了找出最优网格，本文开展了多网格划分方法研究。

在路面结构设计中，以板底弯拉应力为设计指标，但本模型为模拟基层冲刷情况，在冲刷过程中动水压力由面板产生挤压与泵吸作用对基层产生冲刷，水压力主要受到板底压应力的影响，所以本文选取板底压应力为分析指标研究模型应力应变响应。以车轮行驶方向作为纵向，垂直于行驶方向为横向，对模型分析纵向中轴线的应力和横向中轴线的应力。

有限元模型单元选用C3D8R单元，足尺有限元模型网格初步考虑以轮载面积为初始网格，如图1所示。水平网格选用正方形以荷载面积长边作为选尺，面板横线接缝处以该处尺寸划分网格；竖向网格以各层尺寸为基础，面层划分两层，基层划分一层，土基处由上之下的网格划分为由密至疏，初始网格1模型。图2为面板俯视视角的网格划分情况，单元数及节点数均为整体模型的值。

图1 足尺模型(初始网格1)Fig.1 Full scale model (initial grid 1)

图2 初始网格1(单元数33 802，节点数40 272)Fig.2 Initial grid 1 (unit 33 802, nodes 40 272)

结合图3对初始网格1模型进行计算分析，以板底压应力为指标，分析应力集中的范围，初步分析得出纵向应力集中范围为683.1 mm，横向应力集中范围为627.2 mm，得出应力集中区域为683.1 mm×627.2 mm。

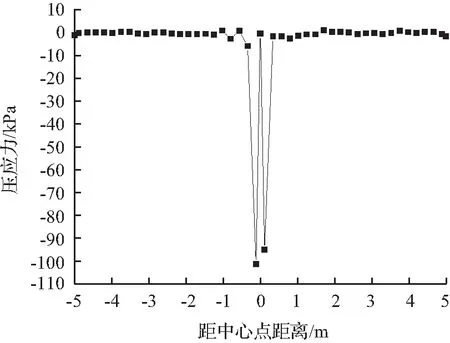
(a) 纵向

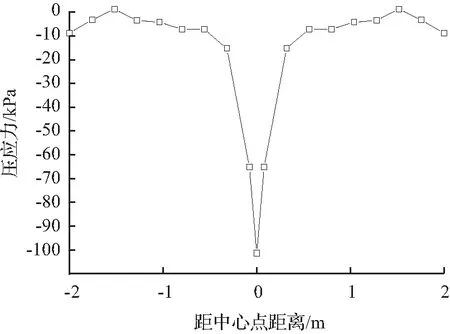
(b) 横向

以单个荷载面积为基准对初始网格1模型应力集中范围进行网格细化，得局部细化网格2模型，如图4所示。因竖向尺寸偏小不一划分过细，因此现网格细化仅针对水平面，暂不考虑竖向。以单个荷载面积为基准对网格全局细化得到整体细化网格3模型，如图5所示。

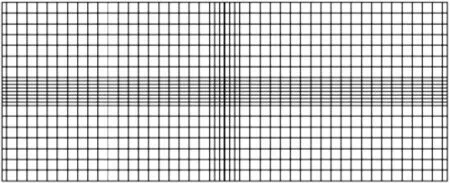
图4 局部细化网格2(单元数45 438，节点数53 568)Fig.4 Local refinement grid 2 (unit 45 438, nodes 53 568)

图5 整体细化网格3(单元数139 368，节点数162 048)Fig.5 Overall refinement grid 3 (unit 139 368, nodes 162 048)

因路面结构设计中面板以受弯拉为主，为验证网格细化的可行性，以纵方向应力作为考虑标准。结合图6的局部细化网格2模型与初始网格1模型的计算结果，对面板板底纵向应力进行对比分析，将应力集中区域细化网格与细化前网格对比，可得主应力影响可以忽略，因此该细化方案可行。

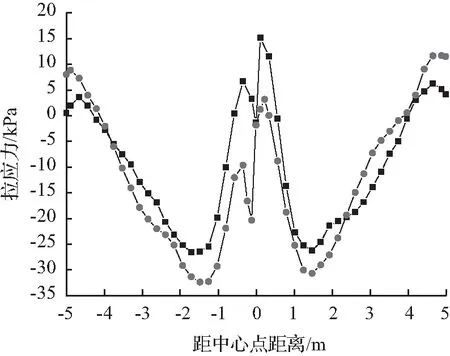
(a) 拉应力

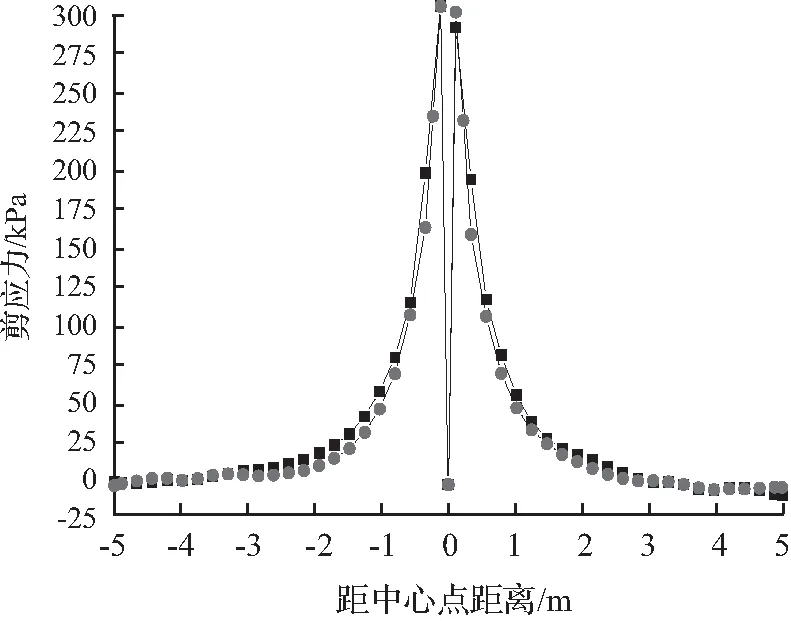
(b) 剪应力

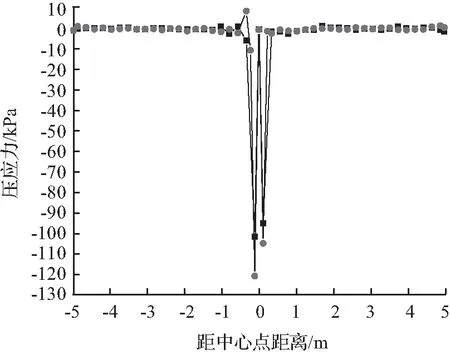
(c) 压应力

以板底压应力为指标，结合图7对网格2与网格3的面板纵向和横向的应力进行分析，可得出结论：网格的全局细化与局部细化结果变化不大，影响可忽略不计。确定采用局部细化网格2模型，对局部非荷载区域进行网格细化，以面板板底竖向主应力为指标进一步确定应力集中范围。

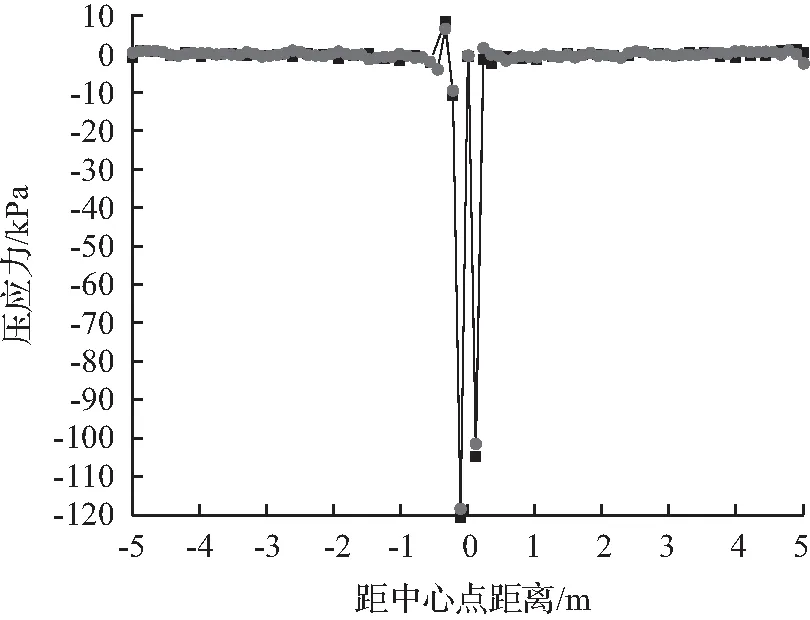
(a) 纵向

图7 网格2与网格3的压应力Fig.7 Compressive stress of grid 2 and grid 3

有限元计算结果随网格的细化逐渐收敛。因此对局部细化网格2模型进行多次细化，对应力集中区域分2次细化，分别为局部细化网格4模型、局部细化网格5模型。局部细化网格4模型，对网格2模型的纵向(车轮荷载行驶方向)局部范围内网格进行一次细化即加密该处网格为原网格两倍，如图8所示；局部细化网格5模型，对网格2模型的纵向(车轮荷载行驶方向)和横向(垂直于车轮荷载行驶方向)局部范围内对网格各一次细化即加密该处网格为原网格四倍，如图9所示。

图8 局部细化网格4(单元数49 578，节点数58 392)Fig.8 Local refinement grid 4 (unit 49 578, nodes 58 392)

图9 局部细化网格5(单元数63 270，节点数74 208)Fig.9 Local refinement grid 5 (unit 63 270, nodes 74 208)

结合图10对局部细化网格4、5模型计算，以板底压应力为指标，将网格4、5与网格2模型进行对比分析，随着网格逐步细化纵向和横向压应力随荷载区域网格细化增大并趋于收敛，且随细化程度加深可使面板板底压应力过度平滑。

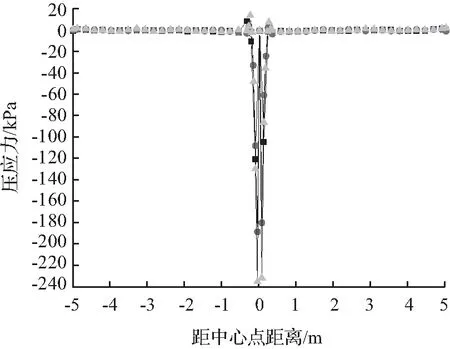
(a) 纵向

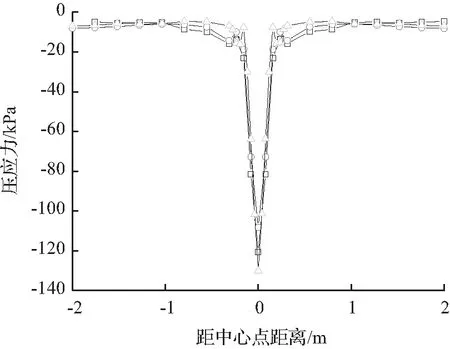
(b) 横向

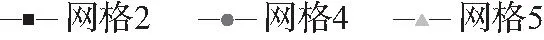
图10 网格2、4、5的压应力Fig.10 Compressive stress of grids 2, 4, 5

至此该模型网格划分经历5种划分情况，即初始网格1、局部细化网格2、整体细化网格3、局部细化网格4、局部细化网格5。由上述5种网格划分分析结果，足尺模型网格划分选用局部细化网格5划分方式。

2.4 模型验证

本文考虑在行车荷载下水泥混凝土面板的受力情况，采用有限元软件分析荷载位于板中时的最优网格单板足尺模型，以板底最大拉应力为分析指标，将有限元计算结果与修正后的Westergaard计算公式[15]的结果进行对比，结果见表7。由表7可以看出，有限元计算结果与Westergaard理论解较为接近。由于本文建立模型为平面双板结构，所以采用接缝传荷系数验证接缝传荷能力。现有研究结果表明，在不设传力杆的情况下接缝传荷系数在30%～70%范围内[16]，此模型计算所得接缝传荷系数为65.76%满足要求。这说明本文所建模型较为合理。

表7 板底最大拉应力Tab.7 Maximum tensile stress at the bottom of the plate

3 局部缩尺模型构建

在室内试验中由于试件存在尺寸限制的问题，须确定室内试验试件的合理尺寸。考虑采用有限元法分析出各结构层的合理尺寸，以满足室内试验要求。基于水泥混凝土双板结构足尺模型分析数据，以板底压应力为分析指标，选取模型横向接缝处应力集中区域作为局部范围，构建足尺模型的局部模型，结合相似理论进一步建立局部缩尺模型。

3.1 缩尺模型尺寸确定

3.1.1 局部模型尺寸

为研究在MMLS3加速加载作用下基层冲刷试验中路面结构试件的尺寸，建立有限元模型。因为MMLS3加速加载仪是1/3缩尺模拟轮载加载条件，考虑相似缩尺条件下研究应力集中区域的局部应力应变响应。而在行车荷载作用下，基层冲刷是由饱水基层中的自由水在面板挤压下形成高压水流产生了冲刷，在冲刷过程中面层板底压应力起主导作用，所以本文选取板底压应力作为横向接缝处应力集中区域的评价指标。

有限元模型单元选用C3D8R单元，并基于最优网格(即局部细化网格5)建立水泥混凝土双板结构足尺模型，分析纵向(车轮行驶方向)和横向(垂直车轮行驶方向)两个方向计算结果，重点研究荷载位于接缝时刻的横向接缝处板底压应力。

结合图11分析，考虑压应力主要影响范围选取应力集中区域，在纵向选取曲线突变点作为应力突变点，由此得出应力集中范围约为0.427 m；横向选取曲线突变点作为应力突变点，可得出应力集中范围约为0.291 m。

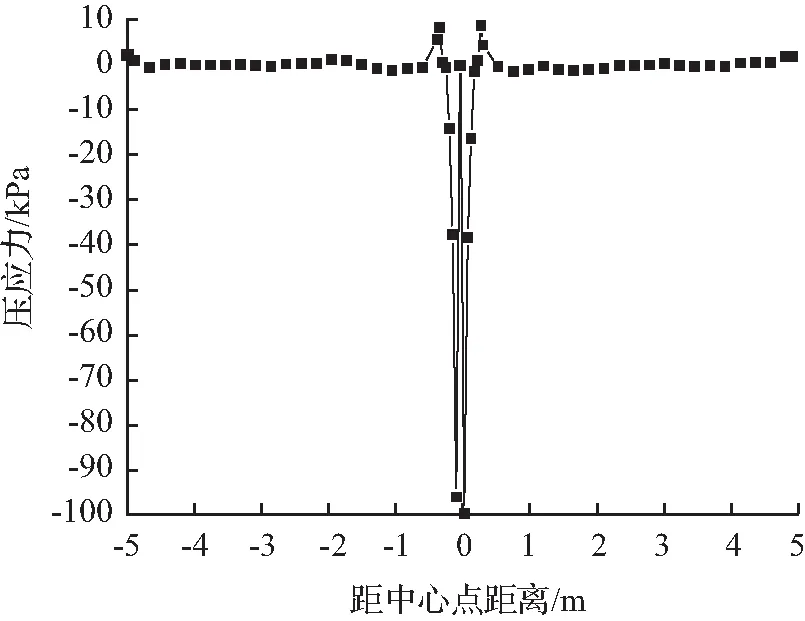
(a) 纵向

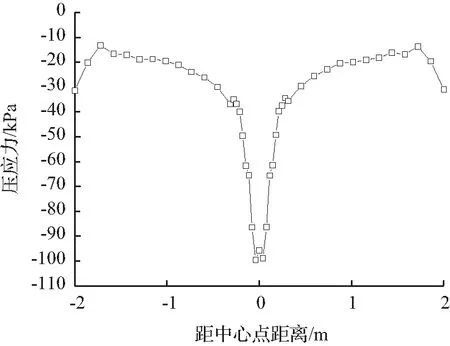
(b) 横向

由两个方向上的应力集中范围作为选尺依据，确定局部模型平面尺寸为0.45 m×0.30 m。该局部区域横跨接缝，因此接缝宽度仍为0.01 m。基层厚度为足尺模型厚度0.18 m，面层厚度为依据足尺模型厚度0.22 m，但面层厚度应满足弹性薄板小挠度理论，即厚度尺寸h小于平面尺寸最短边b的1/5，因此面层厚度选取为0.06 m。针对局部缩尺模型而言，路基成型与缩尺均较为困难，且可能由于路基压实不足等原因导致路面病害产生，影响冲刷试验效果，所以在缩尺模型设计时，不考虑路基，仅设置基层与面层结构。

3.1.2 局部缩尺模型尺寸

基于相似分析结论中所得路面结构的相似参数1∶3对局部模型进行相似缩尺，得出局部模型各结构层的各尺寸，其中接缝宽3.3 mm，面板尺寸为单板尺寸，其余尺寸见表8。

表8 各结构层尺寸Tab.8 Size of each structural layer

3.2 相关参数选定

3.2.1 边界条件和层间接触条件

该模型假定面板和基层约束模拟实际试验情况，即四周约束其法向位移(约束四个自由度)，基层底面固定，各层间接触条件及填缝料和面板的接触条件设为完全连续。

3.2.2 荷载条件

模拟MMLS3加速加载仪的加载条件，轮载为单轴单轮组采用单次移动荷载形式，模拟轮胎单方向驶经面板横向横缝，加载速度为2.5 m/s即9 km/h，轮载接地压力为0.7 MPa，轮胎接地面积为8 cm×5.2 cm[17]，即41.6 cm2，试验轮接地尺寸约为原型的1/3。

3.3 网格划分

该局部缩尺模型的网格划分选用局部细化网格5划分方式进行划分。

4 模型相似性分析

4.1 相关分析

相关系数是用以反映随机变量或者观测数据值之间关系亲密程度的统计指标，表明变量之间的相关性和依赖性，用于两个或者多个随机变量之间的相似性分析[18]。在统计学中，Spearman相关系数是一种衡量两个变量之间依赖性的非参数统计指标，可以进行两个变量独立性的非参数检验[19]。该两模型的数据符合此特点，因此本文采用Spearman相关系数对局部模型和局部缩尺模型进行相关分析。

采用统计分析软件对模型路面和原型路面有限元模型各项参数进行Spearman相关性分析，以评估局部模型和局部缩尺模型的相似性，模型参数见表9。该两个模型计算可得的Spearman相关系数为0.695，在0.05的水平上相关性显著。因此，局部模型和局部缩尺模型具有较高的相似性。

表9 局部模型和局部缩尺模型有限元模型参数Tab.9 Local model and local scale model finite element model parameters

4.2 荷载应力相似性分析

通过对足尺模型和局部缩尺模型计算结果开展分析，选择车轮荷载位于横向接缝处时刻，对纵向轮迹带下的板底压应力进行相似性分析。由图12可知，将局部缩尺模型纵向压应力乘以相似系数转化为局部模型的相似应力值，对足尺模型与局部缩尺模型的压应力进行分析，在一致的车轮荷载下应力变化趋势相似，位于接缝处点应力一致，由接缝向板边延伸方向的应力变化趋势一致即先增大后减小，靠近接缝处的点应力为最大值，该点至板边应力值逐渐减小。局部缩尺模型板边的点与足尺模型有差异，因模型无法完全模拟局部处边界条件因此考虑忽略局部缩尺模型边界处点的应力情况。

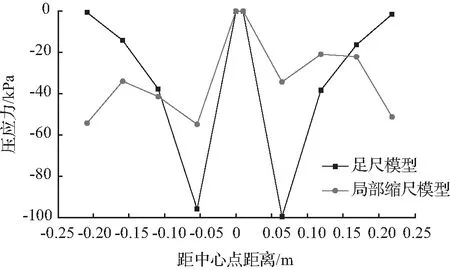
图12 两模型纵向压应力Fig.12 Longitudinal compressive stress of the two models

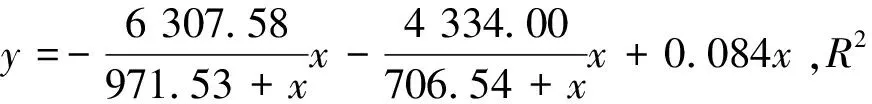
5 结论

本文在结合MMLS3加速加载仪的实验条件下通过建立双面板的水泥混凝土路面结构足尺模型和局部缩尺模型，研究了轮载冲刷试验中试件的合理尺寸以及模型相似关系，主要结论如下：

① 通过建立的双板路面结构试件足尺模型并进行分析计算，以板底竖直压应力作为评价指标选取应力集中范围初步确定局部区域，并依据相似理论，确定了初步的局部缩尺模型尺寸。

② 对足尺模型和局部缩尺模型开展了相关分析和相似性分析，结果表明所建立的局部缩尺模型可有效地模拟在行车荷载下实际路面的受力情况，两模型具有较高的相似性，从而确定局部缩尺模型的合理尺寸，其中模型平面尺寸0.15 m×0.10 m，竖向尺寸分为面层0.02 m和基层0.06 m，面层的接缝宽3.30 mm。

③ 开展足尺模型多网格精度分析，基于应力收敛的依据确定模型最优网格，可为后续不同模型的网格划分的合理性和最优性提供依据。

④ 本文提出的结构模型的尺寸确定方法及研究思路可为相关加速加载试验设计提供参考。