基于S-Catboost算法的短时公交客流预测及影响因子分析

夏弋松，靳文舟

(华南理工大学 土木与交通学院， 广东 广州 510641)

0 引言

影响城市公交客流预测的因素十分复杂，传统的公交客流预测主要从纯数理统计的角度对公交客流进行拟合。多运用时间序列、自回归模型、灰色系统等统计方法进行预测。然而，公交客流随时间波动趋势明显，受天气、节假日、乘客类型等诸多因素影响。传统的统计科学预测方法很难对客流变化的本质规律和影响机理做出解释，模型对不同数据的适应性也比较差，预测精度亦不尽如人意。

近年来，随着人工智能领域和机器学习各类算法的蓬勃发展，诞生了很多新的数据预测方法。比如神经网络模型、SVM支持向量机、随机森林以及各类决策树模型。这些方法和模型的预测精度和准确性较传统方法要好，在电商、电力等领域已经有了较为成熟的应用场景，国内外也有少部分的学者将这类新型预测方法用于交通领域，但是相关的文献还比较少，研究进展不够深入。

鉴于这种情况，为了充分发挥公共交通领域大数据的价值，对公交短期客流作更精准的预测，本文采用梯度提升决策树模型对多元公交客流数据进行短期预测，以期找到精准度和泛化性更强的机器学习模型，提升S-Catboost模型对不同类型短期客流预测的适应性，让机器学习在公共交通领域获得更多应用场景。

如何建立一个能够精准、有效地预测短时公交客流的客流预测模型一直是公共交通领域十分热门的问题，在机器学习和深度学习相关的算法理论问世之前，大部分学者使用的都是传统的统计学预测模型，例如传统的线性及非参数回归模型[1-2]、逻辑回归模型以及ARIMA[3- 6]自回归移动平均时间序列预测模型等。后来又在此基础上引入了卡尔曼滤波[7-13]、小波分析[14]、灰色系统[15-17]等方法进行公共交通领域内的时间序列预测，这些预测方法相比传统的回归模型预测精度的预测稳定性都有了较大的提高，但在对公交客流数据本身的利用方面还不够充分，实际使用中的预测有效性也得不到保证。

2006年后神经网络的应用开始逐渐进入交通领域，国内罗海燕等[18-19]比较早地将BP神经网络模型应用到公交线路站点时段上下车人数预测中,之后BP神经网络及相关的改进算法开始在交通领域内井喷式发展，BP神经网络算法在地铁、公交及货物运量等短时预测领域有着出色的表现，王立政等[20-26]发表了一系列相关的论文。除了BP神经网络外，被广泛应用于短时客流预测的还有RNN以及RNN的变体LSTM长短期记忆神经网络等。LSTM相比于RNN模型多引入了一个记忆存储单元，它的功能是自动过滤网络结构中的无效成分并长时间自动记忆输入的有效成分，YANG等[27-31]认为这有效解决了RNN在反向传播过程中的梯度爆炸问题，因此实际使用过程中LSTM更适合用于时间序列类数据的分析。除了神经网络模型外，孙德山等[32]在国内首次将SVR用于混沌时间序列的预测。杨军等[33]又将LSSVM(最小二乘支持向量机)方法开创性地用于轨道交通客流预测。

Leo Breiman和Adele Cutler提出并拓展了随机森林算法，起初这项算法只是作分类使用，后来人们逐渐开始意识到它在预测方面的作用。YAO等[34]使用了随机森林来预测公交到站时间。

深度学习类算法如LSTM对客流预测有较好的精度，但是需要的训练样本过大，模型拟合成本过高(设备、时间)，而支持向量机类算法预测精度不够。对于短时公交客流预测，不仅需要比较高的预测精度，还要尽可能简化对客流特征的处理过程。Catboost算法在训练模型时能够将公交客流离散化特征(如用户ID、IC类型等)进行自动转化为数值特征，此过程大大节省了特征处理的时间。此外，由于使用了对称树结构，Catboost算法的效率和泛化性能也优于传统的GBDT类算法(Xgboost、LGBM等)。本文通过Stacking框架将LSTM和RF算法作为第一层的基学习器，提取公交客流数据更强的特征信息，将Catboost算法作为第二层预测模型。以广州市104和565路公交作为算例验证S-Catboost模型的实际性能，预测客流量能够较好地为公交调度和居民出行提供决策依据。

1 模型理论

本文旨在通过构建一种基于Catboost方法的堆叠模型，对比以往的单一GBDT类模型，它能够提高模型的解释能力和预测性能，从而更加精确地进行短时公交客流预测，并且更加深入地分析多源数据中不同影响因子和预测客流之间的关系。

1.1 Cart回归树

Cart(分类和回归)树是一种采用二分递归分割技术产生的决策树，即二叉树，对于某个特征A而言，不管A的属性是离散还是连续，所产生的内部节点分支都只有2个。如果Cart树进行决策的标签变量为连续值，则产生的树为回归树；如果Cart进行决策的标签变量为离散值，那么产生的决策树为分类树。

Cart回归树的算法流程如下：

Step 1:假定S为一组具有连续属性标签的数据集S={(x1,y1),(x2,y2),(xn,yn)}，其中x为特征变量数据集，y为标签属性数据集。

Step 2:构建损失函数fj,k，fj,k表示某个(j,k)组合下对特征集x进行划分并计算得到的损失，然后对特征变量划分组合空间(j,k)进行遍历得到损失函数最小的(j,k)组合，作为构建第一层回归树的依据，其中Rm是输入空间，cm是输入空间对应的输出值。

(1)

Step 3:用给定的(j,k)对划分区域并求出相应的输出值cm·Nm为对应划分区域内的样本个数。

R1(j,k)={x|xj≤k},R2(j,k)={x|xj≤k}，

(2)

(3)

Step 4:构建第一层决策树，利用上一步结果求出cm，得到第一层决策树T1。

(4)

(5)

1.2 Boosting方法

Boosting方法属于集成学习(ensemble learning)的一种，实质上是基于多个基分类器对训练集的判断，通过加法模型将这些基分类器组合得到最终的强学习器的过程。对于一类弱可学习的二分类样本S={(x1,y1),…,(xi,yi),…,(xn,yn)},i=1,…,n，样本中xi∈R,yi∈{-1,1}。我们使用Boosting方法将弱分类器通过加法模型组成强学习器。

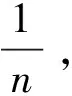
(6)

Step 2:对于j=1,2,…,J，进行(b)至(d)过程的迭代(J由最终构建的分类器分类失误率决定，最终分类无误差时迭代过程结束)。

① 对于具有权值的分类样本使用弱学习器(如Cart树模型等)进行学习，得到基分类器Gj(x)。

Gj(x)∈{-1,1}。

(7)

② 计算分类误差率ej。

(8)

分类误差率反映了每一代分类器的分类效果，由每个数据样本的分类结果和数据对应的权重之积累加而成，其中I()为指示函数，括号中的内容为真，则返回1，反之则返回0。这一步旨在突出被分类器误分类的样本点，样本被误分类时对应的权值会增大，反之则减小。

③ 计算分类器的权重系数αj。

(9)

对于一个弱可学习的样本，ej≤0.5，αj随着ej的减小而增大，保证了分类误差率越小的学习器在最终决策中的影响力越大，使学习结果能够收敛。

④ 更新样本S的权重矩阵。

(10)

Dj+1=[wj+1,1,…,wj+1,i,…wj+1,n]。

(11)

Step 3:构建分类器的线性组合函数f(x)。

(12)

上述过程可用如图1所示的流程图形象描述。

图1 Boosting过程Fig.1 Boosting process

1.3 GBDT原理

GBDT(梯度提升树)属于集成学习中Boosting家族范畴内的一员，其学习机理为通过迭代的方式构建m棵子决策树h(x;a1)，…，h(x;am)，最后通过加法模型和Boosting方法将它们组合成最终的GBDT模型。其中第n棵子树的表达式为

Fn(x)=Fn-1(x)+vβnh(x:an)，

(13)

式中，Fn-1(x)代表第1棵子树到第n-1棵子树的累加之和;βn代表第n棵子树的权重;v(v∈(0,1))代表步长。

Step 1:初始化学习器。

(14)

Step 2:对于m=1,…,M(M表示迭代次数，即弱学习器的数量)不断迭代分类器。

① 计算损失函数的负梯度在当前模型的值并将它作为残差的估计值。

(15)

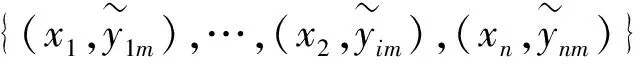
③ 通过线性搜索的方式计算j=1,2,…,J每个叶子节点最佳的拟合值。

(16)

④ 更新回归树

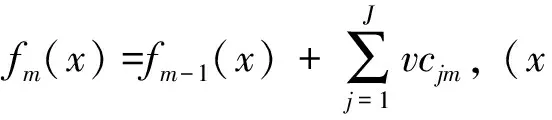
(17)

Step 3:得到最终的强学习器。

(18)

1.4 Catboost原理

Catboost总体算法框架与GBDT一致，但是在处理类别特征、Boosting方式以及决策树生长评分方面作了比较大的改进。这三个改进令Catboost能够有效地处理字符串特征，并且相同数据规模下的模型拟合速度要快于Xgboost和LGBM。

① 类别特征

Catboost的基础仍是提升树，与传统的梯度提升树不同的是Catboost在处理类别特征时，没有简单地采用基于贪婪目标统计的方法进行分裂节点的选择。而是创造性地在计算节点增益时考虑先验分布项，有效地排除了类别变量中低频率特征和噪声对生成决策树带来的影响。

(19)

式中，σj为第j数据;xi,k表示训练集中第i行数据的第k列离散特征;a是一个先验权重;p是先验分布项(对于回归问题而言，先验项一般取训练集中预测标签的均值；对于二分类问题而言，先验项取值为正例也就是为1的项的先验概率);这里的[]为指示函数，满足内部条件则输出1，否则输出0。

通过改进后的TS方法，Catboost能够在信息损失最小化的情况下将类别特征转化为数值。

(2)排序提升(Ordered boosting)

传统的GBDT模型采取的是无行列采样的方式，所有的基学习器及即Cart决策树是在一个完整的数据集上进行梯度提升的，每次迭代都使用上一轮树的负梯度进行训练。这样会导致预测偏差(bias)不断累积和过拟合(over fitting)的现象。Xgboost和微软开发的LGBM采用了行列采样和正则化的处理降低了过拟合的效应。Catboost更进一步提出了Ordered boosting方法。算法伪代码如下：

Algorithm:Orderedboosting

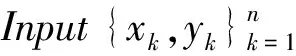
ordered according to σ,the numbers of trees I

σ←randompermutationof[1,n]

Mi←0fori=1ton

foriter← 1toIdo

fori← 1tondo

forj← 1toi-1do

M←learnatree(Xj,gj)

Mi←Mi+M

returnM1,M2,…,Mn

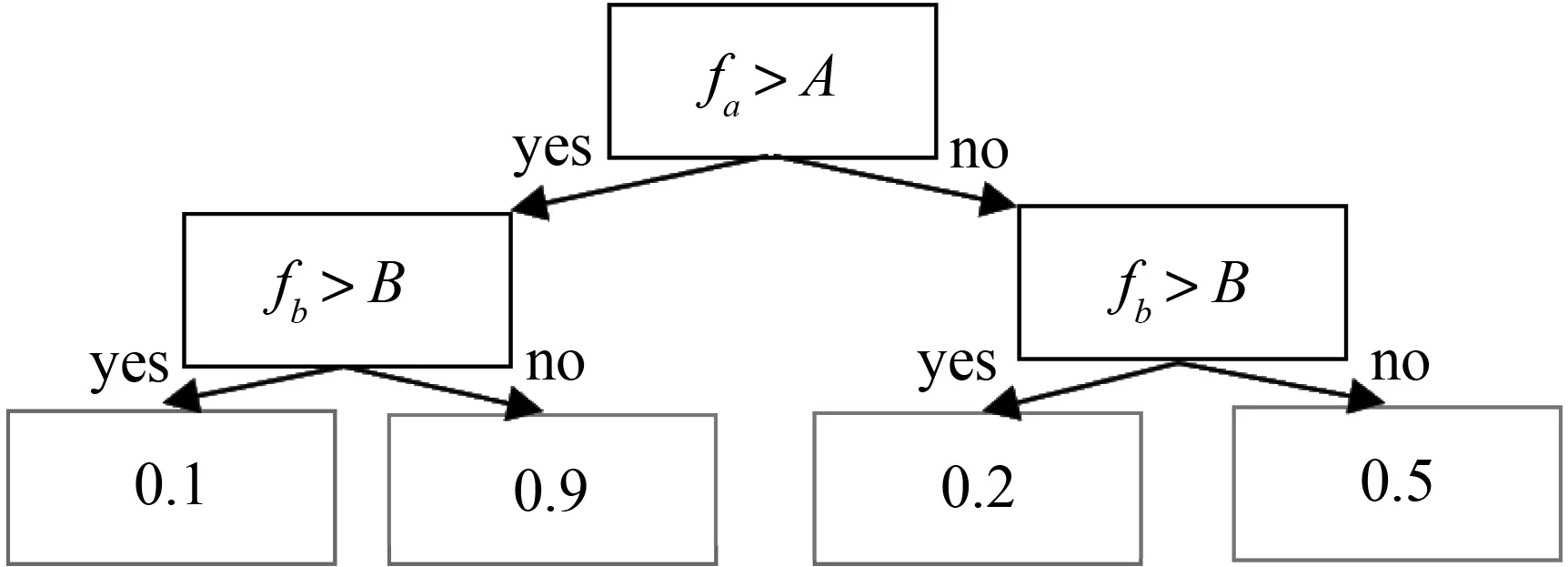
图2 完全对称树ODT的结构Fig.2 Structure of complete tree ODT

其中，σ是训练集随机排序的次数；I为需要生成对称决策树的数量也就是学习器的个数。

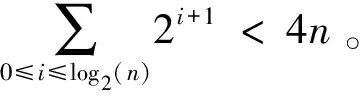
③ 快速评分

Catboost使用完全对称树(oblivious decision trees，ODT)作为基学习器，它的结构如图2所示，与一般决策树不同的是，完全对称树对于相同深度的内部节点，分裂时选择的特征以及特征阈值是完全一致的。所以完全对称树也可以变换成具有2^d条目的决策表格，d表示决策树的层数。这种结构的决策树更加平衡并且特征处理速度远快于一般的决策树。此外，通过将浮点特征，统计信息(用户id等)、独热编码特征统一用二进制处理，模型的大大减少了调参需求。

④ 特征重要度排序

Catboost不仅有较高的预测精度，而且同时能够能够甑别不同影响因子(即预测所使用特征)对预测结果的相对贡献度，某个特征在单棵决策树中的相对贡献度用以下公式衡量。

(20)

式中,M为迭代次数(树的数量);Jj2代表特征j的全局重要度。

(21)

式中，L为树的叶子节点数量;L-1为树的非叶子节点数量;vt是和节点t相关联的特征;it2是节点t分裂之后平方损失的减少值，it2减少的越多说明此次分裂的收益越大，意味着此特征对于所属节点的特征重要度越高。

1.5 Stacking原理

随着互联网和各种检测技术的发展，在交通领域运用多源客流数据进行客流预测和分析逐渐成为一种趋势。这些多源数据可能包含数个到数十个离散和连续的特征,单一机器学习模型对这类多源数据的处理效果很难达到极致。为了更充分地发挥这些模型本身的潜力，本文需要使用某种方法对多源客流数据进行处理，使得不同特征状态下的客流具有更加明显的差异。堆叠(stacking)方法是一种采用多层次的模型进行特征生成和模型融合的方法，通常采用数个基模型作为第一层的输入，将输出的预测结果作为新特征加入到第二层模型的特征矩阵中，最后使用次级模型进行预测，以期得到更高的预测精度。理论上stacking的层数没有限制，但是超过两层后继续stacking的效果十分有限。Stacking的流程如图3所示。

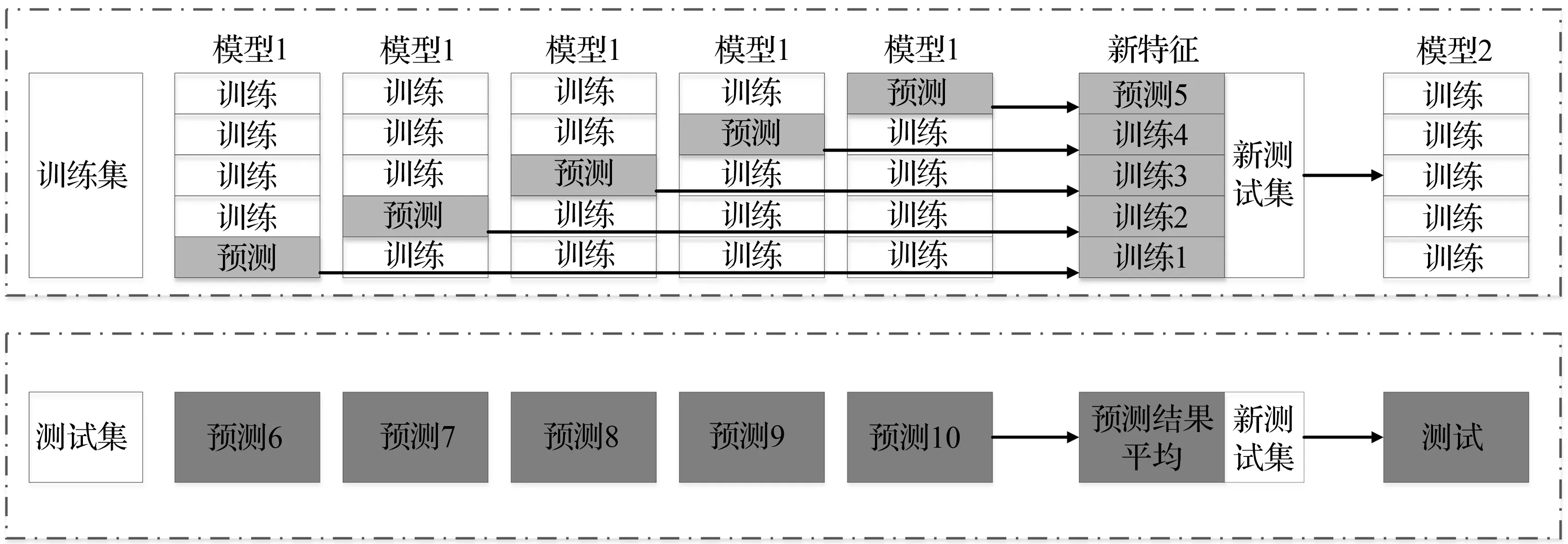
图3 Stacking过程Fig.3 Stacking process

首先，将原始数据集按照一定的比例划分为训练集和测试集。其次,利用5折交叉验证的方式使用基模型对训练集的5个部分分别进行预测。最后再对测试集进行预测。经历这样的5次“训练-预测”过程后，得到了图中的“预测1-预测5”和5个测试集的预测结果。将“预测1-预测5”按照对应的顺序组合，并把测试集的5次预测结果均值求出来，最后合并为一列新的列向量，作为新特征添加原始数据中。若采用的基模型不止一个，则重复上述过程，不断生成新的特征。接下来使用第二层模型作为次级模型，对基模型产生的结果进行训练并得到测试集的最终预测结果。

在Stacking方法中，采用的基模型数量没有限制。但是更多基模型意味着总体模型的训练时间将会大大增加。此外不同基模型之间要有差异化并且预测能力要大体相近，否则stacking之后第二层模型的预测精度可能反而低于单独使用某一种模型时的预测精度。基于上述考虑，本文使用了的LSTM和RF作为本文双层堆叠的基模型。分别对两种模型进行stacking 操作，使用第二层的Catboost模型对新数据进行预测和分析，得到最终的结果。

2 实例

2.1 数据来源

本文所选用数据集为广州市104路和565路的小时公交客流数据，如图1所示。104路选用的数据集为6至8月份刷卡数据，565路选用的数据集为10至12月刷卡数据。两条线路均保留最后一天作为测试集。均保留广州市104路公交起点在中山八路总站，终点为海印桥总站，全长8.8 km。565路则以大学城总站为起点、穗盐路总站为终点，两条路线具体位置如下所示：

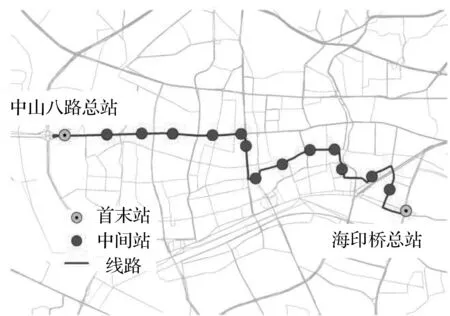
(a) 104路

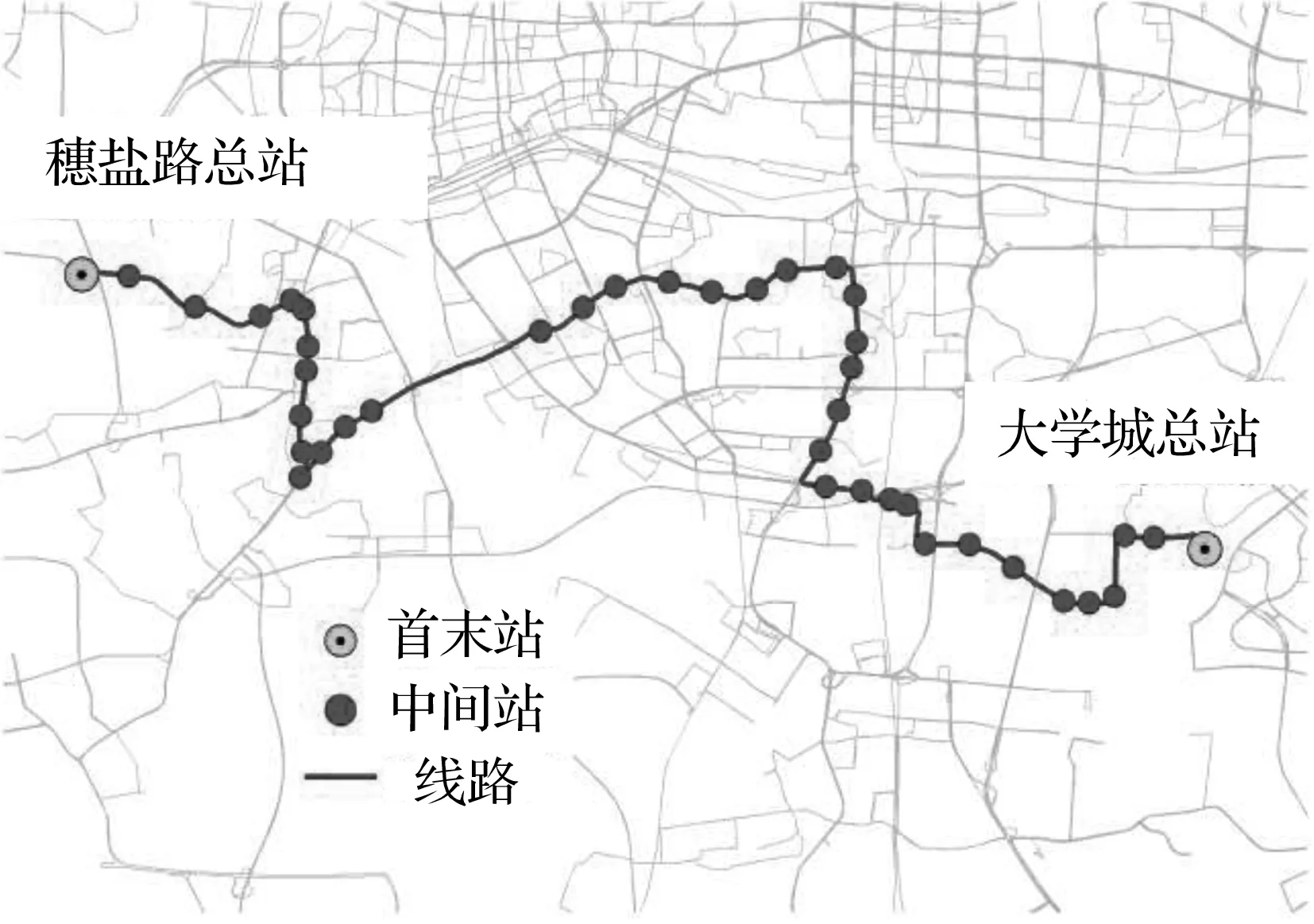
(b) 565路

表1 104、565路客流情况Tab.1 Passenger flow of 104 and 565

2.2 影响因子提取

对于某一个城市，影响公交客流的外部性因子有很多，但总体而言可以分为3类。

第一类是时间性指标。众所周知，公交客流随着时间的变化呈现明显的潮汐性波动。在一天中不同时段，不同季节公交客流的变化都会呈现不同的规律。

第二类是天气指标，分别有日最高温度、日最低温度、降雨量等级以及空气指数等因素，这类指标会对某段时间公交客流变化趋势造成持续性影响，特别是会对非通勤类交通需求所属的那部分客流产生较大的影响。

第三类是节假日指标，包括是否双休日、是否法定节假日等。中国的一些重大节假日(五一劳动节、国庆节等3 d以上的长假)会对某个地区的公交客流造成重大影响，使部分线路的公交客流断崖式下跌或爆发性增长，对原有的客流变化规律产生巨大的扰动。这些因素通常会为公交客流预测带来很大的难度。

本文针对选用的广州市两条公交客流数据，分别从时间、天气和节假日类因素考虑，选用了共10种和公交客流波动密切相关的特征进行分析。这些特征及具体含义见表2。

表2 公交客流特征名称及含义Tab.2 Name and meaning of characteristics of bus passenger flow

3 研究思路

本文的研究思路和模型总体框架如图5所示。第一部分是数据预处理过程，将原始公交客流数据经过清洗和特征提取后进行标准化处理，并划分为训练集和测试集。第二部分是利用Stacking方法提取新特征，并将产生的强关联特征添加到特征部分，生成新的数据集。第三部分是使用Catboost方法对新数据集进行预测，得到最终的预测结果，然后与几种常用的机器学习算法进行对比，验证本文提出模型的优越性。

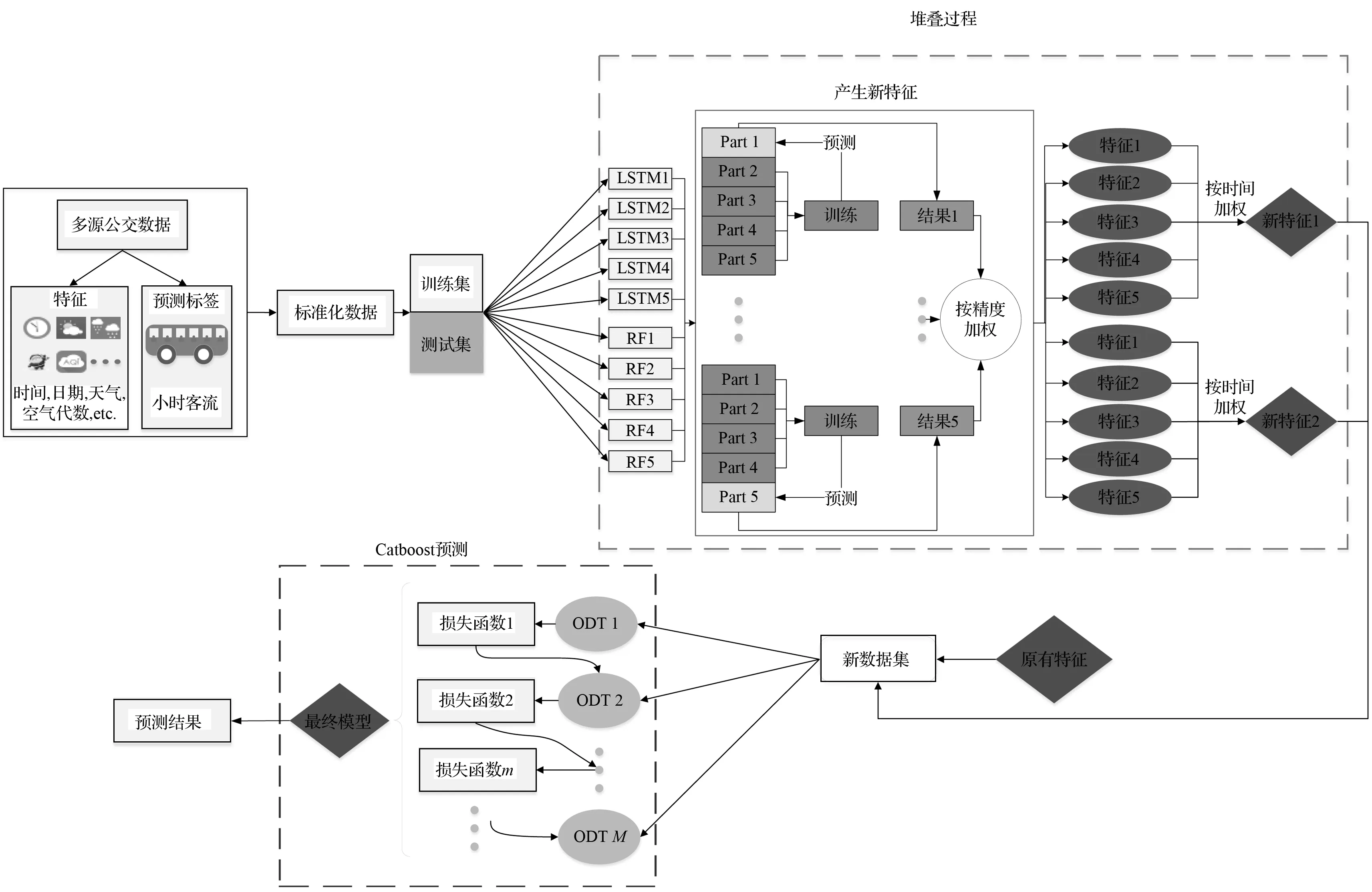
图5 总体框架Fig.5 Overall framework

4 结果与讨论

4.1 超参数优化

在本项研究中，为了获得较好的预测效果，需针对预测数据集进行超参数优化，寻找与本项研究所使用数据最佳的参数组合。本文选用了3个超参数：C(最大树深度)、M(基学习器数量)和ε(学习率)对模型进行优化，具体参数见表3。本文将所使用数据集划分为训练集和预测集两部分.首先使用训练集进行超参数优化，得到最佳参数组合。然后使用测试集检验模型性能。本文通过构建初始参数空间并利用网格搜索的方法对参数空间进行网格搜索找到最优参数组合。

表3 超参数描述Tab.3 Hyperparametric description

为了更好地发挥Catboost模型性能，需要对上述3个参数进行网格搜索优化。同时，为了避免优化后的参数组合在训练集中过拟和，本文使用5折交叉验证的方式计算不同参数组合下模型的测试分数。最后选择测试分数最高的那组参数建立模型。

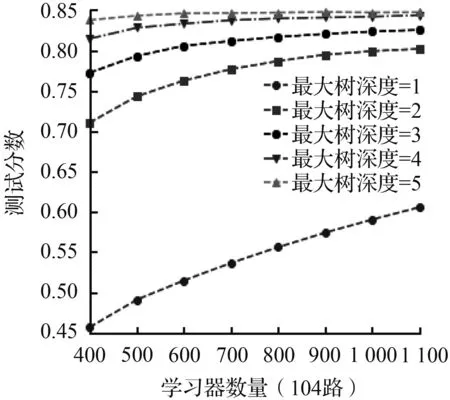
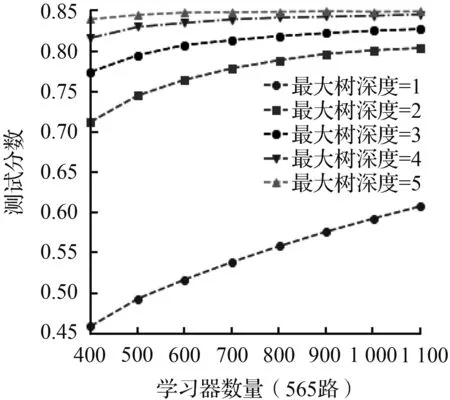
(a) 学习率=0.008

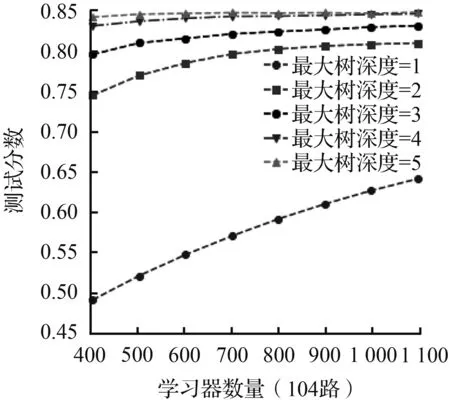
(b) 学习率 =0.01

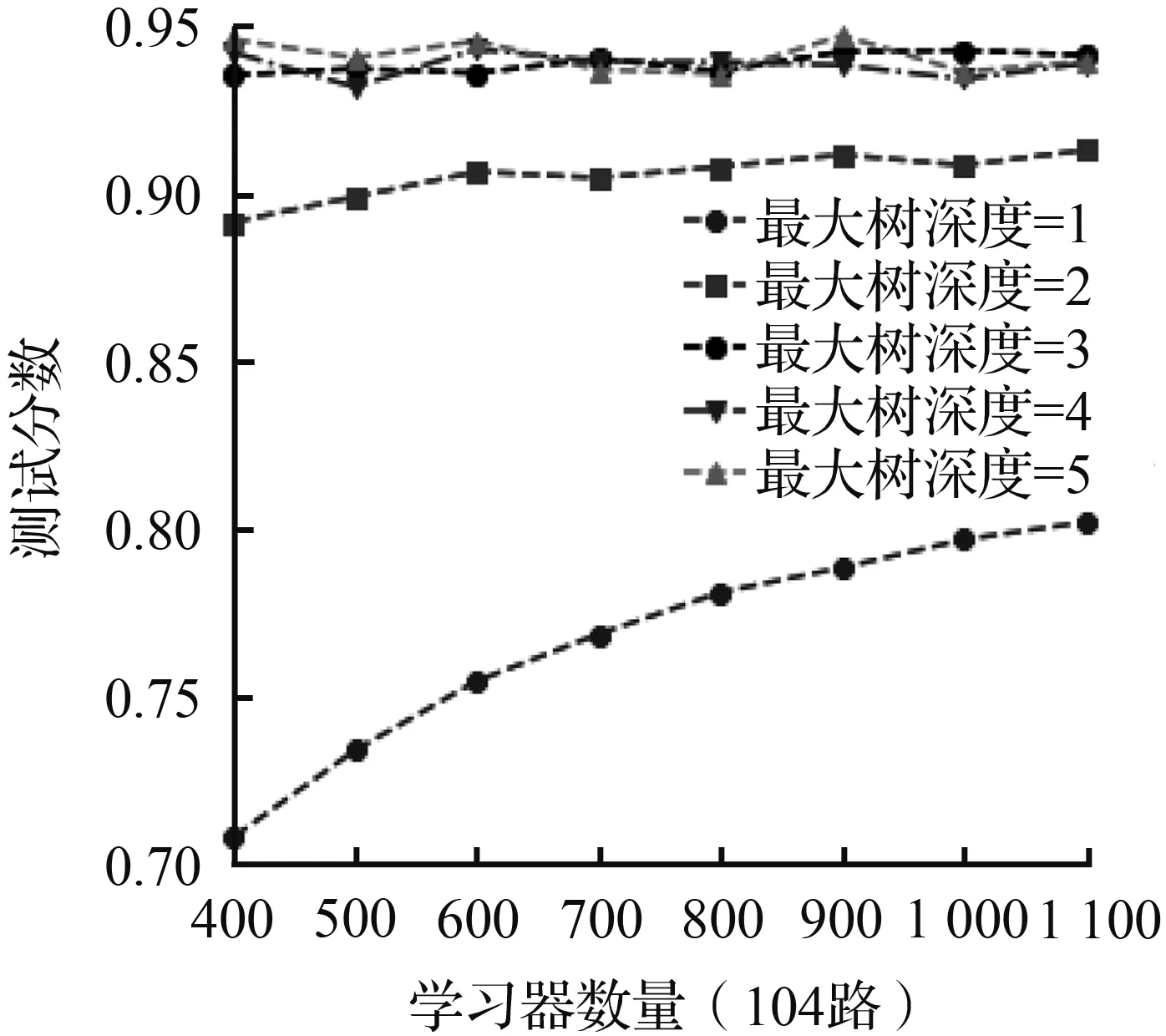
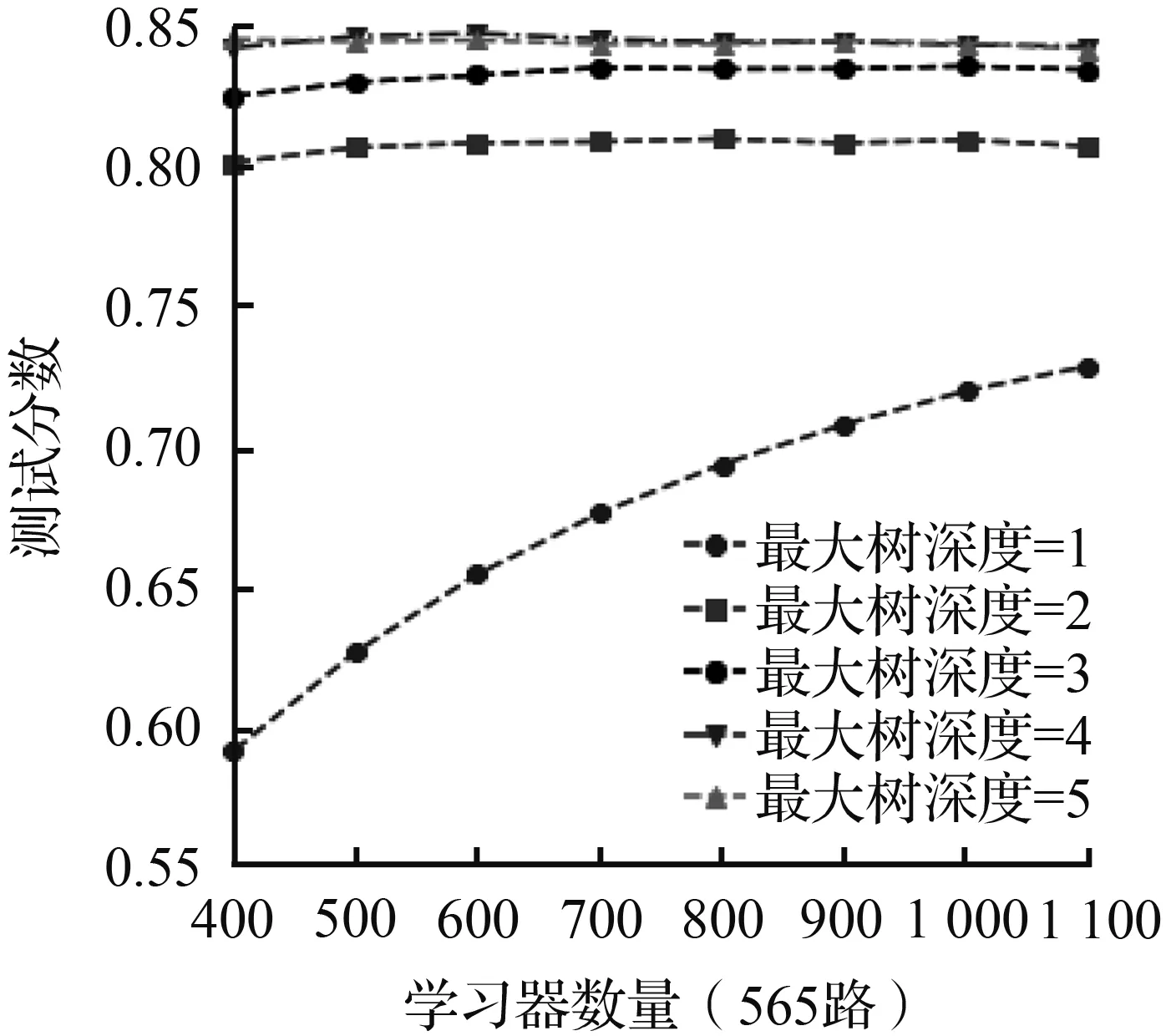
(c) 学习率 =0.02

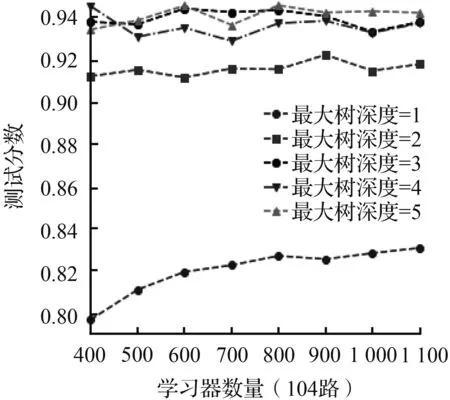
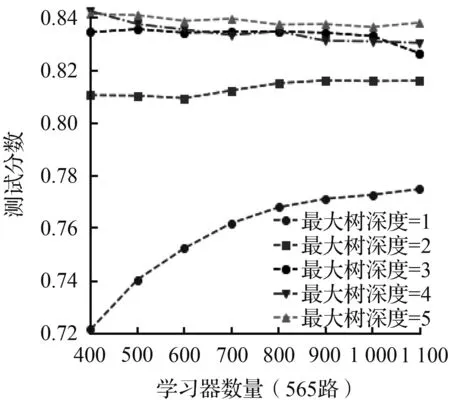
(d) 学习率 =0.05

调参结果的平均测试分数随着不同的“最大树深度”、“学习器数量”以及“学习率”三个参数变化的情况如图6所示，从图6中可以看出“最大树深度”对模型的预测精准度影响最大。对于104路而言，当“最大树深度”由2上升到3时，模型的测试分数有了7%左右显著的提高，但是随着“最大树深度”继续增加到6，测试分数只提高了不到2.5%，甚至有着略微的下降，并且565路也有着类似的表现。这表明应根据问题的规模构建决策树的最大搜索深度，太小的“最大树深度”会抑制决策树向下分支，导致构建的决策树拟合效果不足；而足够大的“最大树深度”虽然能够在训练集中很好地拟合数据集，却会造成“最大树深度”catboost模型与训练集过拟合导致模型在测试集中泛化性能不足。而学习率从0.008增大到0.05时可以发现，104和565两条线路的模型达到收敛条件所需的“学习器数量”越来越少。并且当学习率越小，模型的最优测试分数会略高一些。据此分析，学习率越小意味着“最大树深度”catboost模型在梯度下降时的搜索步长越小，得到最优的损失函数值的几率越大，而学习率越大，错过最优解的几率就越大。然而，越小的“学习率”虽然能得到较好的训练分数，但是意味着要增加更多额外的树和消耗更多的计算资源。因而学习率的实际选用因同时兼顾两方面的因素。在“学习器的数量”和“学习率”之间找到一个平衡。对于两条线路而言，随着“学习器数量”的增加，不同“最大树深度”和“学习率”下的测试分数都有了一定的增加，直至模型充分拟合，测试分数基本平衡。

4.2 模型对比

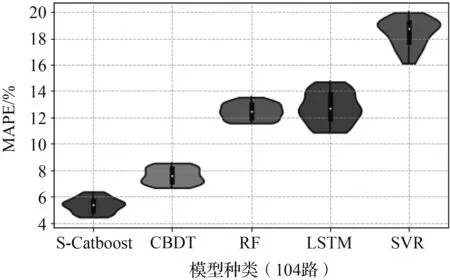
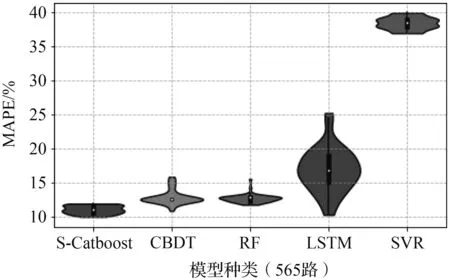
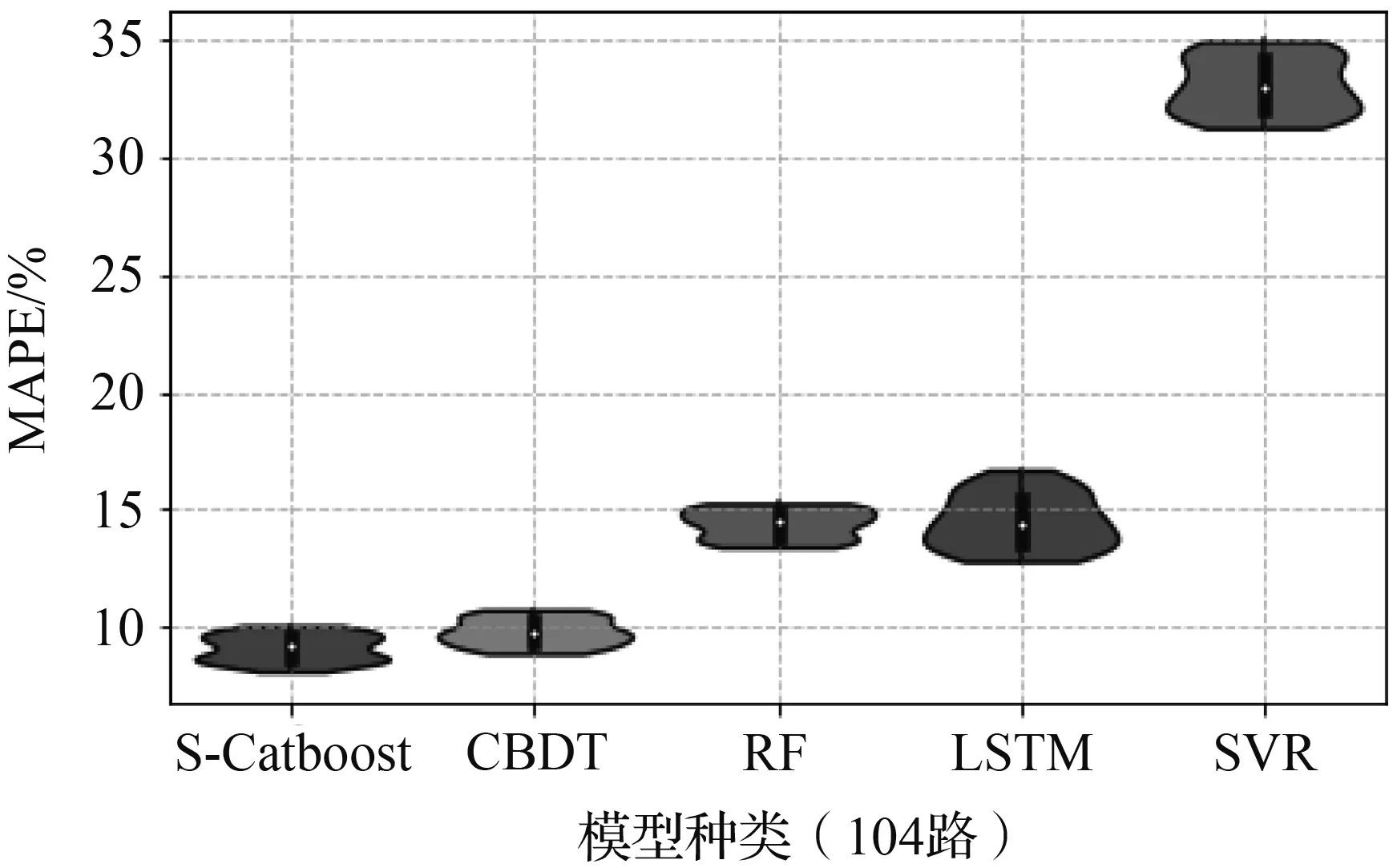
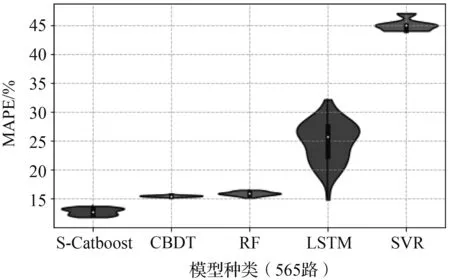
为了更好地显示S-Catboost模型的预测性能和泛化能力，分别使用LSTM、RF、SVR和原始GBDT模型等4种预测模型进行对比。本文采取相对指标MAPE作为预测结果精度的评判标准，将上述5种预测模型分别运行50次，得到各个模型在分别在单步、双步和三步预测条件下的日平均预测误差分布情况并制成violin图，图7为5种不同模型在最优参数条件下的预测精度、稳定性情况。

(a) 步长=t-1

(b) 步长=t-2

(c) 步长=t-3

从图7中可以看到5种模型在不同预测步长条件误差离散程度，以此观察不同模型的预测稳定性。对于104路，显而易见5种预测模型的预测精度呈现阶梯状分布。第一梯队的模型有Stacking、GBDT，第二梯队的模型有RF、LSTM，第三梯队的模型有SVR。上述三个梯队的模型不仅在预测精度方面存在明显的差别，在预测误差分布情况方面同样如此。此外，GBDT类模型的预测精度要明显优于另外两个梯队的模型。值得一提的是，在时间步长由1增加到3时，S-Catboost较传统GBDT模型的预测精度都有所领先，特别是对于客流数据相对不平滑的565路。尽管随着时间步长的增大，这种精度上的优势逐渐缩小。这仍然能够显示S-Catboost对处理多源数据的进一步挖掘能够有效地降低预测误差以及抵抗时间步长增大对预测的不利影响。

对于565路，情况与104路略有不同。565路5种模型的预测误差呈现为两个层次:SVR模型和其他模型。在3种预测步长下，SVR模型因为565路本身的数据波动而表现远不如其他几种模型.更多的是，565路LSTM模型多次运行的结果远不如104路稳定，这一点极大概率是由于565路的测试集中第23个小时的小时客流只有106人，LSTM对这个小时的预测极不稳定。造成上四分位数、下四分位数差值达到了15%以上。

4.3 影响因子排序

在利用S-Catboost模型对短时公交客流进行预测时,我们不仅关注它在预测性能方面的高精度和稳定性,更关心各种影响因子对公交客流预测的全局重要性。了解不同影响因子在实际客流变化中所起的贡献度在现实客流预测场景中极为重要。相关部门可根据实际客流情况寻找到最适合的影响因子组合,提高客流预测的效率。

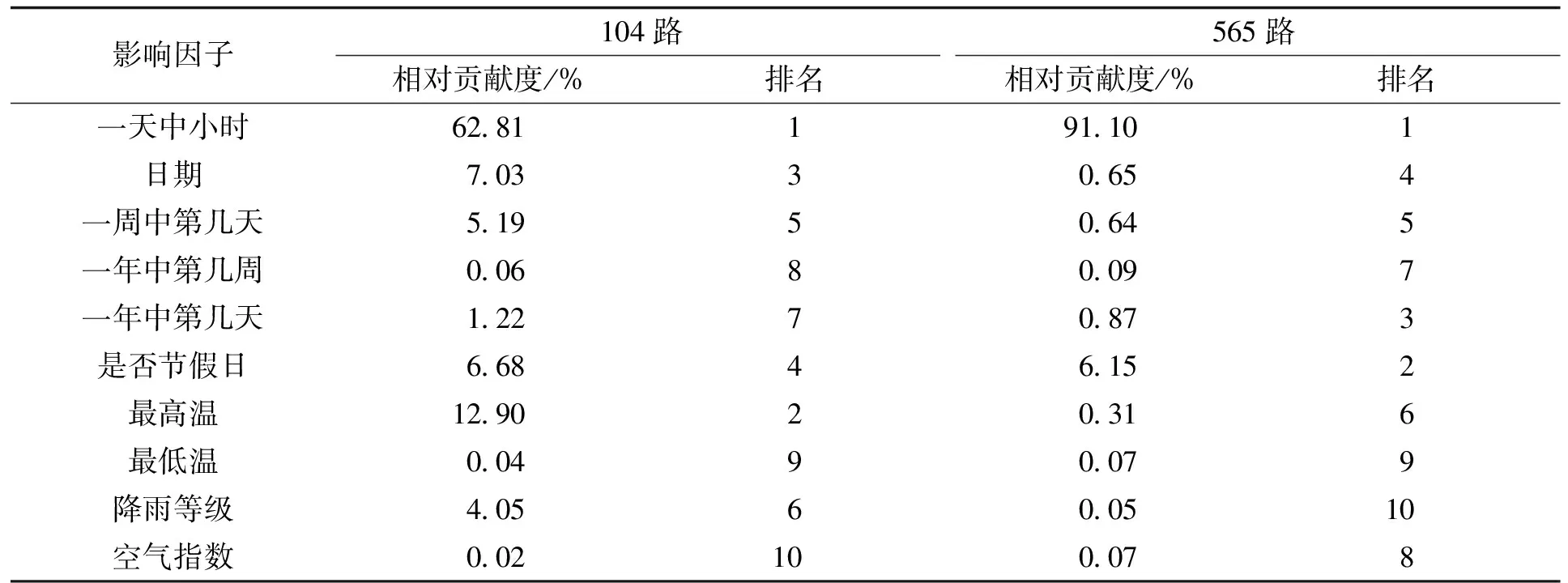
表4 影响因子重要度排序Tab.4 Importance ranking of influence factors

影响因子重要度排序见表4，从表4可以看到，整体而言,无论是104路或者565路时间类变量对预测客流的贡献度要大于天气类因素。具体来看,对于104路和565路影响最大的变量为“一天中小时”，它的贡献度分别是62.81%和91.10%。这一点验证了历史小时客流数据在客流预测中无可替代的作用。这是因为对于一条公交线路，客流的波动和一天中的时间变化息息相关，客流变化呈现明显的周期性。除了时间因素，我们可以看到，节假日类因素“是否节假日”在104、565路客流预测中的重要度均在前4以内。这说明节假日因素在客流变化中的地位也十分重要。与“一天中小时”不同，节假日类变量影响通常在周及以上的时间跨度才会比较明显的体现。除了固定的周末节假日，还有众多时间不固定的特殊节假日，在这些节假日时间段内，公交线路的客流与相邻时间区间通常有较大的差异，对于公共交通部门进行客流预测和分析时考虑这个因素至关重要。除了节假日和时间类因素，我们同样对天气因素对客流预测的影响感兴趣，对于104路，“最高温”对客流的影响因子为12.90%,位居第二，并且远高于565路，因为104路的数据在4至6月搜集，白天的炎热程度对居民出行方式选择影响巨大，565路的数据主要集中在冬季，气温的影响相对要小得多。广州夏季十分炎热，一天中的“最高温”过高会使通勤客流转乘地铁的比例升高，并且极端高温会使乘客可忍受候车时间变短，进而降低公交乘客的出行欲望。降雨量对通勤客流影响较小，主要影响的是娱乐、购物等客流的出行情况，由于这两条线路的通勤客流比例都较高，导致降雨量对总体客流的影响并不明显。

4.4 偏效应分析

除了对不同特征对预测结果的重要度进行排序，我们还关注这些不同类别的特征对预测标签的内源性影响，本文使用偏效应项(即将其他影响因素边缘化之后，考虑其中某个单一特征的变化对预测目标的变化趋势所造成的影响)对不同特征进行偏效应分析。考虑文章篇幅，对4.3节中特征重要度排序种筛选出的贡献度比较高的几个影响因子做了偏效应分析，具体结果如图8、图9所示。

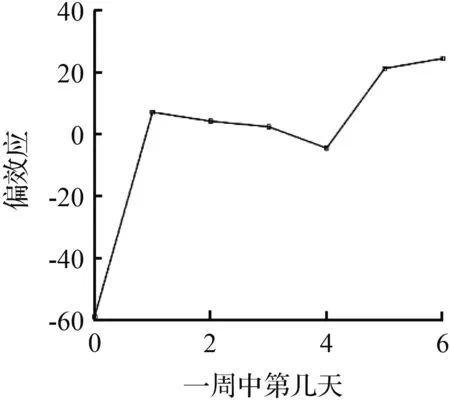
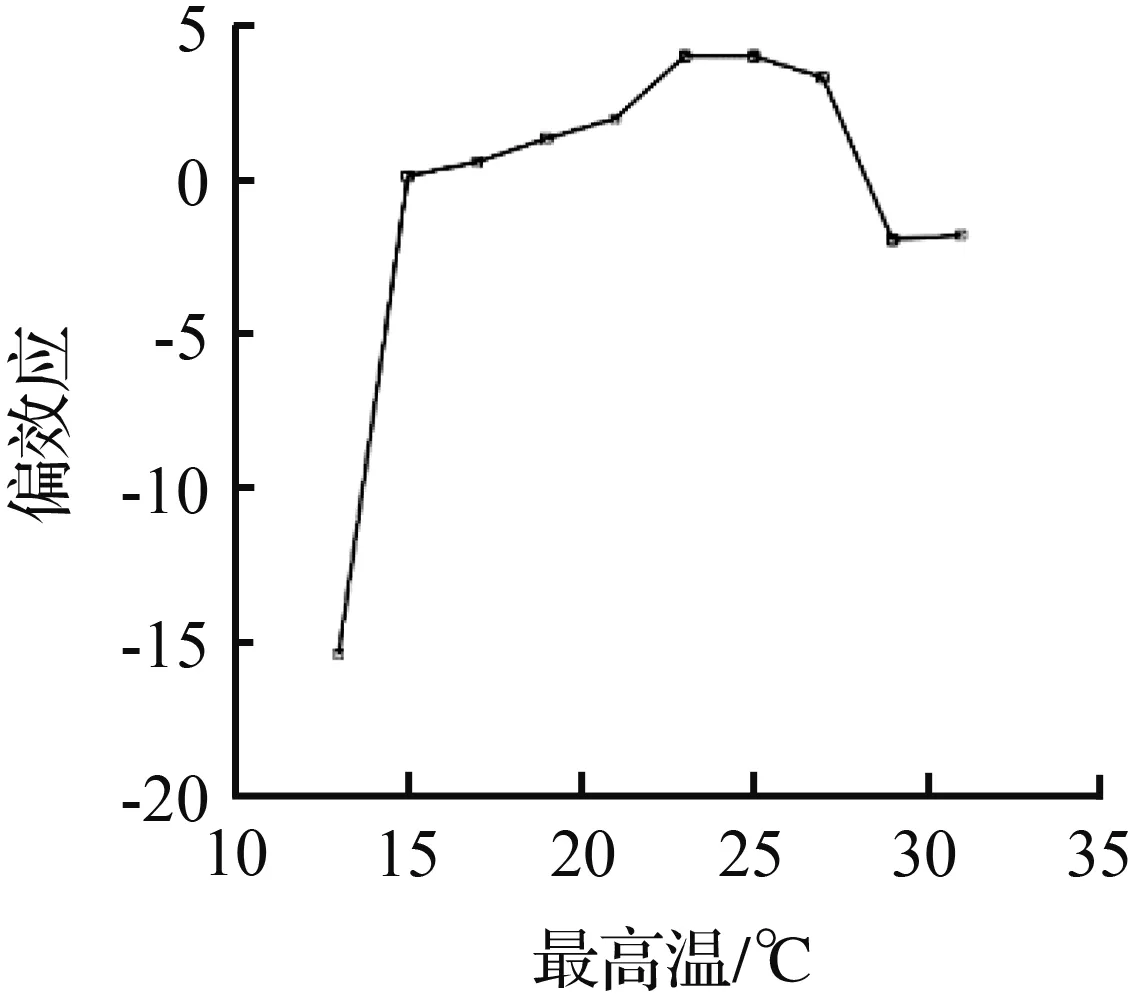
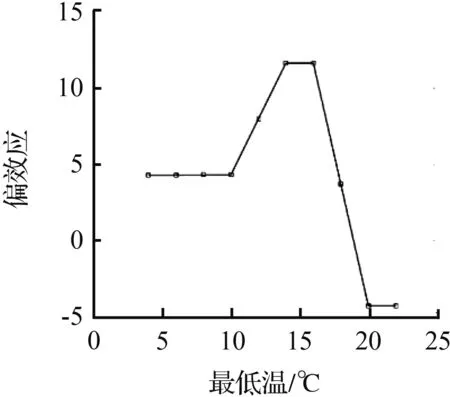
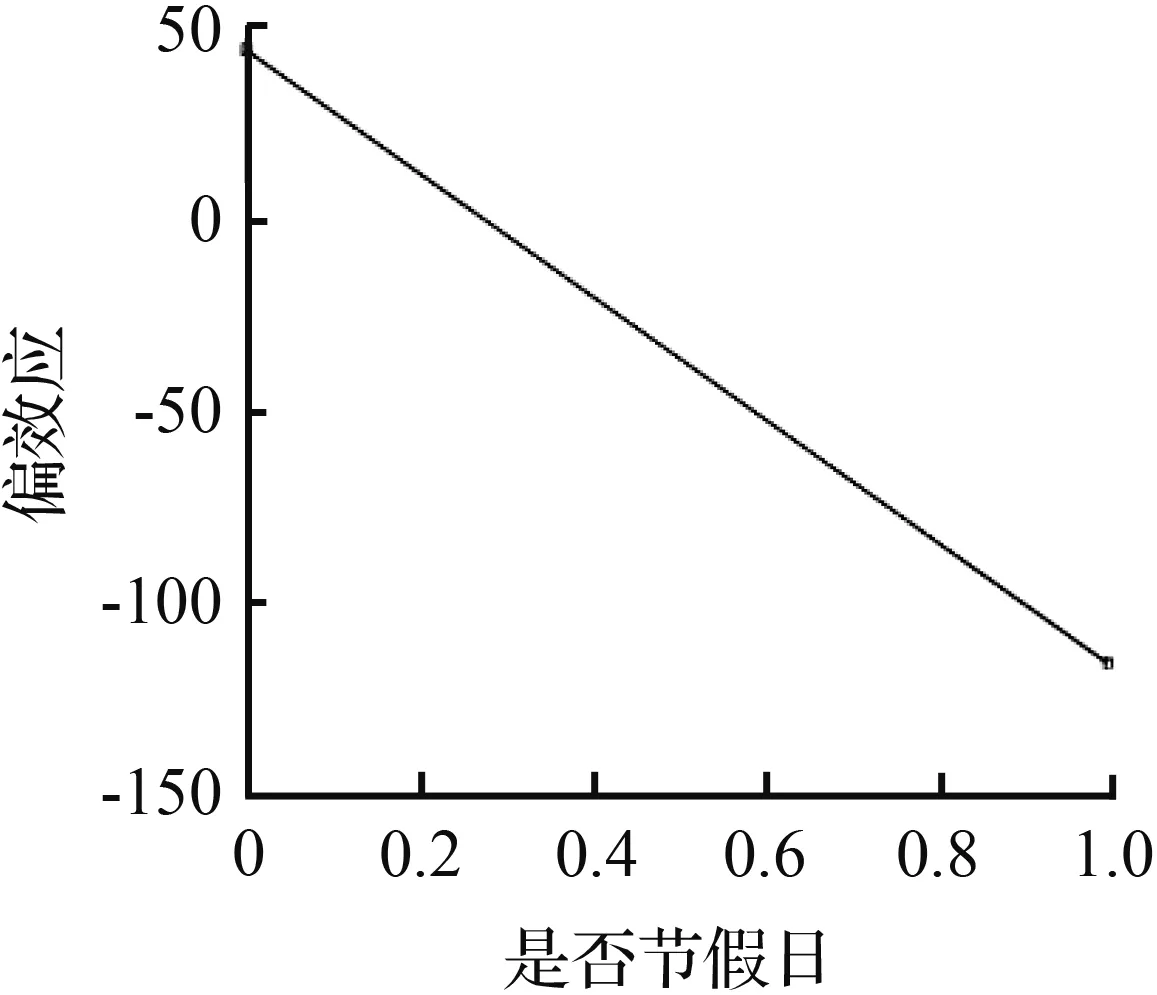
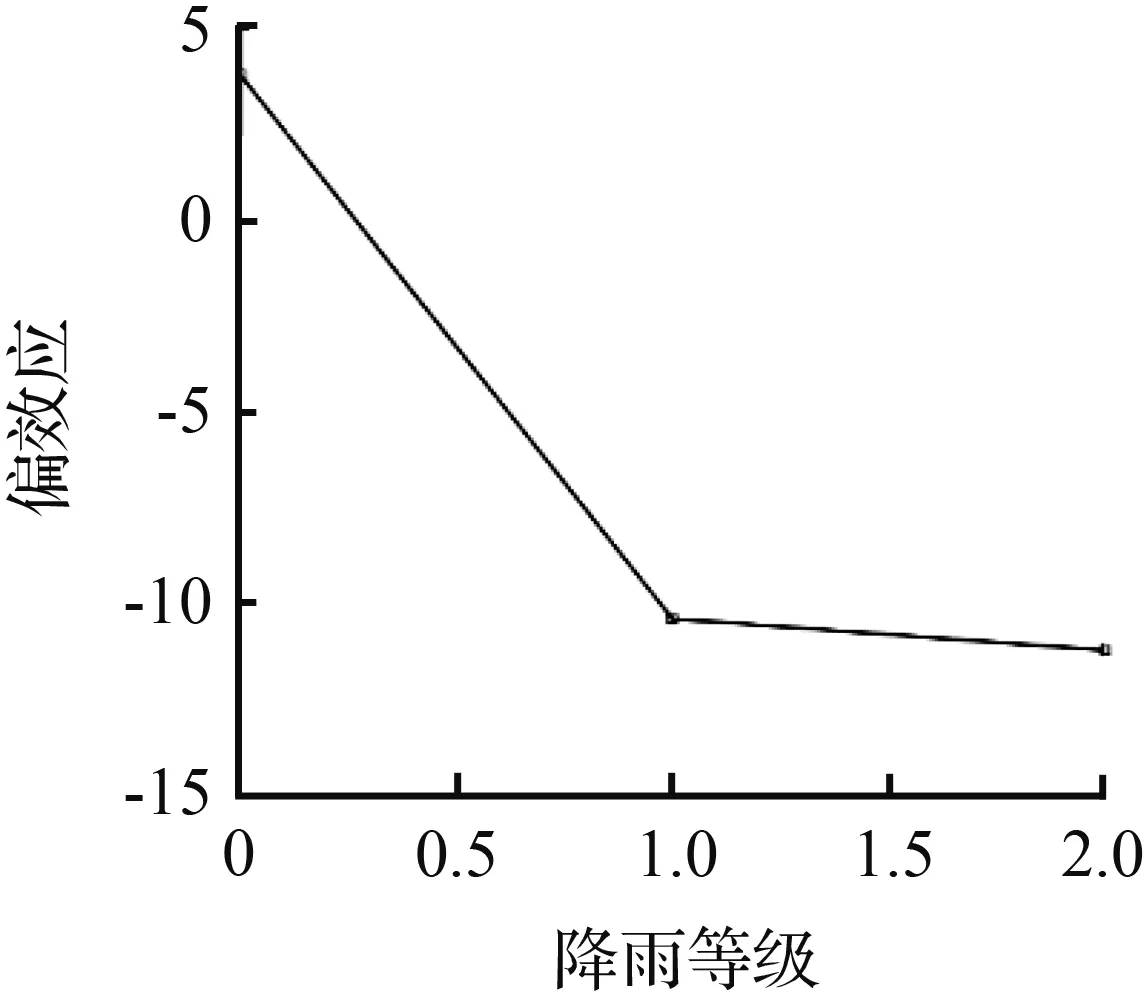
图8 104路几个影响因子的偏效应Fig.8 Partial effect of influence factors on line 104

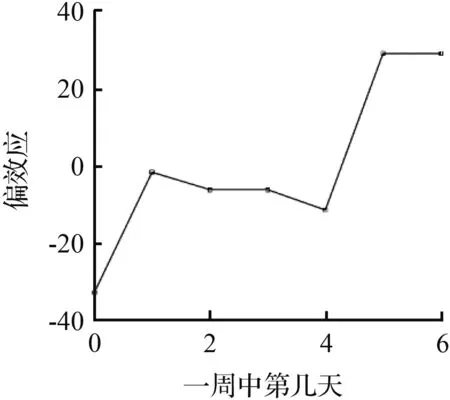
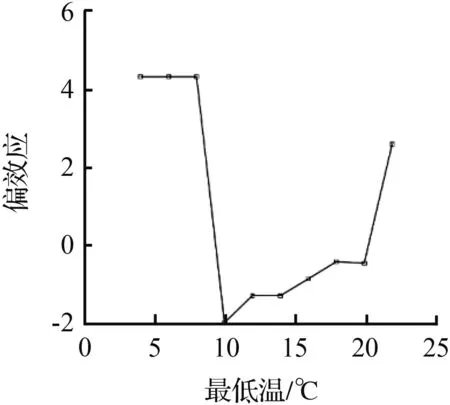
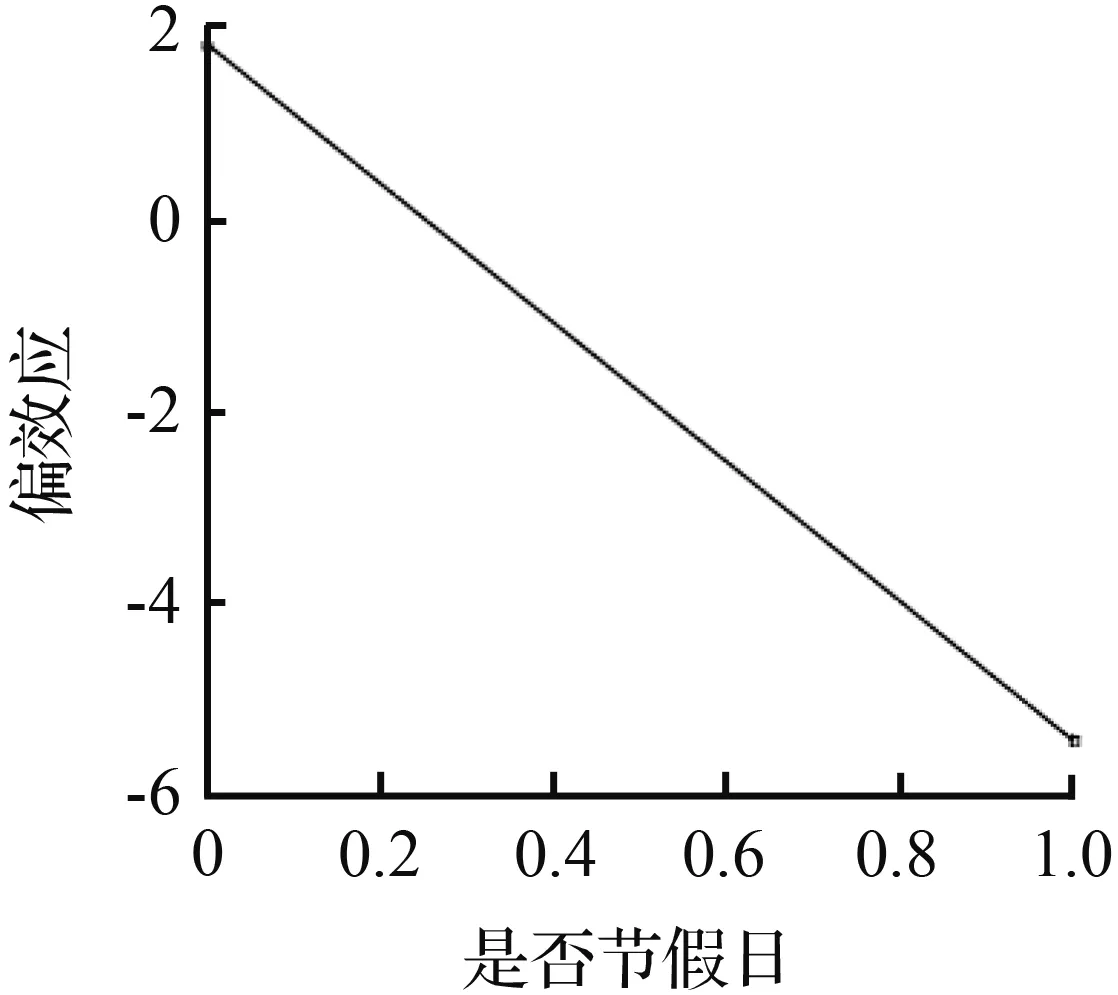
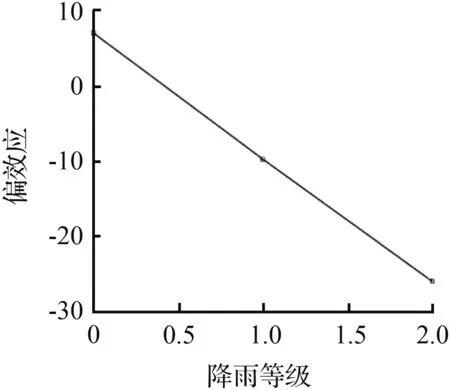
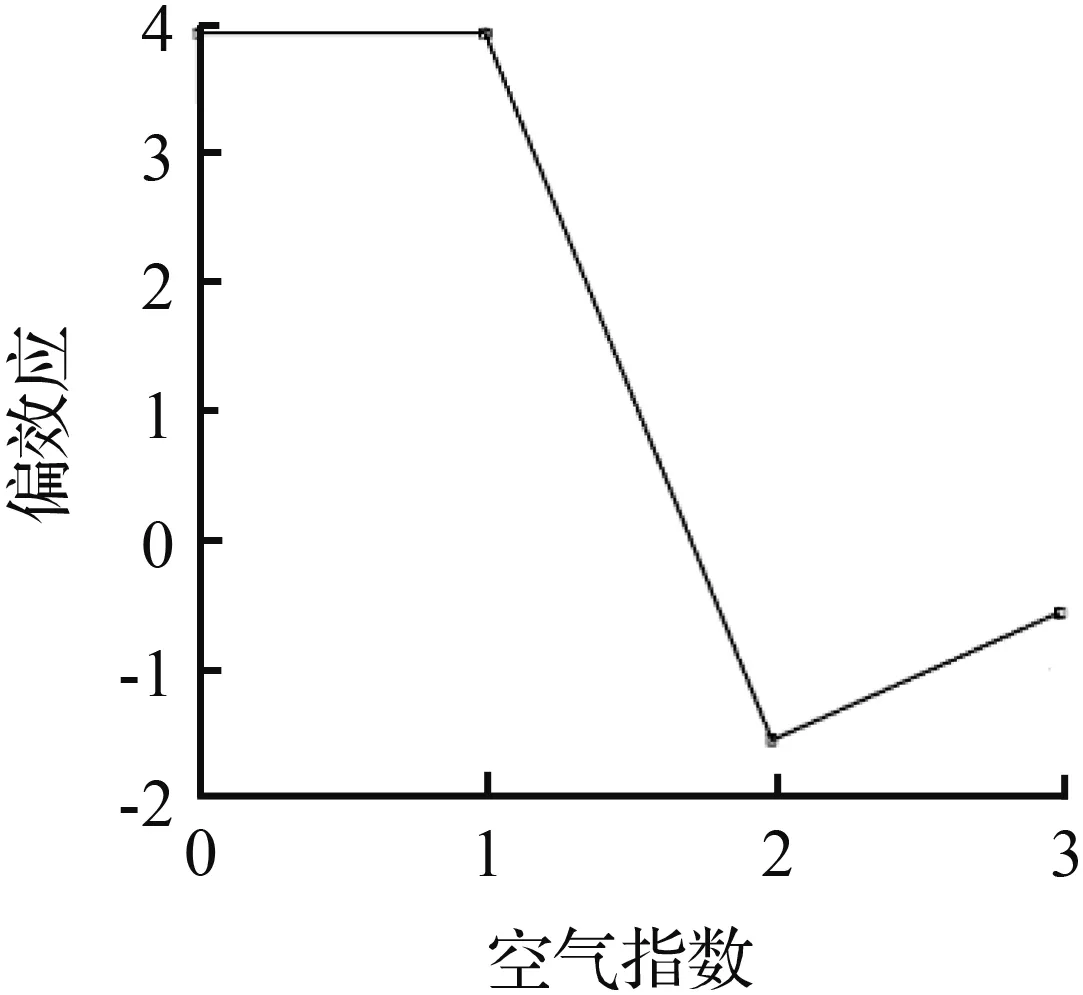
图9 565路几个影响因子的偏效应Fig.9 Partial effect of influence factors on line 565

图8和图9是从104路和565路公交客流数据特征数据集中选取的6个对客流变化影响较为显著的特征标签。

从图8可以看到，特征“一周中第几天”由0变为1、由4转为变为5时偏效应指标都出现了明显的上升，与104路客流周变图中的两个上下班高峰相吻合。而一天中“最高温”由13 ℃升到15 ℃时，偏效应值从15急剧上升到0.19，随着“最高温”一路增加到27 ℃，偏效应也开始缓慢地上升，27 ℃之后偏效应指标随着“最高温”的上升反而呈现下降的趋势，表明对于104路客流15～27 ℃是一个比较适合出行的温度区间，超出这个区间，乘客出行欲望会降低。最低温在4～10 ℃和12～14 ℃偏效应维持较为平稳，在“最低温”在10 ℃和14 ℃处继续升高时偏效应都发生了突变，显示出10～14 ℃的“最低温”范围对乘客是否出行影响较大。当发生下雨和放假的情况时，偏效应都明显降低，说明发生上述事件时乘客的出行会明显减少。“一天中小时”引起的偏效应变化与客流时变图趋势一致，上午8-9时和下午5-6时为偏效应的两个最高点，同时也是客流出行的两个尖峰时段。最后，随着“空气指数”指数从轻度污染变为中度污染，它对预测客流的偏效应开始由3变为-10，显示出“空气指数”指数总体上对客流影响比较轻微，只有空气质量下降到一定程度，公交客流才会受到影响565路在这一点的情况与104路类似。

图9中，“一周中第几天”在值由0变为1和4变为5,即周一上午和周五下午这两个时间点偏效应都发生了明显的正向突变，并且变化的数值区间要低于104路客流状况，可能是因为104路的通勤客流比例要高于565路。随着“最高温”由13 ℃升到31 ℃，偏效应也随着近似线性增大。而“最低温”在4～9 ℃偏效应在4.3附近保持平稳，在最低温升高到10 ℃时偏效应突然下降到-2，随后“最低温”逐渐升高时偏效应的值持续增大到3。出现节假日和下雨两种情况时，565路客流偏效应的变化情况与104路保持一致。此外，“一天中小时”对565路客流的影响与104路相同，都呈现两个驼峰的态势，但是由于104路客流量明显高于565路，104路的“一天中小时”对偏效应的影响在数值上要远远高于565路。

5 结论

本文主要研究了一种基于双层堆叠模型的短时公交客流预测算法。讨论了几种不同的机器学习学习算法在各种情况下的预测性能，对比情况显示了基于stacking的S-Catboost模型在预测精度和稳定性上的优势，说明了S-Catboost模型在公交客流预测领域有着明显的应用前景。

此外，S-Catboost相比于目前其他主流的机器学习算法，更大的优势在于对公交多源特征的挖掘，通过深入探索公交客流波动有关的影响因子与预测目标的关系，极大地提高预测模型的精准性。不同于神经网络的黑箱式拟合过程，S-Catboost对预测结果的可解释性很好同时决策树的决策结果能够对这些影响因子进行重要性排序和偏效应分析。