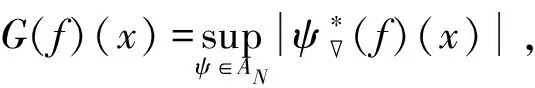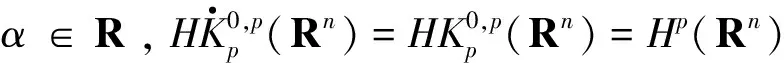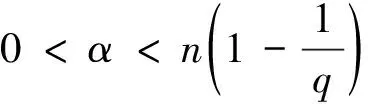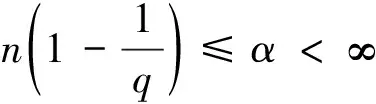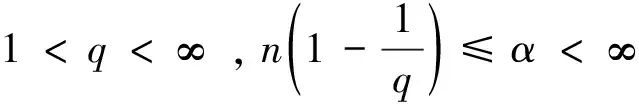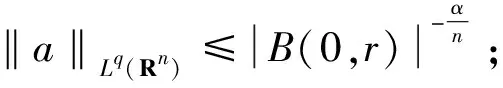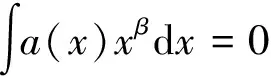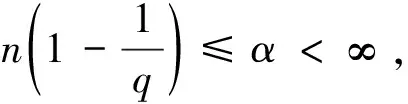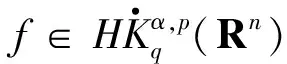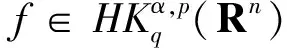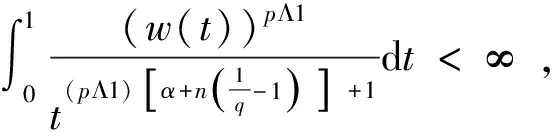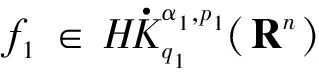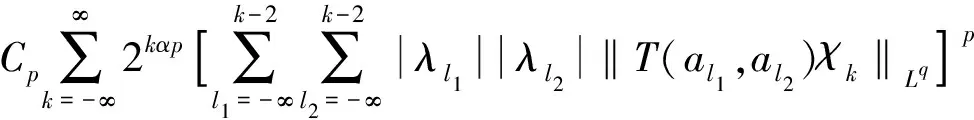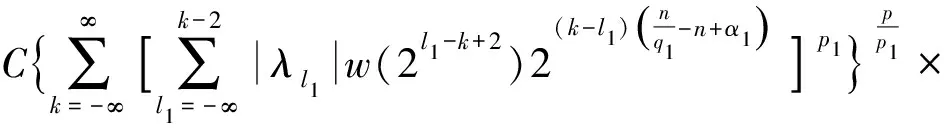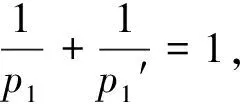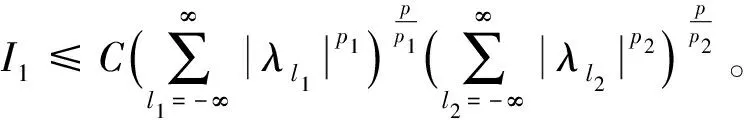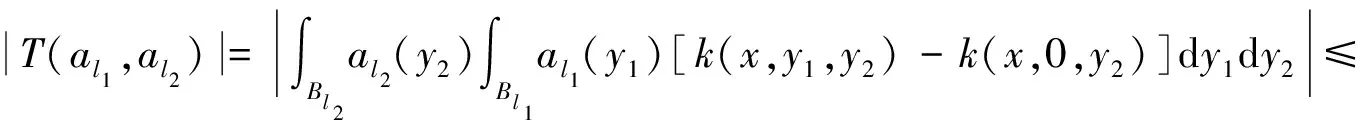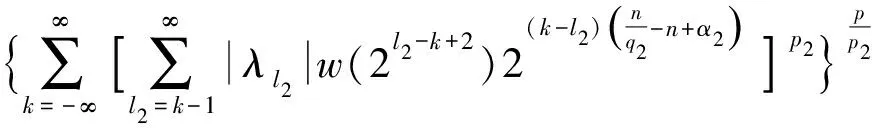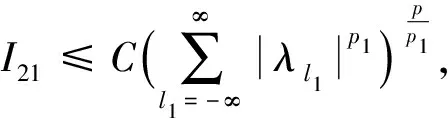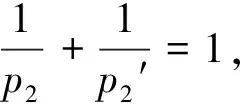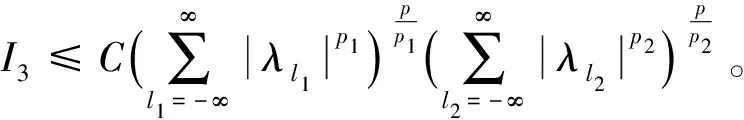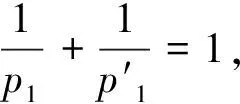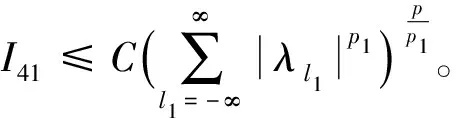Dini型多线性Caldern-Zygmund算子在Herz型Hardy空间上的有界性
王美仲,叶晓峰
(华东交通大学 理学院, 江西 南昌 330013)
0 引言
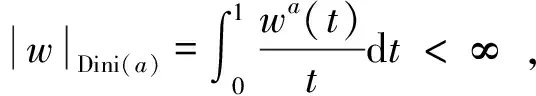
近些年来,多线性算子理论得到了快速发展,Coifman和Meyer首先在文献[1-2]中提出了多线性算子。这一理论的提出使调和分析取得了重要的突破。
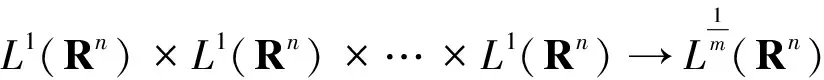
定义1[3]定义在{(Rn)m(x=y1=y2=…=ym)}之外的一个局部可积函数k(x,y1,…,ym)被称为w(t)型m-线性c-z核。如果存在这样一个常数A>0,使得
(1)
且(x,y1,…,ym)∈(Rn)m+1,x≠yj,对于j∈{1,2,…,m},有:
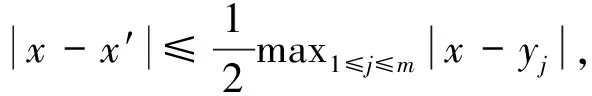
(2)
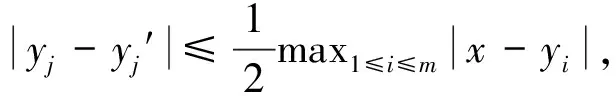
(3)
如果
记T:φ(Rn)×…φ(Rn)→φ′(Rn)是一个具有w(t)型C-Z核的m-线性c-z算子,其φ∈S(Rn),S(Rn)为施瓦兹函数空间。
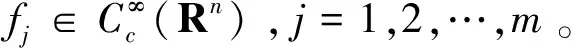
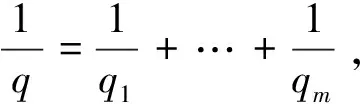
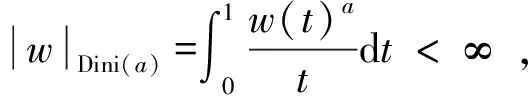
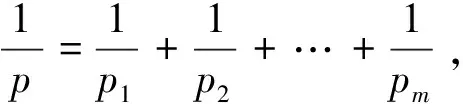
令Bk={x∈Rn:|x|≤2k},Ek=BkBk-1且χk=χEk,w∈Dini(a),k∈Z。其中χE表示集合E的特征函数。
定义3[4]设α∈R且0 (4) 其中 (5) 当p=∞时作相应修改。 其中 (6) 当p=∞时作相应修改。 定义4[4]设α∈R且0 本文只讨论了齐次Herz型Hardy空间的情况,对于非齐次的情况类似,这里省略了非齐次Herz型Hardy空间的讨论。这些空间有下列的关系: 与Hardy空间的理论一样,对Herz型Hardy空间也有很多相关的研究。根据中心原子给出了Herz型Hardy空间的特征分解。 ① 对某个r>0, suppa⊂B(0,r)={x∈Rn:|x|≤r}; ④ 对某个r≥1, suppa⊂B(0,r)。 若a(x)满足①~③,则Rn上函数a(x)称为中心(α、q)原子。 若a(x)满足②~④,则Rn上函数a(x)称为限制型中心(α、q)原子。 (7) 下确界取遍f的所有如上的分解。 (8) 下确界取遍f的所有如上的分解。 定理 为了估计I1,考虑当l1≤k-2,l2≤k-2,x∈Ek,对于l1和l2,设l1≤l2且al1是中心(α1,q1)原子,则 代入I1有 故对于I11,当0 对于I2,因为l1≤k-2,l2≥k-1,且x∈Ek。又因al1是中心(α1,q1)原子,则有 代入I2有 对于I4,由于T是从Lq1(Rn)×Lq2(Rn)到Lq(Rn)有界的,则 =CI41×I42。 对于I41,当0 根据I1,I2,I3,I4,本文有 最后对f1,f2所有的分解取下确界得 对于非齐次Herz型Hardy空间也有上述类似的结论,这里省略了证明。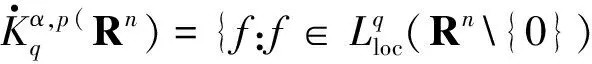
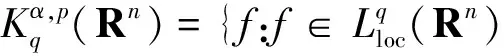
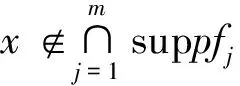
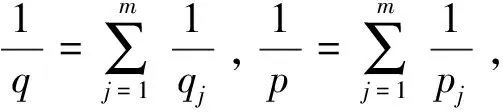
1 乘积Herz型Hardy空间的有界性