双隧道开挖对地表沉降及地埋管线的影响研究
李志南1,潘珂1,王位赢1,唐晓菲5,马少坤2,3,4,段智博2
(1.广州地铁设计研究院股份有限公司, 广东 广州 510010;2.广西大学 土木建筑工程学院, 广西 南宁 530004;3.工程防灾与结构安全教育部重点实验室, 广西 南宁 530004;4.广西防灾减灾与工程安全重点实验室, 广西 南宁 530004;5.广西交通设计集团有限公司, 广西 南宁 530029)
0 引言
随着地铁隧道建设里程的不断增加,地铁隧道布置形式日趋复杂,其中主要表现为双隧道或多线叠交布置。在如此复杂的环境下进行地铁隧道的施工,确保既有隧道及地埋管线的正常使用尤为重要。针对此问题国内外学者开展了大量的离心模型试验和数值分析。崔允亮等[1]针对地下综合管廊上跨拟建地铁隧道的工况,采用光纤监测及数值模拟等手段研究了盾构施工对管廊竖向位移的影响。刘颖彬等[2]以上海地铁14号线盾构下穿地铁6号线双圆隧道为工程背景,对双圆隧道在被下穿前后的变形进行研究。LIN等[3]采用数值模拟的方法,对新建双隧道斜下穿既有隧道的变形进行研究。MA等[4]开展了离心模型试验并与数值分析进行对比,研究了不同开挖顺序双隧道对地表沉降及既有管线的影响。VORSTER 等[5-7]通过三维离心模型试验对不同地层损失率下隧道开挖所致地表位移、管线竖向位移、管线弯矩、管线周围土体应变进行了研究。金大龙等[8]采用离心试验分析了小净距隧道施工对周围土体的影响,结果发现四线隧道在小净距条件下开挖会产生明显的“群洞效应”,使得土体向上扩展并使得新建隧道周边竖向土压力增加。ZHANG等[9]在边界元模型的基础上,提出了基于位移控制的两阶段法预测层状土中既有管道在隧道变形作用下的变形行为,使得隧道开挖所致的土层位移对管道的作用得以量化。魏纲等[10]通过三维有限元分析发现,当管线与隧道平面垂直时,随管线埋深的增大,管线的竖向位移和水平位移呈线性变化,并且随着管-土模量比的增大两者的值减小;随管线刚度增大,管线变形减小。NGOC等[11]采用应力控制有限元法分析了双隧道施工对地表沉降的影响,发现双隧道开挖形成的地表沉降槽具有不对称性。上述对隧道开挖引起地层变形的研究均未考虑先行隧道的对土体和管线影响机理。先行隧道盾构施工时,地层受到一定程度的扰动并达到新的平衡,后行隧道的开挖条件将与先行隧道相比更加复杂,对地层及周边构筑物的影响也将有更多不确定性。双线隧道施工时,后施工的隧道可能会影响先施工隧道使地表土体产生更大沉降;当后行隧道位于先行隧道下方时,新建隧道上方先行隧道的存在会制约地层位移场的演化;当后行隧道位于先行隧道上方时,后行上部隧道开挖可能减缓土体的沉降趋势。因此,针对不同布置形式的双隧道在不同施工顺序下开挖导致的地层变形特点进行研究很有必要。
本文以数值模拟为主要研究手段,首先通过与文献[4]中的离心模型试验结果对比验证其有效性,然后考虑双隧道不同垂直距离、不同开挖顺序等工况进行数值模拟分析,着重研究地表沉降、管线沉降、土体剪应变和土体主应力的变化规律,从而系统地研究了双隧道开挖对地表沉降和临近管线的作用机理及影响效果。
1 双隧道开挖对地埋管线影响的数值模拟方案
1.1 数值模拟方案

图1 断面布置图Fig.1 Section layout of the numerical analysis
采用三维有限元分析方法对竖向平行双隧道开挖所致地表沉降及管线变形的影响规律和作用机理进行分析,从而得到双隧道不同开挖顺序及垂直间距条件下开挖所致的隧道—管—土之间的相互作用规律。图1所示为双隧道与管线的相对位置,图1中S为双隧道圆心距离;DT为隧道外径,H为双隧道圆心垂直距离;S1为下部隧道圆心至地表距离;S2为上部隧道圆心至地表距离;S3为管线顶部距地表距离。当上下两个隧道在水平方向上有间距时,为肩驮式(P)布置;当上下两个隧道在水平方向完全重合,即S=0时,为重叠式(S)布置。主要考虑肩驮式双隧道的不同开挖顺序及垂直间距条件的影响,因此分别设计了先上后下(PUL1~PUL8)和先下后上(PLU1~PLU8)各8组不同垂直间距的数值模拟。同时,为了验证数值模拟的准确性,设置了2组对照试验,PUL与SUL(PUL:肩驮式先上后下,SUL:重叠式先上后下),与文献[4]中的离心模型试验结果对比。U和L分别代表上部隧道和下部隧道。例如PUL代表先开挖上部隧道后开挖下部隧道。相关数值模拟方案见表1。
1.2 土体本构模型及参数选取
选取一种改进的亚塑性模型(HP模型),该模型可合理地反应土体的非线性小应变的特性,最初由WOLFFERSDORFF[12]提出,NIEMUNIS等[13]引入了5个参数使其更好地反映土体的小应变特性,土体的所有参数及取值见表2。
1.3 隧道开挖模拟方法
采用位移控制有限元法模拟隧道开挖过程,可以准确的模拟任意地层损失比。地层损失率已知的情况下隧道开挖断面收缩所致的间隙系数g0可通过式(1)求出。
(1)
式中,RT为隧道半径;ε0为地层损失率。

图2 隧道截面位移边界条件Fig.2 Displacement boundary on tunnel section
PARK[14]在总结大量数据之后提出隧道开挖截面的收缩模式如图2所示,其位移表达式如下:
(2)
(3)

编写ABAQUS有限元子程序,通过对隧道施加位移边界条件,从而可模拟隧道开挖所导致地层损失,地层损失率同模型试验为2%的地层损失。隧道开挖模拟采用“wished-in-place”方式激活管线,即不考虑管线施工过程的影响。设计单个隧道分6段开挖完成,限制预开挖隧道段前方掌子面的水平位移并杀死预开挖隧道段内的土体,同时调用ABAQUS子程序在隧道表面施加位移边界条件,即完成一段隧道的开挖,每段隧道开挖3.6 m,重复上述步骤至双隧道开挖完成。

表1 数值模拟方案Tab.1 Numerical simulation scheme

表2 HP模型参数Tab.2 The parameters of HP model
1.4 数值模型建立
参照文献[19]的离心试验参数以及南宁地铁1号、2号线为依托,建立数值模型,模型尺寸与离心试验所对应的原型尺寸相同,即宽60.000 m、高45.000 m,隧道外径6.000 m,管线外径1.905 m。为了充分消除边界条件的影响,模型长度设为120.000 m。图3为PUL1方案的模型图。根据目前市政工程中主管线广泛采用的尺寸和材料,按比例设定管线相关参数见表3。管线材料采用6016型铝管制成。土体与管线之间的相互作用采用Coulomb摩擦理论,摩擦系数为0.513,最大弹性滑移的限制位移为5 mm。管线与土体均采用三维八节点六面体单元(C3D8)。
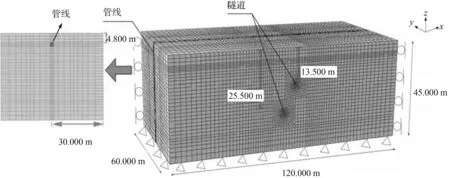
图3 数值模型Fig.3 Numerical model

表3 管线相关参数Tab.3 Parameters of pipeline model

2 数值模拟验证
为了验证数值模拟的有效性,首先将计算结果与文献[20]的离心模型试验进行对比,离心加速度60 g。图4所示为离心试验的布置图,第一组为肩驮式(隧道轮廓为实线),第二组为重叠式(隧道轮廓为虚线)。开挖工序为先开挖上部隧道后开挖下部隧道。模型管由6016型铝管制成,外径31.75 mm,厚度2.08 mm,长度1 150.00 mm,分别对应实际工况中的1.905、0.125、69.000 m。模型隧道由铝材制成,直径100.00 mm,厚度3.00 mm,内外套有硅酮橡胶膜,试验准备阶段在内膜和外膜中注入与土体密度相同的ZnCl2重液,在试验过程中放出内膜重液模拟隧道开挖所致重力损失,同时放出外膜重液模拟开挖所致地层损失,模型隧道如图5所示。具体试验过程及步骤详见文献[4]。
离心试验与数值模拟结果如图6所示。从图6中可以看出,对于PUL工况,先开挖上部隧道再开挖下部隧道,数值拟合值与试验测量值吻合较好,二者呈现出的规律相同,证明了采用的数值模拟是准确的。对于肩驮式双隧道,对比不同开挖顺序2种工况下开挖完成后所致地表沉降最大值,先下后上比先上后下大12%;而对于重叠式双隧道,对比2种工况下双隧道开挖完成后所致地表沉降最大值,先上后下比先下后上大18%。肩驮式双隧道与重叠式双隧道两种布置形式时,先开挖上部隧道再开挖下部隧道与先开挖下部隧道再开挖上部隧道两种开挖形式所致地表沉降大小刚好相反。这是因为不同开挖顺序及不同双隧道叠合形式造成不同程度的遮拦效应,进而引起上述地表沉降的差异。

图4 离心试验断面布置图Fig.4 Centrifugal test layout

图5 隧道模型图Fig.5 Tunnel model

(a) 肩驮式双隧道

(b) 重叠式双隧道

图7 双隧道开挖所致最大地表沉降与双隧道垂直间距关系Fig.7 Relationship between the vertical spacing and the maximum ground settlement caused
3 不同垂直间距肩驮式双隧道开挖数值模拟结果分析
3.1 对地表沉降的影响
图7为不同开挖顺序时双隧道开挖所致最大地表沉降与双隧道垂直间距关系。对于肩驮式双隧道,先上后下开挖时,双隧道垂直间距为1.0DT时,地表沉降最大值为75 mm,随双隧道垂直间距增大,双隧道开挖后最大地表沉降迅速减小,双隧道垂直间距大于2.0DT时逐渐稳定。先下后上开挖时,随双隧道垂直间距增大,双隧道开挖后最大地表沉降平稳减小。由此可得,先下后上开挖时,地表沉降对于双隧道垂直间距的响应不如下上后下开挖时敏感。以2.0DT为界,当双隧道垂直间距小于此值时,先上后下产生的地表沉降明显大于先下后上,当双隧道垂直间距大于此值时,两种开挖顺序的导致的地表沉降相差不大。
3.2 对管线变形的影响
不同垂直间距双隧道开挖所致管线竖向应变如图8所示。图8(a)为先上后下工序下开挖时不同垂直间距的双隧道开挖所致管线竖向应变图,正值为受拉区域,负值为受压区域。从数值上来看,当双隧道垂直间距为1.0DT和1.5DT时,双隧道开挖所致管线的竖向应变较大,分别为254和234微应变,至2.0DT时管线竖向应变为146微应变,减小幅度为38%。当双隧道垂直间距大于2.0DT时,随垂直间距增大,管线的竖向应变减小,但减小幅度较小,约为14%。从管线受拉区宽度来看,双隧道垂直间距小于2.0DT时,受拉区范围约为-1.0DT~2.6DT,双隧道垂直间距大于2.0DT时,受拉区范围约为-1.8DT~2.8DT,受拉区宽度增大,因此管线受双隧道开挖影响的范围与双隧道垂直间距有关,垂直间距越大,管线受开挖影响的范围越大。图8(b)为先下后上工序下开挖时不同垂直间距双隧道开挖所致管线竖向应变图。整体来看,管线竖向应变在垂直间距为1.0DT时最大值为176微应变,这个值随双隧道垂直间距的增大而减小,但减小幅度并不大,双隧道垂直间距为2.0DT时,管线沉降减小了8%,管线最大竖向应变减小了12%;当双隧道垂直间距为2.0DT~3.0DT时,管线沉降减小了6%,管线最大竖向应变减小了10%。并且,双隧道垂直间距增大的同时,上部隧道与管线的距离也越来越近,但是管线最大沉降位置并没有明显改变,说明在先行下部隧道扰动效应下,后行上部隧道对管线的影响较小,并且扰动效应的强度并没有明显的变化。总体上,先上后下在双隧道垂直间距小于2.0DT时产生的管线竖向应变较大。

(a) 先上后下

(b) 先下后上

图8 不同垂直间距双隧道开挖所致管线竖向应变Fig.8 Vertical strain of pipeline caused by twin tunnels excavation at different vertical spacing
3.3 管—土—隧相互作用
为进一步探究管—土—隧的相互作用机理,选取肩驮式双隧道不同开挖顺序时典型工况的土体主应力分布如图9、图10所示。图9、图10中小“十字”的纵向长边代表第一主应力大小,横向短边代表第三主应力大小,“十字”的旋转代表主应力轴的旋转。先上后下开挖时,两隧道间的土体受到后行下部隧道开挖影响,为了维持平衡,土体的抗剪强度发挥作用,土单元的主应力轴旋转,并将应力向四周传递。如图9(a)所示,当双隧道垂直间距较小(1.0DT)时,先行上部隧道顶部及底部土体的主应力轴均随着后行下部隧道的开挖而发生明显改变,说明此时先行上部隧道的遮拦效应较弱,后行下部隧道的二次扰动更强。如图9(b)所示,当双隧道垂直间距增大(3.0DT)时,先行上部隧道顶部土体主应力大小及方向变化程度小于其底部土体的变化程度,此时先行上部隧道的遮拦效应有所增强。图10是先下后上工序下开挖后土体的主应力分布(部分典型工况),与图9揭示了类似的规律,说明土体的主应力分布变化与双隧道开挖顺序关系不大。

(a) H=1.0DT

(b) H=3.0DT

(a) H=1.0DT

(b) H=3.0DT
图11与图12所示为不同开挖顺序时双隧道开挖后的土体剪应变分布图(部分典型工况)。土体剪应变分布情况体现了隧道开挖对土体造成的扰动,剪应变越大,则开挖对土体造成的扰动越大,其直观反映为地表沉降及管线沉降。对于肩驮式双隧道,双隧道处于相切位置,上下隧道之间的土体剪应变重合,无论是先上后下还是先下后上的开挖顺序,先行隧道对后继开挖隧道存在遮拦效应影响,后继开挖隧道处于隧道的主要影响区内;当双隧道之间垂直间距为3.0DT时,两隧道之间的剪应变与水平向呈45°形成一条稀疏带,此时可认为双隧道之间扰动效应基本消失。对比图11与图12,当双隧道垂直间距为1.0DT时,图12(a)土体剪应变小于图11(a)剪应变数值,产生剪应变的土体范围大于图11(a)中的范围。然而,双隧道垂直间距为3.0DT时,图12(b)双隧道之间土体剪应变却大于图11(b)剪应变数值。由此可得,先下后上开挖时,双隧道施工对周围土体的影响不如先上后下开挖时剧烈,由隧道开挖导致的土体附加应力应力分布的较为分散。这也解释了为何相较于先上后下,先下后上开挖时后行上部隧道对管线的影响较小,同时产生较小的地表沉降。

(a) H=1.0 DT

(b) H=3.0 DT
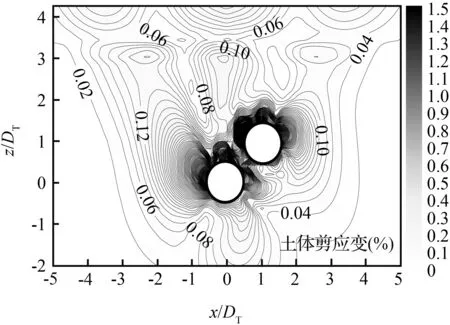
(a) H=1.0 DT

(b) H=3.0 DT
4 结论
① 对于肩驮式双隧道,开挖顺序对管线及地表沉降的影响显著。先开挖上部隧道时,会产生较大的管线变形和地表沉降。
② 随着双隧道垂直间距的增大,地表沉降和管线变形减小,但管线和周围土层受开挖影响的范围增大。当双隧道之间的垂直间距大于3.0DT时,双隧道之间的相互扰动效应基本消失。
③ 建议双隧道垂直间距小于2.0DT时采用先下后上的开挖顺序,双隧道垂直间距大于3.0DT时采用先上后下的开挖顺序。
④ 现实工程中盾构双隧道开挖时,应综合考虑双隧道间的扰动效应及遮拦效应的影响,不应仅仅的采用叠加法进行隧道设计和施工。

